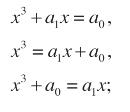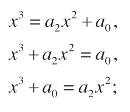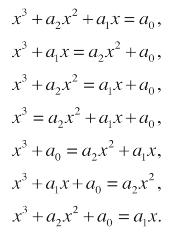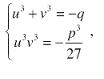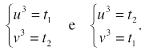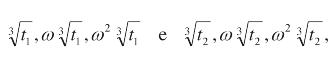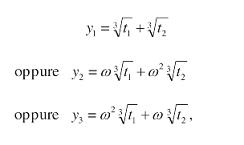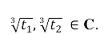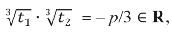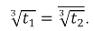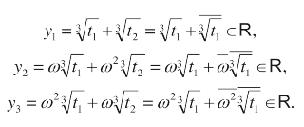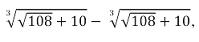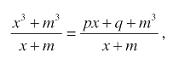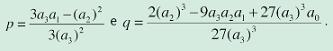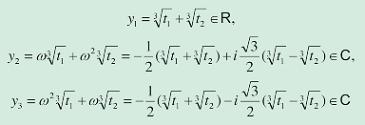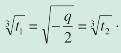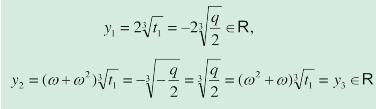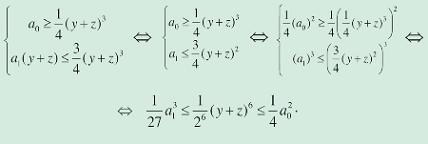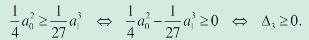Cardano e le equazioni di terzo grado

L’importanza del ruolo di Cardano nella risoluzione delle equazioni di terzo grado è ben nota. In questo scritto cercheremo di fornire una visione articolata, per quanto compatta, della strategia di Cardano nell’affrontare la questione.

Riproporremo quindi dapprima una breve biografia di Cardano e accenneremo alla disputa con Tartaglia sulla priorità della scoperta delle formule risolutive, per inquadrare il problema da un punto di vista storico. In seguito, dopo aver richiamato l’attuale risoluzione delle equazioni di terzo grado, vedremo nel dettaglio come Cardano arrivi alla soluzione e quali problemi essa comporti.

Infine, cercheremo di ricostruire il contesto delle altre opere in cui Cardano tratta delle equazioni di terzo grado con particolare attenzione a un’opera ancora poco nota, il De Regula Aliza.

1. Girolamo Cardano

2. Cardano e la Matematica

3. Il problema delle equazioni di terzo grado e l'Ars Magna

4. Il metodo risolutivo

5. Le altre Opere

6. De Regula Aliza

7. Il metodo di Cardano 

1. Cardano (Pavia 1501 - Roma 1576) fu medico di fama internazionale e matematico. Si guadagnò da vivere esercitando la professione medica, insegnando Matematica a Milano e Medicina a Pavia e Bologna. Non è ricordato per il suo buon carattere e non ebbe una vita particolarmente fortunata, anche in termini economici. Qualche anno dopo la condanna a morte nel 1560 del figlio prediletto, Cardano si vide costretto a denunciare l’altro suo figlio che lo diffamava e che giunse a derubarlo.

Nell’ottobre del 1570 Cardano venne arrestato dal tribunale dell’Inquisizione, forse per alcuni aspetti poco ortodossi delle sue opere (tra i quali un oroscopo di Gesù Cristo) o forse per la sua vicinanza ad ambienti protestanti. Quattro mesi dopo si sottomise all’abiura che gli venne imposta e, in una lettera al pontefice, si impegnò a non tenere più lezioni pubbliche né a pubblicare altre opere. Gli ultimi anni della sua vita, sotto la protezione papale a Roma, vennero dedicati alla stesura della sua autobiografia.

La produzione di Cardano è sterminata: nel 1663 il medico Charles Spon curò a Lione l’edizione delle sue opere, in dieci tomi, che spaziano tra Filosofia, Medicina, Meccanica, Matematica, Astrologia. Si ricordano inoltre decine di manoscritti.

Di Cardano matematico ci sono pervenute dodici opere a stampa, tutte raccolte (non necessariamente in ordine cronologico) nel quarto tomo dell’Opera Omnia, tranne una nel decimo. Quelle più note sono l’Artis Magnæ sive De Regulis algebraicis (1545, 1570 e 1663, meglio nota come Ars Magna), l’ArsMagna Arithmeticæ (1663 postuma, composta probabilmente tra il 1539 e il 1542, si veda in bibliografia[ 13]) e la Practica Arithmeticæ (1539, 1663). A queste affiancheremo il De Regula Aliza (1570, 1663) che si inserisce in un dialogo organico con i tre testi citati per comunanza di argomenti.

2. In campo matematico, Cardano divenne celebre per aver trovato le formule risolutive per le equazioni di terzo grado che appaiono per la prima volta nell’Ars Magna del 1545. Tuttavia, la paternità delle formule è controversa. Infatti già tra il 1505 e il 1515 Scipione del Ferro, professore di Aritmetica e Geometria a Bologna, scopre le formule risolutive per alcune equazioni cubiche (quelle prive del termine di secondo grado) ma tiene il risultato segreto fino a poco prima della sua morte, quando lo confida al suo allievo Antonio Fiore. Spinto dalle voci che cominciavano a circolare, Niccolò Tartaglia si interessa alla questione e riesce a risolvere due dei tre tipi di equazioni cubiche prive del termine di primo grado (x³ + a2x² = a0 e x³ + a0 = a2x²).

Nel 1535, in seguito alla sfida lanciata da Antonio Fiore, Tartaglia risolve anche l’equazione x3 + a1x = a0 e, dopo qualche giorno, le altre equazioni cubiche prive del termine di secondo grado (x³ = a1x + a0 e x³ + a0 = a1x). La notizia raggiunge a Milano Cardano, che era in procinto di pubblicare la Practica Arithmeticæ. Dopo una lunga opera di persuasione e a condizione di non pubblicare i risultati prima di Tartaglia stesso, Cardano convince quest’ultimo a rivelargli il segreto delle sue soluzioni.

Nel 1539 Tartaglia invia in versi a Cardano le tre regole per le equazioni cubiche prive del termine di secondo grado. Pochi mesi dopo, Cardano scrive a Tartaglia chiedendo spiegazioni a proposito del cosiddetto caso irriducibile, senza ricevere risposta.

Cardano tuttavia non mantiene la propria promessa. Nel 1545 pubblica l’Ars Magna, dove compaiono le formule risolutive per le equazioni di terzo grado prive del termine di secondo grado (quelle trovate appunto da Tartaglia), a cui viene aggiunta per ciascuna una dimostrazione e dove inoltre compaiono le formule per tutte le altre equazioni di terzo grado e anche per quelle di quarto grado, grazie all’allievo Ferrari. Cardano riconosce che Tartaglia gli aveva confidato alcune formule. Tuttavia argomenta che, da un lato, è il primo a fornire le dimostrazioni delle formule e, dall’altro, contesta a Tartaglia proprio la priorità della scoperta delle formule [nota 1]. Infatti, nel 1542 Cardano e Ferrari avevano rinvenuto a casa di Annibale della Nave la soluzione del suocero Scipione, di cui Tartaglia pare non fosse a conoscenza.

In seguito alla pubblicazione dell’Ars Magna, Tartaglia pubblica in tutta fretta nel 1546 i Quesiti e inventioni diverse per rivendicare la propria scoperta. Nel 1547 Ferrari, in qualità di difensore di Cardano, attacca Tartaglia con il primo di dodici Cartelli, che terranno impegnati i due per circa un anno e mezzo, al termine del quale si incontreranno a Milano per sfidarsi pubblicamente [nota 2] .

3. Per Cardano e i suoi contemporanei il problema non riguarda la risoluzione di una singola equazione generale di terzo grado, bensì la risoluzione di tredici equazioni nelle quali sono imposte ulteriori condizioni sui coefficienti. In termini moderni [nota 3], si ammettono solo coefficienti razionali positivi non nulli. Cardano infatti dedica un capitolo dell’Ars Magna a ciascuna delle seguenti equazioni di terzo grado [nota 4]:

• prive del termine di secondo grado:

• prive del termine di primo grado:

• complete:

Queste esauriscono tutte le possibilità [nota 5]. Di queste equazioni, Cardano cerca le soluzioni positive, dette “vere”.

4. Ricordiamol’attuale metodo risolutivo [nota 6], strettamente imparentato con il procedimento di Cardano. Data l’equazione completa:

(1) a3x³ + a2x² + a1x + a0 = 0,

dove a3, a2, a1, a0 appartengono a C e a3 ≠ 0, cerchiamo le soluzioni in C. Grazie alla sostituzione x = y - a2/3a3, possiamo sempre ridurci a un’equazione in cui il coefficiente del termine di terzo grado sia unitario e che sia priva del termine di secondo grado:

(2) y³ + py + q = 0,

dove [nota 7] p, q appartengono a C.

Introduciamo due nuove variabili u, v tali che y = u + v. Sostituendo in (2), otteniamo:

(3) u³ + v³ + (3uv + p)(u + v) + q = 0.

Osserviamo che possiamo imporre su u, v arbitrarie una seconda condizione, ad esempio quella suggerita dall’equazione precedente [nota 8] 3uv + p = 0. In questo modo, l’equazione (3) diventa più semplice:

(4) u³ + v³ + q = 0.

Allora, se si sa risolvere il sistema (5) che proviene dalle due condizioni su u, v:

si sa risolvere anche (1).

Osserviamo che il sistema ha diciotto soluzioni in u, v e due soluzioni in u³, v³. Siamo interessati alla somma u + v che ci deve dare le tre soluzioni per l’equazione di terzo grado (2), quindi per (1). Consideriamo come incognite u³, v³. Il sistema (5) è allora associabile all’equazione:

(6) t² + qt - p³/27 = 0

Ora, usando la formula risolutiva per le equazioni di secondo grado, ricaviamo a cascata le soluzioni delle altre equazioni. Troviamo quindi le due soluzioni t1, t2 per l’equazione (6), da cui ricaviamo le due soluzioni del sistema (5):

Consideriamo la prima soluzione. Vogliamo trovare u, v.

Le radici cubiche di t1, t2 in C hanno tre determinazioni ciascuna:

dove w è una radice cubica primitiva dell’unità [nota 9]. Ci sono quindi nove combinazioni possibili per u + v. Fatta una scelta per u, sappiamo che deve valere la condizione 3uv + p = 0, vale a dire uv = - p/3. Si verifica che solo tre combinazioni la soddisfano, da cui:

che sono le tre soluzioni di (2). Considerando poi la seconda soluzione del sistema (5), dove i valori per u3, v3 sono scambiati, troveremo gli stessi valori per l’espressione simmetrica u + v. Quindi, le soluzioni di (1) sono xi = yi - a2/3a3 per i = 1, 2, 3, vale a dire scritte in forma esplicita:

Chiamiamo Δ3 = q²/4 + p³/27 il discriminante dell’equazione di terzo grado. Osserviamo che per il terzo grado, a differenza del metodo risolutivo per le equazioni di secondo grado, l’interpretazione geometrica del completamento del cubo non aiuta a chiarire intuitivamente né l’espediente algebrico dell’introduzione delle due nuove variabili u, v, né la riduzione del numero delle soluzioni del sistema ausiliario (5). Osserviamo inoltre che, se a3, a2, a1, a1 appartengono a R e quindi p, q appartengono a R, è possibile discutere la natura delle soluzioni di (5) a partire dal segno del discriminante D3. Sappiamo che ogni equazione a coefficienti reali di grado dispari ha almeno una soluzione reale, come conseguenza del teorema del valore medio. Nel caso Δ3 > 0, abbiamo una soluzione reale e due soluzioni complesse coniugate [nota 10]. Nel caso Δ3 = 0, abbiamo tre soluzioni reali, di cui due coincidenti [nota 11]. Infine, sia Δ3 < 0: allora abbiamo tre soluzioni reali distinte. Infatti,

Inoltre, poiché:

e sono coniugati:

Quindi:

Quest’ultimo caso è chiamato irriducibile: Δ3 < 0 significa che nella formula risolutiva compaiono dei numeri immaginari puri e si può dimostrare che in questo caso essi devono comparire necessariamente (si veda ad esempio in bibliografia [21], [1], [20], [15] e [16]). È proprio questo punto della risoluzione che costituiva un problema di una certa rilevanza per Cardano e i suoi contemporanei.

Inoltre, conseguenza inevitabile di questo metodo è che la risoluzione di un’equazione di terzo grado viene ridotta al calcolo di radici cubiche, che non sempre è facile da portare a termine. L’espressione della soluzione quindi può essere talvolta complicata. Ad esempio (si veda in bibliografia [7, cap. XI]), l’equazione x³ + 6x = 20 ha come unica soluzione reale 2, ma la formula restituisce:

che appunto [nota 12] è:

5. È interessante esaminare il contesto costituito dalle altre opere di Cardano, che permette di giungere alla scoperta del problema posto dal caso irriducibile e di come egli cerchi di rimediarvi.

Fino alla fine degli anni ’30 del XVI secolo, Cardano sapeva risolvere tramite artifici solo alcuni tipi di equazioni di terzo grado particolari. Testimone ne è la Practica Arithmeticæ, pubblicata appunto nel 1539. È un testo di Matematica pratica, che rimane ancora in ambito abachistico e in cui le equazioni ricoprono soltanto il ruolo di strumenti e non di oggetto di indagine (si veda in bibliografia [14]). Nessun cenno è fatto all’esistenza di formule risolutive per equazioni non particolari.

Un testo invece più pertinente è l’Ars Magna Arithmeticæ, pubblicata per la prima volta nell’Opera Omnia del 1663. Secondo una recente ipotesi di Veronica Gavagna (bibliografia [13]) fu molto probabilmente composta tra il 1539 e il 1542, nel lasso di tempo cioè che intercorre tra la pubblicazione della Practica Arithmeticæ e la scoperta da parte di Cardano e Ferrari dei contributi di Scipione del Ferro.

Il testo nasce inizialmente come supplemento alla Practica Arithmeticæ, ma non viene dato alle stampe, forse proprio a causa del problema rappresentato dal caso irriducibile e forse anche per la concorrenza di un’altra opera in progetto, l’Opus Arithmeticæ Perfectum, di cui tratteremo più avanti [nota 13].

Vale la pena osservare che, tra le regole particolari presenti nell’Ars Magna Arithmeticæ, ce n’è almeno una che Cardano potrebbe usare [nota 14] come strada alternativa al problema posto dal caso irriducibile. Infatti [nota 15], trovata indipendentemente una soluzione x = -m di una certa equazione x³ = a1x + a0, possiamo aggiungere m³ ad entrambi i membri di modo che, dividendo per x + m, si trovi un’equazione di secondo grado:

vale a dire x² - mx + m² = p + (-pm + q + m3) e quindi x² -mx + m² = p. Le altre due radici reali dell’equazione di terzo grado si ottengono poi risolvendo l’equazione di secondo grado.

6. Accenniamo infine a un ultimo testo matematico in cui Cardano tratta della risoluzione delle equazioni di terzo grado. Il De Regula Aliza esce a stampa nel 1570, insieme al De Proportionibus e alla seconda edizione dell’Ars Magna.

Il suo contenuto è finora ancora poco conosciuto, a causa di alcuni problemi di cui soffre. Leggiamo in proposito l’opinione del principale dei suoi lettori, Pietro Cossali (1748- 1815):

“Alla tenebria di quel libro a noi cagionata dalla diversità del linguaggio se ne accoppia un’altra prodotta da un’infinita perversissima folla di errori, e di numeri ne’ calcoli e di lettere sì nelle figure, sì nelle relative dimostrazioni; e bisogna eziandio aggiungersene altra assoluta, ed intrinseca proveniente da mancanza di ordine, per la quale riesce cosa faticosissima e malegevolissima l’unire le fila, vedere il risultato, valutare il discoprimento. Si scorge Cardano, che tenta, che si apre nuove strade, che ritorna sulle battute, che si volge or da un lato, or dall’altro seguendo i suggerimenti varij dell’ingegno; in una parola il libro è l’atto del tentare, non un ordine delle scoperte; e finalmente è un libro di Cardano, che da Bombelli pur suo coetaneo fu denominato nel dire oscuro”[nota 16].

L’Aliza infatti è scritta in un latino a dir poco faticoso, mostra numerosi errori di copiatura e di calcolo ma il vero scoglio sono i contenuti del testo, che non presentano un ordine argomentativo chiaramente riconoscibile. L’ipotesi più plausibile è che Cardano, immediatamente prima dell’abiura del 1571, si sia affrettato a rimaneggiare (almeno parzialmente) e a pubblicare gli scritti e appunti di una vita riguardo al problema che ancora rimaneva aperto sulla risoluzione delle equazioni di terzo grado. L’interpretazione dell’Aliza come testo riguardante il caso irriducibile è dapprima confermata dall’origine della parola “aliza” [nota 17].

Questo termine non è d’uso corrente nella Matematica dell’epoca e non trova altro riscontro nelle opere di Cardano se non nel titolo di questo testo e in qualche riferimento sparso a una certa “regola aliza”.

Inoltre, troviamo un riscontro molto più consistente dell’ipotesi dell’Aliza come testo riguardante il caso irriducibile proprio nel primo paragrafo del capitolo I che, in mancanza dell’introduzione, fa le veci di una sorta di dichiarazione d’intenti:

“Dal momento che nell’Arte Magna abbiamo già dimostrato che tutti i capitoli sono convertiti, sebbene i due principali furono scoperti come generali e non già per conversione, trovato un altro capitolo generale, tranne i capitoli del cubo e delle cose uguali a un numero e del cubo uguale a dei quadrati e a un numero, il quale si deduca per conversione dal precedente, pur essendo generale, è manifesto che tutti i capitoli di tre o quattro termini non solo sono conosciuti nella generalità, ma anche dimostrati, purché questo stesso sia stato trovato con una dimostrazione”.

Una strategia ipotizzata da Cardano per evitare il problema posto dal caso irriducibile sarebbe di ridurre quindi tutte le equazioni a una sola per mezzo di sostituzioni, come abbiamo già visto che egli sa fare nell’Ars Magna, e dare per quest’ultima una formula risolutiva che non ricada nel caso irriducibile e che quindi garantisca la generalità delle risoluzioni già enunciate nell’Ars Magna. La citazione tuttavia presenta passaggi di notevole oscurità. Assumiamo il significato di generale come contrapposto a particolare, vale a dire valido senza condizioni sui coefficienti. L’ipotesi più credibile, ma ancora non del tutto completa, è che Cardano voglia ridurre la risoluzione di tutte le equazioni di terzo grado a quella di x³ = a1x + a0. Infatti, lo studio di questa equazione costituisce non solo il fulcro del resto del capitolo I ma ritorna anche in svariati altri capitoli (bibliografia [6, cap. I, II, III, V, VII, XV, XXV, XXVIII, XL, XLIII, XLVI, XLVIII, XLIX, L, LIII e LVIII]).

In particolare, è peculiare all’Aliza la riflessione sulla sostituzione x = y + z, già usata nell’Ars Magna. Cardano spiega [nota 18] che, sostituendo x = y + z nell’equazione x³ = a1x + a0, si trova:

y³ + 3y²z + 3yz² + z³ = a1(y + z) + a0.

La sua strategia consiste allora nello spezzare il membro di sinistra y3 + 3y2z + 3yz2 + z3 in due parti, da uguagliare alle due parti a1(y + z) e a0 del membro di destra. Tra le 62 possibilità, Cardano sceglie i sette “spezzamenti” [nota 19] “ più facili”, accompagnati talvolta da condizioni:

Le condizioni sono originate da vincoli geometrici [nota 20], se si considera x come il lato di un cubo. Notiamo [nota 21] però che solo la prima condizione implica una condizione sul discriminante Δ3. Nulla è detto da Cardano su come abbia avuto l’idea di usare la sostituzione x = y + z. Tuttavia, nell’Aliza troviamo alcuni capitoli (bibliografia [6, capp. I, V, X, XI, XIII, XVI e LVIII]) che richiamano le riflessioni dell’Ars Magna Arithmeticæ sulla forma che una soluzione può assumere, anche se questa volta limitatamente all’equazione x³ = a1x + a0. Nonostante la trattazione sia meno sistematica, essa è più completa: Cardano precisa ad esempio (bibliografia [6, cap. X]) che la soluzione, nel caso non sia della forma x = r appartenenete a R, deve essere formata da due parti non commensurabili tra loro (si veda in bibliografia [6, capp. V, X, XI, XIII, XVI, LVIII]). Nell’Aliza, per escludere le altre possibilità, considera nel dettaglio non solo i binomi, ma anche i trinomi e i quadrinomi (bibliografia [6, capp. V, X, XI, XIII, XVI, LVIII]). Rimandiamo per i dettagli a un’ulteriore e più dettagliata analisi a venire.

L’Aliza può quindi essere a ragione considerato come un testo che mira a risolvere il problema di generalità posto dalla scoperta del caso irriducibile per le equazioni di terzo grado. Anticipiamo che solo nel corso del XIX secolo sarà dimostrata l’impossibilità di evitare i numeri immaginari puri nel caso in cui un’equazione di terzo grado abbia tre radici reali distinte (si veda in bibliografia [21], [1], [20], [15] e [16]). Disponiamo però di alcune evidenze che potrebbero testimoniare della speranza di Cardano di poter evitare il caso irriducibile.

Infatti è Cardano stesso che racconta, nelle differenti edizioni della sua autobiografia, che tra gli anni ’30 e ’60 del XVI secolo ebbe in progetto di scrivere un’opera aritmetica di carattere enciclopedico – l’Opus Arithmeticæ Perfectum – che però non verrà mai data alle stampe. Nell’autobiografia del 1544 troviamo scritto che il libro X dell’Opus Arithmeticæ Perfectum avrebbe dovuto essere una certa Ars Magna, composta da sessantasette capitoli (contro i quaranta dell’opera edita di cui disponiamo). I libri XIII e XIV dell’Opus Arithmeticæ Perfectum avrebbero dovuto invece essere dedicati a delle “questioni aritmetiche e geometriche” [nota 22]. Nell’Ars Magna poi, posteriore di un solo anno, viene specificato che la “questione aliza” fa parte delle “questioni geometriche”, con probabile riferimento proprio al libro XIV dell’Opus Arithmeticæ Perfectum [nota 23].

Secondo invece il manoscritto F.II.38.Nr.1, scoperto da Marialuisa Baldi e Guido Canziani nella Öffentliche Bibliotek Universität Basel e datato nei dintorni del 1550, il libro X dell’Opus Arithmeticæ Perfectum tratterebbe delle equazioni di secondo grado e della sola “regola aliza”. L’Ars Magna non è più nemmeno nominata [nota 24]. Infine, nelle ultime autobiografie del 1557 e 1562 si ritorna al quadro precedente in cui il libro X dell’Opus Arithmeticæ Perfectum è di nuovo l’Ars Magna e i libri XIII e XIV riguardano le questioni aritmetiche e geometriche [nota 25]. Nell’edizione del 1557 inoltre vengono trascritti gli incipit dei libri già composti e questo permette di identificare senza dubbi l’Ars Magna nominata con il testo edito a stampa nel 1545. Il rendiconto porta quindi a concludere che all’incirca dal 1550, forse addirittura dal 1545, fino al 1557 Cardano sperava di potere evitare il caso irriducibile e l’eventuale risultato sarebbe dovuto apparire sotto il nome di “aliza”. Inoltre, possiamo anche dedurre che degli scritti che vanno sotto il nome di “aliza” dovevano essere già stati composti prima del 1544. A partire dal 1557 sembra che Cardano perda questa speranza ed è molto probabile che, anche a causa delle sue vicissitudini personali, abbandoni del tutto la ricerca su questo tema.

Da quest’analisi emerge che Cardano si occupò a lungo, per circa una quarantina d’anni, delle questioni riguardanti le equazioni di terzo grado. Coniugando lo studio di equazioni particolari con l’indagine sulle possibili forme delle soluzioni e con le relazioni tra equazioni originate da sostituzioni, completa le soluzioni di Tartaglia costruendo un quadro teorico articolato per la risoluzione delle equazioni di terzo grado. Tuttavia, affinché il quadro sia completo, deve essere trovato un modo per venire a capo del problema posto dal caso irriducibile. I tentativi che Cardano mette in atto sono interessanti, indipendentemente dal risultato che non potrà raggiungere, perché mostrano che tipo di strumenti Cardano avesse a disposizione per maneggiare le equazioni.

BIBLIOGRAFIA

[1] Cajori F., Wantzel P.L., Bulletin of the American Mathematical Society, B24: 339-47, 1917-1918.

[2] Capelli A., Istituzioni di analisi algebrica, Pellerano, 1902.

[3] Cardano G., Libellus de Libris Propriis, 1544, 1663.

[4] Cardano G., Liber de Libris Propriis, 1557, 1663.

[5] Cardano G., De Libris Propriis, 1562, 1663.

[6] Cardano G., De Aliza regula Libellus, hoc est Operis Perfecti sui sive Algebraicæ Logisticæ, Numeros recondita numerandi subtilitate, secundum geometricas quantitates inquirenti, necesaria coronis, nunc demum in lucem editæ, 1570.

[7] Cardano G., Artis Magnae sive de regulis algebraicis, 1570, 1663.

[8] Cardano G., Ars Magna Arithmeticæ, seu Liber quadraginta Capitulorum & quadraginta Quæstionum, 1663.

[9] Cardano G., “Una quarta redazione del De Libris Propriis”, Rivista di storia della filosofia, 4: 767-98, 1998 (a cura di BaldiM. e Canziani G.).

[10] Cossali P., Origine, trasporto in Italia, primi progressi in essa dell’Algebra, Reale Tipografia Parmense, 1799.

[11] Cossali P., “Storia del caso irriducibile”, Istituto veneto di scienze, lettere ed arti, 1966 (a cura di Gatto R.).

[12] Ferrari L., Niccolò Tartaglia. Cartelli di sfida matematica, La Nuova cartografica, 1974 (riproduzione in facsimile delle edizioni originali del 1547-1548).

[13] Gavagna V., “L’Ars Magna Arithmeticæ nel corpus di Cardano”, in Massa-Esteve M. R., Rommevaux S., Spiesser M.: Pluralité ou unité de l’algèbre à la Renaissance, Champion, c.s.

[14] Gavagna V., “Medieval heritage and new perspectives in Cardano’s Practica arithmetice”, Bollettino di storia delle scienze matematiche, (1): 61-80, 2010.

[15] Hölder O., “Über den Casus Irreducibilis bei der Gleichung dritten Grades”, Matematische Annalen, 38: 307-12, 1891.

[16] Kneser A., “Bemerkungen über den Sogenannten casus irreducibilis bei cubischen -Gleichungen”, Mathematische Annalen, 41: 344-8, 1892.

[17] Loria G., Storia delle matematiche. Dall’alba della civiltà al secolo XIX, Hoepli, 1931, 1950.

[18] MacLean I., De Libris Propriis: The editions of 1544, 1550, 1557, 1562, with supplementary material, Franco Angeli, 2004.

[19] Maracchia S., Storia dell’algebra, Liguori, 2005.

[20] Mollame V., “Sul casus irreductibilis dell’equazione cubica”, Napoli Rend., 4: 167-71, 1890.

[21] Ruffini P., Teoria generale delle equazioni, in cui si dimostra impossibile la soluzione algebraica delle equazioni generali di grado superiore al quarto, Stamperia di S. Tommaso D’Aquino, 1799.

[22] Sansone G., Conti R., Lezioni di analisi matematica, CEDAM 1958.

[23] Tamborini M., “Per una storia dell’Opus Arithmeticae Perfectum”, in Baldi M., Canziani G.: “Cardano e la tradizione dei saperi”, Atti del Convegno internazionale di studi, Milano (23-25 maggio 2002), 157-190, Franco Angeli, 2003.

[24] Tartaglia N., Quesiti e inventioni diverse, Ateneo di Brescia, 1959 (riproduzione in facsimile a cura di A. Masotti della seconda edizione del 1554).

[25] Toscano F., La formula segreta. Tartaglia, Cardano e il duello matematico che infiammò il Rinascimento, Sironi, 2009.

NOTE

[1] “Scipione del Ferro di Bologna già quasi trent'anni fa scoprì la soluzione di questa equazione. In verità la trasmise ad Antonio Maria Fior di Venezia, che, scontratosi una volta in una disputa con Niccolò Tartaglia di Brescia, fornì l'occasione a Niccolò di trovarla. Niccolò, tacendo la dimostrazione, la trasmise a noi dietro nostra richiesta. Noi, contando su questo aiuto, cercammo la dimostrazione e, ottenuta in un modo che fu difficilissimo, laesponiamo come segue” [7, cap. XI].

[2] Per una cronologia dettagliata, cfr. [19, p. 248]. La ricostruzione storica si basa su [7, capitoli I e XI], [12] e [24].

[3] Come conseguenza di una scelta stilistica e concettuale, tradurremo il linguaggio matematico dell’epoca nel nostro ogni volta che il vantaggio in termini di facilità di comprensione per il lettore non invalidi il rigore dell’attinenza al testo.

[4] Nell’ordine, si tratta di [7, capp. XI-XXIII].

[5] Limitiamo la discussione alle equazioni che sono effettivamente di terzo grado, tralasciando le spurie e le trinomie riducibili della forma a2nx²ⁿ + anxⁿ + a0 = 0.

[6] Tra gli altri, cfr. [2, pp. 600-604] oppure [22, pp. 507-12] oppure [19, pp. 569-81].

[7] Più precisamente,

[8] Infatti, il sistema dato da:

è sempre risolubile in C.

[9] Vale a dire ω³ = 1 e ω^k ≠ 1 per k = 1, 2. In particolare, se ω è una radice cubica primitiva dell’unità, allora ω = – 1/2 + i √3/2 e ω² = – 1/2 – i 3/2.

[10] Per comodità, discutiamo la natura delle soluzioni di (2), poiché a2/3a3 appartiene a R è ininfluente. Se Δ3 > 0, allora ³√t1, ³√t2 appartengono a R. Quindi:

e y2 è il coniugato di y3 .

[11] Infatti, se Δ3 = 0, allora

Quindi:

[12] Per ulteriori dettagli si veda ad esempio [10, cap. V.4, p. 291].

[13] Tuttavia queste ragioni, soprattutto la prima, valgono anche per l’Ars Magna e non giustificano la pubblicazione qualche anno più tardi. Se è vero infatti che quest’ultima si inserisce nel progetto editoriale dell’Opus Arithmeticæ Perfectumcome libro X, il caso irriducibile rimane ancora un problema aperto. È probabile quindi che Cardano abbia deciso in breve tempo di pubblicare l’Ars Magnaper assicurarsi la paternità delle formule risolutive per le equazioni di terzo grado, dopo aver avuto notizia che Tartaglia aveva completato la traduzione con commento degli Elementi di Euclide e l’edizione latina di parte del corpus archimedeo e che era quindi libero di dedicarsi a un proprio libro sulle equazioni. Cfr. [13].

[14] E che di fatto usa per 16x = x³ + 21 e x³ = 16x + 21, cfr. [7, cap. XXV.10]. Per un commento, cfr. [10, vol. II, cap. VII, articolo I, pp. 325-7] e [19, pp. 278-9]

[15] Cfr. [8, cap. XXXI.1] ma anche il già citato [7, cap. XXV.10] e [6, cap. V e XIV].

[16] Cfr. [10, vol. II, p. 442] e [11, p. 27].

[17] Ringraziamo Paolo D’Alessandro per aver confermato con un’etimologia precisa l’ipotesi di Cossali secondo cui “aliza” significa “irresolubile”, contro l’ipotesi di Gino Loria secondo cui “aliza” deriverebbe piuttosto dall’arabo e significherebbe difficile. Cfr. [10, vol. II, p. 441], [11, cap. I, par. 2, p. 26] e [17, p. 298].

[18] “Daccapo, ripetendo cose già dette, sia il cubo a d dalla linea a c divisa in tre parti. È chiaro che ci saranno quattro parti principali diverse, il cubo a b, il cubo b c, tre volte a b per il quadrato b c e tre volte b c per il quadrato a b. Bisogna quindi adattare il numero e questo può essere fatto in sette modi più facili, come abbiamo detto. Se non possiamo trovare la soluzione nel modo più facile, come potremmo trovarla in un modo più difficile?” [6, cap. I].

[19] Secondo la terminologia di Cossali.

[20] Per y = AB e z = BC: “Ma siccome i cubi a b e b c non possono mai essere minori della quarta parte di tutto il cubo a d, e ciò non succede se non quando a c è divisa in parti uguali in b. Perciò quando il numero è minore di un quarto di tutto il cubo a d non può essere uguagliato ai cubi a, b, b c. E perciò questa soluzione è in parte non generale”, [6, cap. I].

[21] Infatti: Verificando la condizione di normalità, abbiamo che:

Verificando la condizione di normalità, abbiamo che:

[22] “(...) il decimo è intitolato Ars magna, contiene sessantasette capitoli, (...) il tredicesimo e il quattordicesimo sono destinati a questioni aritmetiche e geometriche” [3, paragrafo 33]. Nasce qui il problema di capire a cosa esattamente si riferisse questa Ars Magna di sessantasette capitoli. È molto probabile che ci fosse un legame con parte dell’Ars Magna Arithmeticæ quale la conosciamo oggi. Per alcune ipotesi al riguardo, cfr. [23], [18] e [13].

[23] “(…) allora questo è risolto tramite la questione Aliza, della quale si tratta nel libro delle questioni geometriche” [7, cap. XII].

[24] “In tutti i dieci capitoli sul quadrato insieme con la regola Aliza [9, p. 793].

[25] “Il decimo, il cui inizio è “Questa arte un tempo da Maometto, 83 folii (...)”. Il quattordicesimo [sulle cose] geometriche” [4, paragrafo 26] e “Il decimo sulla regola magna, e perciò chiamato ars magna, ed è il solo edito tra tutti (...). Il quattordicesimo [sulle cose] geometriche” [5, paragrafo 11.8].