Con la calcolatrice, senza libro di testo

1. L’ipotesi NT

Ho la fortuna di insegnare matematica al tempo stesso in un triennio di liceo scientifico e al primo anno di una Università di Economia. Godo quindi di una posizione di privilegio da cui osservare i mutamenti degli ultimi anni.

La riforma universitaria, attuata in un periodo storico che vede esplodere i problemi didattici e logistici legati alla scolarità di massa, ha mutato, in qualche caso radicalmente, lo scenario dell’insegnamento della matematica. La laurea triennale ha imposto in alcuni casi riduzioni al numero di crediti dei corsi di matematica, anche se non sempre questi tagli si sono tradotti in proporzionali riduzioni quantitative dei contenuti trasmessi. Si è reso necessario non solo un ripensamento di modi e tempi di trasmissione del sapere ma anche una riorganizzazione di programmi, contenuti e strumenti di valutazione; anche in Università si è cominciato a parlare di "nuclei fondanti" dei vari insegnamenti, espressione centrale nel glossario della "riforma dei cicli".

È evidente quali siano sempre state le contraddizioni e le difficoltà dell’insegnare matematica in un corso di laurea in Economia: si ha un bel dire che la matematica è utile e pervasiva, che qualunque strumento di indagine razionale sui mercati economici e finanziari esige una buona conoscenza della matematica e dei suoi strumenti, che la matematica è comunque formativa e "insegna a ragionare". È inutile nasconderci il fatto che la matematica non è la materia più amata dagli italiani, che da sempre ha svolto un ruolo di disciplina selettiva, che il corso di Matematica Generale per molti anni ha ottenuto la palma di corso meno efficiente di tutta l’università per quanto riguarda il rapporto tra numero di promossi e numero di studenti esaminati.

E non è davvero facile convincere gli studenti della pretesa utilità della matematica quando il calcolo differenziale viene preceduto dalla teoria e -d dei limiti di funzioni, quando vengono richieste dimostrazioni di teoremi di cui molti studenti non hanno compreso l’enunciato (valga per tutti il teorema di Lagrange), quando si fa ricorso a metafisici oggetti come gli "o piccolo" e a simboli dalla scarsa efficacia didattica come dy/dx, oppure 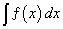, oppure a vetusti armamentari algoritmici come il teorema di Kronecker per il rango di una matrice.

Spesso lo studente ha l’impressione che il corso di matematica sia una cerimonia interna alla comunità dei matematici, senza riflessi sulla reale preparazione curricolare, una dolorosa necessità nel proprio cammino scolastico. Vorrei dire che agli occhi dello studente questa cerimonia ha il sapore di una meta-matematica fatta di pignolerie, cavilli formali e di facciata che nascondono un certo vuoto semantico, di estenuanti impalcature preliminari alla fine delle quali non c’è nulla. Ma siccome la matematica continua a detenere indiscusso prestigio intellettuale e accademico (e questo è davvero un gran bel mistero) nessuno ha il coraggio di dire o di pensare che il Re è nudo, che per decenni l’insegnamento della matematica non ha lasciato dietro di sé, in buona parte degli alunni, alcuna conoscenza culturalmente spendibile.

Bene, partiamo da qui: è necessario cambiare, è in gioco la credibilità del sistema scolastico e universitario e più in particolare dell’insegnamento della matematica.

La tesi di questa comunicazione non è soltanto un generico appello al fatto che le nuove tecnologie aprono orizzonti nuovi e positivi sia al miglioramento del rapporto studenti-matematica, sia all’efficacia dei meccanismi di insegnamento-apprendimento.

Il problema che vorrei sollevare è il seguente: ipotizziamo che lo studente abbia a disposizione, in tutte le fasi del processo di apprendimento (durante la lezione, nella preparazione individuale, all’esame) uno strumento in grado di:

• effettuare calcolo numerico
• svolgere calcolo simbolico
• tracciare ed esplorare grafici
• accettare funzioni definite dall’utente
• eseguire semplici programmi

Sotto questa ipotesi, che chiamerò ipotesi NT (nuove tecnologie), come cambia un corso di matematica? Come cambiano i contenuti, la presentazione dei concetti fondamentali, gli esercizi e problemi da proporre, gli strumenti di valutazione?

2. L’esperienza al Liceo Scientifico

Da tre anni adotto, a partire dalla terza (si tratta di un corso tradizionale, tre ore alla settimana), la TI-89, una calcolatrice grafico-simbolica che ha tutte le potenzialità sopra elencate (e molte altre). Mi trovo quindi esattamente nell’ipotesi NT: ogni studente ha il proprio strumento a scuola, a casa, durante la prova scritta.

Che cosa è cambiato? Molto.

1) È migliorato l’interesse per la matematica da parte degli studenti, e quindi il profitto. Questi ragazzi, cresciuti tra telecomandi e tastiere di telefonini rivelano un’abilità sorprendente (inimmaginabile in un adulto) nell’imparare rapidamente la sintassi dello strumento. Non ci sono più, quindi, fasi preliminari (come accadeva con il Pascal) in cui si attua l’approccio sintattico allo strumento: si fa matematica dal primo giorno, con una certa curiosità che permane nel tempo, a mano a mano che si scoprono nuovi ambienti e nuove funzionalità.

2) Le approssimazioni sono diventate essenziali. Il percorso didattico invita in modo naturale a trattare numeri decimali e approssimazioni.

Per esempio lo studente scopre subito che, se la calcolatrice è impostata in "AUTO" (cioè se restituisce output simbolici a input simbolici e output numerici a input numerici) le funzioni "seno" e "coseno" agiscono in modo differente al variare dell’angolo: a volte non semplificano e restituiscono lo stesso input.

Succede allora che ci si abitua a forzare in ogni caso il risultato numerico (c’è un apposito tasto), e si perde così la nozione di "angoli notevoli".

La velocità istantanea di un moto in un certo istante viene innanzitutto approssimata mediante la velocità media in un intervallo simmetrico via via più piccolo. Per esempio, per il moto armonico

s(t) := 5 cos(p /2 t)

nell’istante 0.5 s

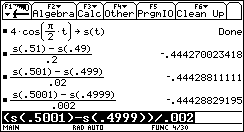
Ugualmente la pendenza di una funzione in un punto si approssima mediante il rapporto incrementale simmetrico. Ecco l’approssimazione della pendenza di f(x):=x^3- 2x+1 nel punto di ascissa x0:=2.

3) Cambia radicalmente (si rafforza) l’attenzione all’aspetto algoritmico degli oggetti matematici. Lo studente è cronicamente pigro: se un certo risultato si può ottenere in modo meccanico state pur certi che ogni studente si sforzerà di implementare la relativa funzione o il relativo programma. Ci sono in questo aspetti positivi e negativi.

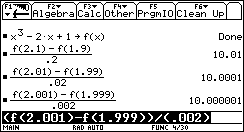
• Alcuni studenti iniziano un percorso di sfida con la calcolatrice, imparano per proprio conto a programmare e acquisiscono in breve tempo competenze e abilità che sono inevitabilmente anche di carattere matematico (ad esempio la capacità di individuare e di scegliere gli argomenti di una funzione, la capacità di scegliere la miglior struttura dati). Cito un esempio: uno studente automatizza il processo di approssimazione della pendenza di una funzione in un punto definendo una propria funzione che chiama KURT (non chiedetemi perché):

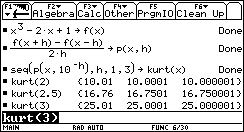
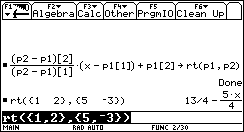
Si capisce che occorre esprimere i coefficienti dell’equazione in funzione delle coordinate dei punti. Che cosa succede se si passa alla funzione quadratica per tre punti? Ci si può accorgere per esempio che è meglio fornire in ingresso due dati: la lista delle ascisse e la lista delle ordinate anziché una lista per ciascun punto.

Insomma, gli aspetti algoritmici finiscono per diventare importanti, spesso più importanti degli aspetti di semplificazione algebrica delle espressioni che si calcolano. Un nuovo "lessico familiare" si impone in classe: è quello degli strampalati nomi che gli studenti danno alle loro procedure, e che scrivono nei compiti in classe.

• Ma ci sono anche aspetti negativi: alcuni studenti finiscono per affidare alle funzioni della calcolatrice (che tra studenti diventano merce di scambio, come gli appunti) porzioni eccessive di conoscenze. Un esempio riguarda l’equazione della retta tangente ad una curva: la calcolatrice è in grado, in ambiente grafico, di determinare (in forma numerica) l’equazione della retta tangente ad una curva in un punto. Per esempio la retta tangente a f(x)=2^x in x0=1.

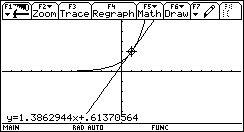
Ecco un problema didattico interessante: come cambia l’intero percorso del tema calcolo differenziale se lo studente può accedere senza conoscenze particolari all’equazione della retta tangente ad una curva, oppure, in modo ugualmente semplice, alla derivata di una funzione, al polinomio di Taylor, all’integrale definito e indefinito?

Una risposta potrebbe essere: finalmente liberati dalle necessità di calcolo bruto, possiamo puntare maggiormente all’aspetto semantico degli oggetti matematici.

Un'altra risposta: possiamo fare più matematica di prima; ad esempio, possiamo utilizzare lo strumento derivata per mostrare l’algoritmo di Newton nell’approssimazione dello zero di una funzione, possiamo affrontare per esempio l’affascinante problema dell’approssimazione polinomiale di una funzione trascendente.

Ancora: possiamo chiederci (domanda fatidica, problema centrale) che cosa fa la calcolatrice quando ci fornisce l’approssimazione alla 13ª cifra decimale di ?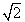

Si affaccia timidamente anche un’ipotesi più radicale: ridimensionare il peso quantitativo del calcolo infinitesimale nei curriculum (segretamente lo studente pensa: "Quante storie per trovare un massimo, il grafico sulla calcolatrice mi fa vedere con la precisione che voglio dove sta il massimo ..."). Non sentiamoci inorriditi da questa ipotesi: non dobbiamo temere, anzi dobbiamo scontrarci con questi nodi. Il calcolo infinitesimale è una delle conquiste più straordinarie del pensiero scientifico occidentale, dobbiamo chiederci in che modo tale conquista sopravvive nell’era dei computer: è tempo di ripensarne sia la struttura didattica sia i metodi di approccio.

Una cosa è comunque certa: le forme di valutazione devono cambiare. Nell’ipotesi NT gli attuali temi alla prova scritta di matematica dell’Esame di Stato appaiono incongrui (ricordo che a tutt’oggi sono vietate all’Esame di Stato persino le calcolatrici grafiche). Per esempio: quasi ogni problema d’esame che riguardi le funzioni si conclude con la fatidica domanda "Si calcoli la regione finita di piano delimitata da ... ". È ovvio che sono in gioco due competenze distinte:

a) tradurre l’area richiesta con un integrale definito (sono in gioco forti competenze di carattere semantico);

b) "calcolare" tale integrale, il che non significa affatto "misurare", "valutare", "stimare"; nelle tacite convenzioni ministeriali significa esprimere tale numero in forma simbolica mediante le funzione elementari.

Continuo a dire ai miei studenti di quinta che devono tenere ben distinte le due richieste: scrivere l’integrale definito che traduce un’area è una forte competenza matematica ed è il cuore della risposta; ad essa assegno un peso valutativo considerevole. Calcolare tale integrale, cioè determinare una primitiva è competenza diversa, e in definitiva trascurabile rispetto alla prima.

Nell’ipotesi NT non posso limitarmi a chiedere di studiare una funzione, di determinare l’equazione della retta tangente ad una curva in un suo punto, lo studente può rispondere senza particolari conoscenze. Posso allora (per esempio) chiedere di utilizzare la retta tangente come strumento di approssimazione:

Sia data la funzione f(x):=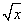. Approssimare il numero 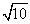utilizzando la retta tangente a f(x) nel punto di ascissa x0=9 e calcolare l’errore relativo. Stabilire per quali valori x compresi nell’intervallo [9, 16] l’approssimazione di 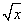è migliore sulla retta tangente in 9 anziché sulla retta tangente in 16.

4) Cambia anche l’approccio didattico quotidiano alla matematica, che diventa inevitabilmente meno deduttivo e sempre più fondato su "esperimenti". Ecco, c’è una novità dirompente: si possono fare subito esperimenti, tentativi e anche errori senza danni. Osservo che molto spesso lo studente vuole controllare subito sulla calcolatrice quanto l’insegnante va dicendo, mosso un po’ dal desiderio di coglierlo in errore, un po’ dalla curiosità di arrivare prima dell’insegnante al risultato. Si osservi che in questa situazione la calcolatrice gioca il ruolo di "terzo polo" nella dinamica studente-insegnante: è un fatto completamente nuovo e positivo, che rafforza l’autonomia e in certa misura la sicurezza dello studente. Certo la concentrazione collettiva della classe si disperde, ma questo forse non è un male.

Si è detto da più parti che occorre predisporre ambienti di apprendimento nei quali sia favorita la formulazione di congetture: sono del tutto d’accordo. Poche attività come quella di formulare congetture rafforzano una preparazione scientifica. Per formulare congetture occorre aver capito il problema, averlo rappresentato mentalmente, aver escogitato una strategia. Dopo aver formulato una congettura occorre validarla oppure falsificarla, scegliendo prove significative. Se la congettura regge ci si chiede perché funziona? Funziona sempre? Ci si avvicina all’esigenza di una dimostrazione. Una congettura sbagliata ma sensata è molto più importante per valutare il processo di apprendimento di mille esercizi "giusti".

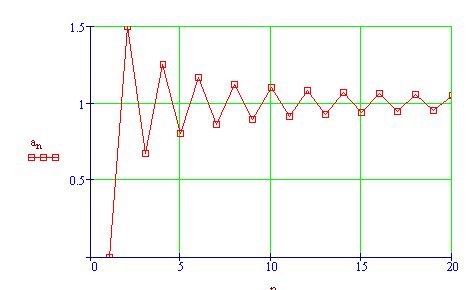
5) Un altro cambiamento significativo riguarda l’attività di rappresentazione e interpretazione dei dati. Abbiamo la possibilità di passare quasi immediatamente dalla tabella al grafico, favorendo così un’attività che è nuova nel panorama didattico: stabilire una funzione che si adatti al meglio ai dati. I dati possono essere recuperati ovunque: in un esperimento fisico, in una descrizione statistica, anche all’interno della stessa matematica.

Lasciatemi svolgere un esempio: se approssimo la pendenza di f(x):= 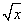in x0=1 mediante il rapporto incrementale simmetrico

p(h) :=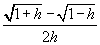

come varia l’errore al variare di h?

Ipotizziamo che la pendenza valga esattamente 0.5, come si può ricavare da qualche esperimento.

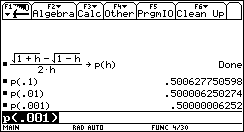
Valutiamo l’errore:

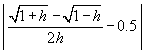
con h=0.2, 0.15, 0.1, 0.05, 0.01.

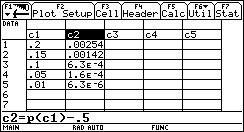
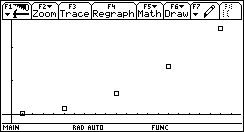
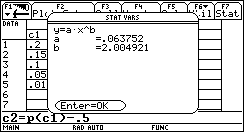
I punti, disposti in modo regolare, ci suggeriscono l’idea che sia possibile dare un modello ai dati: quale curva meglio si adatta ad essi? Che tipo di crescita osserviamo al crescere di h? Potrebbe essere una crescita esponenziale? È importante osservare il comportamento in h=0: al tendere di h a 0 l’errore tende a 0, possiamo pensare allora ad una funzione potenza

h -> ah^b,

con a e b da determinare. La "miglior" funzione potenza (secondo il metodo dei minimi quadrati) che approssima i dati è una funzione quadratica: 0.06h².

In definitiva: nell’ipotesi NT vi sono cambiamenti radicali nell’organizzazione di un corso di matematica. Tali cambiamenti non riguardano solo i contenuti, i metodi, la valutazione. Riguardano anche gli stessi oggetti matematici, l’immagine che di essi gli studenti rappresentano mentalmente, la rete concettuale che li collega, la sintassi che li governa. Insomma, cambia la matematica stessa, proprio nel solco della tradizione: dai tempi della riga e del compasso, su cui Euclide ha costruito la sua geometria, l’esperienza e gli strumenti che la matematica produce hanno guidato la ricerca e indicato nuovi oggetti.

3. L’esperienza in Bocconi

La Bocconi ha scelto (per vari motivi che qui non ci interessano) il software MATHCAD, della MathSoft Inc., come testa d’ariete per far sì che i docenti (prima) e gli studenti (poi) iniziassero a sfruttare le possibilità e i vantaggi offerti dal calcolo automatico (più in generale dall’Informatica), nell’insegnamento e nell’apprendimento della matematica.

Mathcad è un potente software di calcolo numerico e (solo parzialmente) di calcolo simbolico (il calcolo simbolico di Mathcad sfrutta il kernel di Maple V, della Waterloo Maple Inc.). Il foglio di lavoro simula il foglio bianco con il quale il matematico si accinge a risolvere un problema con carta e penna. Si può scrivere in un punto qualsiasi del foglio: i calcoli svolti, le assegnazioni effettuate, i grafici tracciati sono memorizzati e influenzano tutto ciò che si trova a destra e sotto il punto in cui le formule sono state immesse.

Ho avuto la ventura di guidare la prima fase, quella di guida alla preparazione dei docenti (circa 12) del corso di Matematica Generale (primo anno, 8 crediti, solito programma che comprende successioni, serie, calcolo differenziale e integrale, algebra lineare).

In sostanza: dopo alcune lezioni di introduzione alla sintassi di Mathcad (invero molto semplice ad un primo approccio) sono stati preparati e distribuiti ai docenti su CD un certo numero di fogli di lavoro, divisi per argomenti secondo l’indice del manuale in uso. Ogni docente, ovviamente in piena libertà e autonomia, sceglieva quanti e quali file utilizzare in aula (ogni aula è dotata di PC e di proiettore). Siamo quindi ancora ben lontani dall’ipotesi NT, ma soltanto questo primo approccio ha avuto una immediata ricaduta sul programma del corso, che ha subìto una significativa ristrutturazione. L’esperienza è stata positiva: nonostante qualche docente recalcitrante, nel complesso tutti hanno apprezzato le possibilità offerte da questo software che consente di mostrare agevolmente calcoli, grafici e animazioni, dando così al docente la possibilità di essere più convincente (e anche più avvincente) e di poter trattare senza difficoltà esempi e problemi anche complessi dal punto di vista numerico, come spesso accade per gli esempi finanziari.

Questo è il primo passo: il docente si impadronisce della sintassi del nuovo strumento e crea messaggi semantici a sostegno della propria lezione. Le nuove tecnologie svolgono qui il ruolo di "superlavagna", uno strumento volto a migliorare l’insegnamento-apprendimento.

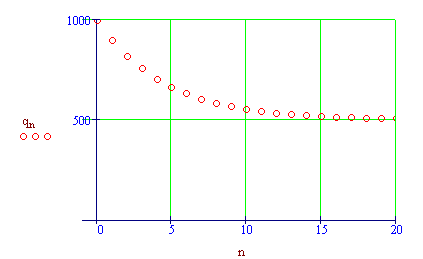
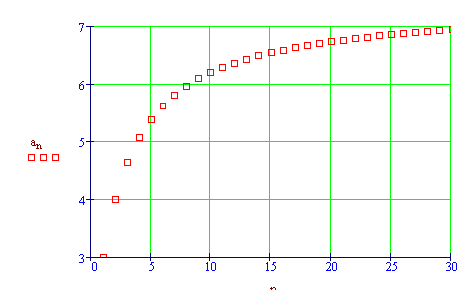
Alcuni docenti hanno sottolineato, per esempio, come la rappresentazione grafica delle successioni sia stata efficace per mostrare rapidamente concetti come "convergere per eccesso, per difetto", "né per eccesso né per difetto ".

Ora si sta discutendo di come consolidare e soprattutto allargare agli studenti questa esperienza.

Per rispondere alla domanda del convegno: è questa "nuova didattica"?

No, non c’è nulla di sostanzialmente nuovo rispetto a quanto ogni buon docente ha sempre fatto: dotarsi di qualunque strumento (reale o mentale, dadi, ruote, chitarre o pianeti) per fare esperimenti durante la lezione, per arricchire negli studenti la rappresentazione mentale degli oggetti matematici.

4. Nuove tecnologie = Nuova didattica?

Che cosa allora è "nuova didattica"?

La novità didattica presente nell’ipotesi NT, lo ricordo, è quella di presupporre che lo studente possa servirsi dello strumento di calcolo automatico durante tutte le fasi del processo di apprendimento, e in particolar modo durante l’esame.

Questa ipotesi ci costringe alla seguente domanda: quali competenze e soprattutto quali abilità di calcolo possiamo trasferire allo strumento automatico? Non è davvero facile rispondere (anche perché sto pensando ad un corso di laurea, quello in Economia, in cui la matematica è disciplina di servizio); dovremo operare scelte precise e assumercene la responsabilità, perché una immediata conseguenza di quelle scelte dovrà tradursi in prove di valutazione in cui saggeremo sia la capacità dello studente di sfruttare gli strumenti di calcolo per risolvere un problema, sia le conoscenze matematiche acquisite. In definitiva: lo strumento di calcolo non è soltanto uno strumento in più, non è solo consigliato, ma è prescritto. Ecco, forse questo è il nodo da sciogliere: vogliamo prescrivere anche l’utilizzo di uno strumento di calcolo.

Mi spiego con un esempio: lo studente deve saper calcolare con carta e penna il rango o il determinante di matrici molto semplici. Deve conoscerne la definizione e deve avere l’esperienza di ambienti significativi in cui utilizzarle quegli strumenti. Al tempo stesso deve dimostrare di saper calcolare ranghi e determinanti di matrici comunque complesse utilizzando uno strumento di calcolo, così come deve saper risolvere qualunque sistema lineare. Ecco che il cosiddetto "teorema di Kronecker" può andare in soffitta senza rimpianti.

Capite bene che la definizione di un oggetto matematico (croce e non delizia di tutti gli esami orali: "Che cosa significa che una successione converge a 5?", "Che si avvicina a 5!") assume, se è possibile, un valore ancora più rilevante; se non sono più richiesti calcoli complessi o difficili con carta e penna è ancor di più tassativo sapere che cos’è quell’oggetto.

Non dobbiamo più insegnare pesanti algoritmi con carta e penna: sono i leggerissimi bit a svolgere questa funzione; dobbiamo (e abbiamo maggior tempo per farlo) occuparci finalmente a tempo (quasi) pieno della semantica dei concetti che vogliamo comunicare.

Utilizzando questa chiave di lettura possiamo rileggere i nostri programmi, i nostri percorsi didattici e ad ogni passo chiederci: che cosa è bene che lo studente sappia calcolare con uno strumento elettronico? È un’avventura perigliosa e affascinante ¼

Solo per fare qualche esempio, mi piacerebbe che uno studente sapesse calcolare o approssimare, con la TI-89 o con Mathcad:

• il ventesimo elemento della successione ricorsiva a0:= 0.8, an+1:=4an(1- an);
• la derivata n-esima di ¦ (x):= ;
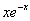• l’integrale di 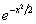da 1 a 3;
• il polinomio di Taylor di una funzione in un punto;
• il polinomio di grado n che passa per n+1 punti;
• la somma dei cubi dei primi n numeri naturali;
• la soluzione dell’equazione 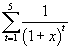= 0;
• la potenza A¹⁰ di una matrice quadrata A;
• la somma di ;
• ...

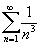Per oltre un secolo siamo stati prigionieri degli epigoni di Hilbert. Abbiamo trasformato una materia che è l’emblema della curiosità intellettuale, della ricerca e della scoperta in un insegnamento fatto di aride impalcature sintattiche. Abbiamo trasformato la matematica in logica, abbiamo trasformato la matematica in una meta-matematica, a guardar bene, molto poco "rigorosa".

Oggi, a differenza di quanto accadeva quando eravamo noi studenti (allora la "cultura" si auto-giustificava), gli studenti chiedono in continuazione "a che cosa serve?". Possiamo far valere il principio di autorità e zittire l’interlocutore sostenendo che "ciò che si impara non deve servire a qualcosa", oppure possiamo porci davvero questa domanda cercando di estraniarci e di osservare tutta l’istituzione scolastica e accademica dall’esterno. Se non riusciamo a rispondere a questa semplice domanda, che vuol dire molto di più di quanto appaia, non saremo in grado di superare positivamente la riforma che coinvolge in questi anni scuola e università. Un modo di rispondere, come sempre, è quello di partire dal fondo, chiederci perché insegnare matematica oggi, con quali scopi e lungo quali percorsi educativi.

Può darsi che sia giunto il momento rompere questo sciagurato patto che ci ha costretto a considerare la logica preliminare e presupposto per la matematica: vogliamo fare matematica, non sopportare noiosissime cerimonie in cui si insegna il bon-ton del buon matematico.

Le nuove tecnologie potrebbero costituire, in questa delicata fase di rinnovamento, il paradigma del "fare matematica". Se so che cosa voglio, se rispetto una sintassi, posso ottenere rapidamente un risultato: questo arricchisce la mia esperienza, mi avvicina a problemi più complessi, mi rende più autonomo.