Costanti matematiche e aree delimitate da un'iperbole equilatera

Nel 1949 Giovanni Vacca, mio padre, dedusse che dalla equazione dell’iperbole equilatera  xy = 1  si possono determinare tre costanti matematiche. La prima è pi greco. La seconda è il logaritmo naturale di 2. La terza è la costante di Eulero (γ = 0,57721…. )  definita come

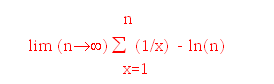
utile a chi usa le funzioni di Bessel (che servono fra l’altro a calcolare la densità di corrente elettrica ad alte frequenze nella sezione di un conduttore). Menzionò questo risultato nel suo articolo “La costante di Eulero e l’aritmetica analitica” negli  Atti della XLII riunione della SIPS tenutasi a Roma nel 1951. Io lo lessi solo nel 2006.

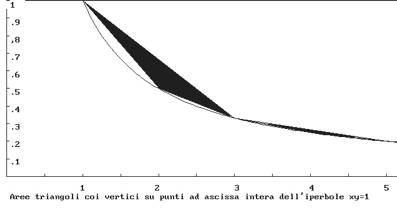
Nella figura qui sopra è disegnata la curva che rappresenta l’iperbole:

xy = 1

Passa per i punti definiti dalle coppie di valori di   x  e   y: (1,1), (2, ½). (3, 1/3), (4, ¼), (5, 1/5) ecc. Prendiamo ora  i punti della curva che hanno ascissa intera:  1, 2, 3, 4, 5, 6, 7, ecc. e uniamoli con segmenti (che sono corde dell’iperbole). Se calcoliamo la somma delle aree comprese fra tutte queste corde e la curva stessa (fino all’infinito; le prime 2 aree sono bianche in figura) otteniamo:

γ – ½       =  0,07721566490153286 ……

dove γ è la costante di Eulero. Lo conferma il programma seguente in Qbasic che dopo 2 milioni di iterazioni dà 12 cifre decimali esatte.

S = 0:  a = 1 : b = 2: m = LOG(a): n = LOG(b)

11 Lb = LOG(b): La = LOG(a)

w = (a/(2 * b)) - (b/(2 * a)) + ((a+b) / a) - ((a + b) / b) - Lb + La

S = S + w: PRINT S

a = a + 1: b = b + 1 : GOTO 11

Se si sommano le aree dei triangoli che hanno i vertici su tre punti consecutivi ad ascissa intera, (123, 345, 567, ecc.; i primi due sono anneriti nella figura precedente), si ottiene:

log2 – ½  =  0,193147180559945309 ……..

Il programma per controllarlo (dopo 2 milioni di iterazioni, dà 11 cifre esatte) è:

S = 0 : a = 1

11 w = (2 / a) - (4 / (a + 4)) + (2 / (a + 8))

S = S + w: PRINT S: a = a + 2

GOTO 11

Se si sommano le aree dei triangoli che hanno i vertici su tre punti ad ascissa intera presi saltandone uno a ogni passo (135, 579, 9 11 13, ecc.) si ottiene

p/2 – 1     = 0,570796326794897 …….

Nel diagramma seguente è evidenziato in nero il primo triangolo della sequenza citata con vertici nei punti dell’iperbole che hanno ascissa 1, 3  e 5.

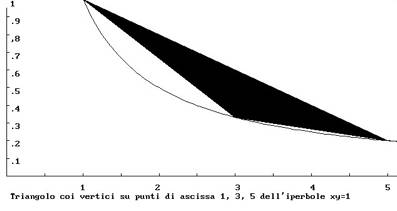
Il programma per controllarlo è:

S = 0: a = 1

11 w = (1 / a) - (2 / (a + 2)) + (1 / (a + 4))

S = S + w: PRINT a: PRINT w : PRINT S: a = a + 4

GOTO 11

Ho scritto un altro programma per calcolare la somma delle aree dei triangoli i cui vertici sono sempre sull’iperbole  xy = 1, partendo da 1 e saltandone due (cioè usando i triangoli 1 4 7, 7 10 13, 13 16 19, ecc). Il risultato è:

1,0069465447….

La somma delle aree dei triangoli i cui vertici sono sempre sull’iperbole  xy = 1, partendo da 1 e saltandone tre (cioè usando i triangoli 159, 9 13 17, 17 21 25, ecc), ha il valore:

1,4678919493…

La somma delle aree comprese fra le corde che congiungono i punti ad ascissa intera sempre sull’iperbole  xy = 1, partendo da 1 e saltandone due e la curva stessa, ha il valore:

0,533421491349…

La somma delle aree comprese fra le corde che congiungono i punti ad ascissa intera sempre sull’iperbole  xy = 1, partendo da 1 e saltandone tre e la curva stessa, ha il valore:

0,8411591722531 …

Non mi sembra che questi quattro valori siano in alcuna relazione semplice con alcuna costante matematica. Se qualcuno ha la pazienza di ragionarci sopra, è probabile che trovi altre relazioni di un certo interesse.