Dalla rappresentazione binaria a quella frattale

Con il termine frattale vengono indicati quegli oggetti geometrici dotati di alcune caratteristiche peculiari come l'autosimilarità e una dimensione frazionaria (da cui deriva il termine frattale). Ingrandendo quindi una qualsiasi sua parte, si ottiene una figura simile a quella originale. Per questo motivo la sua forma non dipende dalla scala di grandezza utilizzata.

Frattale di Mandelbrot

Vediamo ora di definire la dimensione di autosimiliarità: se consideriamo un segmento nella la dimensione euclidea D=1 di lunghezza 1 e riduciamo la sua lunghezza di 1/2, occorreranno 2 segmenti per ottenere il segmento originale, entrambi della lunghezza 1/2. Riducendo la dimensione di 1/4, occorreranno 4 segmenti e così via fino al caso generale che prevede N=R segmenti di dimensione di 1/R. In modo analogo prendiamo un oggetto nella dimensione euclidea D=2: il quadrato. Se riduciamo la dimensione di 1/2, occorreranno 4 quadrati con lato 1/2. Se riduciamo la dimensione di 1/4, occorreranno 16 quadrati con lato 1/4. In fine se riduciamo la dimensione di 1/R, occorreranno N=R² quadrati con lato 1/R. Il discorso vale anche se consideriamo un cubo nella dimensione euclidea D=3. Infatti si ottiene che da una riduzione della dimensione di 1/R, bisognerà utilizzare N=R³ cubi di spigolo 1/R. In generale, se prendiamo un oggetto unitario con dimensione euclidea D, e riduciamo la sua dimensione lineare di un fattore 1/R in ogni direzione spaziale, occorreranno N=R^D oggetti simili all'oggetto originale per ricomporre quest'ultimo. Da questa uguaglianza scaturisce la dimensione frattale¹: D=log⁡(N)/log⁡(R).

Il frattale di Sierpinski

Un matematico polacco, Wacław Franciszek Sierpiński, nei primi anni del 1900, si interesso ad un particolare frattale ottenuto per via geometrica elementare suddividendo un triangolo equilatero in 3 triangoli simili di dimensioni dimezzate rispetto al triangolo da cui essi sono stati generati. Ripetendo tale procedimento per passi successivi si ottiene una struttura frattale.

Considerato che in ogni passaggio il triangolo generato ha dimensioni dimezzate rispetto a quello precedente si avrà un rapporto di omotetia R=1/2. Poiché in ogni passaggio vengono generati da ogni triangolo altri 3 triangoli simili ma di dimensioni ridotte, si avrà N=3. Da ciò scaturisce che la dimensione frattale vale D=log⁡(3)/log⁡(2) che è un numero irrazionale.

Vediamo ora come poter costruire un frattale di Sierpinski con un procedimento algebrico che prevede l'utilizzo di numeri binari. Ricordiamo che il sistema numerico che normalmente utilizziamo a scuola e nella quotidianità, è quello decimale, che prevede l'utilizzo di 10 simboli (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Un sistema numerico binario invece utilizza solo 0 e 1. Tale sistema è famosissimo perché è alla base del funzionamento degli attuali calcolatori.

Ricordiamo che per rappresentare in binario un numero decimale, bisogna dividerlo ripetutamente per 2 e memorizzare i resti delle divisioni ottenendo una successione di simboli 0 e 1. Ad esempio il numero decimale 13 sarà rappresentato in binario con [1,1,0,1] (n-pla di lunghezza 4).

Date due n-ple della stessa lunghezza (u, v), possiamo considerare la funzione:

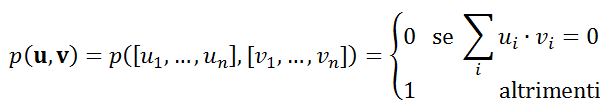
La funzione p avrà valore zero se la sommatoria dei prodotti delle componenti omologhe è nulla, altrimenti restituirà 1. Per fare un esempio: consideriamo i numeri decimali 13 e 6 a cui corrispondono rispettivamente le n-ple u=[1,1,0,1] e v=[0,1,1,1]. Essendo u·v=1×0+1×1+0×1+1×1=2≠0, si avrà p(u,v)=1.

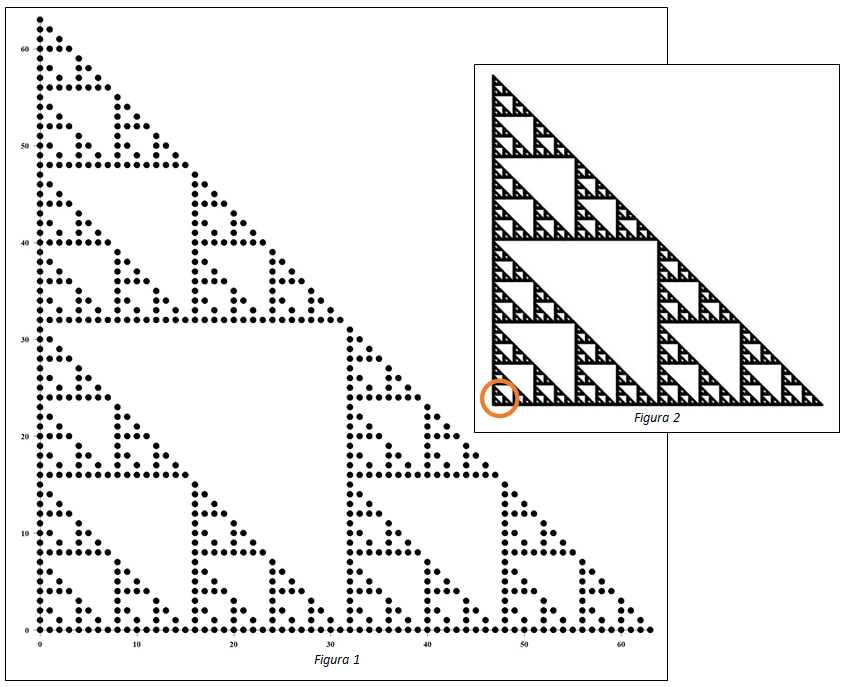
Considerando tutti i numeri decimali tra 0 e 2⁶–1 ossia tra 0 e 63, possiamo per ogni coppia (a,b) con {0≤a≤63, 0≤b≤ 63} calcolare p(u,v), dove u e v sono le n-ple binarie corrispondenti ai numeri a e b. Se rappresentiamo su un sistema di assi cartesiani i valori assunti dalla funzione p(u,v), inserendo un punto nella coordinata (a,b) quando funzione p(u,v) vale zero, si ottiene una struttura frattale simile a quella di Sierpinski. Come possiamo notare da un triangolo equilatero con cateto di 64 unità (intera Figura 1) si ottengono tre triangoli con cateto lungo 32 unità (i triangoli aventi l'angolo retto in (0,0), (32,0) e (0,32)) e poi 9 triangoli con cateto di 16 unità e così via fino a giungere ad una figura composta da 3⁴=81 triangoli con un cateto di dimensione 4 unità. La dimensione frattale resta quella di Sierpinski ossia D=(log⁡(3))⁄(log⁡(2)). Notiamo che l'esponente 4, trovato nell'esempio, indica il numero di dimezzamenti effettuati per giungere al triangolo più piccolo. Una struttura così definita, all'infinito, genera un frattale composto da infiniti blocchi autosimili. Un esempio lo si può avere osservando la Figura 2 generata prendendo in considerazione la tavola dei prodotti di tutti i numeri interi fino a 2¹⁰–1=1023. La struttura generata è simile alla precedente, infatti basta osservare che la parte di frattale evidenziata in Figura 2 corrisponde al frattale di Figura 1.

1. Nei tre esempi visti in precedenza otteniamo le dimensioni frattali sono: log(N)/log(N)=1, log(N²)/log(N)=2, log(N³)/log(N)=3, rispettivamente per i segmenti, i quadrati e i cubi.