Dr. Geo e la Geometria tolemaica

INTRODUZIONE
L'uso di software per la manipolazione dinamica di oggetti geometrici costituisce, da lungo tempo, un ausilio essenziale nella didattica della Geometria. I motivi sono stati spesso evidenziati: attraverso il software è possibile realizzare costruzioni geometriche molto accurate e modificarle dinamicamente, raggiungendo un alto grado di visualizzazione nei diversi contesti in cui si opera. In questo modo si riesce a conferire, anche ad argomenti usualmente ostici come lo studio dell'azione delle trasformazioni geometriche, una maggiore incisività e chiarezza. Allo stesso tempo, l'uso del software offre allo studente diverse occasioni formative che vanno dalla sperimentazione di situazioni geometriche nuove, alla verifica empirica della validità o meno di proposizioni, alla riproduzione di dimostrazioni costruttive e, in casi fortunati, alla formulazione di congetture che portano a nuovi risultati.
Normalmente lo studio della Geometria (con l'ausilio di programmi interattivi) e quello dei fondamenti della programmazione vengono affrontati in modo separato e, particolarmente il secondo, in una fase avanzata del curricolo. Non mancano tuttavia interessanti eccezioni in questo senso, come ad esempio l'utilizzo del Logo nella scuola elementare. Attraverso l'uso del Logo, si apprende facilmente ad associare le istruzioni del linguaggio all'accadere di fatti geometrici su un foglio di lavoro. Tornando ai programmi di Geometria interattiva, spésso essi tendono come approccio generale ad offrire molte funzionalità, senza preoccuparsi di costruire ambienti di apprendimento intelligenti, che sollecitino l'utilizzatore a costruirsene di nuove.
Nell'ampio panorama di programmi dedicati allo studio della geometria interattiva si differenzia Dr. Geo. Questo è un programma open source, ossia liberamente distribuito con il codice sorgente (http://www.ofset.org/drgeo), sviluppato da H. Fernandes dell'associazione francese Ofset (Organization for Free Software in Education and Teaching), che funziona in ambiente Linux. Al suo interno, Dr. Geo ospita un semplice ambiente di programmazione in linguaggio Guile, che permette di interagire con l'apparato di funzionalità geometriche tipiche di tutti i software di Geometria interattiva.
In questo breve articolo, per mostrare le potenzialità di Dr. Geo, si analizzano alcune situazioni geometriche prese dall'Almagesto di Tolomeo. Questa scelta particolare è dettata anche dal desiderio di invogliare i lettori ad approfondire la conoscenza dell'opera tolemaica, eventualmente prendendo visione della notevole traduzione inglese di J. Toomer [1]. Contrariamente a quanto spesso si crede, infatti, l'Almagesto non è un libro di Filosofia, ma una grande opera scientifica, di Matematica applicata allo studio dei moti planetari. Da questo punto di vista, il suo titolo greco originale Mathematike Syntaxis (Raccolta Matematica) è più fedele ai contenuti dell'usuale appellativo Almagesto La Grande ad essa conferito dagli astronomi arabi.

I PENTAGONO E DECAGONO
Nel libro I, capitolo decimo, dell'Almagesto [1] vengono esposte le considerazioni geometriche che portano alla costruzione della tavola delle corde che verrà poi esposta nel capitolo undicesimo. Quanto contenuto in questo capitolo potrebbe essere integralmente compreso da uno studente di Liceo e potrebbe essere fruttuosamente utilizzato per lo studio della Trigonometria [2]. Qui ci limitiamo ad analizzare i contenuti dei primi due teoremi, di cui il secondo è noto come teorema di Tolomeo.
La brevissima introduzione all'argomento, che Tolomeo appone all'inizio del capitolo, è stilisticamente molto vicina a quanto si ritrova nella letteratura matematica contemporanea. Oltre ad alcuni dettagli tecnici, si dice che per quanto verrà trattato nel seguito si ha bisogno di una tavola delle corde e che, per determinarla rigorosamente, è necessario rifarsi ad alcuni teoremi geometrici. Immediatamente dopo, Tolomeo enuncia e dimostra, con riferimento alla figura 1, il seguente teorema.

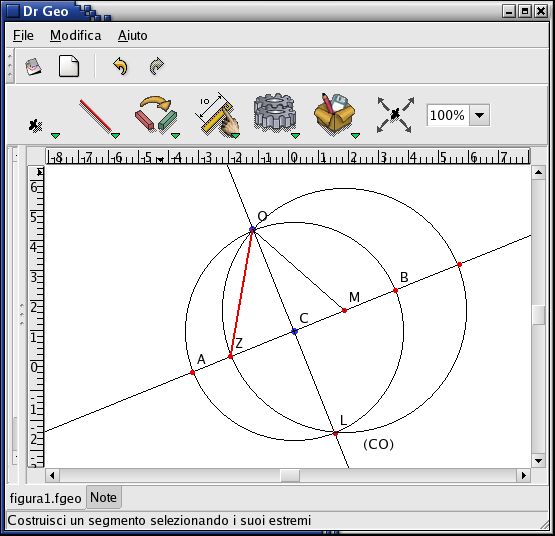
Teorema 1 Sia ABO la circonferenza di diametro AB e centro C e sia LO il diametro perpendicolare ad AB. Detto M il punto medio del raggio CB, si consideri il punto Z appartenente ad AB e tale che MZ = M0. Allora OZ è uguale al lato del pentagono regolare inscritto nella circonferenza ABO e CZ è uguale al lato del decagono regolare inscritto nella stessa circonferenza.

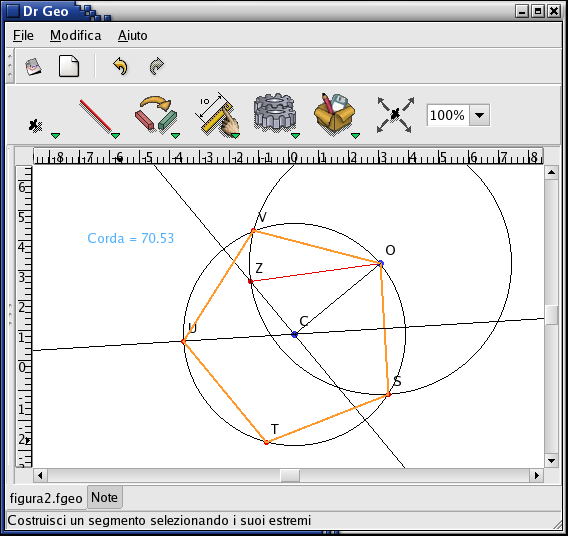
La dimostrazione del teorema richiede conoscenze approfondite di alcuni teoremi di Geometria euclidea e per essa si rimanda direttamente all'Almagesto. Utilizziamo invece Dr. Geo per costruire, a partire dal teorema precedente, il pentagono regolare inscritto in ABO e per salvare in una macro costruzione questa costruzione, che non appartiene alle costruzioni base offerte dal programma, per eventuali usi futuri. Le costruzione del pentagono è rappresentata in figura 2.

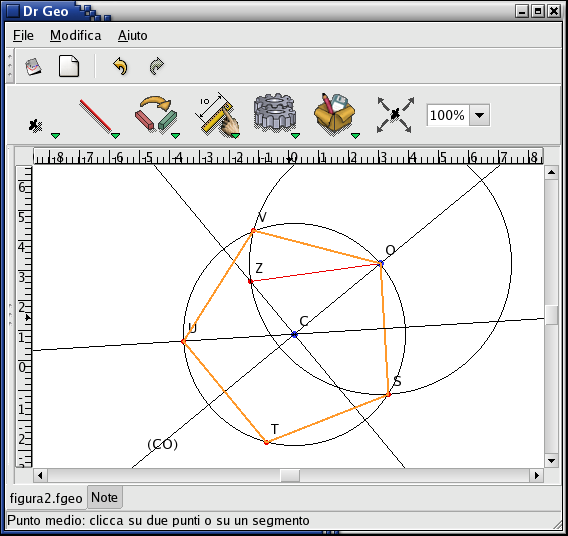
La creazione di macro in Dr. Geo è completamente guidata. Per costruire, ad esempio, il pentagono inscritto in una circonferenza a partire dalla costruzione tolemaica, è sufficiente specificare come parametri di ingresso i punti C e O, come parametri di uscita lati e vertici del pentagono e assegnare nome e descrizione della macro.
Dopo aver enunciato e dimostrato il teorema precedente, Tolomeo calcola il valore delle corde relative agli angoli di 36° e di 72° ottenendo i valori:

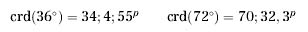
che si riferiscono ad una circonferenza di raggio 60. La strana scrittura dei risultati, tipica dell'Almagesto, si può trasformare agevolmente in una scrittura decimale. Se ad esempio consideriamo il caso della corda dell'angolo di 72°, otteniamo:

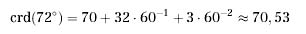
Risulta interessante confrontare questo valore con il valore calcolato da Dr. Geo. Per farlo, è necessario riportare il valore direttamente calcolato, attraverso il righello di Dr. Geo, al caso di una circonferenza di raggio 60 calcolando:

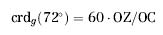
dove il pedice g indica che il calcolo è fatto in Dr. Geo. Data la semplicità del calcolo, potremo azionare una calcolatrice ed eseguirlo direttamente. Tuttavia, come anticipazione, vediamo in che modo calcolare questo valore utilizzando uno script in Guile. Per progettare lo script, dobbiamo aver chiaro che ci servono dati relativamente a due oggetti geometrici: vale a dire i segmenti OZ (variabile a1) e OC (variabile a2). Azioniamo allora l'utilità script in Dr. Geo e subito dopo cucchiamo con il mouse nell'ordine, prima su OZ e poi su OC. A questo punto, cucchiamo in un punto dello schermo dove vogliamo far comparire il risultato dello script. Ci apparirà allora la scritta Dr. Genius. Possiamo ora procedere ad editare lo script: dopo aver selezionato il tasto proprietà e cliccato sulla scritta, si apre una finestra dove possiamo scrivere il seguente codice in Guile

Nella prima linea si definisce OZ, assegnando il valore numerico ottenuto prendendo la lunghezza dell'oggetto geometrico a1, corrispondente al primo clic del mouse; quindi, si definisce OC prendendo la lunghezza dell'oggetto geometrico a2, corrispondente al secondo clic del mouse, e infine si calcola l'espressione. Le operazioni vengono rappresentate come funzioni. Sullo schermo, vedi figura 3, viene visualizzato il valore 70.53 corrispondente a quello tolemaico.

TEOREMA DI TOLOMEO
Il capitolo decimo dell'Almagesto prosegue con l'enunciato e la dimostrazione del celebrato teorema di Tolomeo. Il teorema prende questo nome in quanto non si hanno documenti anteriori all'Almagesto in cui esso sia contenuto. Tuttavia è stato avanzato il dubbio che un teorema simile potesse essere contenuto in un opera di Menelao [2].

Teorema 2 (di Tolomeo) Sia ABCD un qualsiasi quadrilatero inscritto in una circonferenza. Allora la somma dei prodotti dei lati opposti è uguale al prodotto delle diagonali, ossia:

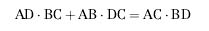
Dimostrazione Costruiamo innanzitutto il segmento DE in modo che LADE=LBDC. I triangoli ADE e DCB sono simili in quanto LADE = LBDC (per costruzione) e LDAE = LDBC perché insistono entrambi sulla corda DC. Allora:

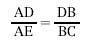
da cui AD•BC = AE•DB. Inoltre i triangoli ABD e DEC sono simili in quanto LABD=LECD, perché insistono entrambi sulla corda AD, e LADB=LEDC in quanto somma di angoli uguali. Allora, anche:

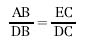
da cui AB•DC = EC•DB.

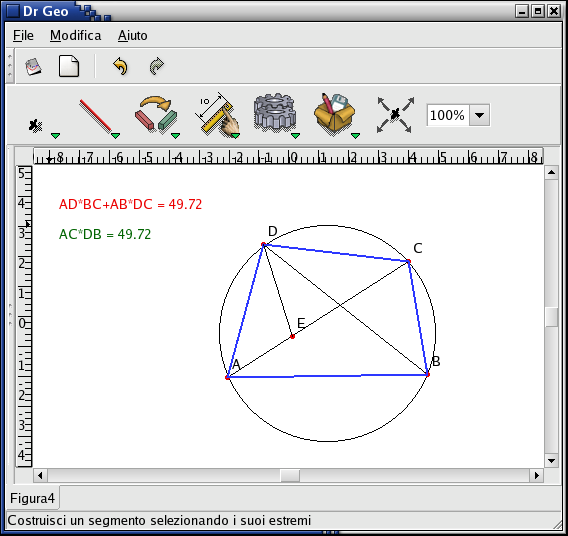
Sommando membro, a membro si ha AD•BC+AB•DC=AE•DB+EC•DB, da cui la tesi. La dimostrazione tolemaica è semplice. Tuttavia vogliamo mostrare come, attraverso Dr. Geo, si possa verificare empiricamente la sua validità. Naturalmente Dr. Geo può solo verificare, nel limite di errori di approssimazione, la validità della relazione precedente, anche se ciò non costituisce una dimostrazione! Tuttavia, vedremo subito che questo tipo di indagini hanno un'utilità didattica non trascurabile. Per verificare il teorema, possiamo scrivere due script in Guile - la sintassi è identica a quella dello script precedente - uno per ogni membro della relazione del teorema di Tolomeo. Noteremo che in effetti i risultati di uscita degli script sono identici (vedi figura 4) e tali rimangono anche se si manipola dinamicamente la costruzione geometrica, almeno fino a quando il poligono si mantiene convesso. Quando il poligono perde la convessità, il teorema non è più valido e questo Dr.Geo ce lo notifica con chiarezza in figura 5.

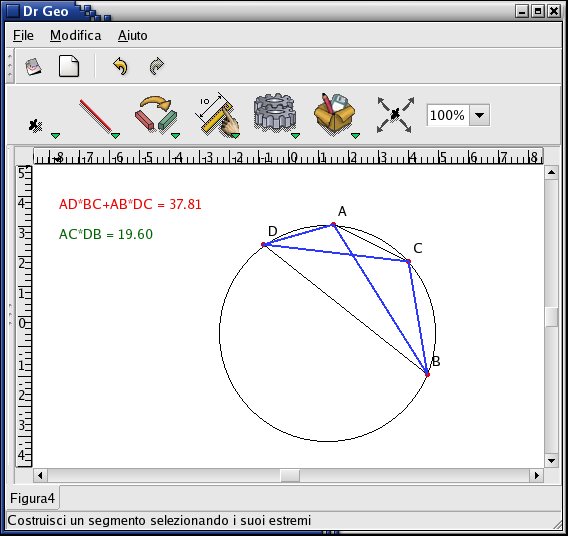
Attraverso il software, siamo quindi riusciti a scoprire che nell'enunciato del teorema manca la precisazione del fatto che il quadrilatero deve essere convesso.

BIBLIOGRAFIA
[1] J. Toomer, Ptolemy's Almagest, Princeton University Press, Princeton, 1998.
[2] C. Boyer, Storia della Matematica, Mondadori, Milano, 1980.

LETTURA CONSIGLIATA
A. Centomo, H. Fernandes, Manuale di Dottor Geo, disponibile nell'area Documentation, al sito http://ww.ofset.org/drgeo/