E se (ri)partissimo a giocare (anche) da Euclide?

Occupandomi, oramai prevalentemente, di problemi che riguardano l’insegnamento della Matematica, a vari livelli scolastici, mi sono trovata spesso a chiedermi come mai si impara a giocare (a giochi diversi, commisurati alle differenti età) e non si impara a... giocare alla Matematica.

Non intendo i giochi matematici che sono senz’altro utili, divertenti ed appassionanti (e che per questo svolgono un ruolo meritorio per la diffusione e la familiarizzazione con la Matematica, il Centro Pristem docet… in tal senso) quanto proprio la Matematica, o meglio porzioni di essa (quelle presentate o presentabili come teorie assiomatiche) che possono essere interpretate come giochi. Molte sono infatti le analogie tra i due contesti (naturalmente il tutto va preso cum grano salis).

Prendiamo ad esempio un gioco semplice come quello della dama: le pedine possono essere viste come termini primitivi, le dame come termini definiti, le posizioni iniziali come gli assiomi, le regole del gioco (ad esempio il muoversi in diagonale) come regole di deduzione e cosa siano le posizioni finali... lo lascio al lettore.

Andando avanti in questo modo, potremo vedere l’analogia tra un gioco più complicato come quello degli scacchi (cosa rappresenta lo scacco matto?) o più semplice, come quello del Lego.

Perché quindi un bambino (od un adulto) non ha difficoltà ad imparare un gioco adatto alla propria età (o esperienza o livello) e si cimenta quasi subito con una partita (anzi non vede proprio l’ora di iniziare) e invece con la Matematica questo non succede praticamente mai (se non in chi diventerà un matematico di professione o giù di li), tanto che la maggior parte degli studenti non riuscirà mai non solo a portare a termine una partita ma neppure proverà a cimentarsi con una?

Non è che per caso spesso non sono chiare o bene esplicitate (almeno una volta nel curriculum scolastico) tutte le componenti del gioco? Non è che spesso noi docenti le diamo per scontate (tanto si capisce dal contesto, ma quale?) o non le diamo consapevolmente (magari per ragioni anche plausibili: il poco tempo, i programmi da rispettare ecc ecc), o non ci accorgiamo di non darle (e quindi la scelta è inconsapevole)? E se per una volta provassimo a darle per intero? E come esempio (ri)partissimo proprio dagli Elementi di Euclide?

Certo è un esempio per alcuni versi… controcorrente. Gli Elementi sono un’opera di sistematizzazione di risultati precedenti in cui manca del tutto il cammino che ha portato a questi risultati, non vi è spazio per l’intuizione, il legame con la realtà volutamente non c’è. Non è neanche tra gli esempi più facili e si potrebbero (o dovrebbero) quindi cercare esempi più accattivanti ma sull’altro piano della bilancia ci sono delle motivazioni che ci fanno (pro)pendere per questa scelta, ad esempio il pensiero di Poincaré: “La tâche de l’educateur est de faire repasser l’esprit de l’enfant par où a passé celui de ces pères, en passant rapidement par certaines étapes mais en n’en supprimant aucune. A ce compte, l’histoire de la science doit ètre notre guide.” (Poincaré, 1899).

Oltre a questa motivazione che potremo definire storico/pedagogica ci sono altre motivazioni, ad esempio logico/fondazionali/filosofiche (che possono suggerire percorsi interdisciplinari), algebrico/geometriche (che possono suggerire percorsi intradisciplinari) dove l’interesse più propriamente didattico (nel senso di implementazione sul campo) potrebbe permeare, nel senso di essere trasversale a, tutti questi aspetti.

Proveremo ad accennare a qualcuno di questi percorsi lasciandone altri per un eventuale nuovo contributo. Anticipiamo che non si tratta di “infliggere” la lettura degli Elementi agli studenti, operazione che risulterebbe secondo Odifreddi (2003) un “pericoloso anacronismo” rischiando di provocare un “deleterio effetto”, quanto di prendere spunto da quest’opera (in qualche modo paradigmatica) per confrontare ad esempio le regole del gioco di allora con quelle attuali (e di come il cambio delle regole possa rendere le partite più o meno lunghe o più o meno facili). Questa operazione può contribuire a far vedere come in realtà la matematica sia una disciplina dinamica più di quanto risulti nell’immaginario collettivo, caratterizzata sia da scelte e decisioni (più o meno vincenti) che hanno risentito di influenze varie (ad esempio filosofiche) che da errori, omissioni e approssimazioni (vedi lacune nell’opera euclidea, alcune delle quali hanno richiesto più di 2000 anni di storia per essere adeguatamente colmate).

Definizioni esclusive e non inclusive

Merita ad esempio osservare che per Euclide il triangolo isoscele (= con gambe uguali) è quello che ha soltanto(!) due lati uguali, per cui un triangolo equilatero non è isoscele.

Anche il quadrato per Euclide non è un particolare rettangolo, in quanto il rettangolo non ha tutti i lati uguali. Non è un caso che Aristotele, nella Metafisica, inserisca nella lista pitagorica dei contrari la coppia “rettangolo-quadrato”, considerandoli termini antitetici tra di loro.

Anche quella di operare ora con definizioni inclusive (cioè dal generale al particolare), e non esclusive, è una scelta; ma ne siano consapevoli e ne rendiamo consapevoli gli studenti? Ne siamo ad esempio consapevoli quando correggiamo gli studenti che ragionano invece alla… Euclide?

“In Euclide i triangoli equilateri non sono isosceli, i quadrati non sono rettangoli ne’ rombi, e nessuno dei precedenti è un parallelogramma, mentre ora consideriamo i triangoli equilateri come particolari triangoli isosceli, i quadrati come particolari rettangoli e rombi, ed i precedenti come parallelogrammi. Nel linguaggio ordinario si usa la vecchia terminologia euclidea (…). C’è un buon motivo perché i geometri ed i matematici agiscano differentemente. La maggior parte delle proprietà, e le più importanti, sui rettangoli [con i lati disuguali] sono godute anche dai quadrati, e questo ci dispensa dal doverle dimostrare di nuovo per i quadrati. Dire di un quadrato che è un rettangolo è dire una verità ma non tutta la verità come invece un testimone è chiamato a fare in sede di giudizio. Distinguere tra la verità e tutta la verità, e richiamare ciò in ogni momento con più o meno evidenza a seconda della necessità, è un importante principio logico globale, che è implicito per una gran parte della matematica. Gli insegnanti probabilmente dicono agli studenti che, a differenza del linguaggio ordinario, in geometria si trattano i quadrati come fossero rettangoli e rombi, ma toccano con gli studenti la questione del perché di questo? O anche peggio, si pongono loro stessi la questione e sono consapevoli del principio generale di dire la verità e tutta la verità?” (Freudenthal, 1989).

Sulla necessità della dimostrazione

Τὸ δ’ὅτι διαφέρει και τὸ διότι ἐπίστασθαι

Il sapere che differisce dal sapere perché

(Aristotele, Analitici Posteriori I, 13)

Proclo [412-485 d.C.] nel suo Commento al I libro degli Elementi di Euclide riferisce che gli Epicurei irridevano il teorema (“In ogni triangolo la somma di due lati è maggiore del lato rimanente”, Proposizione XX del I libro) perché è evidente, anche ad un asino, che se si fosse posto del foraggio in un vertice del triangolo e l’asino ad un altro vertice, l’animale (avido di cibo), avrebbe percorso un solo lato e non due. Proclo stesso replica a questa osservazione dicendo che “la mera percezione della verità di un teorema è cosa differente da una dimostrazione scientifica di esso e dalla conoscenza del motivo per cui è vero”. E se poi la percezione ci ingannasse?

Situazione paradossale

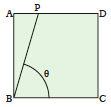
Se l'arco AB è uguale all'arco CD l'area delle due strisce è la stessa?

[La risposta si trova nel I libro di Euclide, Proposizione XXXVI, conseguenza della PXXXV che è alla base del calcolo dell'area di un parallelogramma]

Sui paradossi visivi

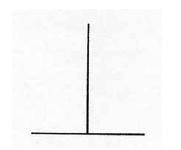
Una lunga serie di paradossi visivi (alcuni bene illustrati in questa rivista nella rubrica Illusioni) mostra efficacemente la tensione tra le percezioni pratiche e le aspettative teoriche, a partire dalla valutazione delle lunghezze. Riportiamo altri esempi, alcuni presenti nel libro “C’è spazio per tutti” di P. Odifreddi. Partiamo dall’esempio del 1851 di Adolf Fick per cui un segmento interrotto appare decisamente più corto di uno della stessa lunghezza che lo interrompe.

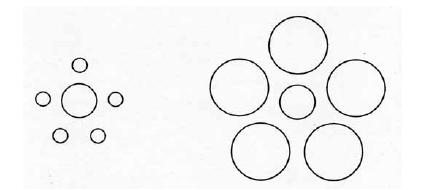
Che la valutazione delle grandezze dipenda fortemente dai riferimenti e testimoniato dall’illusione del 1897 di Theodor Lipps, per cui uno stesso cerchio appare più piccolo se circondato da cerchi grandi e più grande se circondato da cerchi piccoli.

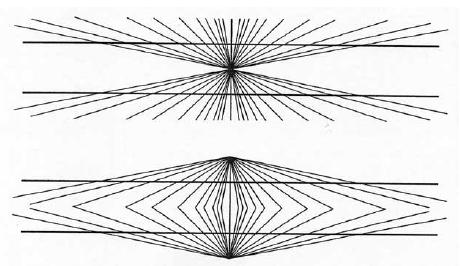
L’arte ottica ha sfruttato sistematicamente questo genere di illusioni e i trucchi più efficaci riguardano l’inganno del parallelismo (esempio di Ewald Hering del 1861 e di Wilhelm Wundt del 1896).

Sostituendo alle rette parallele dei cerchi concentrici e al fascio di rette un fascio di curve passanti per il centro, si ottiene la sorprendente spirale di James Fraser del 1908 (controllare con un dito o una matita che ci sono soltanto cerchi).

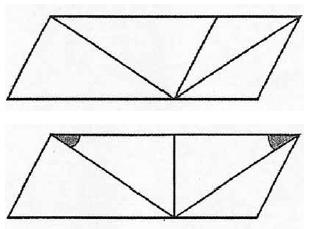
Altro esempio interessante, attribuito a Friedrich Sander, è quello di un triangolo isoscele, che visto nel contesto di due parallelogrammi diversi, viene percepito come scaleno (Gario, 2010).

Interazione filosofia-matematica: Platone

Vediamo ora quanto l’opera euclidea sia stata influenzata dalle posizioni filosofiche del tempo. Platone (427-347 a.C.) si interessava della natura degli oggetti matematici e cercava di spiegare ad esempio che cosa sono le figure di cui si tratta in geometria. La sua posizione è: le figure geometriche sono le idealizzazioni o idee (non a caso “idea” deriva dal termine greco ειδοσ che significa “forma”, “figura”) degli oggetti fisici che percepiamo attraverso le sensazioni.

Poiché le idealizzazioni posseggono una perfezione che gli oggetti fisici non hanno, esse non solo esistono indipendentemente da questi, e costituiscono un mondo parallelo a quello sensoriale, ma sono addirittura la vera realtà di cui il mondo sensibile è solo una pallida immagine, un mondo di ombre percepite sulle pareti di una caverna (Odifreddi, 2003). La Geometria diventa il modo attraverso il quale veniamo a conoscenza del mondo delle idee e come tale acquista un ruolo fondamentale, cosi come nell’opera euclidea. Come in Platone, anche negli Elementi troviamo che la costruzione con riga e compasso (ma qual e il compasso di Euclide?) rivestirà un ruolo centrale (come regola del gioco in qualche modo privilegiata).

Platone, a differenza di Aristotele, non sottolinea invece il ruolo della deduzione. Essa può soltanto rendere esplicito quello che è già vero indipendentemente. In particolare, la correttezza di un teorema non deriva certo dalla correttezza della dimostrazione bensì dal fatto che descrive una situazione di fatto (Odifreddi, 2003).

Interazione filosofia-matematica: Aristotele

L’atteggiamento precedente cambia con Aristotele (384-322 a.C.) che si interessa più alla natura del metodo matematico. Sia nell’Organon che nella Metafisica egli sistematizza la Logica come scienza del ragionamento dicendo chiaramente che le leggi della Logica sono si formalizzate sul modello delle dimostrazioni matematiche ma anche che la Logica deve essere considerata indipendentemente dalla Matematica e ad essa precedente (Odifreddi, 2003). In particolare la deduzione è l’unico modo di stabilire la verità di un enunciato matematico. Per quanto riguarda questo aspetto, Euclide

- distingue assunzioni (proposizioni primitive non dimostrate) da teoremi (proposizioni via via più complesse dimostrate a partire dalle assunzioni) e in ciò segue Aristotele il quale afferma nella Metafisica che “non tutto può essere dimostrato, perché questo porterebbe ad un regresso infinito”;

- separa logica da Matematica: lo si vede dal fatto che le assunzioni sono divise in nozioni comuni (κοιναὶ ἒννοιαι) e postulati matematici (αἰτήματα); anche Aristotele infatti distingue verità comuni a tutte le scienze deduttive da quelle proprie di una particolare scienza (nel caso di Euclide, la Geometria); al giorno d’oggi si tende a non fare più questa distinzione, usando in entrambi i casi il termine assioma (da axios, degno di fede, mentre postulato significa richiesto di fede); qualche volta si chiamano le prime assiomi logici;

- da poi pochi postulati, solo 5, sempre in accordo con Aristotele il quale nella Metafisica afferma che “le scienze basate su poche assunzioni sono le più esatte”;

- da infine poche nozioni comuni (solo 5, anche se non c’e concordanza tra gli storici su questo numero) una delle quali, la terza che afferma che “se da cose uguali sono sottratte cose uguali, i resti sono uguali”, era stata citata proprio da Aristotele come esempio di verità logica.

In che cosa invece Euclide non segue (o non sembra seguire) Aristotele? Euclide non separa (o non sembra separare) le nozioni definite da quelle non definite cioè i termini primitivi (ad esempio le nozioni di punto e linea). Aristotele critica esplicitamente questo tipo di definizioni, in quanto afferma che è compito dei postulati e degli assiomi enunciare le proprietà essenziali delle nozioni primitive. Questo punto delicato – se per Euclide veramente la nozione di punto è da considerarsi definita – sarà oggetto di riflessioni e considerazioni future.

Necessità dei termini primitivi

Sulle definizioni

Il primo dei 13 libri degli Elementi di Euclide inizia, prima ancora che con i 5 postulati e le 5 nozioni comuni, con 23 ὃροι. Gli ὃροι sono i termini, o definizioni, che saranno presenti in questo come in altri libri degli Elementi. Le prime definizioni del I libro sono descrizioni e caratterizzazioni di enti con i quali opera il geometra (punto, linea, superficie, ...).

La prima, per certi versi più famosa e controversa, definizione è quella di punto: Punto è ciò che non ha parti (Σημεῖόν ἐστιν οὗ μέρος οὐθέν).

Perché viene cosi messa in discussione? Oltre che per il suo carattere un po’ oscuro, viene criticata perché se il punto è un termine primitivo, non deve essere definito e, se invece è un termine definito, la definizione lo deve introdurre a partire da una combinazione di termini della teoria già dati (o perche primitivi o perche definiti precedentemente). Ma il punto e il primo termine della lista. Euclide era un matematico cosi sprovveduto o forse c’è una motivazione alla base di questa sua scelta?

Per una (possibile) risposta cosi come per la descrizione delle regole del gioco euclideo (abbiamo finora accennato solo alle pedine), si dovrà aspettare il prossimo foglio con le istruzioni, chissà forse un prossimo numero della rivista, fermo restando che “Il vero viaggio di scoperta non consiste nel cercare nuove terre, ma nell’avere nuovi occhi” (Marcel Proust). 

Bibliografia

• Freudenthal H., Logic as a subject or as an attitude? in Barra M., Zanardo A. (a cura di): Atti del XII incontro di Logica Matematica: La logica matematica nella didattica

(Roma, 6-9 aprile 1988), Siena, Scuola di specializzazione in Logica matematica, Universita di Siena, 1989, 27-38.

• Gario P., Perche dimostrare cio che e evidente, L’insegnamento della matematica e delle scienze integrate, 33(2), 2010, 171-195.

• Odifreddi P., Divertimento geometrico, Bollati Boringhieri, Torino, 2003

• Odifreddi P., C’è spazio per tutti, Mondadori, MI, 2010

• Poincare H., La logique et l’intuition dans la science mathematique e dans l’enseignement, L’enseignement mathematique, 1899, 157-162.