Eulero: genio, pensatore, maestro

INTRODUZIONE

NON C'È MATEMATICO CHE, dal Settecento ad oggi, abbia omesso di riconoscere i meriti di Eulero: Pierre Simon de Laplace (1749-1827) ripeteva ai propri allievi: 'Lisez Euler; c'est notre mailre à tous!" e il grande Cari Friedrich Gauss (1777-1855) affermò che "Lo studio delle opere di Euler rimane la miglior scuola nei diversi campi delta matematica e non può essere rimpiazzato da nient 'altro" [1]. L'astronomo François Arago (1786-1853) definÌ Eulero "l'incarnazione dell'Analisi" e la collezione di citazioni potrebbe continuare [2].

Ma Eulero non fu solo il genio assoluto dell'Analisi matematica: fu anche un grande appassionato e un vero maestro. Le euleriane Lettere a una principessa d'Alemagna, ad esempio, come vedremo, riassumono il vero e proprio corso per corrispondenza "sopra diversi soggetti di fisica e filosofia", come appare dal frontespizio della prima edizione italiana, pubblicata da Terres a Napoli nel 1787 (curata dall'abate Oronzo Carnevale, una delle prime traduzioni dell'opera originale in francese edita tra il 1768 e il 1772). In questo contributo presenteremo alcuni spunti culturalmente vivaci tratti dalle opere euleriane. Inizieremo approfittando di un quesito tratto dai giochi matematici di Martin Gardner, per passare poi a considerare alcuni spunti originali tratti dalle Lettere ora citate e da altri lavori.

Eulero

ALLA RICERCA DI NUMERI PRIMI

GARDNER, inesauribile ricercatore di curiosità e Creatore di giochi matematici, ci domanda: si consideri inizialmente il nnmero (primo) 41; ad esso si aggiunga 2, ottenendo così 43, un altro primo; a quest'ultimo aggiungiamo 4, ottenendo 47, primo: ad esso aggiungiamo 6 e il risultato sarà 53, ancora primo. Ebbene, andando avanti così troveremo sempre dei primi o no [3]?

Prima di proseguire invitiamo il lettore a ... pensarci un po'. Si tenga sin d'ora presente che la ricerca di formule in grado di fornire numeri primi ha impegnato molti matematici nella storia della nostra disciplina. Un tentativo elementare in tale direzione può essere la ricerca di formule polinomiali a coefficienti interi P(x) in grado di assumere valori primi per x intero, eventualmente soggetto ad oppoltune condizioni. Sappiamo oggi però che un primo basilare risultato da coosiderare a tale proposito è negativo: è infatti noto che formule di questo genere non possono portare a valori primi per ogni intero; se P(x) è un polinomio non costante con coefficienti interi nella sola incognita x, esistono infiniti interi x tali che P(x) non è primo. Si prova inoltre che se f(x) è un polinomio a coefficienti complessi in più indeterminate, tale che i valori da esso assunti per valori natutali di esse siano primi (in valore assoluto), allora f(x) deve essere costante[4].

Torniamo ora al quesito precedente. Si tra.tta dunque di valutare se:

sono "tutti" numeri primi. Chiaramente il problema riguarda quel "tutti": anche gli studenti più giovani sanno che i pochi numeri ora riportati, 41, 43, 47, 53 e 61 sono primi. Ma ... proseguendo cosi? Il risultato limitativo sopra segnalato ci mette in guardia: è molto difficile trovare delle formule "semplici" in grado di fornire esclusivamente primi, e in alcuni casi si può addirittura dimostrare che una tale ricerca è destinata. all'insuccesso. Ma la procedura sopra presentata non ha, almeno per ora, l'aspetto di una formula polinomiale a coefficienti interi e dunque merita dì essere esaminata.
Per rispondere alla domanda di Gardner notiamo che il numero ottenibile operando nel modo ora suggerito ha la forma:

dove la sommatoria ci riporta al problema del "giovane
"Gauss". Uno tra i più diffusi aneddoti storico-matematici ricorda che Gauss, ancora fanciullo, calcolò la somma dei primi n numeri naturali (nel caso, si narra, di n=100) utilizzando un procedimento riassumibile nello schema seguente:

Sopra la riga si trovano due volte tutti i numeri da 1 a n. Sotto la riga si trovano le somme di tali numeri a due a due: e sono n volte n+1. Pertanto:

Inseriamo questo risultato nella precedente espressione di
x(n):

Dunque i numeri ottenibili con il procedimento proposto sono dati da:

x(n)=n²+n+41

Già il fatto che questa sia una formula polinomiale dovrebbe far scattare il "semaforo rosso" che abbiamo ricordato. Ma per renderci conto che non tutti i valori assunti da n²+n+41 sono primi non è necessario scomodare sofisticati risultati di Teoria dei numeri. Basta osservare che per n=40 si ottiene:

x(40)=40²+40+41=40·(40+1)+41

e questo numero è divisibile per 41 (anzi, è 41²; tutto ciò appare a colpo d'occhio, ma si verifica che n²+n+41 è composto anche per altri valori: per n=44 si ha 2021=43^.47, per n=49 si ha 2491= 47·53 ecc.).
Dunque la risposta al quesito di Gardner è negativa. Ma questo non significa che il polinomio n²+n+41 non sia molto interessante. Esso infatti assume valori primi per n intero con 0≤n≤39;

41. 43. 47, 53, 61,71,83,97, 113, 131, 151,173, 197, 223, 251,281,313, 347,383, 421, 461, 503, 547, 593, 641, 691. 743,797,853, 911, 971, 1033. 1097,1163,1231, 1301, 1373,1447,1 523.1601,

Fu proprio Eulero nel 1772 a segnalare tale proprietà, oggi ripresa in innumerevoli varianti (si pensi alla spirale dei primi attribuita a Stanislaw Ulam) [5]. E l'interesse del grande matematico di Basilea per le folmule polinomiali lo spinse a segualare la presenza di altre formule interessanti, come x²+x+17 che porta a valori primi per x = 0, .... 15.

L'osservazione etuleriana può essere generalizzata e fornire spunti anche didatticamente interessanti: quali polinomi del tipo x²+x+q, con q primo, portano a valori primi per x=0,1, .... q-2? Inoltre, può verificarsi ciò per polinomi quadratici a coefficienti interi diversi da quelli considerati?
Per quanto concerne la prima questione, si dimostra che i polinomi della fonna x²+x+q, con q numero primo assumono valori primi per x = 0, 1...., q -2 se e solo se q assume uno dei valori 2, 3, 5, 11. 17. 41 [6]. Ciò dunque conferma che Eulero ha centrato il bersaglio importante: ha individuato il polinomio della forma x² + x + q "prolifico" in assoluto, cioè quello che assume il maggior numero iniziale di valori primi.
Per quanto riguarda la seconda questione, una lunga riflessione coinvolge procedimenti e concetti superiori (le ricerche risalgono a Dirichlet. dal 1839 al 1840) [7]; può essere tuttavia stimolante, anche dal punto di vista didattico, affrontare alcune questioni limitandosi all'uso di tecniche elementari.
Consideriamo i polinomi Qa,p(x)=ah²+ah+p e i sottainsiemi di N:

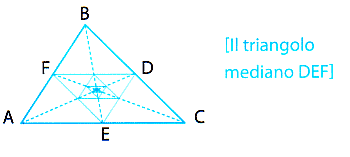
Alcuni di essi sono costituiti esclusivamente da numeri primi. Ad esempio. Ribenboim (8] elenca le coppie:

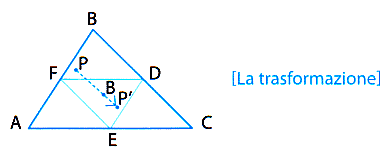
Sì possono fare inoltre le seguenti elementari constatali riguardanti gli insiemi I(a ; p), piccole dimostrazioni alla portata degli allievi della scuola secondaria:
• se p|a, I (a; p) non è costituito esclusivamente da primi
Infatti se pIa scriviamo a=kp (con k naturale non nullo) e risulta; m(h)=ah²+ah+p=kph²+kph+p=P(kh'+kh+1)
• Se q≥5 è primo, I[(q -3)/2,3] è costituito escIusivamente da primi.
Infatti se q≥5 è primo, I[(q -3)/2. 3]=(3; q).
• Per ogni scelta di p, I(6; p) non è costituito solamente da numeri primi. Lasciamo la verifica diretta al lettore [9].

Quanto ora visto testimonia. dunque che l'eredità di Eulero può essere interessante anche per gli insegnanti di oggi.
Ma c'è di più: Euero fu un vero maestro, con la gioia di fare Matematica e di comunicarla. Il diciannovenne JosepbLouis Lagrange (17361813) ad esempio. appena nominato professore alla Scuola d'Artiglieria di Torino, trovò in Eulero un corrispondente attento e prezioso (a lui comunicò le sue idee relative al Calcolo delle variazioni), tanto che lo stesso Eulero, quattro anni dopo. sostenne la candidatura del giovane matematico per l'elezione all' Accademia di Berlino (a trent'anni, su proposta dello stesso Eulero e di d'Alembert,

Lagrange sarà nominato da Federico Il di Prussia Presidente della classe di scienze di tale Accademia).
Tra gli "allievi" di Eulero troviamo anche Sophie Friederike Charlotte Leopoldine, figlia del margravio regnante di Brandenburg-Schwedt. futura principessa di Anhalt-Dessau, nipote dello stesso re di Prussia Federico II. La giovane non entrerà nella storia della Matematlca per i suoi risultati, come Lagrange; ma il suo nome, in particolare il suo titolo di "principessa d'Alemagna", è rimasto legato ad una delle opere euleriane più suggestive.

ROVISTANDO NELLE LETTERE: I DIAGRAMMI DI EULERO

LE LETTERE A UNA PRINCIPESSA D'ALEMAGNA risalgono al 1760-1762 e spaziano dalle questioni di Meccanica all' elettricità, dall'Ottica al magnetismo, dalla Geografia all'Astronomia, con frequenti e importanti osservazioni di carattere filosofico (decisamente critiche sia con i newtoniani di stretta osservanza che con gli epigoni, in Germania, della filosofia di Leibniz) [10]. Il tutto scritto con un linguaggio piano e a tratti assai vivace, didatticamente efficacissimo, ricco di esempi chiari e di riferimenti acuti. Ogrti tentativo di riassumere il contenuto di queste celebri Lettere euleriane farebbe torto ad un'opera interessante e profonda. Basti ricordare che proprio in questo libro fecero la loro comparsa i diffusissimi "diagrammi di Eulero", grandi protagonisti della Didattica elementare degli insiemi (le illustrazioni seguenti sono tratte dall'edizione napoletana del1787). Esaminiamo quanto Eulero scrive nella lettera CH (datata 14 febbraio 1761), dopo avere ricordato la classificazione delle proposizioni aristoteliche:

'Per esprimere sensibilmente lo. natura. di queste [...] proposizioni possiam rappresentarle per mezzo difigure. le quali son di un gran soccorso per ispiegare con somma distinzione qual sia l'esattezza di un raziocinio. E poiché una nozione generale contiene un 'infinità di oggetti individuali, si può supporre a guisa di uno spazio, in cui questi oggetti son racchiusi: per esempio sifo/"ma uno spazio perla nozione di uomo (rav. J. fig. 1.) in cui si suppone che tutti gli uomini sien radunati.
Per la nozione di mortale se ne forma un alrro (Tav. l. fig. 2.) dove si suppone che sia compreso quanto vi è di mortale. E quando io pronunzio che tutti gli uomini san mortali, intendo che la prima figura sia contenuta nella seconda. Dunque la rappresentazione di una proposizione universale affermativa sarà quella della Tav. 1. fig. 3., in. cui lo spazio A che denota il soggetto deLla proposizione vien tutto intero racchiuso nello spazio B che è il predicato".

Nella successiva lettera CIll (datata 17 febbraio 1761), Eulero propone di utilizzare le rappresentazioni così introdotte per una riflessione sui sillogismi:

"Questi cerchi o sien questi spazi (imperciocché è indifferente qualunque figura lor si dia) son molto a portata per facilitare le nostre riflessioni sopra questa materia, e per metterci in chiaro qunti misteri la logica si vanta di avere, i quali sommo pena han costata per poterli dimostrare, mentre coll'ajuto di di tali segni in un istante tutto salta agli occhi. [...] Quanto sin qui si è detco può essere suffìciente a far capire a Vostra Altezza che tutte le proposizioni possono essere rappresentate con figure: ma il massimo vantaggio si manifesta ne' raziocini, i quali qualora si esprimon con parole chiamansi sillogismi, in cui si tratta di tirare una conclusione esatta da alcune date proposizionì. Con tale invenzione noi potremo subito scandagliare le giuste forme di tutti i sillogismi.
Cominciamo da una proposizione affermativa universale ogni A e B. [...] Se la nozione C è contenuta interamente nella nozione A, sarà contenuta anche interamente nello spazio B (Tav. 1. fig. 8.), donde risulta questa forma di sillogismo: Ogni A è B, ma Ogni C è A, dunque Ogni C è B e quest'ultima è la conclusione ".

Torniamo ora agli aspetti didattici e domandiamoci: qual è la lezione euleriana per i matematici (gli insegnanti. gli studenti) dei giorni nostri? I diagrammi di Eulero (la cui storia può essere fatta risalire ad alcune rappresentazioni leibniziane [11]; i diagrammi di Leibniz restarono però pressocbé sconosciuti fino al 1903), infalli, sono ricchissimi di spunti. Notiamo innanzitutto che un approccio matematico avanzato potrebbe prevedere situazioni in cui i diagrammi di Eulero sono "inadatti" a rappresentare una situazione ìnsiernistica [12]: se pensiamo ai naturali secondo von Neumann, ad esempio, Ø corrisponde a 0,1 a {Ø}, 2 a{Ø, {Ø}}, 3 a {Ø, {Ø}, {Ø, (Ø}}} ecc.; dunque in tale caso se a < b abbiamo sia a∈b che a ⊆ b (ricordiamo che un insieme a tale che ∀ x(x ∈ a →x &sube a) si definisce insieme transitivo). Ebbene, come rappresentare situazioni del genere mediante diagrammi di Eulero? Osserva Jean-Philippe Drouhard [13]:
"L'impossibilità di rappresentare gli ordinali mediante diagrammi [ ... ] deriva dal fatto che gli insiemi sono rappresentati da superfici ellissoidali (in lrancese si chiamano "Les patates") mentre gli elementi sono rappresentati da dei punti, ma la nozione stessa di ordinale esige che gli elementi siano dei sottoinsiemi! [ ..] [I diagrammi] sono addirittura grossolanamente imperfetti, e ciò anche con riferimento a situazioni ben più semplici rispetto ai bizzarri ordinali. Eppur tuttavia, essi continuano ad essere usati, proprio perché si sono ben adattati ad un certo numero di situazioni elementari".

Drouhard si riferisce quindi a situazioni "ben più semplici rispetto ai bizzarri ordinali": non è difficile ideare un esempio in tal senso che potrebbe essere proposto agli allievi delle nostre scuole secondarie [14]. Premettiamo un'osservazione: spesso, nella pratica didattica, si parla di "diagrammi di Eulero-Venn". Evidenziamo però ora alcune caratteristiche che identificano i "diagrammi di Eulero" e i "diagrammi di Venn ", dovuti a John Venn (1834-1923). In generale. nei diagrammi "di Eulero" si rappresentano solo le parti (ad esempio le intersezioni) non vuote; nei diagrammi "di Venn" si raffigurano invece sempre tutte le parti: si indicano con una x le parti certamente non vuote e con un tratteggio quelle certamente vuote (le parti su cui non si hanno dati si lasciano bianche). La realizzazione di un diagramma di Venn, in senso proprio, richiede dunque di disegnare una rappresentazione in cui tutte le possibili intersezioni siano presenti. Nella pratica. didattica, però, sono i diagrammi di Eulero a risultare più "intuitivi". Ad esempio, il fatto che un insieme sia un sottoinsieme (proprio) di un altro appare immediatamente chiaro da una rappresentazione come quella sotto a sinistra. ("di Eulero", anche se in origine le figure utilizzate erano cerchi), piuttosto che da una come quella sotto a destra ("di Venn").

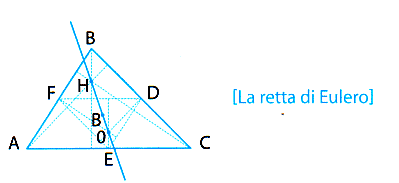
Consideriamo però la situazione seguente:
A ={1, 5}; B ={1,2}, C ={2,3}, D ={3, 4}; E ={4, 5}; F = {2: 5}; G = {3: 5}; H = {1; 4): I = {1; 3]; J = {2, 4}

e proponiamoci di rappresentarla mediante un diagramma di Eulero. Si tratterebbe di "collegare" ogni elemento di {1; 2; 3; 4; 5} in uno stesso sottoinsieme con ciascuno degli altri elementi dati, venendo così a formare i dieci sottoinsiemi indicati. Tale collegamento porta ad una "connessione" grafica dei due elementi iu gioco, in quanto un insieme è tradizionahnente rappresentato da una parte connessa di piano. Si ricordi inoltre che, per chiarezza, è opportuno che due insiemi disgiunti non siano rappresentati da parti comuni di piano (facciamo dnnque riferimento ai diagrammi di Eulero" propriamente detti: nei diagrammi "di Venn" ciò non sarebbe obbligatorio). E lasciamo ora al lettore di provare a completare l"esercizio precedente.
Dopo qualche tentativo ci si renderà conto che è impossibIle realizzare il diagramma (suggeriamo una motivazione: per ottenere la rappresentazione voluta si dovrebbe realizzare un grafo con cinque nodi completo e planare, ma è ben noto che ii grafo completo con cinque nodi K5, uno dei grafi di "Kuratowski", non è un grafo planare). Dunque la situazione descritta non può essere espressa con un diagramma di Eulero, se non a prezzo di scelte grafiche "inusuali" (come la rinuncia alla connessione della rappresentazione di un insieme; ma uno studente, a fronte di un insieme rappresentato da due "pezzi staccati" l'uno dall'altro, potrebbe pensare a due insiemi distinti!).
Domandiamoci: perché. nonostante questi "difetti", i diagrammi di Eulero sono utilizzati ampiamente nella pratira didattica? La risposta rende giustizia all'intenzione con cui il grande di Basilea introdusse la propria rappresentazione[15]. infatti, commentando le Lettere euleriane. Bruno D'Amore e Martha I. Fandiño Pinella [16] notano che per oggetto matematico va inteso tutto ciò che è indicato, segnalato, nominato quando si costruisce, si comunica o si apprede Matematica. Ora, a parte il fatto che Eulero, nel proporre i propri diagrammi, non poteva certamente riferirsi alla moderna nozione di insieme (gli articoli di Cantor saranno pubblicati nei Mathematische Annalen e in Journalfiir Mathematik a partire dal 1874), è significativo notare che la scelta di proporre una rappresentazione non va collegata ad un'impostazione platonistica mirante a dare consistenza ad un oggetto ideale; bensì può essere interpretata pragmaticamente, dunque nel senso di uno "strumento di lavoro" mediante il quale operare per realizzare procedure e dimostrazioni [17].

ROVISTANDO "NELLE LETTERE: LA "DIVISIBILITÀ ALL'INFINITO"

NELLA LETTERA CXXIII (datata 28 aprile 1761), Eulero si occopa della "divisibilità dei corpi" e fa riferimento a una "controversia fra i fllosofi moderni e i geometri". Leggiamo, sempre nella vivace traduzione di Oronzo Carnevale:

"In geometria. si può sempre dividere una linea in [due] parti eguali, per picciola essa sia. [...] Riesce anche questa stessa operazione per piccola che sia la linea AI, e per grande che si voglia il numero delle parti. [...] Da ciò ne nasce che ogni estensione è divisibile all'infinito, e questa proprietà chiamasi divisibilità all'infinito. Chi volesse negar questa proprietà che ha l'estensione, sarebbe obbligalo a sostenere che la divisione dovrebbe infine ridursi a parti così picciole, che non potrebbero più ulteriormente dividersi: perché non hanno più estensione. Intanto tutte queste particelle prese insieme debbon riprodurre quel tutto che fu. diviso; e come la quantità di ciascheduna di esse sarebbe niente o sia zero 0, molti zeri presi insieme dovrebbero produrre una quantità, cosa di cui più assurda non si può concepire".

Questa citazione può essere interpretata con riferimento ad un antico problema. Nel frammento 7 di Anassagora di Clazomene CV sec. a.c.) si legge:

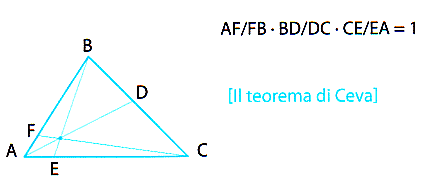
("né infatti del piccolo vi è il minimo, ma sempre un minore -ciò che è infatti non è possibile che non sia. -ma anche del grande vi è sempre un maggiore") [18]. La prosecnzione del frammento è:

("ed è eguale al piccolo in quantità, per se stessa invero ogni cosa è sia grande sia piccola").

Spesso queste parole sono state interpretate, almeno per quanto riguarda la prima parte del Frammento, con riferimento ad una successione [19]; ma proprio la seconda parte del frammento in questione non sembra essere in linea con la chiave di lettura che riporterebbe le radici del Calcolo infinitesimale al V secolo a.c. Sia Anassagora che, venndue secoli dopo, Eulero non avevano le idee del tutto chiare sulla natura degli infinitesimi. Anassagora è lontano dal 1821 , anno della pubblìcazione del Cours d 'analyse di Augustin-Louis Cauchy [un altro grande matematico ricordato nel 2007, a ceutocinquant'anni dalla scomparsa); Eulero, indubbiamente, molto meno. Ma in entrambi i casi, historia non facit saltus.

In generale, Eulero criticava le concezioni di Newton, non ritenendole in grado di spiegare la natnra dei corpi; e si oppose ai filosofi wolffiani, vicini alle idee di Leibniz sulle monadi. Sorretto dalla Fede religiosa di impronta calvinista, respingeva il tentativo di trattare congiuntamente corpo e spirito e si impegnò in prima persona nella polemica filosofica.

EULERO IN POLEMICA CON I "LIBERI PENSATORl

NELLE LETTERE EULERIANE troviamo frequenti rinessioni di carattere filosofico e religioso, grazie alle quali è possibile risalire alla visione complessiva. dell'universo da parte del loro autore: questioni, dunque, sulla natura e sulla scienza, sulla religione e, indirettamente, sulla posizione del pensatore che non si sottrae alla sfida del mondo. Eulero in effetti ebbe occasione di assumere posizioni forti nel dibattito filosofico e fu spesso bersaglio di critiche. [20]
A tale riguardo. ricordiamo che nel 1777 viene pubblicata la traduzione italiana, curata da Gregorio Fontana (1735-1803), scolopio, stimato docente di Matematica infinitesimale presso l'Università di Pavia, del Saggio di una difesa della Divina Rivelazione, in cui Eulero contestava la posizione dei "liberi pensatori" i quali negavano un principio ed una fine per l'universo. Sulla. base di alcni studi sulle orbite dei corpi celesti, Eulero sosteneva infatti che la riduzione dei periodi di rivoluzione "negli spazi celesti inondati di luce e forse di altro soltilissimo etereo fluido" (p. 56) provava che la Terra era stata, nel passato, troppo distante dal Sole perché su di essa si potesse sviluppre una forma di vita; e in un futuro l'eccessiva vicinanza del Sole l'avrebbe resa inabitabile.
Fontana, in una nota finale al volumetto euleriano (le pagine dell'appendice non sono nunerate), ricorda però alcune ricerche del "giovinetto Geometra signor De La PIace" (che, nel 1777, al momento della pubblicazione della traduzione del saggio euleriano, aveva 28 anni; ma si ricordi che già nel 1773 Laplace aveva letto davanti all'Académie Française una memoria in cui atfermava che i moti planetari sarebbero rimasti per un lunghissimo periodo vicini a quelli previsti da Newton) in contrasto con le affermazioni euleriafle: osserva inoltre che perfino i calcoli per determinare la massa delle comete di uno dei figli del grande matematico di Basilea, Karl Euler (medico di corte a Petersburg), avrebbero smentito le conclusioni del padre.
Il curatore conclude che le questioni religiose non possono essere trattate mediante le scienze esatte e scrive, nell'ultima pagina del volwnetto [21]: "Il voler appoggiare [. ..] Verità, altronde invincibilmente dimostrate e sopra irrefragabili fondamenti stabilite, ad un argomento, tratto dall'intimo seno dell'Astronomia, ciò affatto nuovo e straniero, è sempre un 'impresa di esito dubbio e incerto, perché in una materia tanto ventilata e discussa la novità. stessa dell'argomento ci mette tosto in dIffidenza della sua validità".

Questa critica di Fontana non è del tutto infondata. È inoltre spontaneo notare che effetti gravitazionali assimilabili ad un big crunch sono materia di discussione addirittura per gli astrofisici di oggi. Ogni tentativo di immaginare scenari in cui la "gravità" prenda il sopravvento e conduca a collassi apocalittici è insomma frenato dalla prudenza suggerita dalla stessa nostra sempre limitatissima conoscenza dellae forze fondamentali della natura ("gli uomini sono unicame capaci di giungere ad un picciolissimo grado di tal cognizione", come sottolinea proprio Enlero nell'opera ricordata, a p. 4) e riporta alla mente lo scambio di battute che leggiamo nella Seconda Giornata del Dialogo sopra i due massimi Sistemi del Mondo tra l'aristotelico Simplicio e Salviati, portavoce di Galileo stesso, a proposito della causa della caduta dei gravi [22]
"Simplicio: La causa di quest'effetto è notissima, e ciaschedun sa che è la gravità.

Salviati: Voi errate, signor Simplicio; voi dovevi dire che ciaschedun sa ch'ella si chiama gravità. Ma io non vi domando del nome, ma dell'essenza della cosa: della quale essenza voi non sapete punto più di quello che voi sappiate dell'essenza del movente le stelle in giro, eccettuatone nome".

Eulero non si limitava, naturalmente, alle denominazioni: ma il suo tentativo di comprendere" l'essenza della cosa" si concentrava su obiettivi ben precisi. e in fondo non sarebbe stao lontano dalla posizione di Fontana.. Per Eulero nelle parole di Gianfranco Cantelli [23), il sapere scientifico "si riferisce esclusivamente al mondo dei corpi, l'unico cui possono applicarsi i principi matematici in base ai quali ci è possibile conoscerlo"; e proprio per questo la sua indagine si preoccupò costantemente di operare "una netta distinzione tra le due nature, quella dei corpi e quella degli spiriti, primo passo decisivo per la fondazione della conoscenza scientifica della natura corporea".

Note

[1] D. Struik, Matematica: un profilo storico, Il Mulino, Bologna, 1981 (A Concise Hislory of Malhemalics, New York -Dover, 1948), p.160.

[2] G.l Bagni, "A trecento anni dalla nascita di Leonhard Euler, princeps mathematicorum" in Archimede (2007), 3, pp. "115-123·

[3] M. Gardner; Martin Gardner's Mathematical Games,
Mathematical Association of America, 2005.

[4] P. Ribenboim, The Book of Prime Number Records, Springer, New York, 1989 (terza edizione: Springer, New York, 1995), p. 136.

[5] M.L. Stein, S.M. Ulam & M.B. Wells, "A Visual Display of Some Properties of the Distribution of Primes" in American Mathematica/ Monthly (1964) 71, pp. 516-520, Si veda inoltre: http://www.maa.org/editorial/ma thgames/mathgames_07_17_06. html

[6] La dimostrazione di ciò non è elementare: Ribenboim. cit., p. 137, ricorda le ricerche sulla questione, originate da alcune osservazioni di Gauss.

[7] Si veda Ribenboim, cit., p. 142 (tali ricerche giungono peraltro ai giorni nostri con risultati di Mollin, Louboutin e Williams).

[8] Ribenboim, cit., pp. 137-142.

[9] Una dimostrazione elementare è in: G.T. Bagni, "Alla ricerca di numeri primi" in La matematica e lo sua didattica (1993) 2, pp. 166-174·

[10] L'edizione italiana in due volumi dell'opera, curata da Gianfranco Cantelli, è stata riedita nel 2007 dalla torinese Bollati Boringhieri.

[11] M.E. Baron, "A note on the historical development of logic diagrams: Leibniz, Euler, and Venn" in Malhematical Gazette (1969) 53, pp. 113-125.

[12] G.T. Bagni, linguaggio, sloria e didattica della matematica, Pitagora, Bologna. 2006. G. T. Bagni, "Some cognitive difficulties related to the representations of two major concepts of set theory" in Educationa/Studies in Mathemotics (z006) 62, 3, pp. 259-280.

[13] I.P. Drouhard, "Prefazione" a : G.T. Bagni, Rappresentare la matematica, Aracne, Roma, 2007.

[14] G.T. Bagni, Rappresentare la matematica, Aracne, Roma, 2007. Si veda anche: K.B. Chilakamarri,
P. Hamburger & R.E. Pippert, ''Venn diagrams and planar graphs" in Geometriae Dedicata (1996) 62, pp. 73-91.

[15] Si veda: M. Ferrigni, "Peirce e i diagrammi di Eulero-Venn" in Dianoia (2002) 7, pp. 205'231. E in generale: es. Peirce, Colleded Papers, I·Vlll (1931-1958), Harvard University Press, Cambridge (un'edizione italiana è: Opere, Bompiani, Milano, 2003).

[16] B.D'Amore & M.l. Fandino Pinella, " Leonhard Euler, maestro di epistemologia e linguaggio" in Bollettino dei docenti di matematica (2007) 55, in via di pubblicazione. Il riferimento è a: H. Blumer, Symbolic interactionism. Perspedive and method, Prentice Hall, Englewood Cliffs, 1969; B. D'Amore & D.J. Godino, "Punti di vista antropologico ed ontosemiotico in Didattica della Matematica" in La matematica e la sua didattica (2006) 1, pp. 9-38.

[17] Si vedano le note sul ragionamento diagrammatico peirceano in: S. Marietti, Icona e diagramma. Il segno matematico in Charles Sanders Peirce. LED, Milano, 2001.

[18] Anassagora, Frammenti e testimonianze, G. Gilardoni &
G. Giugnoli (a cura di), Bompiani, Milano, 2002, pp. 240-25.

[19] P. Dupont, Appunti di storia dell'analisi infìnitesimale. I. Le origini. Il, p. Il. Newton e Leibniz, Cortina, Torino, 1981.

[20] Si veda l'Introduzione di G. Cantelli a: L. Euler, Lettere a una principessa tedesca, I-II, Bollati Boringhieri, Torino, 2007, pp. XLXLI, in cui si osserva come "gli spiriti illuminati dell'epoca, Voltaire in testa," facessero di Eulero "bersaglio dei loro strati polemici".

[21] In L. Euler, Saggio di una difesa della Divina Rivelazione, Balzani, Pavia, 1777. Lo scritto di Fontana è nelle ultime 10 pagine; nella seconda edizione (Porcelli, Napoli, 1787) si ridurrà ad una nota e nella terza (DellePiane, Genova, 1804) sarà omesso.

[22] G. Galilei, "Dialogo sopra i due Massimi Sistemi del Mondo" in Opere, Il, UTET, Torino, 1964, pp. 291-292.

[23] In: Euler, cit., p. XVIII