Geometrie del sorriso

Sarà di certo capitato anche a voi, dopo aver superato con tenacia e pazienza il muro umano dei turisti imbambolati davanti al quadro più famoso del mondo, di farvi ammaliare dal fascino della Gioconda di Leonardo. Lo sfruttamento selvaggio dell’immagine, cui l’opera è stata sottoposta per anni, con un impiego smodato che ne ha veduto la riproduzione fin sui coperchi delle scatole dei cioccolatini, oppure l’impiego in ambito pubblicitario per reclamizzare una nota marca di acque minerali o, ancora, l’uso che gli artisti stessi ne hanno fatto, a cominciare da Duchamp che vi ha aggiunto i celebri baffetti, non ne hanno minimamente scalfito la bellezza, quando si abbia l’opportunità di vedere il capolavoro dal vero [1]. Nel momento in cui la si guarda, a dispetto del vetro di protezione che la custodisce, Monna Lisa sembra volerti parlare e pare guardare te solo in un rapporto dialogico esclusivo, capace di essere intenso anche senza parole. Un simile effetto Leonardo dovette ottenerlo non soltanto con la magia dei toni e del celebre “sfumato leonardesco” che rende l’atmosfera brumosa e soffusa, ma, prima di tutto, dosando sapientemente quegli elementi che costituiscono lo schema della composizione.

Questione di rettangoli

Il motivo di tale coinvolgimento è da imputarsi, se non esclusivamente, certo in buona parte, al fatto che l’occhio sinistro della Gioconda, ossia il destro guardando la figura, giace esattamente sulla linea mediana dell’intera composizione (fig. 1.) In altre parole: se si divide a metà il ritratto con una riga verticale, essa passerà per il centro della pupilla sinistra. Questo vuol dire che l’occhio dipinto si avvantaggia d’una simile posizione privilegiata e chi osserva monna Lisa negli occhi finisce per trovarsi, con lo sguardo, al centro del quadro.

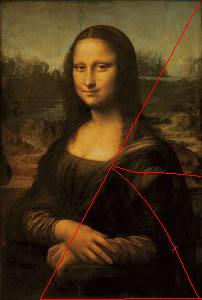
Non è tutto. Se si avrà l’accortezza di prendere in considerazione il lato lungo della tavola come se si trattasse di un segmento AB, e di ricavarvi la sezione aurea [ULB1]  secondo il semplice metodo di costruzione geometrica che individuerà il punto X, sicchè AB : AX = AX : XB, non sarà difficile constatare che quella, ossia AX, copre la distanza fra il margine superiore della tavola e il muro che si eleva alle spalle della figura (fig.2).
Se poi si avrà cura di spostare il segmento AB in modo che questo sia tangente all’angolo di quel che rimane della base di una delle due colonnine che simmetricamente dovevano inquadrare lo sfondo e la donna, si vedrà che su detto segmento è possibile costruire un rettangolo aureo che comprende l’intero dipinto, fino alla base dell’altra colonnina scomparsa [2]. Si noti che, nella costruzione del rettangolo, il passaggio tecnico che vede l’individuazione della linea mediana che segna a metà il quadrato costruito sul segmento aureo, passa esattamente per la bocca di monna Lisa contribuendo a segnare giusto il punto nel quale Leonardo dipingerà l’enigmatico sorriso (fig. 3). In ogni modo, con la realizzazione del rettangolo aureo, la figura della donna è, in pratica, tutta contenuta all’interno della nuova figura geometrica (fig. 4). La costruzione del rettangolo aureo spiega anche l’inclinazione e la collocazione delle mani di Monna Lisa. Le diagonali del rettangolo che eccede il quadrato costruito sul segmento aureo segnano, infatti, le posizioni delle mani della donna.

Ma l’immagine nasconde anche altri segreti compositivi impostati sull’impiego di opportune figure geometriche. Considerando la linea mediana della tavola, già individuata in precedenza, si possono disegnare, entro i lati lunghi del rettangolo aureo, due circonferenze d’identico raggio i cui perimetri siano, a loro volta, reciprocamente tangenti a livello della scollatura dell’abito della donna che viene così disegnata dal cerchio superiore il quale, a sua volta, ha il centro nell’occhio della figura. Ancora: dal punto d’intersezione della linea mediana della tavola con il cerchio superiore, è possibile far discendere un triangolo isoscele la cui base giace sulla linea d’angolo del muro che fa da sfondo a mona Lisa. In questo modo la parte superiore della figura è completamente contenuta dal triangolo stesso. Poi, prendendo in considerazione soltanto il cerchio superiore, non sarà difficile constatare che, all’interno di questo, è possibile individuarne un altro, concentrico, che segna l’ingombro della testa della Gioconda definendone così l’altezza (visto che è tangente all’angolo del mento) e la curva del cranio coperta dai capelli scriminati . Tenuto conto dei punti di tangenza fra la testa della donna e il cerchio appena disegnato, sarà abbastanza facile intuire che la figura geometrica che ha guidato le scelte di Leonardo deve essere stata quella dell’ottagono. Iscritto nella circonferenza e orientato opportunamente questo sarà infatti tangente all’angolo inferiore del mento, al margine inferiore della mandibola, a parte del velo, a due punti della calotta cranica e al velo che scende lungo il collo per un totale di cinque punti su otto che denomineremo con altrettante lettere . Allora, se si avrà l’accortezza di unire l’angolo in C con quello in F con un segmento, per farlo intersecare dalla linea mediana del volto che passa per la scriminatura della fronte, il dorso del naso e il tubercolo del labbro superiore, s’individuerà un punto O, che giace al centro della fronte. Da qui, aprendo il compasso con lo stesso raggio della circonferenza in cui è iscritta la testa della figura, si potrà tracciare il cerchio che sottende all’andamento enigmatico del sorriso di monna Lisa. Si otterranno così due cerchi uguali, con i rispettivi centri sul medesimo asse, ma eccentrici fra loro di poco meno della metà del raggio). 

Coincidenze evidenti

Come spesso accade, i dubbi che emergono dopo una simile lettura dell’opera d’arte cadono sull’intenzionalità o meno delle coincidenze rilevate. In altri termini, potrebbe essere il critico ad aver visto quello che, in realtà, non c’è e quella che potremmo chiamare evidenza geometrica potrebbe essere né più né meno che frutto del caso. Uno strumento utile per tentare di rimuovere queste riserve, risiede nell’analisi della personalità dell’artista preso in esame. E’ del tutto evidente, infatti, che se il pittore avesse una formazione culturale e degli interessi lontano da questo tipo di problematica apparirebbe difficile convincersi che quel che si è visto sotto la “pelle” del quadro sia stato veramente voluto.

Non è questo il caso di Leonardo. Basterebbe l’insistenza con cui Luca Pacioli ricorda, nell’introduzione al suo De divina proporzione, che sia stato proprio il genio vinciano a disegnare tutte le figure di solidi geometrici che illustravano il manoscritto originale del suo libro, per fugare i dubbi [3].

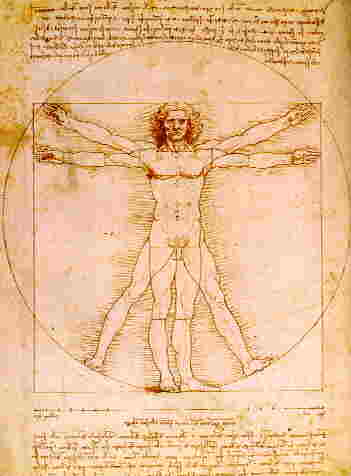
E’ quello un libro nel quale il frate di Borgo Sansepolcro aveva riversato tutto quel sapere geometrico che, partendo da Euclide “nostro philosopho”, era poi applicato alle arti figurative. Una tale collaborazione sarebbe di per sé sufficiente a dimostrare che per Leonardo la geometria descrittiva e, in particolare, l’impiego della sezione aurea, che costituisce l’argomento del testo di Pacioli, non doveva avere segreti di sorta. Non basta: un’ulteriore conferma delle scelte e degli interessi del grande artista provengono da alcuni passi del Trattato della pittura. Nei paragrafi preliminari, infatti, il Vinciano affronta una serie di problematiche come quella della comparazione fra le arti. L’idea che la pittura sia la regina delle arti e che questa sia strettamente legata alle scienze “matematiche cioè numero e misura, dette aritmetica e geometria, che trattano con somma verità della quantità discontinua e continua. Qui non si arguirà che due tre facciano più o men che sei, né che un triangolo abbia i suoi angoli minori di due angoli retti, ma con eterno silenzio resta distrutta ogni arguizione, e con pace sono fruite dai loro devoti, il che far non possono le bugiarde scienze mentali. E se tu dirai tali scienze vere e note essere di specie di meccaniche, imperocché non si possono finire se non manualmente, io dirò il medesimo di tutte le arti che passano per le mani degli scrittori, le quali non sono di specie di disegno, membro della pittura: e l’astrologia e le altre passano per manuali operazioni, ma prima sono mentali com’è la pittura, la quale è prima nella mente del suo speculatore, e non può pervenire alla sua perfezione senza la manuale operazione” [4]. In altre parole, la pittura nasce da un’operazione mentale che diviene concreta utilizzando quei principi matematici e scientifici alla base della pittura stessa (prospettiva, composizione, geometria) così da farla pervenire alla perfetta realizzazione grazie a quel processo manuale comune anche a quelle scienze che parrebbero solo mentali, come appunto la matematica e la geometria. Si tratta infatti di quella “manuale operazione” necessaria per evitare che la pittura possa confondersi con le “bugiarde scienze mentali”. Non solo, ma se con la mente voliamo alle implicazioni geometriche che sottendono la costruzione del celebre Uomo vitruviano, ritroviamo già in quel disegno il modo di procedere che ora è emerso dall’analisi della nostra opera. “Non mi legga, chi non è matematico nelli mia principi”, scriveva l’artista in margine a un foglio di studi anatomici conservato a Windsor [5]. Mi pare che ce ne sia abbastanza per ritenere intenzionale la costruzione geometrica che sottende la Gioconda.

Note

[1] Vera e propria icona della pittura, la Gioconda è stata sottoposta a quella che potremmo definire un’usura d’immagine” così grande da non avere il minimo paragone con tutte le altre, sia pure celebri, opere d’arte del Rinascimento italiano. Basterà ricordare che nel Paese dei balocchi del Pinocchio disneyano del 1939, l’opera giace da una parte mentre i monelli ci scarabocchiano sopra. Una carrellata delle operazioni più o meno discutibili che hanno interessato l’opera sta in: L’opera completa di Leonardo pittore, a cura di di A. Ottino Della Chiesa, Milano, 1978; p. 105. Sul valore e il significato dell’operazione di Duchamp, si veda: m. Calvesi, Duchamp “Art e Dossier”, 78, 1993, p. 38; Id., Il sesso della Gioconda, “Art e Dossier”, 31, 1989, pp. 30-35.

[2] Lo stato è buono, anche se si ipotizza una diminuzione del supporto lungo i fianchi di circa sette millimetri, che, però, non pregiudicherebbe in alcun modo il tipo di costruzione geometrica da noi rilevata che è tutta interna alle colonnine. Sullo stato dell’opera: F. Hours, La Joconde, Parigi 1952.

[3] “Di aritmetica si occupò appena; assai più lo interessò la geometria, dai fondamenti euclidei a speculazioni sul tipo “ludi matematici”. Già a Milano fra il 1494 e 1498 raccolse in due taccuini le proposizioni geometriche principali che costituivano – per l’arte di quel secolo – il fondamento della prospettiva e quindi il “fondamento scientifico” della pittura. Suo consigliere fu prima d’ogni altro Luca Pacioli per la cui opera […] Leonardo disegnò le figure geometriche e le rappresentazioni in prospettiva dei corpi regolari”. Da  L.H.Heydenreich, s.v. Leonardo da Vinci, in Enciclopedia Universale dell’Arte, VIII, Venezia-Roma 1958, col. 579. Si veda pure : Ch. Bouleau, La geometria segreta dei pittori, Milano 1996, pp. 85, 86 e 117. Sul numero aureo, sulla costruzione del segmento aureo e del rettangolo che ne deriva: M. Ghyka, Le nombre d’or. Rytes et rythmes pytagoriciens, I, Parigi 1931, pp. 43-56. Il testo porta riprodotti anche i poligoni leonardeschi delle tavole VII-IX e la costruzione geometrica che sottende il celebre cartone con il Ritratto d’Isabella d’Este, pure conservato al Louvre. Sulla figura di Pacioli e sul suo ritratto a opera di Iacopo de’ Barbari: M.G. Ciardi Dupré dal Poggetto, Il ritratto di Luca Pacioli e di Guidobaldo da Montefeltro, in P. Dal Poggetto (a cura di), Piero e Urbino, Piero e le Corti rinascimentali, catalogo della mostra, Urbino, Palazzo ducale 24 luglio-31 ottobre 1992, Venezia 1992, pp. 197-204.

[4] Leonardo da Vinci, Trattato della pittura, a cura di A. Zevi, Milano 1982, pp. 27-28.

[5] L.H.Heydenreich, op. cit., col. 578. Sugli aspetti geometrici e antropometrici dell’Uomo vitruviano di Leonardo: M. Bussagli, A misura d’uomo, “Art e Dossier”, 146, 1999, pp. 17-20.

[ULB1] Considerata per secoli la misura per eccellenza, così da essere applicata in pittura come in architettura, la sezione aurea è quella parte di un segmento AB e la sua parte restante, secondo l’equazione già ricordata: AB:AX = AX:XB. Si prenda allora un segmento AB e lo si divida a metà e si riporti in verticale individuando un punto O. Si unisca O con A. Si punti il compasso in O con apertura OB e si individui su OA un punto H. Si punti il compasso in A con apertura AH e  si riporti su AB individuando un punto X. AX è la sezione aurea su cui è possibile costruire un rettangolo aureo. Si costruisca un quadrato di lato AX (AXBC) e lo si divida a metà con un segmento DE. Si unisca C con E. Si punti il compasso in E con apertura CE. S’individui un punto F sul prolungamento di AX. AF sarà il lato lungo del rettangolo aureo AFGC.