I pavimenti di Carlo Scarpa

I pavimenti di Carlo Scarpa

 

A quasi mille anni dalle opere dei Cosmati, l’evoluzione più interessante è costituita da un affinamento della capacità di valutare cosa sia riconoscibile come pattern, l’acquisizione di un più sofisticato “senso dell’ordine”. Il pavimento che l’architetto italiano Carlo Scarpa progettò, nel 1961, per uno spazio relativamente piccolo all’interno del museo del palazzo Querini Stampalia a Venezia, è un segno di questo mutamento (Figura 8) [11].

Figura 8

L'ingresso del Palazzo Querini-Stampalia a Venezia con il pavimento Colorato di Carlo Scarpa (foto Judith Moran)

È difficile immaginare un progetto di pavimentazione più lontano da quello dei Cosmati, che probabilmente sarebbero rimasti alquanto perplessi di fronte a questo pavimento contemporaneo. Anche un occhio moderno è disorientato da una disposizione apparentemente casuale e non coglie cosa l’architetto intendesse come motivo. Sicuramente non vi è un evidente organizzazione dello spazio, non vi sono direzioni implicate paragonabili al passaggio centrale così caratteristico dei pavimenti dei Cosmati.

Per apprezzare pienamente il lavoro di Scarpa, bisogna veramente visitare Venezia. L’acqua è l’elemento dominante nell’area in cui il pavimento è collocato (attualmente quando la marea sale,l’acqua penetra addirittura negli spazi interni). Il disegno del pavimento riflette ed estende il motivo e i colori della grata in rame, che separa l’anticamera della stanza dal canale. Ma, oltre alla sua superba funzionalità in questo spazio, il pavimento esibisce una sottile strategia completamente specificata da Scarpa. L’architetto ha creato il pavimento utilizzando un modulo che impiegò in almeno altri tre suoi progetti: il palazzo Querini Stampalia, la Chiesa del Torresino a Padova (1978) e il Museo di Castelvecchio di Verona (1956). Il modulo è un quadrato, di cui un quadrante è costituito da un area di colore e/o texture contrastante. Visivamente, si può percepire come una forma a L riempita con un quadratino. Nel palazzo Querini Stampalia, Scarpa ha utilizzato due marmi chiari (crema e rosa-beige) per la forma a L e due più scuri per il quadratino (rosso e verde) combinati in quattro diversi moduli colorati. Le quattro rotazioni di ognuno di questi moduli danno 16 diverse unità orientate. Il motivo complessivo del pavimento è il risultato della combinazione di queste 16 unità (Figura 9).

Figura 9

Rilievo del palazzo Querini-Stampalia progettato da Carlo Scarpa (rilievo Kim Williams)

A prima vista, può sembrare che le unità nel pavimento di Scarpa siano disposte a caso. I suoi schizzi per il disegno del pavimento ci mostrano, invece, quanta cura abbia posto nel disporre e codificare, secondo i colori, le singole unità affinché niente nella realizzazione fosse lasciato al caso. I disegni ci indicano con chiarezza quanto Scarpa abbia meditato su come disporre le unità per ottenere un effetto complessivo di marezzatura (a richiamare il motivo dell’acqua nel canale a fianco). Ma, anche se non disponessimo dei disegni cui riferirci, avremmo comunque la prova che i moduli non sono messi a caso osservando quali combinazioni non compaiono mai. La prima configurazione della Figura 10, ad esempio, compare una sola volta, mentre la seconda ricorre solo cinque volte. Scarpa utilizza i colori per scompaginare questi due raggruppamenti fortemente simmetrici. Infatti la configurazione della Figura 10 non compare mai con i tre elementi che formano la L della stesso colore (invitiamo il lettore a cercare altri esempi).

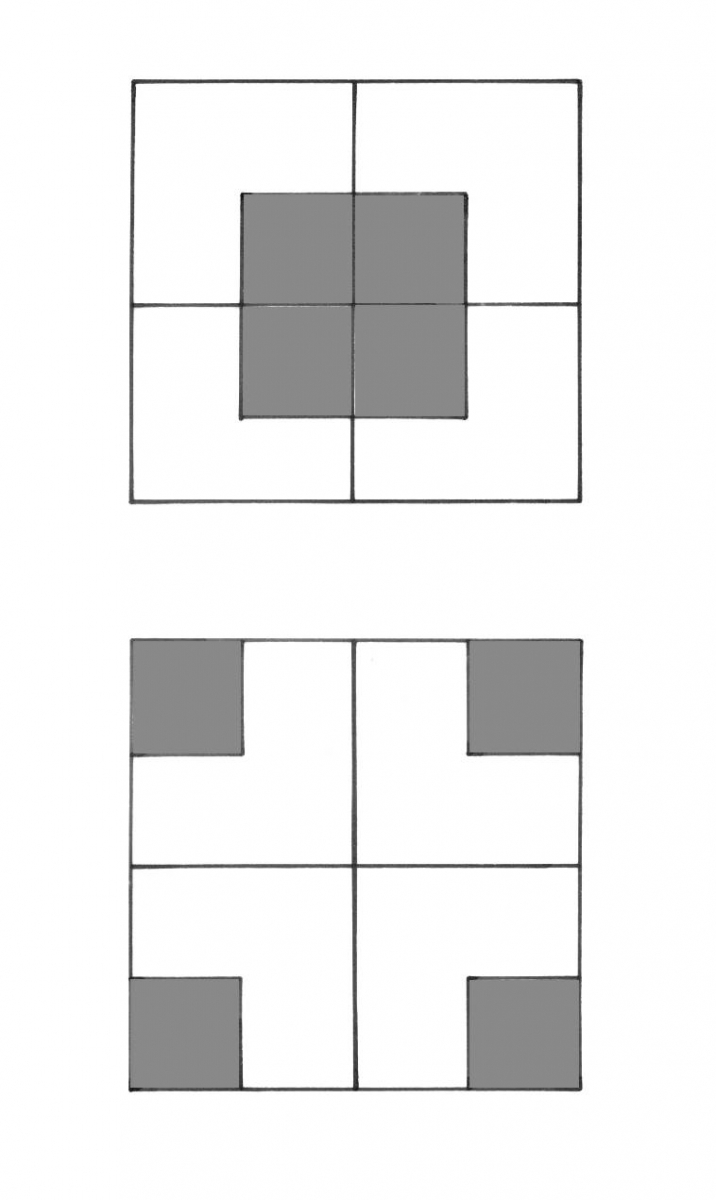
Figura 10

Le due disposizioni delle singole unità compositive di Carlo Scarpa, con il più alto grado di simmetria

Se distinguessimo le configurazioni di quattro moduli in un quadrato solo dalla posizione del quadratino scuro, non considerando i colori, avremmo esattamente sedici possibilità. Ipotizzando una disposizione dei moduli casuale, ognuna di queste sedici combinazioni dovrebbe comparire lo stesso numero di volte attorno ad ognuno dei 600 vertici del pavimento (dove si incontrano sempre quattro quadrati). In base a queste considerazioni, dovremmo avere dozzine di copie delle configurazioni altamente simmetriche della Figura 10.
Il fatto che la prima configurazione ricorra in una sola copia, mentre la seconda compaia solo in tre occasioni, e queste ultime siano ulteriormente differenziate dall’uso di due diversi colori dei moduli, indica come l’autore le abbia volutamente escluse. Si direbbe che Scarpa abbia voluto evitare ogni disposizione del motivo che potesse attrarre o fissare lo sguardo dello spettatore in una data zona. Ne Il senso dell’ordine Gombrich dichiara “i nostri occhi sono attratti dalle zone dal più alto contenuto di informazione” come i centri di simmetria rotatoria in un disegno o gli assi di simmetria speculare di un motivo. [12]. Sembra che Scarpa abbia voluto sottrarre questi “contenuti di massima informazione” agli occhi degli spettatori.

Benché i pavimenti di Scarpa e dei Cosmati abbiano molte più differenze che somiglianze, vi è un tipo di simmetria che li accomuna: quella di auto-somiglianza, che appare in forma più compiuta nei Cosmati e in modo più embrionale in Scarpa. La porzione a L del modulo di Scarpa assomiglia alla sedia o L-modulo, uno dei rep-tiles di Solomon Golomb. [13] Un rep-tile è un poligono che può essere decomposto in submoduli congruenti, ognuno simile all’originale. La Figura 11 ci mostra come entrambi gli L-moduli e il triangolo equilatero siano dei rep-tiles.

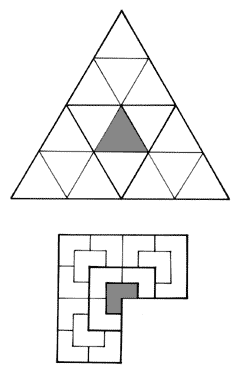
Figura 11
(a, sotto) "La sedia" o L-modulo, un rep-tiles di Solomon Golomb; (b, sopra) il "rep-tile" composto da triangoli equilateri. Entrambi gli esempi sono riportati al terzo livello (il primo livello è composto da una singola unità; il secondo livello è composto da quattro unità; il terzo livello è composto da 16 unità). L'insieme mantiene sempre la forma dell'unità originaria.

Un rep-tile può essere utilizzato per generare una pavimentazione del piano attraverso un processo che prevede dapprima la decomposizione di un modulo nei suoi sub-moduli congruenti e quindi la dilatazione della configurazione risultante fino a che i sub-moduli abbiano raggiunto le dimensioni dell’originale. Il procedimentosatura il piano attraverso decomposizioni e dilatazioni iterate ad infinitum (un procedimento di questo tipo, naturalmente, è condotto più efficacemente da un computer piuttosto che da un artigiano del dodicesimo secolo!).

Possiamo osservare i primi stadi di questo procedimento nel setaccio di Sierpinski prodotto dai Cosmati e, in modo più imperfetto e limitato ad alcune aree, nel pavimento di Scarpa. Naturalmente Scarpa non utilizzò questo metodo di decomposizione e inflazione per disegnare il suo pavimento per il palazzo Querini Stampalia. Ma, in seguito all’uso di diversi colori nel suo modulo base quadrato, possiamo notare numerose ricorrenze nel pavimento di regioni quadrate composte di quattro dei suoi moduli che contengono una elle composta di quadrati color crema, con l’inserto di un quadrato beige. Troviamo anche aree quadrate consistenti di sedici moduli, dodici color crema (formanti le L) e un’area più scura formata da quattro quadrati beige. Questi quadrati più scuri sono composti a loro volta da una L fatta da tre moduli beige e uno crema. Dato che le L di secondo e terzo stadio sono decomposte in quadrati e non da moduli a L, anche queste aree del pavimento non possono essere considerate esempi compiuti di rep-tiling.

Il pavimento di Scarpa si distingue da quelli dei Cosmati, oltre che per le notevoli differenze nell’uso delle simmetrie (molto presenti nei pavimenti dei Cosmati, molto sfumate nel disegno di Scarpa) anche per l’utilizzo che fa del colore. Nei pavimenti cosmateschi, l’uso dei contrasti di chiarezza è molto importante, mentre il colore, di per sé, appare applicato in modo quasi casuale.Nei pavimenti di Scarpa, invece, il colore è coscientemente utilizzato per creare il repertorio base di sedici unità individuabili e differentemente orientate.

Il pavimento di Scarpa – come detto – è stato progettato con grande cura e pertanto non può certo essere definito come insieme disordinato, ma riflette sicuramente un tipo di ordine diverso rispetto a quello che troviamo in un motivo dei Cosmati. Probabilmente, l’aspetto più interessante è che ora il possibile ordinamento viene meno non appena l’occhio sembra aver individuato una regola sottostante.

Ma, se il disegno del pavimento di Carlo Scarpa per il palazzo Querini Stampalia, rifiuta descrizioni nei termini delle simmetrie convenzionali e se lo si può definire quasi ordinato (nel senso che alcune proprietà sono rintracciabili solo in alcune parti e non sempre in modo regolare) è corretto classificarlo come pattern? Forse la risposta sta in ciò che Gombrich chiama “il fatto più fondamentale nell’esperienza estetica”: “il piacere spesso sta da qualche parte tra la monotonia e la confusione”. [14]