Il Calcolo delle probabilità e la Teoria dei Giochi
"La teoria della probabilità non è in fondo che buon senso ridotto a calcolo; essa permette di valutare con esattezza ciò che le menti illuminate sentono per una specie di istinto senza rendersene conto... E' notevole come tale scienza, che è cominciata con gli studi dei giochi d'azzardo, si sia elevata ai più importanti oggetti delle conoscenze umane".
Così si esprimeva, circa due secoli fa, Blaise Pascal (Clermont-Ferrand, Puy-de-Dôme, 19 giugno 1623 – Parigi, 19 agosto 1662) matematico, fisico, filosofo e religioso francese a proposito dell' argomento che ci impegnerà in questo articolo: la probabilità, appunto.
1. La storia
“Tutto ciò che non è lavoro è gioco”, recita un vecchio detto popolare, e noi partiamo proprio dalla storia del gioco per arrivare ad importanti concetti matematici e alla loro applicazione in ambiti molto diversi tra loro.
Il gioco d'azzardo, nel quale si scommettono somme più o meno grandi, era già noto agli antichi Romani, anche se non era approvato ed era ammesso solo durante il periodo dei Saturnali (antica festività in onore del dio Saturno), che si celebravano ogni anno, in origine, per un solo giorno (pare il 17 dicembre), poi, in età imperiale, per più giorni (forse quattro o cinque). Per il resto dell'anno il gioco era proibito e chi trasgrediva la legge veniva punito con un'ammenda che ammontava fino a quattro volte la posta in gioco.
“Dura lex, sed lex”, dicevano proprio i Romani, ma, forse, solo per i comuni mortali, perché la leggenda vuole che l'imperatore Augusto non osservasse scrupolosamente questa disposizione, anche se, ovviamente, nessuno osava farglielo notare.
Che l'imperatore amasse il gioco è testimoniato da una sua lettera in cui afferma : “Abbiamo passato piacevolmente le festività [...] Abbiamo giocato tutti i giorni e il foro dei dadi si è proprio infiammato”.
Uno dei giochi praticati era il cosiddetto "Capita aut navia", quello che noi chiamiamo “testa e croce”: anche in quel caso si lanciava in aria una moneta, sulle cui facce si trovavano rispettivamente la testa di Giano bifronte (Capita) e una nave (navia)
Diffuso anche il gioco degli astragali, di origine antichissima, tanto che vengono persino nominati nell'Iliade di Omero; essi consistevano in ossa brevi, tratte dalle articolazioni delle zampe posteriori di capre o montoni, ed erano utilizzati dagli antichi come dadi per la loro particolare forma, che ricorda un po' quella cubica.
Al British Musuem di Londra è custodito un gruppo realizzato in terracotta che raffigura due fanciulle impegnate nel gioco degli astràgali, datato 330-340 a .C.
Gli astragali (se ne utilizzavano quattro) avevano quattro facce utili, su ciascuna delle quali era dipinta una figura cui veniva attribuito un punteggio diverso: per esempio, il peggiore lancio si verificava quando compariva la faccia su cui si trovava l'immagine di Anubis, il dio sciacallo delle necropoli egizie, che dai Greci veniva definito kion ossia cane (anche per i Romani), il cui punteggio era solamente 1; la faccia opposta, che era dedicata a Venere, valeva 6 punti, il massimo.
Già ai tempi dei Romani quello dei dadi sicuramente era il gioco più diffuso: è tristemente famoso l'episodio del Vangelo secondo cui i soldati lo utilizzarono per dividersi tra di loro i vestiti di Gesù.
Il gioco dei dadi sostituì man mano quello degli astragali il cui uso si perse nel tempo, anche se non conosciamo il periodo esatto.
Una curiosità: secondo la tradizione greca antica fu Palamede, re di Eubea, ad inventare i dadi da gioco durante la guerra di Troia. L'immagine a fianco rappresenta Achille e Aiace giocano ai dadi, (particolare di un vaso greco del VI a.C. conservato presso i Musei Vaticani).
Nel corso dei secoli, comunque, sia la Chiesa che lo Stato vietarono con leggi e bandi la pratica del gioco, non tanto per il gioco di sorte in sé, quanto per i vizi “indotti” che lo accompagnavano: la bestemmia e il bere combattuti soprattutto dalla Chiesa, mentre lo Stato si preoccupava dello sperpero dei beni posseduti dai giocatori e dei crimini in cui spesso erano coinvolti.
Ciononostante, il gioco d'azzardo (dall'arabo al zhar ,dado, più precisamente zhar è il fiore d'arancio dipinto sul dado) fu per molti secoli il passatempo preferito, anche perché non esistevano tanti modi di divertirsi: molti frequentavano i teatri, ma sicuramente il gioco d'azzardo attirava tutti, dal nobile all'uomo del popolo. E i giochi andavano dai già nominati dadi, alla morra, alle carte, alla “zara”, menzionato persino da Dante nel VI Canto del Purgatorio quale similitudine tra se stesso e i partecipanti a tale gioco.
Giocare e scommettere, dunque. A questo proposito vorrei ricordare la nascita del moderno “lotto”, che avvenne a Genova nel 1576: l'idea era stata di Andrea Gentile ed era legata all'elezione di cinque senatori fra centoventi cittadini del Consiglio, utilizzando un'estrazione a sorte con tanto di bussolotti, corrispondenti ciascuno a un senatore.
Questo tipo di lotto, chiamato "Gioco del Seminario" (dal nome dell'urna in cui avveniva l'estrazione), si svolgeva tramite scommesse che la popolazione piazzava sui propri favoriti.
2. Lo studio della probabilità
Ed proprio dal gioco d'azzardo che ebbe inizio lo studio sistematico del Calcolo delle probabilità che nasce nel Seicento per risolvere alcuni problemi sui dadi posti da un giocatore, il cavaliere de Méré, a B. Pascal, del quale rimane, sull'argomento, un carteggio di sei lettere (tre per parte), datato 1654, con il matematico P. Fermat, su cui ci soffermeremo più avanti.
In effetti già Luca Pacioli nel suo “ Summa de aritmetica, Geometria, proporzioni et proporzionalità” datato 1494, aveva trattato l'argomento insieme al cosiddetto problema delle parti che consiste nel calcolo di come deve essere divisa la posta di una certa partita se essa viene interrotta prima che vi sia un vincitore.
I primi studi conosciuti su questioni di probabilità si riferiscono al gioco dei dadi e compaiono nel libro De ludo aleae (Il gioco dei dadi) di Girolamo Cardano (1501-1576), a sua volta appassionato giocatore.
Vale la pena soffermarsi un momento sulla vita di questo studioso piuttosto originale ed eclettico, che non si occupò solo di Matematica dove, peraltro, raggiunse discreti, anche se discussi risultati, ma di Medicina, di Fisica, di Astrologia, di Meccanica (ricordate il giunto cardanico?), di Alchimia e di Scienze.
Figlio illegittimo di un avvocato e di una vedova molto più giovane, Gerolamo venne avviato allo studio della Matematica proprio dal padre, appassionato di tale disciplina, che insegnava Geometria all'Università di Pavia e pare fu consultato anche da Leonardo.
Iniziò i suoi studi di Medicina proprio a Pavia, ma li terminò a Padova. Come medico ebbe molto successo: la sua fama si estese anche in Europa, tanto che nel febbraio 1552 fu invitato a curare John H. Hamilton, arcivescovo cattolico di St. Andrews a Edimburgo, sofferente, si credeva, di tisi, che, col tempo, era andata aggravandosi.
Come ci racconta Attilio Zanca nel suo libro “Cardano medico e taumaturgo”, Cardano partì il 22 febbraio 1552 e il 13 marzo giunse a Lione dove avrebbe dovuto incontrare l'arcivescovo scozzese; dopo un breve soggiorno, ritornarono in Scozia e il nostro medico diagnosticò che la malattia dell'arcivescovo era asma, causata dalla vita disordinata condotta dal prelato. Gli ordinò una dieta, diremmo oggi, più equilibrata, e di sostituire i cuscini e i materassi di piuma del letto dove dormiva con altri di seta grezza perché “seggendo sulle quali in fama non si vien": l'intuizione fu vincente perché l'arcivescovo guarì rapidamente e, naturalmente, lo ricompensò con molta generosità.
Oggi possiamo pensare che la malattia di Hamilton fosse di origine allergica e che l'asma fosse causata dagli acari delle piume: se pensiamo che queste conclusioni furono dimostrate nel 1964 possiamo capire la grandezza di Cardano. Se come medico ebbe notevole successo, non altrettanto si può dire della sua esperienza di astrologo: fece l'oroscopo di Gesù Cristo, ma la Chiesa che già non apprezzava l'Astrologia in generale, a maggior ragione lo accusò di eresia e lo mise in prigione per tre mesi, più altrettanti di quelli che oggi chiameremmo “arresti domiciliari”. Maggior fortuna non ebbe con le profezie pronunciate, rispettivamente, per l'arcivescovo - cui annunciò successo e felicità perenni - e per il giovane Edoardo VI, per il quale previde una vita oltre i cinquantacinque anni: il primo fu impiccato a Stirling nel 1571, senza processo, dai riformatori scozzesi, mentre Edoardo VI morì di tubercolosi nel giro di un anno.
Ma torniamo al Cardano matematico: egli fu il più famoso algebrista del Cinquecento. Si rese protagonista di un episodio che non lo mette certamente in buona luce. Il fatto è legato ad un altro matematico, Nicolò Fontana da Brescia detto il Tartaglia (per la balbuzie dovuta alle ferite alla testa inferte da un soldato francese durante il sacco di Brescia nel 1511). La questione riguardava la risoluzione delle equazioni di terzo grado e, dai documenti pervenutici, sembra che il nostro Cardano non si sia comportato in maniera molto corretta nei confronti di Tartaglia.
Come abbiamo già detto, Cardano scrisse De Ludo Aleae sul gioco dei dadi (scritto intorno al 1525 ma pubblicato postumo nel 1663); egli amava molto questo tipo di gioco, nel quale, da una parte dissipò molte delle sue sostanze, dall'altra qualche volta costituì un modo per incrementare le sue entrate, vincendo più di quanto perdesse, anche se era solito affermare che “..l'unico vantaggio deriva dal non giocare per niente....".
Nella speranza di aumentare le sue possibilità di vittoria, egli studiò a fondo il gioco a tal punto che può essere considerato il primo ad aver gettato le basi della moderna Teoria della probabilità; infatti nell'opera egli definì la probabilità come rapporto tra il numero dei casi favorevoli e quelli possibili ed enunciò due importanti teoremi: la probabilità dell'evento prodotto logico (A e B) di due eventi semplici A, B e una anticipazione della legge dei grandi numeri.
Anche Galileo Galilei, qualche anno più tardi, intorno al 1630, si occupò di probabilità ed il suo contributo fu notevole: nell'opera “Sulla scoperta dei dadi”, come Pascal fa il calcolo dei casi favorevoli all'avverarsi di evento rispetto a tutti quelli possibili. Su richiesta di un gruppo di nobili fiorentini che volevano capire come mai nel gioco a tre dadi detto “Zara” uscissero di più (abbiano una frequenza maggiore, diremmo oggi) il 10 e l'11 rispetto al 9 o al 12, Galileo calcolò che esistono 27 modi per ottenere il 10 e l'11 da tre dadi contro i soli 25 per il 9 e il 12.
Ormai è chiaro che lo studio sistematico della probabilità è nato dall'esigenza di risolvere dei problemi puramente pratici legati al gioco d'azzardo; e fu proprio per questo motivo che Blaise Pascal nel 1654 cominciò ad interessarsi a questo ramo della Matematica. Infatti, come abbiamo già accennato, un cavaliere (un certo De Mère) gli pose una serie di quesiti sul gioco dei dadi, alcuni dei quali piuttosto contorti. Uno di questi è il seguente:
esiste la stessa probabilità di vincere scommettendo che esca almeno un 6 su 4 tiri consecutivi, lanciando un dado alla volta, oppure scommettendo che escano almeno due 6 su 24 tiri, lanciando due dadi alla volta?
Pascal discusse di questo e degli altri problemi con Fermat in un carteggio formato da sei lettere. Secondo il Cavaliere De Meré, la risposta avrebbe dovuto essere positiva. Ecco il suo ragionamento:
Si può assumere che su 6 lanci ogni faccia esca una sola volta, cioè le possibilità di avere un 6 sono 1 su 6. Effettuando 4 lanci, queste possibilità dovrebbero essere 4*1/6 = 2/3 .
Se si lanciano due dadi, sui 36 risultati possibili solo uno sarà un doppio sei, quindi la possibilità di fare un doppio 6 ad ogni lancio si può porre uguale a 1/36. Su 24 lanci, la possibilità diventa 24*1/36 = 24/36 = 2/3.
Purtroppo si accorse del proprio errore a spese del suo patrimonio e questo lo indusse a chiedere aiuto a chi era più esperto.
Pascal, insieme a Fermat, fornì la risposta giusta calcolando quanti sono i casi favorevoli allo scommettitore rispetto a tutti i casi che si possono verificare, giungendo alla conclusione che il doppio 6 su 24 lanci è un evento più difficile a realizzarsi di un singolo 6 su 4 lanci.
Per il lettore amante di questo tipo di esercizio forniamo la soluzione, utilizzando la notazione moderna:
La probabilità dell'evento “in 4 lanci di un dado esce almeno una volta 1”
equivale alla probabilità contraria dell'evento
“in quattro lanci non esce nemmeno una volta 1”.
In altri termini, se indichiamo rispettivamente con p e q le probabilità dei due eventi, risulta p = 1 - q . La probabilità q è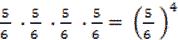 
.
Quindi p = 1 -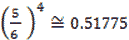 
La probabilità dell'evento
“in 24 lanci di due dadi esce almeno un doppio 1”
equivale alla probabilità contraria dell'evento
“in 24 di due lanci di due dadi non esce nemmeno una volta un doppio 1”.
In altri termini, se indichiamo rispettivamente con p e q le probabilità dei due eventi risulta p = 1 - q.
La probabilità q è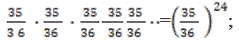 
da cui ricaviamo
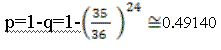
Non ci soffermiamo sulla figura di questo studioso, ma ricordiamo che egli è considerato tra i fondatori della Meccanica e dell'Ottica fisica e che il suo nome è legato a importanti scoperte astronomiche e nel campo della Fisica.
Intorno al XVII secolo lo studio della probabilità si staccò dai problemi di gioco per entrare in qualcosa di più “serio” e, grazie ad un commerciante di stoffe inglese, John Graunt, fu applicato alle Scienze sociali.
Graunt, insieme a Malthus, può essere considerato il fondatore della Demografia, cioè quella scienza che studia, da un punto di vista quantitativo, tutto ciò che riguarda i movimenti delle popolazioni.
Egli cominciò a consultare i cosiddetti Bills of mortality (Bollettini di mortalità) che fornivano la lista dei morti e delle nascite in alcuni quartieri di Londra, in cui erano indicate anche le cause di morte: questi bollettini erano spesso consultati dai ricchi londinesi per conoscere l'insorgere di eventuali epidemie di peste e, quindi, mettersi al sicuro lontano dalla città.
Per Graunt , invece, questi dati diventarono la base di un approfondito studio per compiere diverse analisi; per esempio, stimare la popolazione della capitale: egli scoprì che nel 1660 c'erano state circa 3 morti ogni 88 persone, per cui essendoci stati 19200 decessi, 19200 * = 563200 è la stima calcolata.
Inoltre egli studiò le cause biologiche, sociali ed economiche della mortalità, lo studio del rapporto tra i sessi, la differenza tra nascite e morti in città e campagna, i flussi migratori.
3. Bernoulli e la Legge dei grandi numeri
Nel nostro excursus storico sulla probabilità arriviamo al 1713, dove incontriamo Jakob Bernoulli, matematico e scienziato svizzero, e la sua opera Ars conjectandi; in essa troviamo i concetti anticipatori del calcolo delle probabilità, insieme ai cosiddetti numeri di Bernouilli e al primo enunciato della legge dei grandi numeri, oggi fondamentale per le Scienze statistiche.
Non ci soffermiamo sui numeri di Bernoulli (che richiedono l'introduzione di formule non molto semplici per i non addetti ai lavori); invece vorrei approfondire il significato della “legge dei grandi numeri” o teorema di Bernoulli e le sue applicazioni.
“In base a esso, se E è un evento e p è la probabilità (costante) di successo, cioè la probabilità del verificarsi di E in una prova, allora la frequenza relativa dei successi su n prove indipendenti eseguite converge a p', cioè se il numero n delle prove effettuate è sufficientemente grande, è quasi certo che la frequenza relativa dei successi nelle n prove differirà assai poco dalla probabilità di successo nella singola prova”.
Vediamo di capire meglio con un esempio: se lanciamo una moneta, tutti sappiamo che la probabilità che esca “testa” è del 50%, cioè ½, e così per la probabilità che esca “croce”. Ciò significa che se eseguo dieci lanci otterrò esattamente 5 volte “testa” e cinque volte “croce”? Certo che no, rispondiamo tutti: per quanto ne so a priori, potrei ottenere dieci uscite dell'una e zero dell'altra. Se però effettuo un numero molto grande di tentativi, la frequenza (cioè il verificarsi di uno dei due eventi), per esempio l'uscita “testa”, si avvicina, cioè tende alla probabilità teorica, nel nostro caso ½. Se vogliamo ancora un esempio per chiarire ulteriormente, pensiamo al sesso di un nascituro: anche in questo caso la probabilità che sia maschio o femmina è del 50%, ma su quattro figli non è detto che due siano maschi e due femmine. Se però pensiamo, ai nati in Italia, per esempio nel 2005, quindi un numero abbastanza grande, scopriamo che i nati sono in tutto 554022 di cui 268325 femmine e 285697 maschi. E' facile (con la calcolatrice…) calcolare il rapporto tra nati femmine o maschi e quella totale (circa 0,51 nel primo caso e 0,48 nel secondo) e si vede che tale rapporto tende a 0,5.
La parola “tende” è stata sottolineata per due motivi: il primo è che questa semplice parola in Matematica rappresenta un importante concetto, quello di limite ; il secondo perché ci servirà, più avanti, a confutare alcune false credenze propinate ai giocatori del lotto per convincerli a continuare a puntare, mascherando le motivazioni sotto una falsa parvenza scientifica.
Abbiamo già visto che la probabilità si calcola come rapporto tra i casi ritenuti favorevoli al verificarsi di un evento e quelli ritenuti possibili; ora introduciamo il concetto di speranza matematica che ci porterà a quello di gioco equo .
Si definisce “speranza Matematica”il prodotto della somma da vincere per la probabilità di vincerla; per esempio se la probabilità p=1/18 è la probabilità al gioco del Lotto che esca un numero su una determinata ruota (spiegheremo più avanti come si perviene a questo valore) ed io gioco 1 €, la speranza matematica è
1 € x €, cioè circa 0,056 €
Come si nota, la speranza matematica è un valore espresso, per esempio, in Euro.
Se vogliamo capire meglio il significato di questo concetto, possiamo dire che esso rappresenta la previsione della vincita media per partita che si avrà facendone un numero molto elevato.
Questa nuova nozione ci porta ad un'altra, il cosiddetto gioco equo : esso si verifica quando il prezzo del gioco è uguale alla speranza Matematica della vincita, cioè se alla fine i giocatori si trovano a non aver guadagnato nulla, ma anche a non aver perso nulla, ovvero se la speranza Matematica di ciascun giocatore è nulla. Quindi:
Prezzo pagato = Vincita * probabilità.(1)
Di qui ricaviamo che la somma che dovremmo ricevere in caso di vincita è pari al rapporto tra il prezzo pagato e la probabilità, sempre che il gioco sia equo.
4. Il gioco del lotto
Vediamo di applicare tutti i concetti finora appresi a quello che Bruno De Finetti, grande matematico italiano morto nel 1985, definiva “la tassa sull'imbecillità”: il gioco del Lotto.
Diamo inizio, allora, al nostro processo con l' obiettivo di dimostrare, al di là ogni ragionevole dubbio, che tutte le teorie su numeri ritardatari, numeri gemelli, numeri spia e chi più ne ha ne metta, sono false.
La prima cosa da stabilire è che non è un gioco equo e che l'unico che veramente “guadagna”(il giocatore può “vincere”, ma non guadagnare) è lo Stato che lo gestisce. Infatti, se il gioco fosse equo, chi indovina un numero su una determinata ruota dovrebbe vincere 18 volte la posta giocata, mentre invece lo Stato paga circa 11 volte la quota; se si indovina un ambo si incassa 250 volte la somma scommessa, anziché 400, e così via.
Passiamo poi ad un'altra truffa perpetrata ai danni di giocatori ingenui da sedicenti “esperti” in quella che è stata chiamata lottologia scientifica e cioè la teoria sui numeri ritardatari.
Innanzi tutto dobbiamo confutare la convinzione che l'uscita dei suddetti numeri sia legata alla legge dei grandi numeri, legge sicuramente valida, ma usata in maniera errata per mascherare con principi matematici reali ciò che, invece, è un inganno bello e buono e sedurre, così, i più sprovveduti e incitarli a continuare a puntare e a spendere denaro.
Tacito, considerato uno degli storici più importanti dell'antichità (nacque intorno al 55 d. C) e autore degli “Annales”, diceva " La speranza di diventare ricchi è la più diffusa causa di povertà": quanto è attuale questa affermazione e come si collega alle nostre argomentazioni!
I telegiornali e la stampa, in genere, esaltano con servizi particolarmente accattivanti e convincenti le vincite milionarie (rare), ma porgono poca o nessuna attenzione ai casi di persone che si sono rovinate per il gioco del lotto e per la tristemente famosa teoria dei numeri ritardatari: qualche anno fa u n impiegato di una banca dell'Oltrepò pavese è stato licenziato, perché aveva sottratto un milione di euro dai conti correnti dei clienti per giocare il 53 sulla ruota di Venezia, in ritardo da molte settimane, mentre altre quattro persone si sono suicidate , dopo aver dilapidato i beni di famiglia, continuando a puntare sul numero; ma queste sono storie che non fanno notizia.
Nel sito prima citato è riportata questa affermazione: " La tradizione vuole che l'estrazione di certi numeri "preannunci" l'uscita di altri”.
Ma questa dichiarazione ha il significato scientifico che alcuni cercano di attribuirle? Vediamo di rispondere nel modo più rigoroso e, nello stesso tempo, più chiaro possibile.
Già ai primi dell'ottocento, il già citato De Laplace scrisse: “ Quando un numero non esce da molto tempo, i giocatori corrono a coprirlo di danaro, essi ritengono che quel numero reticente debba uscire al primo colpo, a preferenza di altri, ma il passato non può avere alcuna influenza sull'avvenire”.
Qualcuno, come abbiamo già detto, si appella alla legge dei grandi numeri per avvallare la propria tesi secondo cui l'affermazione precedente è vera: chi fa ciò o ha letto in maniera molto superficiale qualche manuale di probabilità o è in mala fede.
Infatti ogni numero ha sempre la stessa probabilità di essere estratto (a meno che non ci sia frode, con bussolotti riconoscibili al tatto o altri imbrogli). Non è affatto vero che i numeri con maggiore ritardo abbiano più probabilità di uscire rispetto agli altri: i numeri sono "senza memoria", come si dice, tutti hanno la stessa probabilità d'uscita, indipendentemente da ciò che è successo in precedenti estrazioni, cioè la probabilità continua ad essere 1/18.
Non è facile convincere gli accaniti giocatori che se un numero è uscito molte volte (o poche) nelle estrazioni precedenti, allora dovrà uscire più raramente (o viceversa più spesso) nelle successive in modo che il valore della frequenza si avvicini a quello della probabilità, perché questo è ciò che afferma la Legge dei grandi numeri, secondo molti falsi “esperti”.
Questa è un'interpretazione distorta della Legge.
Intanto essa è applicabile e risulta vera per numeri dell'ordine di molte decine di migliaia, mentre il ritardo dei numeri è dell'ordine delle centinaia. Inoltre la legge dei grandi numeri non dice che la probabilità si bilancia dopo un elevato numero di prove, ma che all'aumentare del numero di prove eseguito, le frequenze dei due eventi si avvicinano al valore delle rispettive probabilità. Qual è l'errore del giocatore? Nel trasformare la frase che dice “all'aumentare del numero di prove” con la frase “dopo un elevato numero di prove”.
Non hanno senso neppure le previsioni basate su analisi statistiche, “numeri spia”che “annunciano” l'estrazione di ambi o terne che possono uscire più facilmente di altre (per esempio la terna 1,2 e 3 ha la stessa probabilità di uscita della terna 12,35,48); ogni volta che si gira l'urna contenente i bussolotti si ricomincia daccapo e ogni numero, ambo, terna hanno sempre la stessa probabilità di uscita, indipendente da ciò che è successo in precedenza.
Facciamo un altro esempio per chiarire meglio come un sostenitore della teoria dei numeri ritardatari si possa rovinare, insistendo nel giocare sempre lo stesso numero. Prendiamo il caso del numero 34: dopo l'ultima uscita sulla ruota di Cagliari risalente al giugno 2004 uscì il 1° aprile 2006 (si potrebbe pensare che i numeri abbiano il senso dell'umorismo...) dopo ben 206 settimane di irreperibilità.
Supponiamo di essere un giocatore “razionale che conosce” la legge dei grandi numeri e di cominciare a giocare all'inizio di gennaio del 2005: punto solo 1 € sul 34, pensando “Sono sei mesi che non esce, quindi…”, ma le mie speranze vanno deluse. Continuo a giocare (sempre 1 €, “Sono furbo, io, non voglio mica rovinarmi..) e dopo 11 estrazioni il numero continua, a sua volta, la latitanza ed io comincio a farmi due conti: se il numero esce vinco 11,23 €(il perché lo abbiamo già spiegato), che è quanto ho speso finora, quindi se voglio avere un margine di guadagno devo aumentare la posta. Decido di raddoppiare e continuare a scommettere (“prima o poi..la legge dei grandi numeri…” ). Arrivato alla sedicesima estrazione ho speso 11 €+10€=22€. Se quel benedetto numero uscisse vincerei 22, 46 €, cioè andrei a pari, ma dal momento che continua a latitare sono costretto ad alzare la posta, per poter coprire almeno le spese. E così punto 3 € e, nel frattempo con 16 estrazioni (due alla settimana, in quel periodo) sono arrivato soltanto a fine febbraio.
Penso che a questo punto il lettore cominci a capire come vanno le cose: non continuo nel calcolo, perché diventerebbe noioso. Faccio solo notare che dovrei man mano alzare la posta di 1 € e questo solo per andare praticamente a pari, senza guadagnare nulla, anche nell'eventualità che il numero uscisse, e, quindi, vincendo. E' chiaro che con un numero come il 34 (lo sapevate che per la “Smorfia” questo numero rappresenta la testa?, quella che dovrebbero usare i giocatori, aggiungo io) che non è stato estratto per 206 volte, la spesa è notevolmente salita. Il lettore tenga conto che per un altro numero, per il 53 sulla ruota di Venezia, che abbiamo già citato, quando finalmente è uscito, le vincite hanno reso sì 700 milioni di euro ai giocatori, contro però i 1200 e più giocati.
5. La probabilità condizionata
Ad ulteriore conferma della nostra tesi aggiungiamo ancora una considerazione: se si calcola che la probabilità che il 34 (o qualsiasi altro numero) esca alla 206 a estrazione condizionata dal fatto che non è uscito per 205 volte, si ritrova esattamente la probabilità che esca in una estrazione.
E' pur vero che la probabilità assoluta che un numero non esca per 205 settimane è, in effetti, molto bassa, circa otto su un milione, ma ciò non esclude che non possa succedere.
Per consentire di capire meglio, sono costretta a introdurre alcuni concetti matematici, ma, come al solito, il formalismo sarà ridotto al minimo.
Intanto dobbiamo chiarire cosa intendiamo per probabilità di un evento A condizionata da un evento B: essa è la probabilità che si verifichi A una volta che si sia già verificato B; mentre diciamo che l'evento A è indipendente dall'evento B se la probabilità del verificarsi dell'evento A non dipende dal fatto che l'evento B si sia verificato o no.
E' intuitivamente comprensibile che i due valori sono diversi.
Abbiamo ripetuto più volte che la probabilità che un numero sia estratto o meno è un evento indipendente dalle estrazioni precedenti. Ma nei siti e nelle riviste specializzate in lotto e nelle trasmissioni televisive ad esso dedicate, sedicenti esperti cercano di convincere i giocatori che ciò non è vero.
Esaminiamo l'evento A: “ esce il numero 34 alla 206 a estrazione” , esso ha come probabilità tutte le possibili cinquine, che costituiscono le estrazioni su una ruota, in rapporto a tutti i casi possibili (90 numeri), quindi
p(A) =5/90=1/18.
L'evento B , “il numero 17 non è mai uscito nelle prime 205 estrazioni” ha come probabilità quella contraria all'evento precedente e cioè 17/18, che non esca per due volte la probabilità sarà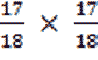 
cioè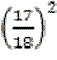 
, quindi per tre estrazioni 
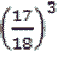e così via. Nel nostro caso specifico la probabilità che il numero 34 non esca per 205 estrazioni sarà
p(B)=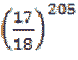
il cui valore, lo abbiamo già detto, è circa 8x10-6, quindi molto basso.
Considerare la probabilità condizionata significa studiare l'evento “ esca il 34 alla 206-ma estrazione sapendo che tale numero non è comparso nelle 205 estrazioni precedenti”; per risolvere questo problema dobbiamo ricorrere al teorema di Bayes, matematico e ministro presbiteriano britannico del 1700, sulle cui applicazioni anche in Medicina ed altre Scienze ci occuperemo più avanti.
Il teorema fornisce la seguente formula:
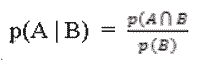
Vediamo di spiegare i vari simboli: il primo membro rappresenta la probabilità che l'evento B ha di verificarsi se si è verificato A ”, p( A ∩ B ) è la probabilità che il 34 non esce nelle prime 205 estrazioni, ma compare nella 206-ma” e vale:
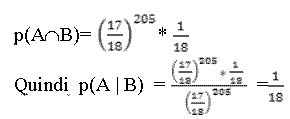
Che è la probabilità di uscita di un numero, prima calcolata; questo dimostra che il fatto che il famigerato 34 abbia fatto soffrire (e spendere) i giocatori per ben 205 estrazioni non ha alcuna influenza su ciò che è accaduto alla 206-esima.
Sono sicura che gli accaniti scommettitori non saranno affatto convinti da queste mie argomentazioni, peraltro condivise e già scritte da molti, ma io ho provato ugualmente:”Repetita iuvant” dicevano i latini.
Per chiarire ancora meglio il significato del teorema di Bayes potremmo dire che se è alta la probabilità che l'evento A sia effetto della causa B, il fatto che l'evento A si sia verificato aumenta la probabilità, anche se non dà la certezza, che a produrlo sia proprio la causa B . Viceversa, se è bassa la probabilità che l'evento A sia effetto della causa B, il fatto che l'evento A si sia verificato diminuisce la probabilità che a produrre A sia stata proprio la causa B .
6.1 Applicazioni in Medicina
Consideriamo, ora, l'applicazione della probabilità e del teorema di Bayes in Medicina occupandoci di una Scienza importante e relativamente recente, l'Epidemiologia.
Dal punto di vista etimologico questa parola è composta da tre parti, di origine greca: (epi-demio-logia) e significa “ discorso riguardo alla popolazione”; con ciò non dobbiamo credere che questa scienza studi solo malattie (infettive e contagiose) che riguardano intere popolazioni o quasi e non il singolo, al contrario “ si occupa di TUTTE le malattie ma, diversamente da altre discipline, se ne occupa esclusivamente a livello di popolazione piuttosto che di individuo”¹. In altre parole, si studiano le malattie attraverso l'osservazione della loro distribuzione e del loro andamento nella popolazione, per poter individuare i fattori che ne sono causa o che ne favoriscono la diffusione.
Paolo Vineis insegna all'Imperial College of Science, Technology and Medicine di Londra (dove è professore di Epidemiologia ambientale), all'Università di Torino e alla Columbia University di New York. Conduce da anni ricerche nel campo dell'Epidemiologia e in un'intervista afferma che l'Epidemiologia ha assunto un ruolo fondamentale in Medicina.
Per esempio, spiega Vineis, “Negli anni '30 un trattamento veniva prescritto perché il professor Tizio aveva trovato, in una piccola serie di pazienti, risultati superiori a quelli del professor Caio. In questo modo una malattia poteva avere decine di terapie diverse. Solo alla fine degli anni '40 venne introdotta l'idea di un confronto sistematico fra pazienti, di cui un gruppo veniva trattato con il farmaco da sperimentare e l'altro gruppo con un placebo e i membri dell'uno e dell'altro gruppo venivano scelti a caso”.
Uno strumento di base dell'Epidemiologia è il cosiddetto screening che consiste in una serie di esami che vengono eseguiti con lo scopo di individuare le persone a maggior rischio per una certa patologia.
In tutto ciò si inserisce il teorema di Bayes: vediamo con un esempio tratto da un articolo del dottor Marco Besozzi ( docente al Dipartimento di Medicina di Laboratorio, IRCCS, Istituto Auxologico Italiano di Milano) di spiegare “come il teorema di Bayes possa essere applicato in modo intuitivo. Si consideri un test destinato a rivelare la presenza nel siero di anticorpianti-HIV. Si assuma che questo test abbia una sensibilità del 100% (il test, quindi, è positivo nel 100% dei malati). Si assuma che questo test abbia una specificità del 99,7% (il test, quindi, è negativo nel 99,7% dei soggetti sani). Si sa che la prevalenza della positività agli anticorpi anti-HIV è del 3 per mille (nella popolazione, su 1000 soggetti presi a caso, 3sono positivi agli anticorpi anti-HIV). Supponendo di effettuare il test su 1000soggetti presi a caso i risultati saranno i seguenti: 3 soggetti presenteranno positività agli anticorpi anti-HIV, in quanto la prevalenza è del 3 per mille (veri positivi); inoltre, effettuando l'analisi su 1000 soggetti, a causa del fatto che la specificità del test è del 99,7% ci dovremo aspettare 3 positivi su1000 soggetti sani (falsi positivi). Essendo in totale 6 i soggetti positivi, e 3 i veri positivi, avremo quindi un valore predittivo del test positivo pari a 3/6, cioè un valore predittivo del test positivo pari al 50% ( p pari a 0,5).
L'esempio riportato si presta a una prima importante considerazione: il teorema di Bayes rappresenta l'unico strumento che consente di fornire una misura quantitativa, e quindi oggettiva, del valore aggiunto fornito da un test diagnostico (come un'analisi di laboratorio). Nel caso degli anticorpi anti-HIV, la differenza tra la probabilità (di essere malati) a posteriori (dopo avere effettuato il test, pari al 50%) e la probabilità (di essere malati) a priori (prima di avere effettuato iltest, pari al 3 per mille) rappresenta il valore aggiunto che il test diagnostico è in grado difornire, in termini di informazione, alla diagnosi medica. Questo fatto collega il teorema di Bayes e il processo decisionale medico alla teoria dell'informazione.
6.2 Applicazioni in Informatica
Cambiano, ora completamente argomento per occuparci di Informatica ed esattamente di quel fenomeno in cui sono incappati, più meno, tutti i navigatori della Rete e conosciuto con il nome di spamming: esso consiste nell'invio di grandi quantità di messaggi indesiderati (generalmente commerciali), attraverso l'e-mail. L'origine del nome è piuttosto curiosa, perché deriva da uno sketch tratto da una serie televisiva britannica, il Monty Python's Flying Circus.
Lo scopo dello spam è quello di inviare messaggi pubblicitari a migliaia di utenti e, siccome è inviato senza il consenso del ricevente, è in genere sgradito.
Per questo è necessario un software che permetta di “filtrare” i vari messaggi, cioè, in altre parole, occorre un “sistema”che riconosca un messaggio spam da uno normale e lo elimini, impedendogli di raggiungere il nostro indirizzo e-mail. Nell'agosto del 2002 è apparso un articolo di Paul Graham dal titolo " A Plan for Spam" dove descrive un metodo innovativo nell'affrontare il problema che si basa sulla formula di Bayes molto più efficace di quello usato dai cosiddetti filtri automatici. Il giornalista Paolo Altissimo spiega in modo chiaro ed esaustivo, nel sito della casa Apogeo (www.apogeonline.com) le principali differenze tra i due sistemi. Il primo, quello automatico, si basa sulla presenza nel testo del messaggio di parole facenti parte di un elenco segnalato dall'utente e che, quindi, se presenti nel testo, fanno sì che il messaggio venga bloccato.
Questo metodo presenta, però, spiega Altissimo, degli inconvenienti: infatti può diventare o poco efficace, perché gli spammer riescono ad aggirare l'ostacolo del riconoscimento della parola (cambiando per esempio le dimensioni un carattere) oppure troppo restrittivo. L'esempio che Altissimo riporta mi sembra particolarmente significativo: se abbiamo nel nostro elenco di parole da escludere la parola porno (gli spam su tale argomento sono molto diffusi) verranno sì cestinati tutti i messaggi che contengono questa parola, ma se “un vostro amico vi manda un' e-mail supplicando aiuto per debellare il dialer di un sito porno che gli ha infettato il computer, il suo messaggio verrà cestinato come spam” e voi rischiate di perdere un amico.
Invece, il filtro bayesiano si basa su un principio di classificazione diverso che fa uso di un teorema sulla probabilità il cui autore, ironia della sorte, è vissuto circa trecento anni fa.
Il programma-filtro analizza un insieme di “messaggi tipo” che l'utente indica come spam e calcola “automaticamente la frequenza d'uso delle varie parole contenute, includendo anche i codici HTML e i dettagli delle intestazioni (header)”. Si forma una “classifica” di presenze per ogni parola: si attribuisce un punteggio a determinate parole e se il punteggio supera un certo limite minimo vengono classificate come Spam. .
Quindi, se una parola con alta frequenza è presente nel testo di un dato messaggio è probabile, ma non sicuro, che questo sia spam. La sicurezza è ottenuta valutando la frequenza “complessiva” delle varie parole che sono contenute nel testo. Cosa significa? Significa che se un'e-mail contiene un termine giudicato “una parola ad alto rischio spam ma per il resto è costituito da parole poco usate dagli spammer, non viene classificato come spam” e, quindi, il rischio di “falsi positivi” (concetto già incontrato in Medicina) è molto basso. Infatti ci sono parole, fa osservare Altissimo, che gli spammer non possono fare a meno di usare se vogliono propagandare efficacemente il loro prodotto e, sostiene Graham, in genere il loro frasario è molto limitato e, questo fatto, rappresenta il loro tallone d'Achille.
Dopo queste premesse è chiaro che un messaggio come quello indicato nell'esempio non verrebbe cestinato.
Alcuni provider, invece, si difendono costituendo delle liste, le cosiddette blacklist, che contengono Ip o indirizzi considerati fonti di spam.
Esistono, come è facilmente immaginabile, due scuole di pensiero a favore dell'uno o dell'altro metodo; non ci addentriamo in questa analisi perché ci allontanerebbe troppo dall'argomento principale, concludiamo, perciò, dicendo che la lotta allo spam è sempre aperta e fior di esperti elaborano sistemi sempre più sofisticati per liberarci di questa posta indesiderata.
7. Il dilemma di Monty Hall
La probabilità è applicata anche nelle strategie militari, ma la guerra non è un argomento che, come si dice, è nelle “nostre corde” e così ho pensato di terminare il capitolo in modo più divertente: propongo due curiosi problemi in cui il calcolo della probabilità permette di arrivare ad una soluzione che, in certo senso, va contro l'intuizione comune. Il primo è noto come “il dilemma di Monty Hall” ed è legato ad un gioco a premi americano Let's Make a Deal e trasmesso dalla Tv americana negli anni 90 .
Intanto il nome viene da quello del conduttore dello show, Maurice Halprin, noto con lo pseudonimo di Monty Hall. In questo gioco, vengono mostrate a un giocatore tre porte chiuse; al di là di una c'è un'automobile e dietro ciascuna delle altre due si nasconde una capra. Il giocatore sceglie una porta, ma non la apre; il conduttore dello show (che conosce ciò che si trova dietro ogni porta) deve aprire un'altra porta, e poiché conosce la disposizione dei premi, ne apre una che nasconde la capra. A questo punto il presentatore al giocatore la possibilità di cambiare la propria scelta iniziale, (oppure di tenersi il premio nascosto dietro alla porta da lui scelta) passando all'unica porta restante. La domanda è, quindi: conviene cambiare o no? Il giocatore può ragionare in questo modo: “So che in una delle due porte rimaste, tra cui quella che ho scelto inizialmente, c'è certamente l'automobile, quindi la probabilità è pari, per entrambe le porte, ad ½. Perciò è indifferente cambiare o no”.
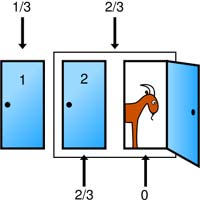
La questione, però, non finì così semplicemente. Infatti essa fu proposta nel 1990 nella popolare rubrica di domande e risposte “Chiedilo a Marylin” della rivista americana Parade dal Sig Craig F. Whitaker (Columbia, Maryland). La rubrica era tenuta da Marylin vos Savant, personaggio non certo di poco conto, in quanto presente nel Guinness dei Primati per il suo altissimo Q.I.(228)
Marylin rispose che la soluzione prima fornita è errata e che al concorrente conviene comunque cambiare, in quanto la probabilità di vincita passa da ½ a 2/3.
Questa risposta, però, non soddisfò i suoi lettori che la subissarono di lettere di proteste (tra cui, pare, molti matematici insigniti del Ph.D, titolo equivalente al nostro dottorato di ricerca) che contestavano la soluzione della Savant.
Persino Paul Erdos, uno dei più grandi matematici del '900 disse «Impossibile. Non può fare differenza il cambiare la porta» («L'uomo che amava solo i numeri», P.Hoffman) e dall'Università della Florida le scrissero: "Lei sembra avere difficoltà a cogliere gli aspetti fondamentali della teoria della probabilità... C'è già abbastanza ignoranza Matematica nel paese, senza che si metta a creare confusione anche la persona con il più alto QI del mondo!"
Marylin non cedette e dimostrò di essere nel giusto con un metodo molto efficace; costruì una tabella con i sei casi possibili: l'auto è dietro la porta A, B o C e il giocatore non cambia la scelta oppure, l'auto è dietro A, B o C e il giocatore cambia .
Ne risulta che se si sostituisce si vince in due casi su tre. Se non si cambia in un caso su tre. Nel caso in cui l'auto sia dietro la porta A la tabella potrebbe essere come la seguente. (Si tenga presente che prima della proposta di cambio il presentatore apriva una porta che nascondeva la capra)
| Porta scelta | Il giocatore cambia | Il giocatore non cambia |
| A | Perde | Vince |
| B | Vince | Perde |
| C | Vince | Perde |
Per chiarire ulteriormente la situazione riassumiamo i risultati delle due strategie possibili con le rispettive probabilità teoriche di vincita:
- mantenere la scelta iniziale (P = 33%);
- scegliere la porta non aperta (P = 67%).
8. Il paradosso del compleanno
Nella speranza che il lettore incominci ad appassionarsi a questo tipo di problema, ne propongo un altro, altrettanto curioso e in apparente contraddizione con il nostro senso comune, tanto che, a volte, si fatica a crederci anche se viene dimostrato: il paradosso del compleanno (o problema del compleanno ) definito nel 1939 da Richard von Mises. Il paradosso afferma che la probabilità che due persone in un gruppo compiano gli anni nello stesso giorno è largamente superiore a quanto potrebbe dire l'intuito: infatti già in un gruppo di 23 persone la probabilità è circa del 51%; con 30 persone essa supera il 70%, con 50 persone tocca addirittura il 97%, considerando un gruppo di 60 si arriva praticamente all'evento certo.
Richard von Mises (Lemberg, 19 aprile 1883 – Boston, 14 luglio 1953) è stato un matematico, ingegnere e accademico austriaco naturalizzato statunitense. E' conosciuto per i suoi importanti contributi nel campo della Meccanica dei fluidi, dell'aerodinamica, dell'aeronautica, della statistica e di teoria della probabilità, che è il campo in cui trova appunto applicazione il suo paradosso.
Per capire la soluzione del problema utilizziamo la spiegazione di Martin Gardner, matematico americano morto nel1914, il quale nel suo libro Probability paradoxes, fornisce un semplice procedimento che permette di calcolare la suddetta probabilità.
Supponiamo di prendere in considerazione il fatto che due persone non compiano gli anni lo stesso giorno e calcoliamo la probabilità contraria: essa vale 1- 1/365=364/365 (dato che vi è una sola possibilità su 365 che il compleanno di una persona coincida con quello di un'altra).
Allo stesso modo eseguiamo il calcolo se le persone sono tre (363/365), sono quattro (362/365) fino a 24 persone che risulta essere 342/365. Moltiplicando tra loro le 23 frazioni si ottiene un risultato che semplificato dà 23/50, ciò significa che su 24 persone la probabilità che due di esse festeggino il compleanno lo stesso giorno è di 27/50, cioè del 54%. A conferma di questo risultato che, forse, ci sorprende un po', vorrei riportare una statistica pubblicata sul sito Espresso Web in un articolo del 19 gennaio 2008: esaminando le date di nascita e di morte di Presidenti americani (43 date di nascita e 39 date di morte) si vede che Polk e Harding nacquero il 2 novembre mentre Carter e Heisenhower il 14 ottobre; Truman e Ford morirono il 26 dicembre, Polk e Buchanan il 15 giugno e ben tre presidenti, Jefferson, Adams e Monroe, morirono il 4 luglio.
