Il mistero di Archimede

Ironia della sorte! Democrito è l'unico filosofo citato in una sua opera da Archimede ed ha scritto cose di Matematica, mentre né Platone né Aristotele vengono citati dallo stesso, né hanno scritto cose di Matematica, ma solo testimonianze, sparse nei loro scritti e molte volte confuse (per un severo giudizio su Platone, testimone di cose matematiche, rimando ad un giudizio di Peano, che certamente di Matematica se ne intendeva, come di filologia greca, in Opere, vol. III, Ed. Cremonese, 1958, p.249 ), eppure vengono considerati gli ispiratori di Archimede!

Nel 212 a .C. durante il saccheggio di Siracusa da parte delle armate romane guidate dal console Marcello, moriva, per mano di un soldato romano, Archimede di Siracusa; così narra Plutarco, il quale aggiunge che il console Marcello, davanti alla devastazione di Siracusa, “non poté nascondere la compassione e il dolore che provava in cuor suo a veder cancellato in un attimo quel regno di felicità e di splendore” (1).

Ma Siracusa non era solo “regno di felicità e di splendore”. E' lì che con Archimede la scienza antica raggiunge le sue vette più alte.

Il postulato di Archimede sta alla base dei moderni trattati di calcolo (2).

Nel Cinquecento e nel Seicento, con la scoperta e lo studio delle opere di Archimede, si diffonde intorno alla sua figura una certa aria di “ mistero”. Studiato da Galileo “con infinito stupore” (3) e ammirazione, venerato da tutti gli scienziati di quel tempo per le sue ardite invenzioni e preso come modello di rigore, Archimede fa sorgere sulla sua opera la convinzione, che diventa anche leggenda, “che egli abbia di proposito ricoperto le tracce della sua investigazione, come se avesse sepolto per la posteriorità il segreto del suo metodo di ricerca” (4).

E' solo nel 1906, grazie al filologo danese J.L.Heiberg, editore delle opere di Euclide e Archimede, che si dirada l'aria di mistero. In un antico palinsesto ritrovato a Costantinopoli presso il monastero del Santo Sepolcro lo studioso intravede scritti di Archimede, ai quali era stato sovrapposto un eucologio.Viene alla luce una importante opera di Archimede, indirizzata ad Eratostene di Alessandria, in cui sono dimostrati alcuni teoremi meccanici, attraverso i quali Archimede svela come sia riuscito a calcolare l'area del segmento parabolico, il volume della sfera, l'area della sua superficie, i volumi del cono e del cilindro, …

Così Archimede scrive ad Eratostene:

“Vedendoti poi diligente ed egregio maestro di filosofia, e tale da apprezzare anche nelle matematiche la teoria che (ti accada di considerare), decisi di scriverti e di esporti nello stesso libro le caratteristiche di un certo metodo, mediante il quale ti sarà data la possibilità di considerare questioni matematiche per mezzo della meccanica . E sono persuaso che questo (metodo) sia non meno utile anche per la dimostrazione degli stessi teoremi. E infatti alcune delle (proprietà) che a me dapprima si sono presentate per via meccanica, sono state (da me) più tardi dimostrate per via geometrica, poiché la ricerca (compiuta) per mezzo di questo metodo (del metodo meccanico) non è una (vera) dimostrazione: è poi più facile, avendo gia ottenuto con questo (metodo) qualche conoscenza delle cose ricercate, compiere la dimostrazione, piuttosto che ricercare senza alcuna nozione preventiva. Perciò di quei teoremi dei quali Eudosso trovò per primo la dimostrazione intorno al cono e alla piramide, (cioè) che il cono è la terza parte del cilindro e la piramide è la terza parte del prisma, aventi la stessa base e altezza uguale, non piccola parte (del merito) va attribuito a Democrito, che per primo fece conoscere questa proprietà della figura suddetta, senza dimostrazione ” (5).

Con questa testimonianza diretta di Archimede e dall'esame dei “teoremi meccanici” si dipana il mistero di Archimede, essendosi trovata la via segreta per la ricerca dei suoi notevoli risultati.

I matematici di tutti i tempi sono sempre rimasti ammirati dal rigore delle dimostrazioni di Archimede, che riusciva ad utilizzare in modo mirabile il cosiddetto “metodo di esaustione” (6); metodo che, molto probabilmente, era stato introdotto da Eudosso di Cnido per evitare l'uso dei cosiddetti “indivisibili”, i quali, ancora ai tempi di Archimede, erano giudicati inutilizzabili in Matematica a causa forse dei “paradossi di Zenone”. Nulla sappiamo di Eudosso circa la sua concezione degli indivisibili; vero è che il metodo di esaustione evita il loro uso.

Conserviamo invece una dura requisitoria logico-filosofica contro gli indivisibili da parte di Aristotele.

Egli nega che la linea possa comporsi di punti, la superficie di linee e il solido di superfici. Il continuo degli enti geometrici, secondo Aristotele, si compone di grandezze sempre divisibili.

In un passo del “De Generatione” Aristotele si chiede: “ Se queste grandezze originarie sono indivisibili, dobbiamo noi identificarle con corpi, come sostengono Democrito e Leucippo, oppure come superfici come si afferma invece nel Timeo? ”, ma subito dopo afferma: “Quest'ultima alternativa – quella cioè secondo cui si opera la dissoluzione delle cose fino alla superficie – è assurda, come abbiamo detto altrove; perciò è più conforme a ragione considerare indivisibili i corpi quantunque anche questa soluzione comporti un notevole numero di assurdità” (7). L'assurdo in cui cade, secondo Aristotele, chi ammetta grandezze atomiche o indivisibili (chiaramente si riferisce a Democrito) è quello di fare scomparire qualunque grandezza da esse composta, essendo necessariamente nulle le grandezze atomiche.

Aristotele nega che possano esistere grandezze infinitesime di forze, dF, come oggi scriviamo, tali che sommate possano superare qualunque resistenza data, anche grande quanto si vuole, ma pur sempre finita. Scrive infatti nella sua opera La Fisica:

“Se l'intera forza ha attuato il movimento secondo tanta quantità di lunghezza, la metà di essa non attuerà il movimento secondo altrettanta quantità né in un tempo qualsivoglia; se fosse altrimenti un uomo solo muoverebbe la nave, qualora venissero numericamente divise la forza di quelli che la tirano a secco e la lunghezza secondo cui tutti la muovono ” (ivi , VII, 5, 250a, 15-20).

Aristotele nega che un punto possa descrivere, muovendosi, un segmento di retta o una curva.

Scrive ancora a questo proposito nell'opera citata:

“Risulta chiaro che non possono muoversi né il punto né alcuna altra cosa indivisibile ” (ivi, VI; 241a, 5-10).

Gli indivisibili, espulsi, grazie ad Aristotele, dalla Fisica e dalla Geometria, hanno assunto nel tempo un considerevole valore euristico nella ricerca matematica e fisica, come si è potuto verificare nei secoli successivi.

E' proprio di loro, secondo la testimonianza dello stesso Archimede, che si era già servito Democrito, e pure di questi Archimede si avvale nel suo “metodo meccanico” insieme ai suoi teoremi sull'equilibrio dei corpi, per raggiungere i suoi brillanti risultati.

Il Dijksterhuis non ha dubbi sul fatto che Archimede, quando affermava che i risultati conseguiti col “metodo meccanico” non costituivano una vera dimostrazione, si riferisse non tanto all'uso dei teoremi meccanici, di cui si era già avvalso nella Quadratura della parabola ( an official publication satisfying all requirements of exactness ), quanto piuttosto all'uso degli indivisibili ( the mathematical definiency is exclusively a consequence of the use of indivisibles ) (8).

Dello stesso parere è anche lo storico della Matematica Boyer, secondo il quale, tra l'altro, “Archimede di Siracusa ha mostrato due nature, poiché ha mescolato la immaginazione fortemente trascendentale di Platone con il procedimento meticolosamente corretto di Euclide” (9). Si è scritto inoltre che con la scoperta del “metodo”, Archimede “ci fa guardare dentro la sua officina meccanica” (10). Secondo noi, con la scoperta del “metodo”, Archimede ci fa guardare dentro la sua officina filosofico-epistemologica, se è vero quanto abbiamo prima detto. E in tale officina non troviamo più né Platone né Aristotele, ma solo Democrito con il suo atomismo fisico e geometrico.

Per Archimede c'è una corrispondenza tra atomismo fisico e atomismo geometrico; lo stesso rapporto che vale per linee geometriche vale anche per le linee fisiche, immaginate omogenee, che si fanno equilibrio in una leva. Anzi possiamo dire che la sua Fisica e la sua Geometria sono costruite in polemica con Platone stando al seguente passo di Plutarco: “Gli iniziatori della meccanica, scienza seguita con interesse e a tutti nota, furono Eudosso ed Archita, i quali comunicarono un grande fascino alla geometria mediante l'eleganza dei suoi procedimenti.

Essi diedero ai problemi che non offrivano possibilità di soluzione con un procedimento soltanto logico e verbale il sostegno di schemi visivi e meccanici. Ad esempio nella soluzione del problema di due rette medie proporzionali, elemento necessario alla composizione di molte figure, entrambi gli scienziati ricorsero a mezzi meccanici, servendosi delle medie proporzionali che certi strumenti ricavavano da linee curve e da segmenti. Platone rimase indignato da questo modo di procedere e polemizzò coi due matematici, quasi che distruggessero e corrompessero ciò che vi era di buono nella geometria; in tal maniera essa abbandonava infatti i concetti astratti per scendere nel mondo sensibile, ed usava anch'essa oggetti che richiedevano ampiamente un grossolano lavoro manuale. La meccanica fu così separata e si staccò dalla geometria; per molto tempo la filosofia l'ignorò ed essa divenne una delle arti militari” (11).

Archimede viola il divieto platonico di legare Meccanica e Geometria. Sorge anzi, dalla lettura di questo brano, il fondato sospetto che già lo stesso Eudosso abbia iniziato l'uso del “metodo meccanico” per la soluzione dei problemi geometrici, ma che ne fu bloccato dalla proibizione platonica.

Archimede viola e sfida pure il divieto di Aristotele che grandezze infinitesime di forze possano sommandosi superare qualunque resistenza finita, pur grande quanto si voglia, introducendo il concetto di momento di una forza con la sua legge sulla leva.

In funzione antiaristotelica si può interpretare il famoso episodio della nave raccontato da Plutarco.

“Archimede scrisse al re Ierone, di cui era parente ed amico, che era possibile muovere un dato peso con una data forza; e si dice che, pieno di entusiasmo per la forza della propria dimostrazione, affermò che, se avesse avuto un'altra terra, passato su quella, avrebbe potuto muovere questa. Ierone, meravigliato, gli chiese di tradurre in pratica questo problema geometrico e di mostrargli qualcosa di gran mole mosso da una piccola forza. Archimede fece tirare in secco con grande fatica e con grande impiego di molti uomini una nave da carico a tre alberi della flotta reale e vi fece salire molti uomini insieme con il carico che era solita portare; poi, stando seduto lontano, senza sforzo, ma muovendo con una mano un sistema di pulegge, fece avvicinare la nave dolcemente e senza scosse come se corresse sul mare ” (12).

Archimede, descrivendo come si origina la sua spirale, dal movimento di un punto su un segmento di retta che si muove a sua volta in circolo, attorno ad un suo estremo fissato, viola ancora il divieto aristotelico suddetto.

Non si capisce poi da dove il Dijksterhuis abbia tratto la convinzione che la lettura ad Eratostene “sia privata” (13), se leggiamo nella stessa “ ho voluto quindi, avendolo scritto, pubblicare quel metodo, sia perché ne avevo parlato già prima sia perché sono convinto che porterà non piccola utilità alla matematica: confido infatti che alcuni dei matematici attuali, o dei futuri essendo stato loro mostrato questo metodo, ritroveranno altri teoremi da noi non ancora escogitati ” (14).

Non è invece da ritenere che Archimede abbia maturato la convinzione che la Filosofia degli indivisibili non abbia niente di che vergognarsi, né di che nascondersi, essendo essa perfettamente conciliabile con il metodo di esaustione di Eudosso, e che porta a fecondi risultati nel campo della scienza?

Il “mistero” della scomparsa del “metodo” di Archimede durante i secoli, e qui ci sia consentita una amara considerazione, non richiama il “mistero” della scomparsa della vastissima produzione di Democrito, il quale, come si sa, non viene mai citato da Platone, a differenza di tutti gli altri cosiddetti “presocratici”?

Per concludere, Archimede non è solo un grande matematico o un grande fisico, ma è anche un grande filosofo che ha una concezione organica dell'universo.

NOTE

(1) Plutarco, Vite parallele , Mondatori, 1965, vol. III, p.335

(2) Archimede enuncia il suo postulato in termini geometrici: “ Che inoltre per le linee disuguali e per i solidi disuguali, il maggiore superi il minore di una grandezza tale che addizionata a se stessa possa superare qualunque grandezza data, tra quelle che si possono paragonare tra loro”(Archimede, Opere, Sulla sfera e il cilindro , postulato V).Oggi esso viene assunto come un postulato del sistema dei numeri reali, dopo l'aritmetizzazione dell'Analisi nella seconda metà dell'Ottocento con Cantor, Dedekind e Weierstrass: “Se a e b sono due numeri reali positivi del sistema, e a < b , esiste sempre un numero reale n tale che sia n a > b.”

(3) Cfr. G. Galilei, Opere , Utet, Torino, 1964, Vol. II, p. 613.

(4) Così si esprimeva il matematico Wallis nella sua Arithmetica infinitorum del 1665.

(5) Archimede, Opere , Utet, 1974, p. 572.

(6) Per il metodo di esaustione cfr. Appendice.

(7) Aristotele, Della generazione e della corruzione , Laterza, Bari, 1973, p.10.

(8) Dijksterhuis, Archimedes , Copenhagen , 1956, p.319.

(9) Cfr. C.B. Boyer, The Concepts of the Calculus , N. York , 1939, p. 48.

(10) La frase riportata in Archimede, Opere , è dello storico della Matematica H.G.Zeuthen.

(11) Plutarco, op. cit. , p. 331.

(12) Ib ., pp. 432-433.

(13) Op. cit. , p. 316.

(14) Op.cit. , p. 573.

Appendice

IL METODO DI ESAUSTIONE

Con il metodo di esaustione si dimostra che le misure di due grandezze A e B sono uguali, m(A) = m(B), se vale quanto segue:

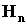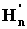Date le due grandezze omogenee A e B , si possono costruire due classi H e H' di grandezze omogenee ad A e B, i cui elementi indichiamo rispettivamente con e , tali che:

per ogni E (numero reale positivo), esiste un n tale che A – 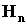< E;

per ogni n, 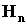 minore o uguale a B;

1' per ogni E, esiste un n tale che 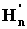– A < E;

2' per ogni n, B minore o uguale a .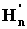

Allora m(A) = m(B).

Dimostrazione: sia A > B e poniamo A- B = E; per la 1 si ha A- 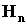< E = A – B.

Ne segue pertanto che B < 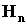. Ma ciò è assurdo, poiché si contraddice l'ipotesi 2 che B sia maggiore o uguale 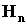. Allora A non può essere maggiore di B.

Ma non può essere neppure A< B.

Infatti poniamo B – A = E; per la 1' vale 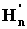– A < E = B - A.

Si ha pertanto 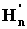< B in contraddizione all'ipotesi 2' che vuole B minore o uguale a .

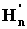Se non valgono allora né A>B né A < B, ne segue che A = B.

Archimede dimostra per esempio con il metodo suddetto che m (C) = m(T), cioè che l'area del cerchio C è uguale all'area del triangolo T con base la circonferenza del cerchio e altezza il suo raggio. In questo caso basta sostituire C ad A e T a B , 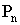 a 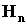( 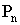sono le aree dei poligoni iscritti al cerchio) e  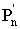a 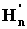( 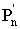sono le aree dei poligoni circoscritti al cerchio).