La lingua nell'apprendimento della Matematica da parte dei ragazzi cinesi. Una ricerca di didattica della Matematica
Abbiamo ricordato Filippo Spagnolo, scomparso improvvisamente nello scorso mese di marzo, con l'articolo "Perché mi sono interessato alle questioni cinesi". Della stessa ricerca pubblichiamo ora la seconda parte.
Inquadramento della problematica di ricerca: aspetti logico-argomentativi
Uno dei problemi chiave dell’insegnamento/apprendimento delle matematiche in situazione di multiculturalità è certamente quello di affrontare lo studio della disciplina e delle problematiche riferite al suo processo di insegnamento/apprendimento attraverso considerazioni di carattere sociale, culturale, antropologico, geografico ecc., trattando quindi in maniera diretta non soltanto le problematiche strettamente riferite ai contenuti disciplinari (ambiti di indagine privilegiati per la ricerca), ma anche quelli che in molti casi possono definirsi come gli aspetti storico-epistemologici della disciplina discussa in aula con gli allievi.
La ricerca nazionale ed internazionale in didattica della Matematica, negli ultimi anni, si è sempre più interessata alla problematica trattata e gli studi condotti in Italia e all’estero hanno posto l’accento sulla necessità di riflettere sulle questioni riguardanti le Matematiche elementari in una visione quanto più ampia possibile, alla luce di una scuola sempre più “diversificata”, multiculturale e globalizzata.
Quale didattica disciplinare nella classe del terzo millennio? Quale formazione matematica? Quali saperi? E quindi… quale matematica trasmettere agli allievi? Quali contenuti ritenere più utili per un apprendimento condiviso? Come relazionare questi alle culture presenti in classe?
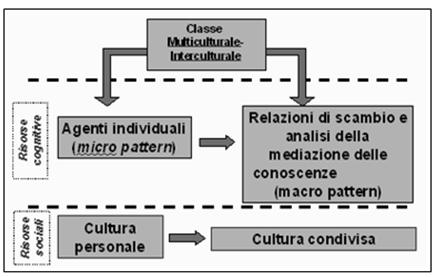
Volendo schematizzare la complessa situazione degli “agenti” che intervengono oggi in classi con allievi di differenti culture, si potrebbe utilizzare, seppur in una prima approssimazione lo schema raffigurato accanto (Di Paola & Spagnolo, 2010) che evidenzia micro e macro pattern che interagiscono all’interno del contesto classe sul sapere disciplinare in oggetto.
Fig. 1
Questo secondo articolo, nato da un approfondimento del primo, cercherà di discutere queste problematiche affrontate dal G.R.I.M. di Palermo presentando, seppur brevemente, i risultati di ricerca ottenuti dalla fine degli anni ’90 sino alla pubblicazione del volume: F. Spagnolo & B. Di Paola, (2010), European and Chinese cognitive styles and their impact on teaching mathematics (Springer, Studies in Computational Intelligence, Vol. 277). La produzione scientifica realizzata si inserisce in questo senso a metà strada tra i lavori di ricerca di didattica della Matematica riferiti ad un quadro teorico di natura etno-matematico (D’Ambrosio, 2002) e quelli riguardanti l’insegnamento/apprendimento in situazioni di multiculturalità. Nello specifico, nella ricerca si è focalizzata l’attenzione sulle relazioni (analizzate anche attraverso un continuo riferimento alla storia della Matematica), tra lingua naturale e forme argomentative rilevanti per l’apprendimento della disciplina, nella cultura orientale (cinese) ed occidentale (europea). Il binomio Lingua Naturale-Matematica, elemento chiave per la
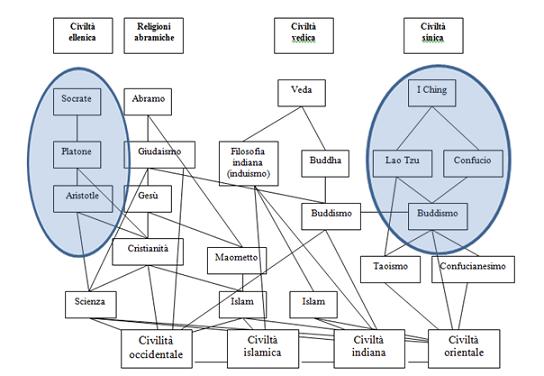
ricerca condotta, è sempre stato un tema piuttosto dibattuto in letteratura e non soltanto in didattica della Matematica. Il difficile rapporto esistente tra l’espressione linguistica quotidiana (poco formale ed imprecisa) e il contesto matematico, rigoroso e formalizzato, è stato ed è un tema ampiamente studiato in ricerca. Uno dei problemi aperti, sottolineato negli ultimi anni a livello nazionale ed internazionale è stato però quello di interpretare i risultati ottenuti in condizioni di multiculturalità e nello specifico in presenza di allievi di cultura cinese. Questi infatti hanno, soprattutto nello studio dell’Algebra (ed in parte anche in Geometria) messo in crisi quelli che erano i risultati stabili della ricerca. Ma...perché gli studenti cinesi sono più bravi in Matematica? La nostra ricerca ha cercato di riflettere su questo aspetto attraverso uno studio epistemologico della cultura cinese comparandola a quella occidentale per quanto attiene agli schemi logico argomentativi messi in atto dagli studenti della scuola dell’obbligo nelle attività del Problem Solving algebrico e geometrico. Volendo schematizzare, potremmo riassumere così le coordinate culturali prese in esame:
Fig. 2
In questo senso, il framework culturale riferito da un lato alla terna Confucio/Tao/Buddha e dall’altro a Socrate/Platone/Aristotele in relazione alle relative virtù cardinali è risultati centrale nel processo di studio e comparazione dei fenomeni di insegnamento/apprendimento dei due Paesi.
Le indagini sperimentali che il G.R.I.M. ha condotto sul tema in oggetto si sono rivolte essenzialmente a due temi tra loro connessi e sviluppati attraverso indagini sperimentali collegate a livello teorico/metodologico. Il primo fa riferimento a un lavoro sperimentale (Ajello-Spagnolo-Xiaogui, 2005; Spagnolo 2005) condotto parallelamente a Palermo e a Nanjing (in Cina), il secondo, come accennato nel primo articolo, si riferisce ad un lavoro di tesi di dottorato sviluppato in classi multiculturali a Palermo1.
Il primo tema di ricerca, non facendo riferimento ad un contenuto matematico specifico, si è posto come obiettivo quello di presentare situazioni/problema tipiche del pensiero matematico con particolare attenzione alle problematiche logico-linguistiche e argomentative degli allievi. Il riferimento più significativo della ricerca è stata quindi l’indagine sugli schemi di ragionamento orientali in relazione a quelli europei con strumenti di tipo storico epistemologico. Altrettanto importante, per lo studio delle contingenze sperimentali, è stata in questo senso l’analisi epistemologica relativa all’uso delle logiche sottese in relazione alle lingue naturali utilizzate degli allievi coinvolti sperimentalmente (cinesi ed italiani).
Il secondo tema di ricerca, mirando essenzialmente all’analisi dei processi cognitivi messi in luce dagli allievi di differenti ordini scolastici (scuola primaria e secondaria di secondo grado) in relazione ad un contesto matematico specifico quale il passaggio dal pensiero aritmetico al pensiero algebrico, si proponeva di studiare attraverso differenti indagini sperimentali9, il “comportamento” degli allievi cinesi e italiani. Particolarmente significativo per il lavoro di comparazione10, è stato l’utilizzo da parte degli allievi di differenti ordini scolastici e di differente etnia, inseriti nello stesso gruppo classe, della concezione di variabile come incognita e relazione–funzionale e di parametro (Arzarello, Bazzini, Chiappini, 1994; Malisani, 2005). In questo senso si è approfondita l’ipotesi discussa nel primo articolo in relazione alla quale la lingua naturale cinese scritta potesse, in funzione proprio della sua composizione interna, favorire negli allievi cinesi determinate competenze chiave per il pensiero algebrico (quali il concetto di variabile e il processo di generalizzazione all’interno della struttura linguistica letta attraverso una possibile definizione di un complesso sistema di tipo “parametrico” legato al ruolo del “radicale”).
L’ipotesi di ricerca unificante i due temi è stata così formulata:
H1: Le differenze e le analogie nella storia delle culture11 orientale e occidentale hanno un equivalente anche nelle differenze e analogie tra gli schemi di ragionamento riscontrabili oggi in situazioni di insegnamento /apprendimento delle matematiche.
Questa si è poi diversificata nei due temi di ricerca attraverso delle sottoipotesi più specifiche su argomentare e congetturare da un lato e sulla specificità del pensiero aritmetico/algebrico dall’altro.
Fig. 3
In linea con quanto osservato con l’esperienza di Tong, per poter falsificare le ipotesi di ricerca, per entrambi i temi sono stati utilizzati i seguenti riferimenti paradigmatici:
1 - analisi storica e storico-epistemologica del pensiero matematico, per quanto riguarda lo studio delle differenze degli schemi di ragionamento (argomentare, congetturare e dimostrare) e della tradizione algebrica nell’antichità. Quest’ultima è stata letta in uno sguardo d’insieme attraverso una possibile “comparazione” tra gli Elementi di Euclide, come canone di riferimento per la tradizione Matematica occidentale e il Jiuzhang Suanshu con i commentari di Liu Hui (263 d.C.) e Li Chunfeng (656 d.C.) per quella cinese. I riferimenti teorici sono stati principalmente in questo senso i lavori di Cai (2007), Chemla (2001, 2004), D’Ambrosio (2002), Leung (2006), Needham (1981) e Nisbett (2001, 2003).
2 - analisi linguistiche e neuroscientifiche sulle lingue alfabetiche e ideografiche per una comparazione degli aspetti cognitivi relativi alla lingua naturale di origine degli allievi e quindi possibili ricadute sull’apprendimento della Matematica; studio delle meta-regole di composizione della lingua scritta cinese in relazione ad alcuni aspetti culturali propri dell’etnia cinese come lo yīn-yáng taoista e a aspetti che possono ritrovarsi negli schemi di ragionamento algebrico e pre-algebrico;
3 - analisi sperimentale di situazioni/problema attraverso l’approccio della Teoria delle Situazioni Didattiche (Brousseau, 1997)
4 - analisi di casi attraverso lo strumento metodologico dell’intervista individuale.
Contingenze sperimentali e osservazioni conclusive sulle indagini di ricerca condotte
La ricerca in didattica, per sua natura non è mai conclusiva, nel senso che non riesce a procedere per prove. Si deve accontentare di evidenze. E’ necessario definire cosa conta, cioè quali comprensioni interessano, quali comportamenti, per quali studenti, sotto quali condizioni e quali quindi le evidenze in relazione a queste variabili significative. La ricerca in didattica non offre quindi risposte esatte ma strumenti, tracce, opportunità di riflessioni e metodi. In questo senso la natura stessa della ricerca è fornita dal processo secondo il quale si esplica e si dichiara attraverso una serie di caratteristiche peculiari quali il potere descrittivo; quello di esplicazione; la definizione dello scopo, il potere predittivo; il rigore e la specificità del metodo; la falsificabilità e la replicabilità della ricerca; le fonti multiple di evidenza.
Certamente non sempre è possibile soddisfare tutti questi requisiti; condizione necessaria trasversale è però in generale uno studio approfondito dei processi di pensiero delle fasi di insegnamento/apprendimento contestualizzate ad un contenuto disciplinare fondante.
Il lavoro di ricerca condotto dal G.R.I.M. ha cercato, in questo senso, seppur in prima approssimazione, di discutere negli anni alcune evidenze sperimentali relative ad un campo disciplinare di indagine a nostro parere significativo, come quello algebrico e pre-algebrico, letto, in una prospettiva etno-matematica attraverso una discussione critica di possibili riferimenti epistemologici-culturali significativi per le fasi di insegnamento/apprendimento del contenuto matematico trattato.
Analizzare gli stili cognitivi attraverso un approccio socio-culturale evidenziando quelle che possono essere gli schemi di ragionamento, i comportamenti, le credenze e le concezioni riguardo all’acquisizione di un particolare concetto, uno specifico sapere, è certamente un’operazione complessa, a maggior ragione nel nostro caso considerato il sistema di riferimento analizzato (sistema culturale occidentale/italiano - sistema culturale orientale/cinese) ma può essere la chiave per una didattica più attenta alle diverse abilità e quindi all’integrazione reciproca; “bisogno” ormai sentito da tutti i soggetti che operano nella scuola.
La prima indagine sperimentale
Relativamente al primo tema, i dati raccolti relativamente a questa fase della ricerca (Ajello-Spagnolo-Xiaogui, 2005; Spagnolo 2005) sembrano confermare per gli allievi cinesi un comportamento di tipo fortemente pragmatico, concreto, messo in luce da un ragionamento di tipo algoritmico procedurale strettamente connesso al un pensiero olistico sulla codifica e decodifica delle informazioni presentate nelle varie situazioni/problema. Questi, nella fase di argomentazione e congetturazione matematica, evidenziano generalmente un approccio euristico per tentativi ed errori, finalizzato alla ricerca di un “algoritmo fondamentale” come strumento di dimostrazione5. Per gli allievi cinesi, l’argomentazione e l’organizzazione dei ragionamenti avviene per gerarchizzazione dei modelli di ragionamento (modelli e sottomodelli come insiemi e sottoinsiemi) che sembrano far riferimento a implicazioni fuzzy. Il ragionamento tipico messo in luce dagli allievi italiani è invece di tipo ipotetico-deduttivo attraverso una catena finita di congiunzioni contestualizzate ad una logica bivalente. I due differenti punti di vista sono stati opportunamente confortati con l’analisi storico epistemologica delle Matematiche nelle due culture con particolare riferimento all’argomentare e al dimostrare.
La seconda parte sperimentale
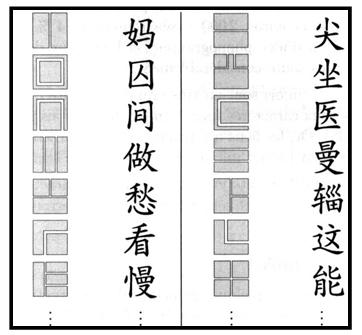
Elemento portante per tutto il lavoro di ricerca relativo alla seconda indagine sperimentale, contestualizzato attraverso una scelta metodologica quale quella della teoria delle situazioni di Brousseau (Brousseau, 1997), è stato la ferma convinzione dell’evidenza e rilevanza dell’integrazione dei saperi attraverso una possibile socializzazione degli stili cognitivi nella pratica didattica e nelle fasi di apprendimento, in particolar modo in condizioni di multiculturalità (fase di validazione della situazione a-didattica). Questo aspetto, relativo alla discussione delle contingenze sperimentali, è stato quindi l’elemento portante per la comprensione dei fenomeni di apprendimento messi in luce sul pensiero algebrico e l’integrazione dei saperi nella fase di transizione da quello aritmetico. In quest’ottica si è ritenuto necessario delineare inizialmente un breve iter storico-epistemologico capace di richiamare criticamente, in modo del tutto elementare, le fasi salienti del lungo e sofferto percorso compiuto dall’Algebra come evoluzione sull’Aritmetica e porre l’attenzione sul concetto di equazione come cuore dell’Algebra e come elemento significativo per l’indagine sperimentale. Contestualmente è stato posto l’accento sul Jiuzhang Suanshu, considerato testo rappresentativo della cultura matematica cinese antica. In esso si è cercato, seppur in una prima approssimazione di ritrovare alcune meta-regole classiche che sembrano configurarsi come fondamentali anche oggi per il pensiero algebrico e, sotto certi aspetti per la lingua cinese scritta. La figura 4 ne riporta alcune.
Fig. 4
Quest’ultimo riferimento epistemologico, trattato in un continuo bilanciamento matematica-lingua (aspetti cognitivi di codifica e decodifica della scrittura ideografica e alfabetica), è risultato centrale nella definizione delle ipotesi del lavoro di ricerca e quindi nella definizione delle variabili di comportamento controllabili sperimentalmente.La “traduzione” delle competenze matematiche connesse all’apprendimento della lingua ha evidenziato negli allievi attraverso un apprendimento parallelo di competenze matematiche/linguistiche (contestuali al processo di memorizzazione e tecniche di composizione), la “scoperta” di un primo approssimativo concetto di variabile e di equazione simbolica. Ciò che è risultato evidente è che seppur non si espliciti al ragazzo che la scrittura linguistica realizzata rappresenti un’equazione, egli in maniera implicita può acquisire delle competenze algebriche che possono rivelarsi di aiuto nel processo di interiorizzazione del pensiero algebrico formale. Questo aspetto, come sottolineato nell’articolo precedente, è in linea con quanto discusso da Needham (1981).
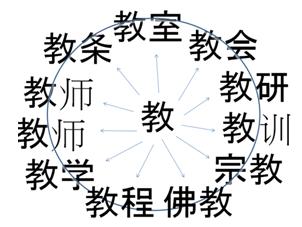
Particolarmente significativa nello studio “comparativo” è la sesta ed ultima categoria di classificazione dei caratteri cinesi (xíngshēng 形声) che si presenta come una categoria ibrida all’interno della quale l’elemento centrale che gioca un ruolo di classificazione è quello di “radicale”. La “chiave”, il radicale, secondo una lettura matematica evidenzierebbe da un lato un’incognita (un segno specifico ma “indeterminato” che assume il suo senso in relazione al contesto linguistico nel quale viene inserito); dall’altro lato però potrebbe assume il significato di segno generalizzato segno capace di veicolare il carattere nel quale esso è inserito e permettere al lettore l’identificazione di quest’ultimo. Ulteriore osservazione discussa nel lavoro in considerazione del binomio algebra-lingua cinese scritta è quella che viene fuori dall’analisi delle relazioni funzionali esistenti all’interno di un carattere composto, tra le varie parti che lo compongono. In questo senso, per quello che ci interessa specificatamente, la “chiave” assume il ruolo di parametro. Una schematizzazione di quanto detto può essere descritta attraverso l’immagine seguente che rappresenta i legami sintattici-semantici tra differenti caratteri tra loro “associati”.
Fig. 5
Volendo schematizzare i risultati ottenuti in questa seconda parte sperimentale della ricerca, sembrerebbe che gli allievi cinesi - in accordo con quanto messo in evidenza da diverse ricerche internazionali - confermino un comportamento di tipo fortemente pragmatico, concreto, messo in luce da un ragionamento di tipo algoritmico procedurale strettamente connesso al un pensiero olistico sulla codifica e decodifica delle informazioni presentate nelle varie situazioni/problema. Questi, nella fase di argomentazione e congetturazione matematica proposta sperimentalmente attraverso varie situazioni didattiche in Aritmetica e Algebra, sembrano generalmente evidenziare un approccio euristico per tentativi ed errori finalizzato, alla ricerca di un “algoritmo fondamentale” come strumento di dimostrazione. Lo stesso tipo di ragionamento aritmetico viene invece utilizzato dagli allievi italiani in una accezione non dimostrativa ma di esplorazione e congetturazione numerica che spesso limita il passaggio all’Algebra. Per gli allievi cinesi, l’argomentazione e l’organizzazione dei ragionamenti avviene generalmente per gerarchizzazione dei modelli di ragionamento che non sembrano far riferimento a logiche di tipo bivalente bensì, attraverso un uso estensivo dell’idea di “variabilità”, come relazione iniziale tra “espressioni” differenti e successivamente come “espressione” dinamica relazionata attraverso una “formula” ad altre “espressioni” anch’esse dinamiche. L’idea qui discussa può rappresentare, a nostro parere, uno degli aspetti significativi del pensiero algebrico. Il ragionamento tipico messo in luce dagli allievi italiani sembra essere invece quello di stampo aristotelico-euclideo, di tipo ipotetico-deduttivo attraverso una catena finita di congiunzioni contestualizzate ad una logica bivalente.
Schematizzando poi i differenti layers di pensiero algebrico manifestati dagli allievi cinesi ed italiani nelle varie sperimentazioni condotte (a partire dalla situazione definita per la scuola primaria a quella sul parametro contestualizzata alla scuola secondaria superiore), sembra che gli allievi cinesi, pur non evidenziando un pensiero algebrico sempre consapevole, si dimostrino maggiormente abili rispetto ai coetanei italiani come “risolutori” in contesti algebrici formalizzati e manifestino maggiore disinvoltura rispetto ai coetanei italiani nel cogliere possibili aspetti di relazione (espressi verbalmente, graficamente e sotto forma tabulare) tra variabili in gioco. Questa contingenza sperimentale sembra ritrovarsi a tutti i livelli scolastici.
In contesti non del tutto algebricamente formalizzati (denominati contesti pre-algebrici), in accordo con una loro forte tradizione storica evidenziano un ragionamento di tipo aritmetico (strettamente connesso ad una forte memorizzazione di “fatti aritmetici” che li aiutano nella definizione di un pensiero olistico di tipo relazionale) e rimangono fortemente ancorati a questo. Le argomentazioni nel processo di generalizzazione, come naturale evoluzione da un primo pensiero per prove ed errori, fa riferimento ad un pensiero di tipo algoritmico-procedurale. Le buone capacità manipolative sul simbolismo algebrico potrebbero, di contro, derivare dalla lingua scritta ideografica che, come discusso nei capitoli precedenti, sembra li aiuti fortemente nel controllo sintattico algebrico formalizzato. L’ambiente di riferimento simbolico sembra infatti, con le dovute differenze di contenuto, a loro familiare dal punto di vista procedurale.
L’idea di parametro sotteso a questo ragionamento, evidenzia un diverso comportamento delle due tipologie di allievi, forse dettato dalla peculiarità delle differenze linguistiche relative che per gli allievi cinesi, secondo le ricerche di neuroscienza discusse nei capitoli precedenti, si manifesta in un continuo bilanciamento tra un pensiero seriale, locale, ad uno globale, olistico, capace di operare categorizzazioni di tipo cognitivo e possibili generalizzazioni. Questo aspetto, analizzato qualitativamente e quantitativamente, inserito in un quadro più ampio relativo all’apprendimento del pensiero algebrico e dell’idea di variabile come “cuore” dell’Algebra, ci permette di poter ipotizzare all’interno della struttura linguistica cinese possibili strumenti di “aiuto” nel superamento di particolari ostacoli al pensiero algebrico (Spagnolo & Di Paola, 2010), elementi costruttivi della scrittura ideografica cinese che possono favorire negli anni un più facile “accesso” all’Algebra pur non garantendo agli allievi un pensiero algebrico maturo, ostacolato forse da fattori epistemologici forti, ritrovati indistintamente sia sugli allievi frequentanti le classi multiculturali palermitane che i loro coetanei non frequentanti.
Un confronto parallelo tra i comportamenti esplicitati dagli allievi cinesi ed italiani coinvolti sperimentalmente mette in luce infine una maggiore somiglianza fra i comportamenti degli allievi delle due etnie differenti là dove il grado di formalismo è più basso o addirittura nullo. Si potrebbe ipotizzare che le differenze sono più evidenti mano a mano che si sceglie l’una o l’altra modalità simbolica. Questo potrebbe dipendere dalla lingua. In accordo con l’idea secondo la quale il pensiero parallelo (messo in evidenza dagli allievi cinesi su tutti gli ordini scolastici) è essenzialmente giocato su comportamenti fuzzy dal punto di vista neuronale e che nella fase della consapevolezza del sé (Boncinelli, 1999) vi è poi un’alternanza fra pensiero parallelo e pensiero seriale, il pensiero seriale sembra corrispondere al pensiero bivalente (ritrovato generalmente tra gli allievi italiani). Questo aspetto si presenta quindi un problema aperto della nostra ricerca e necessita di ulteriori indagini sperimentali riferite ad un campione di riferimento più ampio che possa tener in considerazione non solo allievi di etnia cinese inseriti nel contesto scolastico palermitano ma anche coloro che sono inseriti nel loro contesto di studio originario.
Note
1] Tesi di dottorato di Benedetto Di Paola, relatore: Prof. Filippo Spagnolo. Dottorato di ricerca in Storia e Didattica delle Matematiche, della Fisica e della Chimica, Università di Palermo. http://math.unipa.it/~grim/Tesi_it.htm
2] Definita l’analisi a-priori dei possibili comportamenti messi in luce dagli allievi nella risoluzione della situazione sperimentale realizzata, si è provveduto, utilizzando il software di statistica inferenziale CHIC (Classification Hiérarchique Implicative et Cohesive), ad analizzare quantitativamente le contingenze esperimentali. Gli indici statistici utilizzati in questo senso sono stati l’indice di implicazione di R. Gras e l’indice di similarità di Lermann (Gras, 1979; Lermann, 1981, 2004). La definizione di variabili supplementari (Gras, Spagnolo, 2004) definite ad hoc in relazione ad alcuni aspetti epistemologici culturali per l’etnia degli allievi coinvolti, ha permesso un ulteriore approfondimento.
3] Il termine comparazione viene inteso in tutto il lavoro di tesi nell’accezione datane all’ICME-10.
4] L’insieme dei valori, modelli di comportamento, e anche delle attività materiali, che caratterizzano il modo di vita di un gruppo sociale. In una prospettiva che tenga conto dei processi comunicativi, la lingua naturale viene quindi intesa come un prodotto di una certa cultura perché ne consente la diffusione. E nello stesso tempo la cultura può essere influenzata dalla Lingua Naturale in quanto portatrice di significati storicamente rintracciati.
5] Uno degli strumenti utilizzati nella storia della Matematica cinese per dimostrare la conformità di una sequenza di passaggi rispetto ad una classe di problemi concreti, è l’algoritmo. L’algoritmo è inteso come iterazione di due scelte condizionali (se..allora) con un punto di partenza qualsiasi.
Bibliografia
Ajello M., Spagnolo F., Z. Xiaogui. (2005), Reasoning Patterns and logical-linguistic Questions in European and Chinese Cultures: Cultural Differences in scholastic and non-scholastic Environments, Mediterranean Journal for Mathematics Education, Cyprus Mathematical Society (ISSN 1450-1104), Vol. 4, N. 2, pp. 27-65.
Arzarello F., Bazzini L. & Chiappini G. (1994), L’Algebra come strumento di pensiero. Analisi teorica e considerazioni didattiche. Progetto Strategico del C.N.R. Pavia: Dipartimento di Matematica: Università di Pavia, Quaderno n. 6.
Bartolini Bussi M. G. (2008), Perché i bambini cinesi sono più bravi in matematica? Alla ricerca di una risposta nei loro libri di testo di prima e seconda elementare, in Conferenze e Seminari dell'Associazione Subalpina Mathesis 2007-2008, Torino: Kim Williams Books.
Boncinelli E. (1999), Il cervello, la mente e l’anima, Mondadori, Milano
Brousseau G. (1997), Theory of didactical situations in mathematics. Edited and translated by Balacheff, Kluwer academic publishers.
Cai J. & Nie B. (2007), Problem solving in Chinese mathematics education: research and practice, ZDM the International Journal on Mathematics Education, 39, pp. 459-473.
Chemla K. (2001), I “Nove capitoli sui procedimenti matematici”: la costituzione di un canone nella matematica, Storia della Scienza: Cina, India, Americhe, Istituto della Enciclopedia Italiana fondata da Giovanni Treccani S.p.a., pp. 133-153.
Chemla K. & Shuchun Guo. (2004), Les Neuf Chapitres, Ed. Dunod, Paris.
Shen Kangshen, John N.Crossley & Antony W.-C. Lun. (1999) The Nine Chapters on the Mathematical Art, Oxford University Press, Science Press – Beijing.
D’Ambrosio U. (2002), Etnomatematica. Bologna: Pitagora Editrice
Di Paola B., Spagnolo F. (2009), Argumentation and Proving in Multicultural Classes: A didactical experience with Chinese and Italian students, Journal of Mathematics Education, December 2009, Vol. 2, No. 1, pp.1-14. Annually in hard copy (ISSN 1945-7502) and online (ISSN 1945-7 448).
Di Paola B., Spagnolo F. (2009), Indeterminate systems in the “Nine Chapters” by Liu Hui. The role of “context” for determining the “fundamental algorithm” as an argumentative tool. The 3rd International Symposium on the History and Pedagogy of Mathematics in China, Beijing Normal University.
Di Paola B. (2009), Pensiero aritmetico e pensiero algebrico in ambienti multiculturali: il caso cinese, tesi di dottorato pubblicata in rete all’indirizzo web http://math.unipa.it/~grim/
Di Paola B., Spagnolo F. (2010), European and Chinese Cognitive Styles and their impact on Teaching/Learning Mathematics, Journal of Mathematics Education, December 2010, Vol. 3, No. 2, pp.139-153. Annually in hard copy (ISSN 1945-7502) and online (ISSN 1945-7 448).
Gras R., Spagnolo F. (2004), Fuzzy implication through statistic implication: a new approach in Zadeh’s framework, 23rd International Conference of the North American Fuzzy Information Processing Society, NAFIPS (IEEE), Banff, Canada, Edited by Scott Dick-Lukasz Kurgan-Petr Musilek-Witold Pedrycz-Mark Reformat (IEEE Catalog 04TH8736, ISBN 0-7803-8376-1), pp. 425-429, Vol I.
Kosko B. (1995), Il Fuzzy Pensiero, Baldini&Castoldi, Milano. (Fuzzy thinking: the new Science of fuzzy logic, B. Kosko, 1993).
Leung, F.K.S., Graf, K.-D., Lopez-Real, F.J. (Eds.), (2006). Mathematics Education in Different Cultural Traditions: A Comparative Study of East Asia and the West, Springer.
Malisani E. (2005). The notion of variable: some meaningful aspects of algebraic language. In A. Gagatsis, F. Spagnolo, Gr. Makrides & V. Farmaki (eds.), Proceedings of the 4th Mediterranean Conference on Mathematics Education (MEDCONF 2005), University of Palermo, Italia. Vol. II, pp. 397-406.
Malisani, E. & Spagnolo, F. (2005). Difficulty and obstacles with the concept of variable. Proceedings CIEAEM 57, pp. 226-231. Piazza Armerina, Italia.
Needham J. (1981), Scienza e Civiltà in Cina. (Original title: Science and Civilisation in China, Cambrige University Press, 1959), I e II Vol., Einaudi.
Nisbett R.E (2003), The Geography of Thought, Nicholas Brealey Pbl. ltd., London.
Nisbett R.E., Peng K., Choi I., Norenzayan A. (2001), Culture and Systems of Thought, Psychological Review, 108, p. 291.
Spagnolo F. (2005), Reasoning Patterns and logical-linguistic Questions in European and Chinese Cultures: Cultural Differences in scholastic and non scholastic Environments, The International Conference on School effectiveness and School improvement in China, University of Shenyang, China, (p. 76).
Spagnolo F. (2002), History and Ethno-Mathematics in the Interpretation of the Process of Learning/Teaching, 13° ICME Comparative Study Conference, University of Hong Kong.
Spagnolo F. (1986), Sull’impostazione di certi metodi risolutivi dei problemi nella tradizione cinese, L’insegnamento della Matematica, vol. 9, n. 8, pp. 81-91.
Spagnolo F. (2003), Fuzzy logic, Fuzzy Thinking and the Teaching/Learning of Mathematics in multicultural Situations, General conference, Brno (Ceck Republic), International Conference on Mathematics Education into the 21st Century, pp. 17-28.
Spagnolo F., Di Paola B. (2010), European and Chinese Cognitive Styles and their impact on Teaching Mathematics, Springer, Studies in Computational Intelligence, ISBN 978-3-642-11679-7; ISSN 1860-949X.
Sun Miantao (2005), The Concept of Tizhi (system) in Chinese Education, Liaoning Peoples Publishing House, China (ISBN 7-205-05844-9).