La macchina che gioca a NIM
"Gli uomini non sono mai così ingegnosi come quando inventano i giochi: la mente trova grande soddisfazione in quest'attività... dopo quelli che dipendono esclusivamente dai numeri ci sono quelli di posizione, [dopo ancora] vengono quelli che coinvolgono il movimento... Alla fine possiamo sperare che arriveranno anche quelli matematici."
Gottfried Leibniz (1646-1716)
In Internet si trovano facilmente programmi che permettono di giocare a NIM, in tali giochi si parte da un numero fisso (non modificabile) di monete o fiammiferi o con un valore random limitato. Scopo dell'articolo è mostrare come sia possibile costruire una macchina (programmata in Java) che giochi a NIM e vinca sempre e lasciando scegliere al giocatore il numero di monete da usare per la partita.
Una definizione classica lo presenta come 'un'attività gestuale o intellettuale che ha come unica finalità quella di divertire la persona che vi si dedica'. Il gioco matematico copre un campo molto vasto dai puzzle agli enigmi. I giochi possono essere sostanzialmente classificati secondo il seguente schema:
- giochi di pura fortuna o d'azzardo (tipo lotto o roulette);
- giochi di pura abilità (scacchi, esapedone, NIM);
- giochi misti di abilità e fortuna (gran parte dei giochi di carte, monopoli, risiko, Master Mind).
Figura 1
Il NIM (fig. 1.a e 1.b )è considerato uno dei più antichi giochi matematici, probabilmente di origine cinese. Deve il suo nome al matematico americano Charles Leonard Bouton, professore incaricato all'Universtità di Harvard, presumibilmente in riferimento all'arcaico verbo inglese che significa portar via o rubare. E' conosciuto anche con il nome di gioco di Marienbad, con riferimento a un film del 1961 in cui si vedono due personaggi alle prese con un simile gioco. Di solito lo si fa con dei fiammiferi, ma va bene qualsiasi oggetto (purché ...in numero sufficiente). Si dispongono questi oggetti in piccoli mucchi o pacchetti e i due giocatori, a turno, tolgono tanti oggetti quanti ne vogliono ma da un solo mucchio (almeno un oggetto e , al massimo, tutto il mucchio). Il giocatore che non riesce più a giocare perde; quello che ha fatto l'ultima mossa vince. Nella versione più popolare del gioco vi erano 12 oggetti distribuiti su tre mucchi (3 ogg., 4 ogg., 5 ogg.).
Il gioco è classificato tra quelli di pura abilità in quanto è possibile stabilire una strategia vincente che permetterebbe al primo o al secondo (dipende dalla distribuzione degli oggetti) che fa la mossa di vincere sempre anche se l'avversario giocasse al meglio delle sue possibilità. Bouton fu il primo a pubblicare un'analisi completa del gioco e spiegare la strategia per un qualsiasi numero di oggetti. Ogni combinazione di oggetti è o 'sicura' o 'pericolosa' . Se la situazione lasciata dal primo giocatore è 'sicura' allora questi è il candidato a vincere la sfida, qualsiasi sia la mossa dell'avversario, viceversa se la situazione dopo la mossa è 'pericolosa' il candidato a vincere (se conosce la strategia ) è il secondo giocatore. Per giocare secondo la strategia ciascun giocatore deve muovere con l'obiettivo di disporsi in un situazione 'sicura'. Una situazione si dice 'sicura' quando la somma dei numeri relativi ai mucchi e rappresentati mediante la notazione binaria, somma effettuata senza riporto, dà come risultato 0 e si dice 'pericolosa' in caso contrario.
Ecco un esempio di situazione 'pericolosa' e di una 'sicura':
3 1 1 1 1
4 1 0 0 4 1 0 0
5 1 0 1 5 1 0 1
--------- ------------
0 1 0 0 0 0
Per passare da una situazione 'pericolosa' ad una 'sicura' basta togliere qualche oggetto da uno dei mucchi in modo tale da ottenere tutti zeri mentre ogni volta che bisogna muovere a partire da una situazione 'sicura' si passa inevitabilmente in una situazione 'pericolosa'. Molte persone si sono dedicate alla costruzione di macchine che potessero giocare a Nim e fossero in grado di vincere. La macchina Nimatron viene brevettata nel 1940, intorno agli anni '50 ne è stata brevettata una (Nimrod) e presentata alla fiera commerciale di Berlino. Nimrod divenne popolare per aver sconfitto il ministro dell'economia , Dr. Erhard, in tre partite.
In rete si trovano diversi giochi di NIM con grafica accattivante, tali giochi hanno numero degli oggetti per mucchio fissi o comunque limitati ad un numero piccolo. La mia idea è stata quella di proporre all'utente una partita in cui sia lui a stabilire il numero dei mucchi e il numero di oggetti per mucchio. Ho quindi elaborato un algoritmo che consenta al computer di vincere in ogni caso, ho trascurato l'aspetto grafico che si può comunque dedurre facilmente dai vari programmi in rete . Il programma è così strutturato:
import java.io.*;
public class nim {
public static void main(String[] args) throws IOException {
int n, i, vettore[], a1, vett2[], a3;
String input, a2, vett1[];
boolean a5 = false;
a3=0;
InputStreamReader flusso = new InputStreamReader(System.in);
BufferedReader tastiera = new BufferedReader(flusso);
System.out.println("Inserisci il numero di righe");
input = tastiera.readLine();
n = Integer.parseInt(input);
vettore = new int [n];
vett2 = new int [n];
vett1 = new String [n];
for(i=0;i<n;i++){
a1 = i+1;
System.out.println("Inserisci il numero di monete per la "+ a1 +"-ma riga");
input = tastiera.readLine();
vettore[i] = Integer.parseInt(input);
vett1[i] = Integer.toBinaryString(vettore[i]);
vett2[i] = vett1[i].length();
}
a3 = max(vett2,n);
a5 = controllo(vett2,vett1,n,a3);
boolean fine = false;
if (a5 == false)
{System.out.println("Comincio io");
while (fine == false){
a3 = max(vett2,n);
miamossa(a5, vettore, vett1, vett2, a3, n);
fine=controlfine(vettore,n);
if (fine == false) {
tuamossa(vettore, vett1, vett2, n);
a5 = controllo(vett2, vett1, n, a3);
fine = controlfine(vettore,n);}}
}
else
{System.out.println("Comincia tu");
while (fine == false){tuamossa(vettore, vett1, vett2, n);
fine = controlfine(vettore,n);
if (fine == false) {
a5 = controllo(vett2, vett1, n, a3);
miamossa(a5, vettore, vett1, vett2, a3, n);
fine = controlfine(vettore, n);}
}
}
System.out.println("Ho vinto io, riprova sarai più fortunato");
}
public static int max( int vett2[], int n)
{ int a4 = vett2[0];
for (int i=0;i<n;i++){
if (vett2[i]>a4) {a4 = vett2[i];};}
return a4;
}
public static boolean controllo( int vett2[], String vett1[], int n, int a3)
{
boolean a6 = true;
int l=0;
while (l<a3 & a6 == true){
if (a6 == true) {
int cont=0;
for (int j=0; j<n;j++){
int a4=vett2[j]-1-l;
if (a4>=0) {if (vett1[j].charAt(a4)=='1') cont=cont+1;
}}
if (cont%2 == 1){ a6 = false;}}
l=l+1; }
return a6;
}
public static void tuamossa (int vettore[], String vett1[], int vett2[], int n)throws IOException
{ String input1;
InputStreamReader flusso = new InputStreamReader(System.in);
BufferedReader tastiera = new BufferedReader(flusso);
System.out.println("Inserisci il numero di riga che vuoi modificare");
input1=tastiera.readLine();
int a7=Integer.parseInt(input1)-1;
System.out.println("Inserisci il numero di monete per la "+ input1 +"-ma riga");
input1=tastiera.readLine();
vettore[a7]=Integer.parseInt(input1);
vett1[a7]=Integer.toBinaryString(vettore[a7]);
vett2[a7]=vett1[a7].length();
System.out.println("Mossa tua");
for(int i=0;i<n;i++){
System.out.println(vettore[i]);
}
}
public static void miamossa(boolean a5,int vettore[], String vett1[], int vett2[], int a3,int n)
{int k=0;
while (a5==false & k<n){
int a8=vettore[k];
String a9=vett1[k];
int a10=vett2[k];
int a11=a3;
while (a5==false & vettore[k]>0){
vettore[k]=vettore[k]-1;
vett1[k]=Integer.toBinaryString(vettore[k]);
vett2[k]=vett1[k].length();
a3=max(vett2,n);
a5= controllo(vett2,vett1,n,a3);}
if (a5==false) {vettore[k]=a8;
vett1[k]=a9;
vett2[k]=a10;
a3=a11;
k=k+1;
}}
System.out.println("Mossa mia");
for(int i=0;i<n;i++){
System.out.println(vettore[i]);
}}
public static boolean controlfine( int vettore[], int n)
{boolean fine1=true;
for(int i=0;i<n;i++) if (vettore[i]!=0) {fine1=false;}return fine1;}
}
Nella parte principale (main) si inserisce in Input il numero (n) di mucchi (righe) successivamente, con un ciclo for si inseriscono i numeri di oggetti (vettore[i]) per mucchio, si convertono i numeri da notazione decimale a binaria e si registra la lunghezza del numero così ottenuto, si prende a riferimento la stringa di numeri più lunga (a3) e con la procedura di controllo si procede a verificare se la condizione di partenza è 'sicura' o 'pericolosa', si applica un controllo 'verticale' dei numeri espressi in forma binaria (cioè controllo tutte le a4-me cifre dei numeri in binario, se vett1[j].charAt(a4) vale '1' incremento il contatore). Se il computer scopre di essere in una posizione 'sicura' allora fa muovere l'utente, se si trova in una posizione 'pericolosa' muove per primo. Con la procedura miamossa il computer deicide la mossa: la mossa consiste nel togliere un oggetto per volta da un mucchio e controllare se vi sia un situazione 'sicura', in caso contrario si rimette tutto a posto. Con la procedura tuamossa l'utente fa la sua mossa ed il computer si limita a registrare i dati. La procedura controlfine permette di verificare se la configurazione finale risulta di tutti zeri. Si potrebbe far notare agli studenti che il programma così strutturato è piuttosto complesso e invitare alla compilazione di uno più 'economico'.
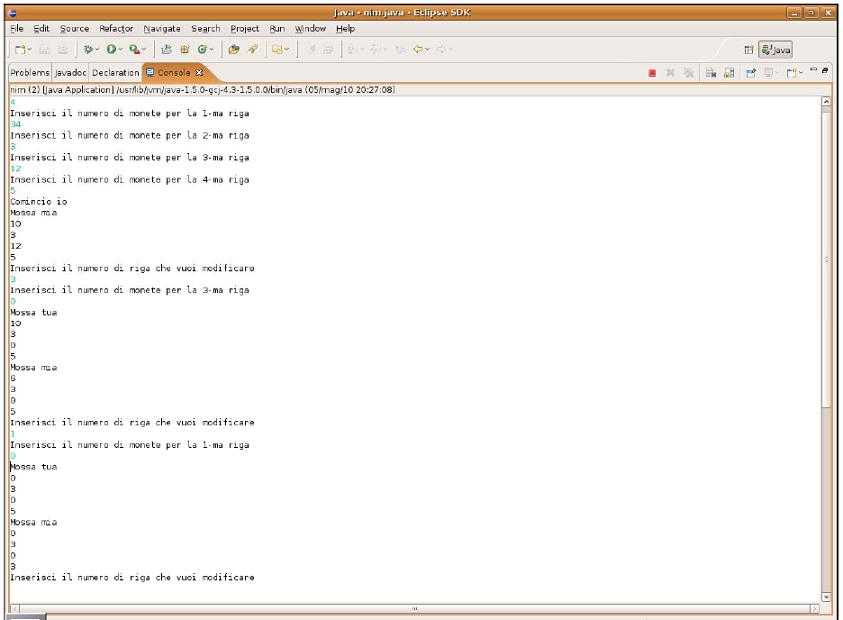
Si propone di far giocare prima gli studenti tra loro varie partite di NIM allo scopo di prendere confidenza con lo stesso (magari organizzare un campionato). Farli giocare contro il computer con le varie versioni che ci sono in Internet. Successivamente spiegare la strategia vincente e proporre di costruire insieme la macchina imbattibile. Di seguito in figura viene mostrata un segmento di partita.
Bibliografia
Martin Gardner, Enigmi e giochi matematici, vol. 1, Ed. Sansoni, 1990, pp.130-139.
I giochi matematici, Lettera Matematica Pristem, n.54, febbraio 2005.
Claudio Bernardi, Appunti di matematiche complementari I, 1988.