La Probabilità nella vita quotidiana - Introduzione elementare ai modelli probabilistici

Probabilità: un concetto intuitivo

A ben pensarci, la nostra vita di tutti i giorni è costellata da considerazioni di natura probabilistica, anche se non necessariamente formalizzate come tali. Sono esempi di ciò la valutazione, nell’uscire di casa la mattina, della possibilità che piova o meno nel corso della giornata (per decidere se prendere o no l’ombrello), la rinuncia a partecipare ad una gara o un concorso “perché non ho possibilità di farcela”, le previsioni del tipo “la squadra X ha ormai vinto al 90% il campionato”, le statistiche che ci informano sulle probabilità di morte per il fumo o per il mancato uso delle cinture di sicurezza in caso di incidente stradale, per non parlare delle speranze di vincita in giochi e lotterie.
In tutte le situazioni di incertezza, si tende in sostanza a dare una “misura” dell’incertezza che, sia pur indicata con vari termini, esprime il significato intuitivo della “probabilità”. Il fatto che la probabilità abbia un significato intuitivo comporta anche che lo stabilirne le regole può, entro certi limiti, essere guidato dall’intuizione. Tuttavia l’affidarsi completamente all’intuizione può portare a conclusioni scorrette.
Vediamone alcuni esempi.
Nel suo numero del 1 Novembre 1989, il quotidiano americano The Star-Democrat riportava la seguente affermazione, tragica trasposizione alla vita reale della barzelletta di quel tale che pretende di viaggiare in aereo portandosi una bomba perché è nulla la probabilità di 2 bombe sullo stesso aereo: “secondo il padre, il pilota (morto mentre cercava di atterrare sulla nave USS Lexington) era certo che non sarebbe mai stato coinvolto in un incidente aereo perché il suo compagno di stanza era morto in uno di questi e la probabilità era contraria”.

 Nel bollettino mensile di una nota carta di credito, nel numero di settembre 2002 si poteva leggere: “da sempre [il circuito mondiale di sportelli Bancomat] offre un servizio ai massimi livelli in termini di qualità, con una percentuale di transazioni con esito positivo pari al 99%”. La percentuale di successi vantata non è poi così favorevole se si pensa che, usando la carta per un anno una volta alla settimana la probabilità che almeno una transazione abbia esito negativo è pari a circa il 41%.
La pubblicità su quotidiani e riviste riporta spesso mirabolanti promesse di vincita come la seguente, apparsa su un noto quotidiano il 10 gennaio 2003: “sulla ruota di Roma, dal 1945 ad oggi, non si era mai fatto attendere per più di 82 estrazioni consecutive: il numero attualmente in maggiore ritardo potrebbe ritornare da un momento all’altro. Il 73 di Roma è meglio attaccarlo affidandosi alla vera statistica piuttosto che a maghi e veggenti. ... Dopo l’estrazione di mercoledì scorso [l’autore del metodo] ha trovato i migliori numeri da abbinare al 73 di Roma e messo a punto una appropriata strategia per le ultime prossime estrazioni. ... (1.50 Euro + IVA al minuto, max. 8 minuti)”.
Non è poi così difficile rendersi conto che, se il gioco non è truccato (come dobbiamo credere fino a prova contraria), cioè se – ad ogni estrazione – ogni numero ha la stessa possibilità di essere estratto e il meccanismo di estrazione non è influenzato da quanto avvenuto nelle estrazioni precedenti, allora il fatto che un numero sia ritardatario non ne aumenta la probabilità di essere estratto. Per gli increduli (o creduloni?), torneremo sulla questione nel seguito.
Per evitare di pervenire a conclusioni scorrette, è necessario formalizzare il Calcolo delle probabilità stabilendone le regole e i concetti in modo logico e rigoroso ed è qui che la Matematica entra in gioco.

Breve storia del Calcolo delle probabilità

 Le origini del (moderno) Calcolo delle probabilità si fanno tradizionalmente risalire alla corrispondenza tra Pascal e Fermat su un problema di gioco d’azzardo (1654): un noto giocatore dell’epoca riscontrava che le sue deduzioni probabilistiche non si accordavano con le sue fortune, o meglio sfortune, di gioco e si rivolse a Pascal chiedendo lumi al riguardo. Nato come teoria matematica dei giochi, il Calcolo delle probabilità crebbe progressivamente di importanza tanto che già Laplace, agli inizi del XIX secolo ([1], p. 123), poteva affermare “è notevole il fatto che una scienza, iniziata con l’analisi dei giochi d’azzardo dovesse essere elevata al rango dei più importanti oggetti della conoscenza umana”. La teoria conobbe un grande sviluppo nel XX secolo, quando Kolmogorov nel 1933 [2] introdusse l’approccio assiomatico che ancora oggi ne costituisce il fondamento.
Al giorno d’oggi, le applicazioni del Calcolo delle probabilità sono presenti in ogni ramo della scienza, nella tecnologia, nella finanza. Del resto, la fine della visione newtoniana della Fisica e l’avvento di quella quantistica hanno dimostrato l’impossibilità di fare previsioni esatte in ogni circostanza: il principio di indeterminazione di Heisenberg (1927) afferma che non è possibile conoscere simultaneamente la posizione e la velocità di un dato oggetto con precisione arbitraria.
Nel secolo XX ebbe anche grande impulso la Statistica, che del Calcolo delle Probabilità rappresenta in un certo senso il “braccio operativo”, studiando come combinare le probabilità che misurano l’incertezza relativa ad un certo fenomeno con le osservazioni sperimentali del fenomeno stesso.

La costruzione di un modello probabilistico: gli ingredienti essenziali
 

Possiamo definire il Calcolo delle probabilità come la teoria matematica dell’incertezza. La teoria dice come si devono formulare in maniera corretta delle valutazioni probabilistiche o, in altri termini, come si deve formulare un modello probabilistico. Come ogni modello matematico, anche quello probabilistico, da un lato, consente la trattazione di un problema di interesse in modo logico e rigoroso; dall’altro, rappresenta necessariamente un’astrazione della realtà e ne cattura solo alcuni aspetti. Inoltre, il modello deve condurre a risultati “utili”, che siano in accordo con l’evidenza sperimentale. Altrimenti se ne impone la revisione.
Un aspetto affascinante del Calcolo delle probabilità è la possibilità di affrontare problemi interessanti e che bene ne illustrano le potenzialità con modelli semplici e con una Matematica sostanzialmente elementare. Questo non vuole dire che il Calcolo delle probabilità è una disciplina facile. Esistono molti problemi interessanti che richiedono modelli più complessi e strumenti matematici sofisticati, come è il caso dei fenomeni aleatori che evolvono nel tempo, per i quali occorre definire appropriati processi stocastici. I modelli più complessi pongono anche problemi non banali dal punto di vista computazionale.
Vediamo ora quali sono gli elementi essenziali per la costruzione di un modello probabilistico.
Occorre innanzitutto individuare quali sono gli eventi in gioco, cioè le diverse situazioni che si possono presentare quando si considera un certo fenomeno, in particolare gli eventi elementari o esiti. Per illustrare questi concetti, peraltro piuttosto intuitivi, ricorriamo ad un semplice esempio.
Consideriamo il lancio simultaneo di due dadi di diverso colore: gli esiti, o eventi elementari, possono essere individuati dalle coppie ordinate di interi da 1 a 6. A partire dagli eventi elementari si possono costruire eventi “complessi”, quali l’evento “uscita di un 7 (come somma)”, che possiamo descrivere come la collezione di esiti:

E={(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)} .

L’insieme dei possibili esiti, nel nostro esempio le 36 coppie ordinate di interi da 1 a 6, è detto spazio campionario (S).
È evidente che possiamo descrivere gli “oggetti” sopra introdotti in termini insiemistici: lo spazio campionario può essere visto come un insieme del quale gli esiti costituiscono gli elementi o “punti”. Gli eventi sono allora sottoinsiemi dell’insieme S.
Come abbiamo già ricordato, il modello probabilistico è una astrazione della realtà che ne cattura alcuni aspetti. Non sorprenderà quindi l’osservazione che lo spazio campionario è una costruzione matematica non necessariamente unica, che dipende da ciò che pensiamo sia importante.
Se il lancio dei due dadi del nostro esempio avviene sul pavimento del salotto, i dadi possono finire sotto il divano che ne nasconderà il valore della faccia superiore. Se si è interessati a tenere conto di questo fatto, si potrà “arricchire” lo spazio campionario con la coppie (D,i), (i,D), i=1,…,6, (D,D).

Analoghe considerazioni possono essere fatte per gli eventi: una volta fissato lo spazio campionario, quali considerare dipende da cosa si ritiene importante. Se l’interesse è per l’evento E “uscita di un 7”, sarà sufficiente limitarsi a considerare l’evento E e l’evento complementare E segnato.

Se si deve decidere se fare o meno una gita per il giorno successivo e quale abbigliamento prevedere in caso di effettuazione tenendo conto delle previsioni di pioggia, gli eventi da considerare potrebbero essere “tempo asciutto”, “pioggia leggera”, “pioggia intensa” e non necessariamente i millimetri di pioggia che potrebbero cadere sul luogo della gita.
Quando gli esiti possono essere contati, lo spazio campionario si dice discreto. Come caso particolare, se il numero di esiti è limitato, lo spazio campionario si dice finito.
Dopo avere introdotto gli eventi, vediamo ora come assegnare ad essi le probabilità, per essere in grado di misurare –questo appunto è lo scopo del Calcolo delle probabilità– l’incertezza relativa al verificarsi o meno di un evento.
Quando lo spazio campionario S è discreto, è facile costruire la probabilità di un evento a partire dalle probabilità degli eventi elementari. È del tutto naturale pensare a queste ultime come dei numeri reali compresi tra 0 e 1, così che, ad esempio, un esito al quale sia assegnata la probabilità 0, 2 è ritenuto 2 volte più probabile di uno con probabilità 0, 1. Un evento certo riceverà probabilità 1 e un evento impossibile probabilità 0. Pure naturale è l’assegnazione, di conseguenza, di una probabilità ad ogni evento E: essendo questo una collezione di esiti ei1,…,eik, …, sarà immediato assegnare a E la somma delle probabilità degli esiti, così che P(E)=Σkpik, dove pik=P(eik) e la somma deve intendersi come una serie se gli esiti sono un’infinità numerabile. Per il fatto che la collezioni di tutti gli esiti costituisce lo spazio campionario S, che può quindi essere considerato come un evento certo, sarà Σk pk=P(S)=1. Se E non contiene esiti si conviene che P(E)=0. Immediata conseguenza della definizione di probabilità di un evento sopra introdotta è che, se A e B sono due eventi, allora P(A∪B)=P(A)+P(B)-P(AB), dove AB indica l’evento costituito dal verificarsi contemporaneo di A e di B, cioè A∩B nella consueta notazione insiemistica. In particolare, se A e B sono disgiunti (o “incompatibili”), risulta P(A∪B)=P(A)+P(B), così che P(A segnato)=1-P(A).
Una assegnazione delle probabilità {pi, i=1,2,…} degli esiti {ei, i=1,2,…} viene detta distribuzione di probabilità su S.
Il problema naturalmente è come assegnare, nel concreto, i valori numerici di una distribuzione di probabilità.
Nel nostro esempio del lancio dei due dadi (senza divano…), è naturale pensare che nessun esito ei sia “favorito”, almeno se non abbiamo motivo di ritenere che i dadi siano truccati, e di conseguenza assegnare a tutti gli esiti la stessa probabilità. Così facendo, la condizione Σipi=P(E)=1 fornisce immediatamente P(ei)=1/36 per ogni i.
Questa distribuzione di probabilità è un esempio di distribuzione uniforme discreta. Naturalmente tale distribuzione può sussistere solo quando lo spazio S è finito.

Le definizioni di probabilità e l’impostazione assiomatica

La questione della individuazione di una appropriata distribuzione di probabilità è strettamente connessa con il problema della definizione stessa di probabilità come misura dell’incertezza. Esistono sostanzialmente tre definizioni di probabilità:

• definizione soggettiva della probabilità ([3], de Finetti): la probabilità è il prezzo che un individuo “coerente” ritiene equo pagare per ricevere 1 se l’evento si verifica e 0 altrimenti; in sostanza, è questa la definizione che abbiamo utilizzato per assegnare la distribuzione uniforme discreta agli esiti del lancio dei due dadi, sia pure in modo mascherato invocando la considerazione che nessun esito possa considerarsi favorito;
  
  
• definizione classica di probabilità: la probabilità è vista come il rapporto tra il numero di casi favorevoli ad un certo evento e il numero di casi possibili, purchè questi ultimi abbiano la stessa possibilità di verificarsi. Questa definizione, di cui risalta immediatamente il carattere tautologico, risente delle circostanze in cui è nato il Calcolo delle probabilità (in relazione a problemi di gioco d’azzardo) e può essere fatta risalire a Pascal; in realtà, è piuttosto una regola per calcolare le probabilità in situazioni in cui ci sia un numero finito di alternative che possono essere considerate, per motivi di simmetria e simili, ugualmente probabili;
  
  
• definizione frequentista di probabilità: può essere empiricamente riscontrato che, se si osservano gli esiti di successive repliche di un esperimento, la frequenza relativa di un evento associato a tali esiti (ad esempio l’uscita di una testa nel lancio di una moneta o, nel lancio di due dadi, l’uscita di un doppio sei), tenderà a stabilizzarsi su un certo valore che sarà pari a 1/2 nel lancio della moneta e a 1/36 nel lancio dei due dadi. La coincidenza di tale valore con il valore calcolato secondo la definizione classica di probabilità ha portato a definire la probabilità di un evento come il limite della frequenza relativa del verificarsi dell’evento quando il numero delle prove tende all’infinito. Anche questa definizione non è esente da critiche, legate in sostanza al problema di definire cosa si intenda per limite e alla possibilità di ripetere all’infinito un esperimento nelle stesse condizioni.
  

Tutte e tre queste definizioni conducono in realtà alle stesse regole-base del calcolo delle probabilità:

1) P(A)≥0, " evento A;
2) se A è l’evento certo, allora P(A)=1;
3) se A e B sono eventi incompatibili, P(A∪B)=P(A)+P(B).

Pertanto, al di là delle diverse interpretazioni della probabilità, è possibile costruire una teoria che dica come costruire modelli probabilistici e analizzarne le implicazioni in modo rigoroso. È quanto ha realizzato la impostazione assiomatica di Kolmogorov (1933), che ha definito come assiomi una riformulazione delle regole 1), 2), 3), valida per spazi di natura qualsiasi nei quali sia individuata una collezione di sottoinsiemi –chiamata σ-algebra– comprendente lo spazio stesso e chiusa rispetto all’unione numerabile e al complementare. Una delle diverse formulazioni equivalenti degli assiomi di Kolmogorov è la seguente:

Sia Ω uno spazio e F una σ-algebra non vuota di suoi sottoinsiemi; questi ultimi sono detti eventi. Una probabilità P è una funzione a valori reali definita sugli eventi e tale che:

1. P(A)≥0, " ∀ A∈F;
2. P(Ω)=1;
    

se A1, A2,… è una successione al più numerabile di eventi a due a due incompatibili, P(∪iAi)=Σi P(Ai).

È naturale chiedersi se l’impostazione assiomatica, oltre a permettere lo sviluppo di un rigoroso calcolo delle probabilità, sia anche “utile”, nel senso di permettere la costruzione di modelli in accordo con l’evidenza sperimentale. La risposta a tale domanda è positiva, come dimostra tra l’altro il fatto che è possibile dare una formulazione rigorosa di quella legge empirica del caso suggerita dall’evidenza sperimentale, nel caso di prove ripetute in modo indipendente e nelle stesse condizioni e che è alla base della definizione frequentista di probabilità.

Le insidie del Calcolo delle probabilità

La possibilità di poter disporre di un apparato matematico per il calcolo delle probabilità permette di superarne le insidie, che sono di varia natura, ma sono in buona parte legate a una eccessiva confidenza nelle capacità dell’intuizione. Ne esaminiamo alcune che appaiono come le principali fonti di errore nella valutazione della probabilità di eventi di interesse.

Il conteggio dei casi
Una prima fonte di errore è, nel caso di spazi finiti, il conteggio dei casi. Nell’esempio del lancio dei due dadi, confondere i due eventi uscita di (1,6) e uscita di un 1 e di un 6 porterebbe a conclusioni scorrette in quanto:

1/36=P(uscita di (1,6))≠P(uscita di un 1 e di un 6)= P(uscita di (1,6))+ P(uscita di (6,1))=1/18.

Spesso i principianti sono messi in difficoltà di fronte alla richiesta di calcolare la probabilità di eventi del tipo almeno, che è invece facilmente ottenibile considerando l’evento complementare. Ad esempio, dalla identità
P(E segnato)=1-P(E), si ottiene immediatamente:

P(almeno una faccia > 2 )
=1 - P(tutte e due le facce ≤ 2 )
=1 - P((1,1)∪(1,2)∪(2,1)) = 1 – 3/36.

Per spazi campionari finiti, il calcolo delle probabilità richiede tipicamente l’utilizzo di formule del calcolo combinatorio, come il coefficiente binomiale: 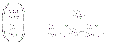che esprime il numero di gruppi di k oggetti diversi presi tra n. Anche in questo caso, la mancata conoscenza di identità del tipo:
o di formule di approssimazione come quella di Stirling n!=nⁿe^-n√(2πn) può mettere in serie difficoltà chi si avventuri privo del necessario equipaggiamento nel mondo della probabilità.

L’abuso dell’equiprobabilità

Un’altra insidia è costituita dalla acritica supposizione dell’equiprobabilità delle diverse alternative. Non è poi così difficile lanciare in aria con la mano una moneta in modo che ricada nel palmo con la stessa faccia iniziale! Nel qual caso, supporre che le due facce della moneta siano equiprobabili porterebbe l’ingenuo scommettitore a sperimentare delle amare sorprese.

Non è tuttavia necessario pensare ad imbrogli da parte del lanciatore. Esistono diverse esperienze che dimostrano come la rotazione di una moneta su una superficie liscia, invece del suo lancio, possa portare a significative differenze nella frequenza delle facce legate alla posizione del centro di massa della moneta determinata dalle inevitabili diversità delle due facce. Uscendo dal campo dei giochi, l’ipotesi che la distribuzione di probabilità del picco orario di chiamate ad un call center sia uniforme sulle 24 ore può essere certamente semplificatrice dal punto di vista del calcolo, ma ne appare evidente il limite (a meno che non si stia considerando un call center operante su scala mondiale).
Occorre ricordare che un modello probabilistico, come ogni modello, costituisce comunque una approssimazione della realtà; ipotesi semplificatrici possono essere opportune per un primo approccio ad una situazione complessa. Spesso la semplificazione permette di ottenere risposte comunque utili, che un modello più complesso non riuscirebbe a fornire per le difficoltà, analitiche o computazionali, che insorgerebbero nel trattarlo. È tuttavia importante che le ipotesi sulle quali il modello si basa vengano apertamente dichiarate per mettere in guardia su possibili limiti delle conclusioni a cui l’analisi del modello ha portato, in vista di eventuali raffinamenti successivi.

Eventi rari possono accadere

Un errore in cui incorre spesso il senso comune è quello di equiparare eventi rari, cioè eventi a cui è associata una probabilità piccola di verificarsi, ad eventi impossibili. Il fatto che una determinata persona vinca ad una lotteria nazionale è sicuramente un evento raro, ma se la sua vincita venisse considerata impossibile si dovrebbe considerare impossibile la vincita da parte di chiunque altro (perché l’estrazione dovrebbe fare preferenze?) e di conseguenza si dovrebbe ritenere impossibile che ci sia un vincitore della lotteria, il che è assurdo.
Possiamo ricorrere ad un modello molto usato in situazioni di questo genere per rendere più precise le nostre considerazioni: lo schema di Bernoulli. Questo modello si applica a situazioni in cui si possa svolgere una successione infinita di esperimenti indipendenti e nelle stesse condizioni con esito successo (cioè un certo evento, non necessariamente fausto, si verifica) o insuccesso (l’evento non si verifica).

Sia p la probabilità di successo in ciascun esperimento e T il tempo di primo successo, cioè il numero d’ordine dell’esperimento in cui per la prima volta si verifica un successo dopo una sequenza di insuccessi in tutti gli esperimenti precedenti. Dall’ipotesi di indipendenza si può facilmente determinare la probabilità che il tempo di primo successo T sia osservato in corrispondenza dell’esperimento k-esimo:
 

P(T=k)=(1-p)^k-1p

Poiché 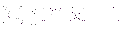, ne consegue che prima o poi il successo arriva, anche se p ha un valore molto piccolo! Per avere un’idea quantitativa di quanto occorra attendere per osservare il primo successo, si può utilizzare il valore medio di T che risulta:

E(T)=1/p.

Supponendo ad esempio che il rischio giornaliero di un incidente domestico sia pari a 10^-4, il tempo medio di attesa per un incidente risulta pari a circa 27 anni, che non è un tempo così lungo da non doversene preoccupare!
D’altra parte, il fatto che eventi rari prima o poi si verifichino potrebbe essere poco interessante ai fini pratici, se il tempo di attesa è molto elevato. Nel caso sopra citato, della lotteria annuale, la probabilità di vincere acquistando un biglietto, se la lotteria vende dieci milioni di biglietti è pari a p=10^-7 (dovendosi supporre che tutti i biglietti abbiano la stessa probabilità di essere estratti, altrimenti ci sarebbero gli estremi per azioni in sede giudiziaria!); supponendo che un individuo compri un biglietto tutti gli anni, il tempo medio di attesa per la sua vincita risulta pari a 10 milioni di anni, il che dovrebbe sconsigliarlo dallo spendere i soldi del biglietto!
Se poniamo una scimmia davanti alla tastiera di un computer e supponiamo che la scimmia batta a caso sulla tastiera, lo schema di Bernoulli ci dice che la scimmia finirà per scrivere la Divina Commedia, anzi la riscriverà infinite volte. Nella pratica, naturalmente, nessuno assisterà mai al primo successo della scimmia. Il che rimanda in sostanza al fatto che lo schema di Bernoulli, come ogni modello probabilistico, fornisce solo una approssimazione della realtà, che dobbiamo essere pronti a rivedere e raffinare.
Se la scimmia scrivesse al primo colpo la Divina Commedia, dovremmo probabilmente, prima di attribuire la cosa alla fluttuazione statistica, verificare se la scimmia non sia stata adeguatamente istruita (se pensiamo che ciò sia possibile). Più seriamente, se in una certa zona si verifica una maggiore incidenza di una certa malattia, occorre approfondire la questione per verificare se l’incidenza osservata possa essere attribuita al verificarsi di un evento raro ma non impossibile, oppure se occorra rivedere il modello coinvolgendo ad esempio fattori ambientali.

Dipendenza e indipendenza

Il verificarsi di un evento può modificare l’incertezza relativa al verificarsi di un altro evento. Se vediamo profilarsi all’orizzonte nuvole nere, l’incertezza sul verificarsi a breve di un temporale diminuisce; per restare al campo della meteorologia spicciola, anche il proverbio rosso di sera bel tempo si spera esprime in definitiva una modifica dell’incertezza sul tempo che si avrà domani in base al tempo osservato oggi.
Il Calcolo delle probabilità affronta situazioni di questo tipo attraverso la probabilità condizionata, definita come:

P(A|B) = P(AB) / P(B)

dove A e B sono due eventi ed ovviamente P(B)≠0. La probabilità condizionata è quindi la probabilità del verificarsi simultaneo di A e di B, “normalizzata” con P(B), il che rende ragionevole P(A|B) come misura dell’incertezza di A una volta che si sia osservato B. Se P(A|B)=P(A), il verificarsi di B non influisce sulla probabilità del verificarsi di A e quindi si può a ragione dire che A è indipendente da B; poiché si verifica immediatamente che in tale caso anche B è indipendente da A, quando P(A|B) = P(A) si dice che A e B sono indipendenti. Questa definizione di indipendenza, che a nostro giudizio meglio ne esprime il concetto intuitivo, è equivalente alla più tradizionale definizione che invoca l’uguaglianza P(AB) = P(A)P(B).
I problemi nei quali intervengono probabilità condizionate richiedono una particolare attenzione, in quanto spesso la prima risposta, guidata dall’intuizione, è quella sbagliata. Se cerchiamo di rispondere al quesito: il re proviene da una famiglia con due figli; quale è la probabilità che l’altro figlio sia sua sorella?, la risposta che viene più spontanea, ma che è errata, è 1/2. Per ottenere la risposta giusta, procediamo così: consideriamo gli eventi M=un figlio è maschio e F=un figlio è femmina e supponiamo che in ogni famiglia con due figli, o almeno nelle famiglie reali con due figli, il primogenito e il secondogenito siano maschio o femmina con probabilità 1/2. Poiché il quesito richiede di valutare P(M|F), ricorrendo alla definizione otteniamo:

P(M|F)=P(MF)/P(F)=(2/4):(3/4)=2/3.

L’ipotesi che due eventi siano indipendenti, come detto, significa che il verificarsi di uno dei due non modifica la probabilità del verificarsi dell’altro. Questo dimostra la fallacia di qualunque argomento volto a prevedere l’esito della prossima estrazione nel gioco del lotto in base all’esito delle precedenti estrazioni, in particolare considerando i numeri ritardatari. Sempre, naturalmente, che il gioco non sia truccato (come, per altro in passato, si è verificato in alcuni casi)!
La formula della probabilità condizionata permette di scrivere dopo qualche semplice passaggio:

Questa è la nota formula di Bayes (1702-1761), che lega la probabilità a priori P(A) alla probabilità a posteriori P(A|B).

Un tipico esempio di applicazione delle formula di Bayes è quello della diagnostica medica: se A è una malattia e B è un sintomo, possiamo ottenere la probabilità che, osservato il sintomo, si abbia la malattia, una volta date P(A) –che può essere ricavata dall’incidenza della malattia nella popolazione in esame, P(B|A), che esprime la probabilità che in pazienti malati si osservi il sintomo– e P(B|A), la probabilità che il sintomo sussista in assenza della malattia.

La formula di Bayes risulta uno strumento di utilizzo generale, che permette di trattare facilmente e rigorosamente diversi problemi probabilistici. Il noto dilemma del giocatore che si trova di fronte a tre porte, dietro a due delle quali c’è come premio una capra mentre la terza nasconde una automobile di lusso, e che, dopo avere scelto una porta (senza poterla aprire), viene “tentato” dal conduttore del gioco – dopo che questi ha aperto una seconda porta dietro alla quale c’è una capra – a cambiare la sua scelta iniziale, trova con la formula di Bayes una facile risposta: è vantaggioso per il giocatore cambiare la scelta.
L’utilizzo della formula di Bayes in Statistica come strumento per combinare le informazioni disponibili a priori su un fenomeno osservato con le informazioni fornite dai dati sperimentali, è alla base della statistica bayesiana, che sta riscuotendo negli ultimi decenni un crescente interesse [4].

Conclusioni

Lo sviluppo di un modello probabilistico permette il trattamento matematico dell’incertezza. Il modello permette di derivare conclusioni logiche e rigorose in base alle ipotesi formulate, evitando le trappole nelle quali è facile cadere procedendo in modo non rigoroso. Infatti, se da un lato è possibile trattare situazioni interessanti con una Matematica relativamente semplice e utilizzando concetti intuitivi, dall’altro l’affidarsi solamente all’intuizione può portare a conclusioni scorrette, come spesso capita all’“uomo della strada” quando si cimenta con giochi e lotterie. Come ogni modello matematico, anche il modello probabilistico è una astrazione e approssimazione della realtà.
Ne va pertanto verificata la attendibilità sulla base dei dati disponibili sulla situazione oggetto della modellizzazione, rivedendo il modello quando si riscontri lo scostamento
tra quanto da esso previsto e l’evidenza sperimentale. È compito della Statistica guidare questo processo di verifica e di revisione. Il lettore interessato ad approfondire gli argomenti qui trattati può consultare i trattati [5] e [6] e [7]. Per una introduzione elementare ricca di esempi, adatta anche ad un uso didattico in una scuola media superiore, si rimanda a [8]. Un classico trattato di Statistica, al quale si può fare sicuro riferimento, è costituito da [9].

Bibliografia

[1] A.I. Dale, Pierre-Simon Laplace. Philosophical Essay on Probabilities, Springer-Verlag, 1995

[2] A.N. Kolmogorov, Foundations of the Theory of Probability, Second English Edition, Chelsea, 1956

[3] B. de Finetti, Teoria delle Probabilità, I-II, Einaudi, 1970

[4] A. O’Hagan, J. Forster, Kendall’s Advanced Theory of Statistics - Vol. 2B - Bayesian Inference, Arnold, 2004

[5] G. Dall’Aglio, Calcolo delle Probabilità, Zanichelli, 2003.

[6] Y.S. Chow, H. Teicher, Probability Theory, Springer, 1997

[7] D.M. Cifarelli, Introduzione al calcolo delle Probabilità, McGraw Hill, 1998

[8] R. Isaac, The Pleasures of Probability, Springer- Verlag, 1995

[9] A.M. Mood, F.A. Graybill, D.C. Boes, Introduzione alla Statistica, McGraw Hill, 1997