L'Econometria
Introduzione

R.F.Engle e C.W.J Granger
Una recente occasione di attenzione nei confronti dell'Econometria è stata fornita dall'assegnazione del Premio Nobel 2003 per l'Economia a due econometrici, Robert F. Engle e Clive W.J. Granger. Non è la prima volta che il più alto riconoscimento in Economia viene assegnato a studiosi di questa materia (le precedenti occasioni sono una mezza dozzina)1. Tuttavia, questa occasione è particolarmente rilevante. I contributi di Engle e Granger hanno marcato indelebilmente lo sviluppo dell'Econometria delle serie macroeconomiche e finanziarie e stanno al contempo contribuendo a cambiare il modo con cui anche altre scienze applicate affrontano il problema della previsione temporale dei fenomeni e la costruzione di modelli interpretativi.
Ma che cos'è l'Econometria? Il termine non fa parte del lessico comune corrente. La stessa disciplina pare poco conosciuta. La scomposizione del termine nella radice econo- e in -metria porta spesso all'interpretazione (riduttiva) dell'Econometria come "scienza della misura dei fenomeni economici". Il Dizionario della lingua italiana Le Monnier definisce l'Econometria come l'"analisi quantitativa dei problemi economici, con larga applicazione di tecniche matematiche e statistiche". Anche se questa definizione descrive una parte significativa della disciplina, non dà ancora ragione compiutadella materia. Per tentare una prima definizione dell'Econometria, ne analizzeremo le relazioni con l'Economia; faremo poi riferimento allo statuto della Società scientifica internazionale che ne porta il nome; infine faremo ricorso ad alcune esemplificazioni dell'attività degli econometristi.
Economia ed Econometria
L'Econometria è coinvolta in ogni declinazione della teoria e della pratica economica, in cui occorra contemperare teoria e dati. Si occupa quindi di MicroEconomia, MacroEconomia, Economia finanziaria (solo per citare un primo livello di classificazione della teoria economica). Come noto, la MicroEconomia si occupa delle scelte individuali, ad esempio di consumo. La MacroEconomia si occupa delle scelte degli aggregati di soggetti economici, ad esempio delle relazioni fra consumo e reddito nazionale di una nazione. L'Economia finanziaria studia invece le relazioni micro e macro esistenti sui mercati finanziari.
Una diversa classificazione degli ambiti economici si ottiene sulla base del tipo di dati a disposizione. Quando i dati si riferiscono a diversi soggetti economici allo stesso istante di tempo, si parla di analisi e dati in cross-section. Quando invece i dati si riferiscono ad uno o più soggetti economici seguiti nel tempo, si parla di analisi e dati di serie storiche.
La classificazione sulla base dei dati è trasversale rispetto a quella basata su Micro, Macro e Finanza anche se, in prevalenza, l'Econometria delle serie storiche è stata dominante in Macroeconometria e quella cross-section in Microeconometria.
Una prima osservazione è che quindi vi sono diversi ambiti econometrici. La realtà economica – sempre più in rapida evoluzione – genera problemi, sia teorici sia applicati, sempre nuovi. Non sorprende quindi che molti problemi econometrici rimangano tuttora irrisolti.
L'Econometria è inoltre una scienza del futuro. L'Econometria si occupa infatti dei metodo e degli strumenti per affrontare decisioni in condizioni di incertezza. È facile prevedere, quindi, che sia destinata a essere sempre più l'elemento caratterizzante (o uno dei principali) nella formazione di molte professioni economiche del presente e del futuro.
Per meglio comprendere il futuro, volgiamo innanzitutto lo sguardo al passato e, in particolare, alla data di fondazione della Società di Econometria.
Una scienza di confine
La nascita dell'Econometria è di solito fatta coincidere con la fondazione dell'Econometric Society nel dicembre 1930 a Cleveland (USA) e dell'associata rivista Econometrica nel 1933. Nel primo numero di Econometrica (oggi accessibile anche via web sul sito della Società www.econometricsociety.org) si trova il primo articolo sulla costituzione della Società, che dà anche una definizione dello stesso termine Econometria.
La Società di Econometria è una società internazionale per l'avanzamento della teoria economica nella sua relazione con la statistica e la matematica. (...) L'obiettivo principale [della Società] è quello di promuovere studi che perseguano l'unificazione delle impostazioni teorico-quantitative e empirico-quantitative nella soluzione dei problemi economici e che siano permeati da pensieri costruttivi e rigorosi simili a quelli che sono diventati dominanti nelle scienze naturali. Ogni attività che promette in definitiva di migliorare tale unificazione degli studi teorici e fattuali in Economia sarà nella sfera di interesse della Società. [1]
Lo scopo dichiarato dell'Econometric Society
mette subito in evidenza gli stretti rapporti in Econometria fra teoria economica, Matematica, Probabilità e Statistica. È una curiosa coincidenza il fatto che il 1933 sia anche l'anno della prima formalizzazione rigorosa – dovuta a Kolmogorov – della nozione di probabilità sigma additiva, spesso citata come data di nascita della Probabilità moderna.
L'Econometria è quindi una scienza di confine, in cui gli strumenti matematici e statistici sono ampiamente applicati. Al contempo, però, i dati economici richiedono lo sviluppo di nuovi concetti e modelli matematici e statistici; l'Econometria si occupa dello sviluppo di nuove tecniche. I contributi di Engle e Granger sono proprio di questo tipo, con la definizione di nuove classi di modelli per cui sono state sviluppate tecniche di inferenza statistica. Queste stanno trovando applicazione in svariate Scienze naturali, dalla Geofisica all'Ecologia.
L'anelito all'unità che traspare dagli scopi della Società pare in contrasto con la deriva verso una crescente specializzazione (e parcellizzazione) della scienza. Questo anelito è tuttora molto moderno e sempre più necessario per poter comprendere i fenomeni economici.
L'Econometria aspira quindi a dare risposte scientificamente fondate e rigorose a quesiti economici che hanno una immediata rilevanza pratica nella vita della società. Nel seguente paragrafo si daranno alcuni esempi.
Econometria: a che serve?
Ecco alcuni quesiti che trovano nell'Econometria il metodo di soluzione:
- Qual è un intervallo probabile dei valori del tasso di inflazione (o della crescita del prodotto interno lordo, PIL) in Italia il prossimo anno?
- Quali sono gli effetti sull'inflazione e sul PIL dell'incremento di un punto percentuale del tasso di interesse di riferimento praticato dalla Banca Centrale Europea? Quali gli effetti di un taglio delle aliquote fiscali?
- Quali prodotti è più opportuno scegliere in una catena di supermercati come prodotti civetta? Di quanto è sufficiente abbassarne il prezzo per attirare (almeno) un dato numero di nuovi clienti con probabilità fissata?
- Esistono strategie di investimento borsistico "vincenti", ossia che danno profitti maggiori di quelli registrati in media dal mercato? Dato un certo portafoglio titoli in un determinato giorno, è opportuno ri-bilanciare le quote investite nei vari titoli alla luce dell'informazione sopraggiunta sul mercato?
Ciascuno dei quesiti sopra riportati rappresenta una diversa classe di problemi: rispettivamente, la previsione; l'interpretazione dei nessi causali e della dinamica in un sistema economico; il marketing; le scelte di portafoglio in finanza.
La risposta a ciascuno di loro non può essere unica o univoca. La probabilità, di cui al punto 1, dipende dallo stato dell'Economia italiana e dalle informazioni a disposizione di chi formula la previsione. Le risposte al quesito 2 dipendono dall'Economia e dal periodo temporale oggetti di interesse. Analoghe considerazioni valgono per i quesiti 3 e 4. In Economia, infatti, i soggetti economici sono quasi sempre diversi fra loro, oltre che operanti in condizioni sempre differenti. Non è quindi possibile pensare di calcolare costanti cosmologiche in Economia, come ad esempio la velocità della luce in Fisica. L'Econometria fornisce quindi il metodo di soluzione, più che risposte numeriche universalmente valide.
Metodi e modello
Il metodo econometrico è mediato dalla costruzione di un modello, basato sulle informazioni (ossia i dati) disponibili al decisore. La nozione di modello econometrico è centrale nella disciplina e coincide, in prima istanza, con l'idea di modello statistico. Il modello è costituito dalla classe di processi stocastici fra i quali si ritiene sia compreso quello, detto processo di generazione dei dati (DGP in inglese), che ha effettivamente generato i dati a disposizione.
Per meglio chiarire il problema si consideri l'esempio 3 della sezione precedente. La teoria microeconomica prevede che una possibile funzione di domanda di un agente rappresentativo r del bene 1 sia della forma
ln qr(1) =γ1+γ2ln yr +Σj=in βj ln pr(j)
dove pr(j), qr(j), sono prezzi e quantità del bene j osservati e richiesti rispettivamente dall'agente economico r, e yr è la spesa totale dello stesso agente.
Supponiamo ora di avere a disposizione i dati delle fidelity card di un supermercato relative a spesa totale yi e singole spese qi(j) per un determinato numero di occasioni di acquisto, insieme ai dati sui prezzi pagati, i=1, ..., n. Nel seguito si ipotizza che ogni occasione di acquisto i corrisponda a un diverso consumatore. Con questi dati, il modello micro è annidabile in un modello di regressione del tipo:
ln qi(1) =γ1+γ2ln yi +Σj=in ηj ln pi(j)+ui=β'xi+ui
dove l'i-esimo agente è assunto discostarsi dal comportamento dell'agente rappresentativo r per effetto di un errore casuale ui. I coefficienti β possono essere stimati con il metodo dei minimi quadrati, producendo gli stimatori β.
I termini ui e uj (relativi a due diversi agenti) sono in genere considerati stocasticamente indipendenti e identicamente distribuiti (iid): gli scostamenti dell'agente i e j dal comportamento dell'agente rappresentativo r non sono correlati e hanno la stessa distribuzione. In seguito chiamiamo questa assunzione ipotesi iid.
Per modello di regressione, si intende l'equazione (1) con un insieme di ipotesi associate, che tipicamente include l'ipotesi i.i.d. per l'errore ui. Per la Microeconometria, le quantità di interesse sono le costanti γ2 e βi, che corrispondono alle elasticità della domanda del bene 1 rispetto alla spesa totale e ai prezzi. Per queste la microeconomia dà predizioni (per esempio) sul segno, ma non sui singoli valori. Il modello di regressione permette invece di stimare i coefficienti γ2 e βi, rendendo operativa la teoria micro. Questo passaggio è fondamentale, per esempio, per la soluzione del problema di marketing all'esempio 3.
Test delle teorie
Negli anni '40, l'Econometria visse una fase di intensa crescita e di confronto con l'Economia teorica. È questo il periodo più fervido di attività presso la Cowles Commision, fondazione di ricerca econometrica situata allora presso l'Università di Chicago che risolse i problemi di stima del modello a equazioni simultanee2. Lo scopo della ricerca econometrica era ambizioso: il test (delle implicazioni) delle teorie economiche, trattato come un problema di inferenza statistica.
Questa posizione è ben rappresentata da un famoso articolo del 1944 su Econometrica di T. Haavelmo, premio Nobel 1989 [2].
Per illustrare lo spirito di questo programma di ricerca, facciamo uso dell'ipotesi microeconomica che la funzione di domanda sia del tipo esposto nel paragrafo precedente. L'esempio ci permette di evitare la complessità delle equazioni simultanee, proponendo l'aspetto essenziale dell'idea del test delle teorie economiche.
Si consideri, ad esempio, il modello di regressione (1) e l'ipotesi γ2=1. Questa può essere considerata un test della corrispondente teoria microeconomica. Il test saggia congiuntamente la predizione microeconomica e le assunzioni del modello di regressione. Se queste ultime non vengono rispettate, il test dell'ipotesi in questione potrebbe portare a un rifiuto, non per fallacia della teoria economica, ma per incongruenza del modello statistico con i dati. La necessità di saggiare congiuntamente ipotesi economiche e ipotesi statistiche non è presente nelle scienze sperimentali, dove la corretta programmazione dell'esperimento garantisce la validitàdelle assunzioni del modello di regressione per costruzione3. Le scelte dei consumatori della catena di supermercati, monitorati ormai in modo continuo attraverso le fidelity card, sono invece operate ai prezzi di mercato e non a quelli ipotetici scelti arbitrariamente dallo sperimentatore. Anche i prezzi azionari sono raccolti per osservazione passiva, così come l'inflazione e il PIL nel primo esempio del paragrafo 3. Una caratteristica comune di questi esempi è quindi quella di essere il risultato di esperimenti naturali, non programmati come in laboratorio. Questo è uno degli aspetti peculiari delle scienze economiche.
È opinione di un altro premio Nobel (1980), Lawrence Klein, anch'egli proveniente dalla Cowles Commission, che dal contributo di Haavelmo in poi l'Econometria sia diventata "una branca specializzata della Statistica matematica, che si occupa dell'inferenza statistica per dati non sperimentali" [3, p. 415]. Klein fu il più giovane dei ricercatori della Cowles Commission negli anni Quaranta. Di interessi soprattutto applicativi, portò avanti la linea di ricerca della Cowles Commission stimando negli anni Cinquanta e Sessanta molti modelli macroeconomici e guidando il progetto LINK per il collegamento dei vari modelli macroeconomici nazionali in un modello mondiale dell'Economia. Il suo giudizio sulla matematicizzazione dell'Econometria, pronunciato forse in modo provocatorio, per un pubblico di economisti, pare non lontano dal vero e tutt'altro che offensivo.
Esperimenti ripetuti e esperimenti naturali
Da Galileo, in poi, il ruolo dell'esperimento è centrale nella moderna nozione di scienza. La ripetibilità dei risultati è il requisito sine qua non per le scienze naturali. In Economia invece i dati non sono frutto di un esperimento programmato e ripetibile. (L'introduzione in Economia di esperimenti veri e propri è infatti recente; questa branca dell'economia è chiamata "Economia sperimentale". A questa viene rivolta molta attenzione e credito, ma anche la critica di non saper replicare fedelmente le condizioni osservate nelle economie reali).
Il consumo aggregato di una nazione in un determinato anno è da considerarsi la realizzazione di un esperimento in cui i consumatori hanno operato scelte di consumo e di risparmio coerenti con il proprio reddito disponibile corrente, la propria ricchezza e una serie di altri fattori economici (preferenze, teconologia, aspettative) e di composizione demografica presenti in quell'anno e, in generale, non ripetibili in altri anni.
L'assunzione tipica relativa a dati di esperimenti ripetibili –la misura ripetuta della distanza fra due corpi celesti, di un peso molecolare, del pesotipo di un animale ecc. – è quella di osservazioni indipendenti e identicamente distribuite (iid). È questa l'assunzione che caratterizza campioni casuali semplici, quelli cioè estratti (con ripetizione) casualmente da un'urna contenente tante etichette tutte uguali, ciascuna corrispondente a un elemento della popolazione da cui estrarre il campione.
Data la natura non sperimentale di tanti dati economici, l'assunzione iid non può essere adottata nell'analisi di questi dati. Il problema di come analizzare i dati economici non sperimentali ha motivato e caratterizzato la ricerca econometrica fin dagli inizi. La necessità di lavorare su come analizzare i dati piuttosto che su come produrli è una delle caratteristiche peculiari dell'Econometria.
La regressione spuria
Un esempio delle difficoltà create dall'assunzione iid è dato da alcuni esempi del cosiddetto problema della correlazione spuria, già ben noto all'atto della creazione della Società di Econometria, come testimonia un articolo di G. U. Yule del 1926 [4].
Yule prese spunto, nel suo studio, dall'alta correlazione (positiva) registrata fra la frazione di matrimoni di rito anglicano(yi), sul totale dei matrimoni, e il tasso di mortalità standardizzato (xi) in Inghilterra negli anni 1866-1911, per un totale di n=46 osservazioni.
La correlazione calcolata, pari a 0.9512, risultava significativa quando si calcolava il testt nella regressione di yi su xi, ossia se si adattava un modello lineare del tipo:
yi=α+βxi+ε, (2)
con le assunzioni associate.
Yule considerava questa relazione positiva del tutto priva di senso: come potevano essere associati il tasso di mortalità con la frazione di matrimoni religiosi? Come poteva un numero minore di matrimoni di rito religioso essere collegato alla minore mortalità? Doveva trattarsi di una relazione spuria che, però, invece di produrre solo facili umorismi, aveva bisogno di trovare una spiegazione scientifica.
Se nel modello di regressione (2) si ipotizza che zt :=(yt : xt)' siano iid, effettivamente si arriva a conclusioni "strane", non suffragate da alcuna spiegazione causale derivante da una teoria socio-economica plausibile.
Oggi è semplice osservare che queste conclusioni sono essenzialmente basate sull'ipotesi - insostenibile - che le osservazioni del vettore zt :=(yt : xt)' siano iid al variare del tempo t. I dati sui matrimoni e sulla mortalità (zt)t=1 T sonola realizzazione di un esperimento sequenziale dove giocano fenomeni socio-economici di lungo periodo (di calo dei matrimoni e miglioramento delle condizioni di vita) che invalidano l'assunzione iid.
La comprensione piena del fenomeno della correlazione spuria è dovuta a Peter Phillips, grazie a un lavoro pubblicato nel 1986 [5]. Sul questo tema ha lavorato anche Granger; si può argomentare che la risposta più completa al problema della regressione spuria sia costituita dalla nozione di cointegrazione, introdotta all'inizio degli anni ottanta da Granger, che gli ha fruttato il premio Nobel. La nozione combina l'aspetto di relazione fra fenomeni e la presenza di trend nelle serie temporali economiche.
Due ubriachi e la cointegrazione
Un aspetto tipico dell'analisi econometrica, presente anche nel problema della correlazione spuria, è l'enfasi sull'analisi del legame fra variabili economiche (ancor prima che lo studio di un fenomeno economico isolato nel tempo). L'Econometria è per elezione votata all'aspetto multivariato dell'analisi statistica. Questa caratteristica, presente negli esempi 1-4 del paragrafo 3, è abbastanza peculiare dell'Econometria (e dell'Economia).
Nelle scienze naturali – in Chimica, per esempio – può essere interessante sapere come si evolve una certa concentrazione in una reazione chimica, inmodo isolato da qualsiasi altro aspetto del fenomeno. In Economia nonè invece possibile definire l'evoluzione del tassodi inflazione in ambiente isolato, perché i prezzi sono generati in un'economia dove si scambiano beni e non possono essere discussi senza le quantità e diversi agenti.
Per introdurre il concetto di cointegrazione, usiamo l'esempio dei due ubriachi "a braccetto".
Si indichino con A e B i due ubriachi e con t = 0, 1, ... il tempo a partire dall'uscita dal bar (corrispondente all'istante t = 0). Siano inoltre zt e st le distanze in linea d'aria rispettivamente di A e B dal bar, misurate nella direzione di casa che si assume sia comune ad A e B. La distanza iniziale dal bar è quindi nulla per A e B, z0=s0=0. Si indichino inoltre con ut e vt gli spostamenti, ossia i "passi", di A e B all'istante t.
Si assuma che l'ubriaco A segua una passeggiata casuale unidimensionale, zt= zt-1+ut e che tenga a braccetto B, attirandolo a sé prima di ogni passo in modo che il punto di partenza di B all'istante t sia proporzionale a quello di A: st= zt-1+vt γ è una costante di proporzionalità. Se, ad esempio è γ=1, i due ubriachi muovono entrambi da zt-1. Si assume nel seguito che e't= (ut, et) sia i.i.d. a media nulla e che la matrice di varianza Ω=E(et e't)=[σij] ,i,j= u, v, sia positiva definita. Le due equazioni possono essere riassunte nella seguente notazione matriciale, detta rappresentazione autoregressiva:
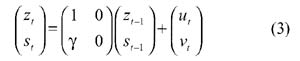
Ossia:
wt=A1wt-1+et
Una simulazione del sistema è riportata nella figura 1.
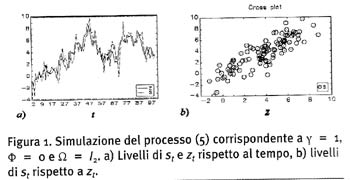
Si osservi come il processo (5), sia non-stazionario, in quanto zt segue una passeggiata casuale univariata, Σi=1tui+z0 dove z0=0. Si indichi con gt=Σi=1tui la passeggiata casuale. Vogliamo ora ricavare come gt sia la componente comune del sistema. Infatti è st=γgt+ (vt–γut) e vale la seguente rappresentazione a trend comuni:
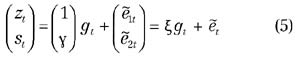
Entrambe le componenti di wt condividono la stessa componente non-stazionaria gt,chiamata pertanto trend comune nel sistema wt (3),(4). Poiché gt è una componente integrata, il sistema w, si dice cointegrato. Essa scompone wt in una parte non stazionaria comune gt (permanente) e nella componente residuale stazionaria (transitoria) e',. Nell'esempio dei due ubriachi gt rappresenta la passeggiata casuale comune ad A e B.
Si osservi che la matrice ξ nella (5) ha rango 1 e può essere annullata pre-moltiplicando per un qualsiasi vettore β appartemente allo spazio nullo di col(ξ). Pertanto, una proprietà caratterizzante di un sistema cointegrato è che: esiste almeno una combinazione lineare delle variabili del sistema che risulta stazionaria; i coefficienti di tali combinazioni lineari si diconovettori di cointegrazione. Nel caso precedente β puo' essere scelto come β=(γ, -1)'.
Il teorema di rappresentazione dovuto a Granger stabilisce anche la corrispondenza di un sistema cointegrato con un modello a correzione dell'errore. Si consideri nuovamente la rappresentazione autoregressiva (6) e si sottragga wt-1 da ambo i membri. Si ottiene così:
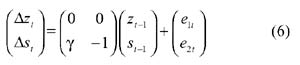
o
Δwi=αβ'wt-1+ et.
dove α=(0, 1)' e β=(γ, -1) e Δzt:=zt–zt-1. Questa formulazione è chiamata a correzione dell'errore (ECM). Infatti il termine (β'wt-1 misura la deviazione (errore) di β'wt-1 dal proprio valore atteso 0, interpretato come valore di riferimento. L'eq. (6) esprime la reazione di Δwt a deviazioni dall'obiettivo β'wt-1 mediantei coefficienti di aggiustamento α. Nei termini del β'wt-1=γzt–st rappresenta una distanza (segnata) degli ubriachi, che questi tendono a riportare verso 0, in quanto A attira a sé B prima di ogni passo.
La nozione di cointegrazione ha trovato favore in Economia anche in ragione della possibilità di distinguere relazioni di breve e lungo periodo. Altre teorie economiche sono basate sulla classificazione delle fluttuazioni in permanenti e transitorie.
Questi concetti – i primi di natura economica, i secondi di natura statistica – possono essere messi in relazione fra di loro secondo lo schema della tabella seguente.
| Nozioni economiche | Nozioni statistiche |
|---|---|
| fluttuazioni permanenti | processi non-stazionari |
| oscillazioni transitorie | processi stazionari |
| equilibri di lungo periodo | relazioni di cointegrazione |
Le associazioni presentate nella tabella possono essere così giustificate.
- I processi (AR) stazionari oscillano attorno al proprio valore atteso piuttosto rapidamente; eventuali scostamenti dalla media sono quindi transitori;
- quando una passeggiata casuale (processo integrato) raggiunge un certo livello, non vi è alcuna tendenza a ritornare verso il punto di partenza o a spostarsi verso un diverso livello di riferimento; pertanto per tali processi ogni spostamento è permanente;
- l'esistenza di relazioni lineari (relazioni di cointegrazione) fra processi non-stazionari è simile all'idea di equilibrio fra variabili economiche; scostamenti da tali relazionisono processi stazionari, ossia di natura transitoria.
Questa giustapposizione di nozioni di ambito stocastico ed economico ha favorito il diffondersi delle tecniche di cointegrazione ([9], cap. 7, vol II).
Un ubriaco e la passeggiata casuale
Uno dei più semplici processi stocastici è costituito dalla passeggiata casuale, che deriva il proprio nome dalla metafora di un ubriaco (di cui si segue la distanza dal bar nel rientro verso casa).
Sia xt tale distanza, dove t indica il tempo che assume valori discreti: t=0,1,2, ... Al tempo 0, ossia all'uscita dal bar, è x0=0. Il primo passo, di intensità ε1, porta l'ubriaco nella posizione x1=x0+ ε1=ε2.
L'ubriaco è tale perché l'intensità del passo εt è una variabile aleatoria, con media o. Pertanto, a ogni passo, l'ubriaco può allontanarsi dal bar nelle due direzioni. Il processo {εt}t=1∞ è ipotizzato i.i.d. ossia i passi sono indipendenti gli uni dagli altri e hanno la medesima distribuzione. Al tempo 2, l'ubriaco si trova nella posizione x2=x1+ε2=Σt=12εt; al tempo 3 nella posizione x3=x2+ε3=Σt=13εt e, in generale:
xt=Σi=1tεi
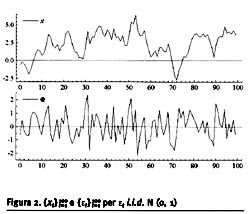
Ciascun passo è cumulato nel valore corrente. Una realizzazione di un processo così fatto è rappresentata nella figura 2, dove si raffigurano {xt}t=1100 e {εt}t=1100 per εt i.i.d. N (o, i). Si osservi l'erraticità di {εt}t=1100 e la persistenza della passeggiata casuale corrispondente xt. Le passeggiate casuali replicano caratteristiche di persistenza osservate nelle serie storiche economiche.
Conclusioni
L'econometria è — per sua vocazione — disciplina rivolta al-le applicazioni economiche. Queste stanno crescendo in numero e difficoltà, sia dal punto di vista interpretativo, che calcolatorio, grazie alle sempre maggiori fonti di dati. I problemiche questi dati non sperimentali pongono sono sempre nuovi, e se alcuni – come quelli che hanno portato alla scoperta della cointegrazione – hanno trovato risposta, altrettanti aspettano di essere affrontati e risolti.
Dal punto di vista occupazionale, gli econometristi trovano ampi spazi nel mondo del lavoro. In futuro ci si attende un ulteriore incremento delle professioni che fanno dell'econometria una conoscenza caratterizzante. In questo senso, l'econometria è una disciplina del futuro.
Granger e l'invenzione della cointegrazione

Clive W.J. Granger riceve il premio Nobel
Clive Granger è una delle figure più rappresentative della professione econometrica. Nato a Swan Sea nel Galles (UK) il 4 settembre 1934, Si iscrisse al neonato e innovativo (in Inghilterra per quei tempi) corso in Economia e matematica all'Università di Nottingham. La scelta era motivata dal desiderio di "trovare un'area della matematica applicata che fosse di aiuto o utile in qualche senso" [7, p 255]. Per le sue attitudini, fu ben presto convinto a passare alla laurea in Matematica, che conseguì nel 1955, sempre con la speranza di concludere anche gli studi di Economia. Si iscrisse così al programma di dottorato in Statistica presso il Dipartimento di Matematica di Nottingham. Prima ancora di terminare il dottorato, conseguito nel 1959, fu selezionato come lecturer in statistica presso lo stesso Dipartimento.
In una fase di espansione globale dell'Università inglese del tempo, come unico statistico dell'Università, venne a contatto con molte discipline e molti tipi di dati diversi a causa dei molti colleghi che lo contattavano per analizzare i propri. Fu questo il miglior completamento della sua formazione, dirà poi Granger. Nella ricerca di un campo di interesse di rilevanza in Economia, Granger osservò che la maggior parte dei dati disponibili in Economia erano allora dati in serie temporali, ma che nella biblioteca dell'università vi era un unico volume sulle serie storiche economiche. Scelse quindi di occuparsi di questo tema. Nel contempo, ottenne una borsa di ricerca per un periodo di ricerca negli USA. Delle due risposte positive alla sua richiesta di passare un periodo di ricerca come visitatore, dalla Cowles Commission a Vale e da Princeton, scelse la seconda in quanto Oscar Morgenstern (uno dei padri fondatori della Teoria dei giochi) lo invitò a far parte di un gruppo di ricerca sulle serie storiche. Il gruppo era composto da M. Hatanaka e Granger, supervisionati, da John Tuckey (altra figura eminente in Statistica). Il gruppo studiò i metodi spettrali, che applicano l'analisi di Fourier allo studio delle serie storiche economiche. Di quel periodo, Granger ricorda l'idea dell'uso del cross-spectrum come l'idea fondante, che riflette la caratteristica tipicamente econometrica dell'enfasi sulle relazioni fra variabili (più ancora che sull'analisi univariata dei fenomeni).
Il periodo di ricerca a Princeton mise in contatto Granger con la comunità scientifica statunitense. Questi contatti lo portarono nel 1974 a trasferirsi in California, a San Diego, dove contribuì a fondare uno dei Dipartimenti di Economia più noti in ambito econometrico (di cui fece ben presto parte anche Rob Engle). Quando, alla fine degli anni Settanta, si trovò a decidere se rimanere a San Diego, l'Inghilterra era nel pieno della diaspora universitaria causata dai tagli alla spesa pubblica apportati dalla riforma Thatcher.
Nel periodo in cui Granger visse in Inghilterra, ebbe molti contatti con la London School of Economics, uno dei maggiori centri di ricerca econometrica fondata da Dennis Sargan. Fra i diversi eminenti allievi di Sargan, si segnalò negli anni Settanta la figura di David Hendry. Egli introdusse in modo sistematico il modello a correzione dell'errore nello studio della funzione del consumo aggregato alla fine degli anni Settanta.
L'idea della cointegrazione sorse proprio in una discussione fra David Hendry e Clive Granger. Hendry sosteneva, sulla base della ricerca empirica sul modello a correzione dell'errore, che è possibile che due serie yt e xt siano I (1) e che la loro differenza yt-xt sia stazionaria. Granger sosteneva il contrario perché la proprietà di integrazione è dominante, e si ripromise di dimostrare che Hendry aveva torto. Invece, riuscì a dimostrare che Hendry aveva ragione. Nacque così la cointegrazione. Granger dimostrò nel 1981 una versione del teorema che oggi si chiama Teorema di rappresentazione di Granger, poi migliorato e discusso in molte versioni.
L'articolo che dette inizio alla letteratura sulla cointegrazione è una versione ampliata del manoscritto di Granger del 1981, che apparve solo nel 1987 su Econometrica [10].
Il teorema di rappresentazione di Granger chiarisce che la nozione di cointegrazione implica ed è implicata dall'esistenza di un modello a correzione dell'errore per processi I (1). Inoltre, è semplice osservare che la nozione di cointegrazione è associata a una struttura di trend comuni del sistema. Queste diverse rappresentazioni sono evocative di diverse idee comuni in Economia. Ad esempio, il concetto di crescita economica bilanciata è omologa a quella di trend comuni. Similmente, le relazioni stazionarie fra variabili contenenti trend bene si sposano con l'idea di equilibrio economico: la relazione stabile rappresenta l'equilibrio di lungo periodo attorno a cui fluttuano le variabili, creando un disequilibrio transitorio. Il modello a correzione dell'errore, oggi chiamato a correzione verso l'equilibrio, spiega come questi errori sono compensati, ossia come il sistema torni verso l'equilibrio una volta allontanatosi da questo.
Granger ha associato il proprio nome a molti altre aree di ricerca nell'Econometria delle serie storiche (quali l'analisi spettrale, la regressione spuria, la nozione di causalità, l'impostazione decisionale nella teoria delle previsioni). Ha fatto parte del Dipartimento di Economia di San Diego fino all'età della pensione, che ha da poco raggiunto dal punto di vista anagrafico.
Rimane però molto attivo in ambito di ricerca e non è difficile incontrarlo nei corridoi di qualche riunione scientifica dell'Econometric Society in diverse parti del mondo anche quando (raramente) il suo nome non compare fra le relazioni invitate. Il suo sito personale si trova all'indirizzo internet:
http: //www.econ.ucsd.edu/˜cgranger/.
NOTE
1 James J. Heckman e Daniel L. McFadden nel 2000, Trygve Haavelmo nel 1989, Lawrence R. Klein nel 1980, Leonid Vitaliyevich Kantorovich e Tjalling C. Koopmans nel 1975, Ragnar Frisch e Jan Tinbergen nel 1969. Anche i Nobel del 1984 a Richard Stone e del 1973 Wassily Leontief possono essere classificati in parte come Nobel econometrici, in base alla forte connotazione quantitativa dei contributi di questi economisti.
2 Per un'esposizione dell'attività e del ruolo della Cowles Commission nello sviluppo dell'econometria, si veda Epstein [6].
3 Su questa relazione fra modello, parametri e test della teoria economica si incentrò un vivace dibattito fra economisti quali J. M. Keynes ed econometristi, quali J. Tinbergen e i membri della Cowles Commission negli anni quaranta. Gli economisti teorici sosteneva che i modelli sul ciclo economico di Tinbergen erano "misure senza teoria". Gli econometristi contrapponevano la critica agli economisti teorici di produrre "teorie senza misura". Per una rassegna di questa diatriba e sui suoi effetti sull'econometria si veda ancora [6].
BIBLIOGRAFIA
[1] Frisch R. (1933) Editor's note, Econometrica 1, 1-4.
[2] Haavelmo T. (1944) The probability approach in econometrics, Econometrica, 12 (supplement)
[3] Klein L. R. (1971) Whither Econometrics? Journal of the America) Statistical Association 66, 415-421
[4] Yule G.U. (1926) Why do we sometimes get nonsense correlation between time-series? A study in sampling and the nature of time-series, Journal of the Royal Statistical Society 89, 267-298
[5] Phillips P.C.B. (1986), Understanding spurious regression in econometrics, Journal of Econometrics 33, 311-340.
[6] Epstein R. J. (1987) A history of econometrics, North Holland
[7] Phillips P.C.B. (1997), The ET interview: Professor Clive Granger, Econometric Theory 13, 253-303.
[8] Diebold F. (2003) The ET interview: Professor Robert F. Engle, Econometric Theory 19, 1159-1193.
[9] Gardini A. et al. (2000), Econometria, vol. I e Il, Franco Angeli editore
[10] Engle R.F. e C.W.J. Granger (1987,) Cointegration and Error Correction: Representation. Estimation and Testing. Econometria 55 : 251-276.
