Leonhard Euler: vita e pensiero

Introduzione

Eulero

Quando l'Illuminismo europeo ebbe origine, intorno agli anni '20 del 1700, in matematica si attendevano pochi risultati nuovi. Anche se nel secolo precedente, quando la maggior
parte dei suoi praticanti proveniva dall'aristocrazia o da professioni legali o mediche, la Matematica non era ancora diventata una professione, quel periodo, culminato con le invenzioni del Calcolo differenziale da parte di Isaac Newton e Gottfried Leibniz, era considerato una grande età per la matematica, che aveva lasciato poco da scoprire. Ma alcuni studiosi previdero un periodo fecondo per il settore[1]. Soprattutto le ricerche di Leonhard Euler ne avrebbero dimostrato la correttezza. Lo svizzero Euler sarebbe diventato uno dei quattro maggiori matematici della storia, gli altri tre essendo Archimede, Newton e Carl Friedrich Gauss. Solo a Newton ed a Euler, Gauss riservava il termine di summus[2].
Guidato dalla passione per la Matematica e le scienze naturali, dall'impegno di costruire per esse una solida base istituzionale e da un'insistente difesa della riforma cristiana, Euler ha dato contributi a tutta la scienza matematica ed è stato senza dubbio il più prolifico matematico della storia. Nel cuore della sua ricerca si trovano l'Analisi infinitesimale, o Calcolo differenziale, e la Meccanica razionale. Insieme alla meccanica celeste, le fece diventare la scienza par excellence del XVIII secolo. Fu il principale creatore dal Calcolo delle variazioni e delle equazioni differenziali, ed un precursore della Geometria differenziale delle superfici. In Meccanica, Euler, non Newton, formulò la maggior parte delle equazioni differenziali prima di William Rowan Hamilton. Alle prese con la concorrenza interna dell'Illuminismo, in questo caso da parte di Jean d'Alembert, Alexis Clairaut, Daniel Bernoulli e Colin Maclaurin, permise di trasformare la meccanica e l'astronomia in moderne scienze esatte, basate sul calcolo infinitesimale. Euler fondò la meccanica dei continui, inoltre promosse la balistica, la cartografia, la diottrica, la teoria dell'elasticità, l'idraulica, l'idrodinamica, la teoria della musica, la teoria dei numeri, l'ottica e la teoria delle navi. Il suo lavoro è caratterizzato da massicci ed audaci calcoli, da una straordinaria applicazione dell'analisi e dell'analogia, dal ricorso al suo infallibile istinto e da chiarezza nella scrittura. Dai tempi di Claudio Tolomeo, nessun geometra aveva dominato tutti i rami della matematica. Nel corso del XVIII secolo, quattro istituzioni scientifiche reali, a Parigi, Londra, San Pietroburgo e Berlino, oscuravano le università nella ricerca scientica.

È soprattutto grazie al lavoro di Euler che le accademie scientifiche di San Pietroburgo e di Berlino divennero preminenti centri europei. I piµu che 810 fra i suoi articoli e libri, che riempiono 74 grossi volumi nelle prime tre serie della sua Opera Omnia, comprendono all'incirca un terzo di tutte le ricerche di matematica, fisica teorica ed ingegneria meccanica pubblicate dal 1726 al 1800, mentre la sua enorme corrispondenza riempie l'equivalente degli articoli[3].

Famiglia, gioventù ed educazione formale

Leonhard Euler nacque a Basilea, Svizzera, il 15 aprile del 1707. Mentre la maggior parte dell'Europa protestante ed ortodossa seguiva il calendario Giuliano, o del vecchio stile, dal 1701 la città aveva adottato l'attuale calendario Gregoriano. La casa natale di Euler era probabilmente situata nel quartiere attorno alla chiesa di St. Martin, vicino al centro ed alla zona di mercato ed approdo al fiume Reno.

Egli era il primo figlio di Paul Euler, ministro della chiesa evangelica riformata, e di Margaretha Bruckner. Mentre "riformata" si riferiva in generale al protestantesimo di Calvinisti e Luterani, la variante di Basilea era di un pietismo che accentuava l'amore e la vita interiore. La madre di Leonhard, Margaretha, figlia di un altro ministro protestante, discendeva da una illustre famiglia di artisti e umanisti. Il loro figlio fu battezzato due giorni dopo la nascita nella stessa Martinskirche dove anche suo padre era stato battezzato.
Leonhard non passò la prima giovinezza a Basilea. Nel giugno del 1708, suo padre divenne pastore della chiesa di St. Martin nei pressi di Riehen-Bettigen. A novembre si trasferì con la famiglia a Riehen, circa cinque chilometri a nord-est di Basilea. Gli Euler vivevano in una casa parrocchiale di due stanze che fu ampliata nel 1712. Una stanza serviva da studio, l'altra come abitazione. Delle due sorelle minori di Leonhard, Anna Marie era nata nel 1708 e Marie Magdalena nel 1712. Johann Heinrich, il quarto figlio degli Euler non nacque prima del 1719, quando il fratello maggiore era ormai partito per studiare al Gymnasium di Basilea. Leonhard era un ragazzo intelligente, a quanto pare allegro e socievole. La semplicità della vita di campagna, insieme al modello dei suoi genitori, troverà riflesso nella schietta natura e perfino nella disponibilità dell'Euler adulto.
I genitori di Leonhard furono i suoi primi insegnanti. Sua madre Margaretha, di tradizione umanistica, lo introdusse ai classici greci e romani. L'istruzione elementare di suo padre Paul comprendeva la Matematica, intesa come materia alla base di ogni conoscenza naturale. Paul non cominciò con un testo di geometria, bensì con la Coss o Algebra, di Christoff Rudolff, l'equivalente tedesco dell'italiano cosa o incognita, un lavoro in due parti che Michael Stiefel aveva esteso da 208 a 484 pagine. Nella sua autobiografia incompiuta, Euler ricorda di aver studiato diligentemente il testo per parecchi anni, facendo progressi nella soluzione dei suoi 434 problemi, la maggior parte dei quali erano equazioni di primo o di secondo grado[4]. Ciò avvenne prima che si trasferisse a Basilea presso la nonna materna per iscriversi al locale Gymnasium, probabilmente all'età di otto anni. Solo un ragazzo eccezionale a quell'età poteva fare progressi sulla difficile Coss.

Il Gymnasium di Basilea, una scuola in latino, era in uno stato penoso. Agli studenti veniva insegnato il latino e una selezione dei classici antichi. Il greco era facoltativo.

Gli insegnanti non se la prendevano troppo e in piena classe scoppiavano scontri fisici. Come la maggior parte dei genitori, anche gli Euler assunsero un tutore, in questo caso un giovane teologo che si chiamava Johann Burckhardt il quale, nelle dispute con i geometri ed i filosofi inglesi della natura, specialmente con Brook Taylor, parteggiava per Johann I Bernoulli.

Johann I Bernoulli

Burckhardt insegnò ad Euler le materie umanistiche e la Matematica, materia in precedenza eliminata dal curriculum con un voto popolare.
Nel 1720, Euler si iscrisse alla facoltà di Filosofia dell'Università di Basilea, la scuola di base delle arti e delle scienze. Aveva tredici anni, l'età normale in quel periodo per iscriversi all'Università. L'Università era in declino. Le iscrizioni degli studenti erano calate da più di mille un secolo prima a poco più di cento. Aveva soltanto diciannove professori, sottopagati e per la maggior parte mediocri. L'eccezione era Johann I Bernoulli. La facoltà di Filosofia forniva l'educazione preliminare necessaria alla scelta di una specializzazione di grado superiore. Grazie al lavoro e ad una potente memoria, Euler padroneggiò tutte le materie.
A quattordici anni Euler fece una prolusione dal titolo "Declamatio: De Arithmetica et Geometria", vantando la superiorità della Geometria. Dopo un discorso in latino che lodava la temperanza, nel 1722 ottenne la prima laurea. Nell'autunno del 1723 completò gli esami di Maestro d'arte. Nel giugno del 1724, il diciassettenne Euler ottenne ufficialmente il titolo dopo una conferenza pubblica in latino sul suo argomento di tesi, un confronto fra la filosofia naturale di René Descartes e quella di Isaac Newton, insieme alle conseguenze di ciascuna di esse.
Nell'ottobre del 1723, il padre di Leonhard gli chiese di iscriversi a teologia, per prepararsi a diventare pastore. Avrebbe soprattutto dovuto studiare greco, ebraico, teologia protestante e lettere classiche. Circa in questo periodo, cominciò ad esibire la sua memoria fotografica, recitando a memoria lunghi passi dell'Eneide di Virgilio o addirittura tutto il testo. Era in grado di citare il primo e l'ultimo verso di ogni pagina della sua copia.

Ancora a settant'anni ricordava per intero l'Eneide. Il curriculum di teologia gli permetteva di studiare Matematica. Egli aveva già cominciato a farsi seguire da Bernoulli e, passando la maggior parte del tempo sulla Matematica, fece pochi progressi nelle altre materie. All'Università, Euler era diventato amico di Johann II Bernoulli che probabilmente lo aiutò nella sua richiesta di lezioni private. Il maggiore dei Bernoulli le offriva agli altri studenti, ma le rifiutò ad Euler. Piuttosto consigliò il giovane studioso di leggere con diligenza alcuni difficili libri di Matematica, Astronomia e Fisica finché non avesse trovato degli ostacoli. I due si sarebbero incontrati il sabato pomeriggio e Bernoulli avrebbe mostrato ad Euler come superare gli impedimenti ed ottenere la via verso la soluzione. Euler dedicò tutti i suoi sforzi per ridurre al minimo i problemi. Quando Bernoulli gli mostrava come superare una difficoltà, egli rimaneva incantato dal fatto che ne svanisse un'altra decina. Bernoulli stava scoprendo il genio del suo studente. L'autobiografia di Euler dice che leggere i capolavori seguito da un insegnante capace "è il miglior metodo per il successo negli argomenti matematici". O almeno era così per uno studente tanto dotato. Fu probabilmente verso il 1725 che il maggiore dei Bernoulli, ormai intorno alla sessantina, si recò a Riehen per convincere il suo vecchio compagno Paul a far trasferire il figlio a matematica.
Nel 1725 il giovane Euler cercava un impiego. Producendo più laureati di quanti ne occorressero, la Svizzera doveva esportarli. Nel 1725, gli amici di Euler, Daniel e Nicholas II Bernoulli accettarono un posto alla nuova Accademia delle Scienze di San Pietroburgo. Dopo l'improvvisa morte di Nicholas II, nell'autunno del 1726, Euler fu invitato a raggiungere l'Accademia per occuparsi di Medicina, con uno stipendio di 200 rubli, che egli considerava non sufficiente. Nonostante ciò, decise di recarvisi non appena il tempo fosse migliorato. Nel frattempo si iscrisse a corsi di anatomia e di fisiologia. Quando a Basilea morì il professore di Fisica, il maggiore dei Bernoulli raccomandò ad Euler di far domanda per ricoprire il posto. Il saggio che egli sottopose come campione era un articolo di acustica, di sedici pagine, intitolato "De sono", che gli storici descrivono come sua dissertazione. è divenuto un classico. Ma l'Università fece una selezione a sorte ed il giovane Euler non entrò in finale. Il 5 aprile 1727, tre giorni dopo che Benedict Stähelin era diventato professore di Fisica, Euler lasciava Basilea per sempre. Aveva ormai raggiunto una certa reputazione. Quell'anno, il suo saggio sull'alberatura delle navi, sottoposto al premio annuale dell'Accademia di Parigi, aveva ottenuto un accessit o menzione onorevole, sebbene egli potesse osservare solo barche sul Reno e non navi sull'oceano.

Nel Colosso del Nord: il fondamento della ricerca di Eulero

Dopo aver disceso il fiume Reno fino a Francoforte, quindi via terra verso il nord, attraverso Amburgo e Lubecca, e dopo un duro viaggio lungo la costa della baia di Lubecca e del mar Baltico, Euler arrivò a Pietroburgo nel maggio del 1727, due mesi dopo la morte di Isaac Newton, per cominciare la propria illustre carriera. Fu probabilmente grazie all'intervento di Jakob Hermann, di Daniel Bernoulli e di Christian Goldbach che Euler fu sistemato nella divisione matematica, anziché quella medica, della nuova e dinamica Accademia delle Scienze. Ma c'era uno stato di costernazione.

La sua benefattrice, l'imperatrice Caterina I, vedova e successore di Pietro I, era morta da una settimana. I nobili del nuovo governo vedevano l'Accademia come un'intrusione straniera e congelarono i finanziamenti; Euler dovette accettare un posto di medico della marina russa, che stava diventando la potenza maggiore del Baltico. Era al servizio dell'ammiraglio de Sievers. Le fortune dell'Accademia migliorarono con la nomina dell'imperatrice Anna di Courland nel 1730.

Quando Hermann e Georg Bilfinger se ne andarono, Daniel Bernoulli succedette a Hermann nella prestigiosa posizione di professore di matematica. Euler declinò l'offerta di promozione da parte della marina russa e tornò a tempo pieno all'Accademia, sostituendo Bilfinger come professore di fisica. Fino al 1733 risiedette nella casa di Bernoulli ed i due spesso cenavano insieme, parlando occasionalmente di argomenti scientifici. Fra gli argomenti su cui collaboravano c'era la Hydrodynamica di Bernoulli, che comparirà nel 1738.
Quando Daniel Bernoulli tornò a Basilea, nel 1733, Euler gli succedette. Con una situazione finanziaria migliore, nel gennaio del 1734 si sposò con Katharina Gsell, figlia dell'artista Georg Gsell, originario di St. Gall in Svizzera, e comprò una casa di legno sull'isola Vasilevskij. Il 27 novembre nacque il loro primo figlio, Johann Albrecht, così chiamato in onore del presidente dell'Accademia, barone Johann Albrecht de Korff. Christian Goldbach fu il padrino.

Si trattava di importanti alleati. Gli Euler avranno in totale tredici figli, ma solo tre maschi e due femmine sopravviveranno alla prima infanzia. Katharina organizzava e gestiva tutta la casa, lasciando al marito più tempo per studiare e scrivere.All'Accademia, il cordiale Euler aveva rapporti tesi con il suo dispotico e crudo amministratore, Johann Schumacher, amico di suo suocero, di cui frequentava la casa. A San Pietroburgo Euler continua le ricerche fondamentali, variabili in un vasto spettro scientifico, dalla teoria dei numeri e la teoria musicale all'astronomia e la balistica.

Nei suoi Commentarii, l'accento è posto sull'analisi infinitesimale e sulla meccanica razionale. In teoria dei numeri, Goldbach era la maggior fonte di stimolo, proponendo problemi di difficile soluzione che risulteranno fra i primi risultati di Euler. In una lettera del dicembre 1729, Goldbach chiede se è vera la congettura di Fermat per cui tutti gli interi della forma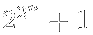      

sono primi. Euler lo conferma per n=1; 2; 3 e 4, ma nel 1732 mostra che n=5 è un controesempio. Infatti 232+1= 4.294.967.297=641 x 6.700.417.
Aveva scoperto che i numeri di Fermat composti devono avere divisori della forma 2n+1k + 1. Da qui era stato facile risalire al divisore 641, il caso in cui k=10 fornisce 26(10)+1. Nel 1734 Euler scopre una affascinante relazione fra i logaritmi naturali e la serie armonica. Questo rende possibile il calcolo della costante di Euler o costante "gamma", che è

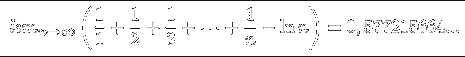
"Gamma" è una delle importanti costanti reali che appaiono in analisi, insieme ai numeri trascendenti π ed e. Attualmente non è noto se "gamma" è razionale, algebrica o trascendente. Nel ventesimo secolo, Hardy promise di rinunciare alla propria cattedra Saviliana di Oxford a vantaggio di chiunque avesse dimostrato che "gamma" è algebrica.
Nel corso degli anni '30 Euler comincia a preparare la sua Introductio in analysin infinitorum [E101, E102] del 1748, completando massicci calcoli, mettendo a punto metodi computazionali e sviluppando le tre classi di funzioni trascendenti dell'Analisi infinitesimale - esponenziale, logaritmica e trigonometrica. Seguendo Leibniz e Bernoulli, egli divide le funzioni in due classi: algebriche e trascendenti. Fu probabilmente Johann I Bernoulli a introdurlo alla funzione esponenziale ex, in cui l'esponente è variabile. Euler usa il simbolo e per la prima volta in un articolo pubblicato postumo sull'artiglieria, scritto nel 1728 o nel tardo 1727 [E853]. Newton e Bernoulli l'avevano definito, in maniera indipendente, come limite dello sviluppo di (1+1/n)n al tendere di n all'infinito.
Utilizzando la serie:

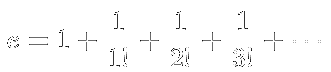
data qui nella moderna notazione fattoriale, in seguito Euler calcola il suo valore in 2,718281828 esatto fino alla nona cifra decimale. Nel 1737 calcola e come frazione continua[6].

In trigonometria trasforma le corde tolemaiche e le semi corde in rapporti numerici, facendo diventare funzioni le curve trigonometriche. Probabilmente dopo la lettura del precorritore lavoro di Roger Cotes ed Abraham de Moivre Miscellanea analytica del 1730, nel 1737 scopre che (cos z + √-1 sin z)n= cos nz + √-1 sin nz o, nella sua successiva notazione eix = (cos x + i sin x), la formula fondamentale della trigonometria analitica. I suoi massicci calcoli cominciano a dare maggior peso ai logaritmi nell'analisi infinitesimale, ma egli non ha ancora stabilito e come base naturale per essi o impiegato in maniera sistematica i per rappresentare √-1.
Nel 1736, il sindaco di Danzica chiede ad Euler di risolvere un problema di carattere ricreativo. Il centro della città di Königsberg, nella Prussia dell'est, è un'isola circondata dal fiume Pregel. Sette ponti attraversano il fiume. Il problema riguarda la possibilità per un viaggiatore di percorrere i ponti con un cammino connesso che passi solo una volta su ciascun ponte, per tornare al punto di partenza. Euler trovò facile il problema e lo risolvette con il solo ragionamento. Collegando il numero di ponti con il numero di volte in cui il viaggiatore entra in una regione, egli mostrò che sotto le date condizioni il cammino non è possibile. La sua memoria "Solutio problematis ad geometriam situs pertinentis" [E53], contenente la soluzione, è il primo contributo al campo che si svilupperà come geometria situs o analusis situs, cioè topologia. Anche se nella memoria non appare nessun grafo, è considerata il contributo iniziale alla teoria dei grafi.
Uno dei motivi principali perché alla fine degli anni '30 Euler cominciasse ad essere riconosciuto come il massimo matematico d'Europa è la soluzione del problema di Basilea, ottenuata nel 1734/35: la somma esatta della serie infinita degli inversi dei quadrati, il cui valore oggi si denota:

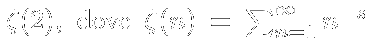
Per più di settantacinque anni i geometri avevano cercato la somma di questa serie lentamente convergente.

Il Methodus differentialis di James Stirling del 1730 fornisce la migliore approssimazione del tempo, precisa fino all'ottava cifra decimale: 1,644034066. Calcolandola in quattro maniere diverse, Euler arrivò inaspettatamente alla somma esatta π2/6. Nel dicembre del 1734 presentò le proprie scoperte all'Accademia di San Pietroburgo. La funzione zeta fu collegata da Euler con la distribuzione dei numeri primi ed in una memoria del 1737 egli introdusse la sua celebre formula di scomposizione: se P è l'insieme dei primi:

La moltiplicazione a destra fornisce 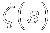 . Il caso s = 1 è la serie armonica, che diverge. Poiché il prodotto corrispondente deve avere infiniti fattori, Euler aveva indirettamente dimostrato che i primi sono infiniti.
Ancora più importante, per la crescente reputazione di Euler durante gli anni `30, è la pubblicazione della sua Mechanica [E15,E16], 890 pagine in due volumi, come supplemento ai Commentarii nel 1736[7]. Il lavoro rompeva decisamente con le forme geometriche della meccanica ed introduceva le equazioni differenziali di quelli che sono oggi detti punti materiali. Con l'eccezione di Benjamin Robins in Inghilterra, che criticò il suo uso sistematico delle equazioni differenziali, i geometri ed i filosofi naturali di tutta Europa, incluso Johann I Bernoulli, salutarono il lavoro come una pietra miliare della Fisica. La sua recensione nelle Mémoires de Trevoux parigina concludeva dicendo che Euler aveva creato la meccanica moderna. Nella sua Mécanique analytique del 1788, Joseph Louis Lagrange dice che la Mechanica è "la prima grande opera in cui l'analisi viene applicata alla scienza del moto". Ma è sbagliato presentare la Mechanica semplicemente come una traduzione nell'Analisi infinitesimale di molta parte dei Principia mathematica di Newton. La Mechanica è il primo grande lavoro di Euler nel suo ambizioso programma di risolvere analiticamente il moto dei corpi che sono elastici, fluidi, flessibili e rigidi - un compito che da solo avrebbe esaurito le forze della maggior parte dei geni scientifici e che egli completò come parte del suo programma di ricerca dei successivi vent'anni.
L'Accademia assegnava ad Euler molti compiti. Fu membro della commissione pesi e misure, cooperò al collaudo di pompe da fuoco, seghe e scale. Stimolato dalle ruote ad acqua di Johannes Andreas Segner cominciò a sviluppare macchine idrauliche. La sua attività si estendeva perfino ad ordinare carta e inchiostro per la stampa dell'Accademia. Contribuì in maniera decisiva ad un progetto statale dell'Accademia, la seconda Spedizione della Kamcatka (o del Grande Nord) che durò dal 1734 al 1743. Bisognava preparare la prima accurata mappa dell'impero russo e delle sue regioni, determinando astronomicamente longitudine e latitudine e facendo migliori misure geodetiche. Fu il progetto più finanziato della prima Accademia. Euler continuò ad aiutare l'astronomo francese Joseph-Nicolas Delisle e, dal 1735, diresse la sezione geografica dell'Accademia. Calcolò le efemeridi e, nel 1737, fornì istruzioni uniformi agli esperti di geodesia della spedizione, specialmente allo studioso russo Vasilij Tatysev, che stava studiando le possibilità economiche degli alti Urali. Euler incoraggiò Gerhard Müller a raccogliere gli archivi delle spedizioni come sorgenti primarie di una futura storia della Siberia.

Fra le controversie e le rivalità che abbondarono durante l'Illuminismo, i sostenitori di Cartesio, inizialmente su posizione dominante, discutevano con quelli di Newton all'Accademia delle Scienze di Parigi su quale scienza fosse superiore, mentre nelle università tedesche ed a San Pietroburgo, i sostenitori di Leibniz e di Wolff si opponevano alla scienza di Newton. Euler sintetizzò in modo selettivo gli elementi consistenti dei primi tre, aggiunse le proprie idee e respinse la Metafisica di Wolff.

I sostenitori di Cartesio e quelli di Newton dissentivano sulla forma della Terra. La sua determinazione era un elemento cruciale per indicare la superiorità di una scienza rispetto all'altra. La disputa scientifica, insieme ad un impeto della cartografia francese ed al desiderio di verificare alcuni strumenti, spinsero la monarchia francese e l'Accademia di Parigi a mandare delle spedizioni in Perù, dal 1735 al 1744, e in Lapponia, dal 1736 al 1737, per misurare un arco di meridiano e quindi dedurre la vera forma del pianeta. (Pierre) Louis Moreau de Maupertuis (1698-1759), che diresse la spedizione in Lapponia, al ritorno affermò che le sue scoperte mostravano che aveva ragione Newton. Euler lodò i dati di Maupertuis, ma non li trovò determinanti. Aspettava i dati della spedizione in Perù. Nel 1738, nell'ipotesi che la densità interna della terra fosse variabile, non omogenea, Euler ne calcolò correttamente la forma, come meno appiattita ai poli rispetto a quella di Newton. La terra è più un'arancia che un melone. Euler affermò di accettare ancora la legge di attrazione di Newton, ma pensava che avesse bisogno di una leggera modifica.
La reputazione di Euler crebbe notevolmente anche con la vittoria del prestigioso Prix de Paris, il premio annuale dell'Accademia di Parigi, tre anni di seguito a partire dal 1738. Ai concorsi di questo massimo riconoscimento scientifico egli sottoporrà diciotto lavori. L'aver ricevuto il premio dodici volte, più una con il nome di Johann Albrecht, il suo figlio maggiore, è un fatto ancora insuperato. Il suo principale rivale, Daniel Bernoulli, ha vinto dieci volte. Il premio di Parigi veniva conferito ad anni alterni in materie teoriche o applicate. Euler ha vinto in entrambe le categorie, cinque volte con articoli pratici sulla navigazione e la costruzione delle imbarcazioni.

Pur in possesso di un'attitudine diffidente, il geniale Euler si arrabbiava raramente e tendeva ad evitare le dispute a San Pietroburgo, lavorando al riparo dell'Accademia. Divenne critico nei confronti della Filosofia e della scienza dei seguaci di Wolff, influenti nell'Europa di lingua tedesca. Euler li respinse avendo trovato alcuni errori matematici nei libri di Wolff, incluso la Cosmologia generalis del 1731 e criticò l'esistenza di monadi animate come sostanze elementari del mondo fisico. Per un po' mantenne le critiche in un ambito ristretto, volendo precisare le sue idee con ulteriori ricerche prima di presentarle al vasto pubblico.

Con l'eccezione di due seri problemi di salute, della morte di tre figlie ancora piccole e dell'alloggiamento di soldati in casa, nonostante la sua strenua opposizione, la vita di Euler negli anni '30 era stata poco disturbata. Di tanto in tanto soffriva di febbri pericolose. Nel 1735, febbre, mal di testa e tempo rigido indebolirono la sua salute. Non aveva ancora problemi alla vista, che arrivarono nell'estate del 1738, quando una febbre quasi mortale ed un'infezione gli provocarono un ascesso all'occhio destro. Secondo Fuss, la cui informazione proviene da Euler quando era ormai vecchio, egli aveva perso completamente la vista dall'occhio destro ed era sulla strada della totale cecità. Ma i ritratti di Euler e la corrispondenza del tempo suggeriscono un graduale indebolimento della vista nell'occhio destro, con occasionali remissioni parziali.
Verso l'estate del 1740, la famiglia Euler sembrava ben sistemata a San Pietroburgo. Nel mezzo dei problemi di salute di Euler, Federico II, che all'età di ventotto anni era asceso al trono di Prussia alla fine di maggio, lo invitò a prendere parte alla rinnovata Società Reale delle Scienze di Brandenburgo. Euler non trovò sufficiente la prima offerta e chiese lo stesso salario che riceveva a San Pietroburgo. Ma l'idea di lasciare la Russia imperiale lo attraeva. Dopo la morte dell'imperatrice Anna, avvenuta nel 1740, la vita nella capitale della Russia era diventata pericolosa, soprattutto per gli stranieri. Nel febbraio del 1741, Euler si recò dal nuovo ambasciatore prussiano, barone Axel von Mardefeld, e seppe che Federico aveva accolto la sua proposta di salario. Accettò l'offerta, ma non gli fu possibile lasciare San Pietroburgo prima di giugno. Quando il suo vecchio maestro, il settantatreenne Johann I Bernoulli, seppe del trasferimento di Euler a Berlino, gli mandò una lettera, in settembre, nella speranza che tornasse nella città natale a trovare i genitori: il più ardente desiderio di Bernoulli era di avere la possibilità di vedere ancora una volta Euler, prima di morire.[8].

Nella Berlino di Federico II: all'apice della carriera 

Il 25 luglio 1741, dopo un duro viaggio di quattro settimane lungo il mar Baltico, con una breve sosta a Stettino, la famiglia Euler arriva a Berlino. Nell'ottobre del 1742, Euler scrive a Goldbach di aver comprato una bella casa con un vasto giardino. Per i prossimi 23 anni, risiederà al 21 di Behrenstrasse. Nel 1746, la famiglia era ormai di sette persone. A Johann Albrecht e Karl Johann si erano aggiunti Katharina Helene, nata nel 1741, Cristoph, nel 1743 e Charlotte l'anno successivo. Tutti sopravvissuti, anche se la famiglia dovette soffrire per l'alta mortalità infantile del tempo. Un figlio nato nel 1747, due gemelle due anni più tardi ed un altro figlio nel 1750 morirono prima di compiere un anno.
Eulero amava portare i figli allo zoo e guardare i giochi dei cuccioli d'orso. Prima di dormire spesso leggeva ai figli le Scritture. Ormai Euler fumava la pipa: le sue lettere al teologo di Basilea Johann Kaspar Wettstein-Sarasin, cappellano della duchessa del Galles, sono piene di richieste del suo amato "buon tabacco" inglese, che gli veniva spediato via Amsterdam. Euler aveva pochi divertimenti. Il maggiore era suonare il piano, ed egli invitava a casa compositori per eseguire i lavori recenti. A Berlino era diventato un bravo giocatore di scacchi. A casa sua si raccoglieva una piccola cerchia di colleghi. Fino al 1756 vi si recavano gli studenti russi, mandati dall'Accademia di San Pietroburgo per essere assistiti da Euler. Nei giorni feriali, dalle 10 alle 11 egli insegnava loro e ad altri giovani nobili, Matematica, Astronomia e Fisica.

Nel gennaio del 1744, Federico, come parte della rituale celebrazione del suo trenteduesimo compleanno, fondò formalmente l'Accademia, consistente di quattro piccole classi, con i loro direttori eletti a vita. Le classi erano Filosofia sperimentale, un termine grosso modo equivalente a Fisica, Matematica, Filosofia speculativa e Letteratura (con Filologia). Quattro curatori, scelti fra i nobili vicini al sovrano, avrebbero affiancato i direttori nella gestione dell'Accademia.

Il 1746 fu importante per la storia dell'Accademia. Federico accettò che Maupertuis progettasse una costituzione basata su quella dell'Accademia di Parigi. Dopo la sua messa a punto, il re, in giugno, confermò Maupertuis presidente perpetuo con poteri autocratici, e i membri elessero Euler direttore a vita della classe matematica. Erano occorsi cinque anni ad Euler per ottenere la posizione prevista dall'invito.
L'Accademia aveva un premio annuale. L'argomento del 1746 era la causa dei venti. Euler presiedeva la commissione che scelse il vincitore, il famoso Jean d'Alembert, per un articolo astratto contenente nuove equazioni differenziali. Un altro concorrente, Daniel Bernoulli, trovò che il lavoro di d'Alembert era debole: fra Euler e Bernoulli, il suo migliore amico, si stava sviluppando qualche tensione.
Euler aveva molti compiti all'Accademia. Il suo primo incarico fu quello di sovrintendere la costruzione dell'osservatorio e poi del suo funzionamento. Il nuovo edificio dell'Accademia non fu pronto prima del 1752. Come membro del direttorio dell'Accademia, Eulero era a capo del comitato editoriale che sceglieva gli articoli per le Mémoires della sua rivista, inoltre dirigeva la biblioteca. Egli, insieme al segretario dell'Accademia, Samuel Formey, fungeva da intermediario fra il francese Maupertuis ed i membri di lingua tedesca.
Maupertuis non godeva di buona salute. Nel 1750 dovette assentarsi sempre più spesso e per periodi sempre più lunghi. Durante la sua assenza, Euler fungeva da presidente effettivo dell'Accademia. Tutto ciò non lo sovraccaricava: preparava anche almanacchi e varie mappe geografiche per finanziare l'Accademia e si prendeva cura del giardino botanico, ordinando personalmente piante ed alberi.

Dal 1746 al 1748, Euler ricevette l'offerta di posizioni con maggiore prestigio scientifico, fuori Berlino. Avendo perso numerosi membri, l'Accademia di San Pietroburgo lo invitò a tornare nel 1746, ma in giugno egli declinò l'offerta. L'anno successivo, Schumacher gli chiese di rivedere un articolo sul calore del chimico, fisico e poeta russo Michail Lomonosov.

Poiché Lomonosov aveva studiato con Wolff e tradotto in russo il suo testo di Fisica, Schumacher si aspettava una relazione sfavorevole da parte di Euler, ormai dichiarato oppositore di Wolff. Con sua grande sorpresa, Euler apprezzò il lavoro di Lomonosov. Il suo sostegno a questo russo di talento sarebbe continuato in seguito. Nel giugno del 1746 scrisse a Wettstein che desiderava diventare fellow della Royal Society di Londra. Le sue Philosopical Transactions continuavano ad essere essenziali per il suo lavoro ed egli seguiva da vicino le osservazioni degli astronomi inglesi, particolarmente di James Bradley, che aveva scoperto un'aberrazione della luce stellare nel 1729 e che era vicino a stabilire la mutazione o leggera oscillazione dell'asse terrestre. I rivali di Euler, Daniel Bernoulli e Alexis Clairaut ne erano già diventati membri. A quel tempo i candidati dovevano sottoporre una domanda per diventare membri, ma Euler si rifiutò: Wettstein decise ugualmente di nominarlo ed egli fu eletto nel 1747.
Nel gennaio del 1748, morì Johann I Bernoulli e l'Università di Basilea offì la cattedra ad Euler, che non rispose mai. Egli decise di rimanere al largo, ritenendo che il posto dovesse andare a Daniel Bernoulli.
Nonostante i crescenti elogi, il plebeo e repubblicano Euler non era popolare presso la corte reale prussiana. La società prussiana del diciottesimo secolo era aristocratica. I rapporti di Euler con Federico II erano complicati. Sebbene impressionato dai suoi risultati, il re ed i nobili lo consideravonbo privo di maniere gentili - la stessa accusa che era stata sollevata contro Galileo[9]. Il re dubitava che fosse edificante conversare con Euler, anche se Euler sembrava amare la conversazione, metteva le persone a proprio agio, aveva senso di humor ed era un grande narratore. Un lettore prodigioso, con buona conoscenza anche dei classici.
A Berlino, fra il 1741 ed il 1766, Euler scrisse o completò più di 380 fra memorie e libri. La loro combinazione di profondità, originalità, ampiezza e numero assoluto è inarrivabile nella storia della Matematica. Mentre continuava a insistere sull'analisi dell'infinito e sulla Meccanica razionale, estese l'ambito delle proprie ricerche all'Astronomia, all'Ottica ed alla balistica. Cominciò a studiare anche l'elettricità ed il magnetismo. Relativamente privo di progetti statali durante i primi anni a Berlino, Euler si immerse in vaste e profonde ricerche.
Il primo dei fondamentali libri pubblicati da Euler negli anni '40 fu il suo Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes... [E65], completato a San Pietroburgo nel 1741. Il Methodus inveniendi presenta lo stadio iniziale del calcolo delle variazioni, dedicato a trovare le lunghezze massimali e minimali, se esistono, delle curve piane nel corso del loro movimento e gli estremi fra i valori degli integrali. Su richiesta di Daniel Bernoulli, Euler aggiunse due appendici. La prima, un iniziale trattato generale sulla teoria matematica dell'elasticità, comprende il problema della membrana vibrante e la formula di Euler sulla resistenza per determinare il carico critico e decidere la forza delle colonne. La seconda appendice contiene una forma generale del principio di minima azione. Secondo il suo editor del ventesimo secolo, Constantin Carathéodory, il Methodus inveniendi è "uno dei più bei lavori matematici mai scritti".[10]
Pur completando il Methodus inveniendi, Euler rimase attivo in teoria dei numeri, ottenendo nel 1741 la prima di tre dimostrazioni del piccolo teorema di Fermat. In simboli moderni: ap-1≡(mod p) se p è primo ed a è relativamente primo con p. Euler inaugurò una campagna di sette anni per dimostrare tutte le congetture di Fermat sulle somme di quadrati.
Nel 1742 e 1743 Euler proseguì in una seconda fase di intensi calcoli di analisi infinitesimale, in preparazione della sua Introductio. Escogitò tecniche migliori per sommare le funzioni zeta per ogni intero minore di 26. Utilizzando gli sviluppi di Taylor, abili sostituzioni ed altre tecniche, Euler sommò serie infinite, specialmente per π ed e, per la maggior parte con più precisione rispetto ad ogni predecessore. Le frazioni continue, ad esempio, fornirono e=2,718281845904... Euler aveva studiato in precedenza la formula di de Moivre (cos x+isen x)n=cos nx+isen nx, anche se non ancora utilizzando i, ed ora ritornò ad essa, rafforzando la connessione fra le usuali funzioni trigonometriche e quelle esponenziale e logaritmica, estendendo il loro dominio ai numeri complessi. Prima del 1744 aveva ottenuto l'equazione eix=cos x + isen x, da cui segue eiπ=-1[11]. Poiché Euler definiva il logaritmo naturale come l'inverso della funzione esponenziale, ciò significava che ln(-1)=iπ;. Quindi il logaritmo di un numero negativo è un numero immaginario. Subito Euler e d'Alembert cominciarono a discutere sulla natura dei logarirmi dei numeri negativi[12]. Si ritiene che lo studio che inizia con la formula di de Moivre sia il lavoro conclusivo di Euler sulla Introductio.

Dopo il suo esordio nel 1746, la nuova Accademia ebbe una profonda spaccatura sull'argomento del premio del 1747, la dottrina delle monadi. La questione mise Euler in contrasto con i filosofi wolffiani, che erano molto influenti nelle università tedesche. La dottrina delle monadi era centrale per la metafisica di Leibniz e quella di Wolff. Leibniz aveva proposto le monadi - animate, elastiche, immateriali, punti geometrici di energia - come i più piccoli componenti della materia. Wolff le ridefinì energie ed in generale atomi indivisibili.

Gli accademici non erano previsti come partecipanti alla competizione annuale, ma Euler ruppe la regola attaccando anonimamente la dottrina con il pamphlet: Gedancken von den Elementen der Cörper... (Pensieri sugli elementi dei corpi...) [E81]. Alle molecole, come Euler le chiamava, associava come proprietà fondamentale l'impenetrabilità, richiamandosi a Newton, e l'infinita divisibilità, un concetto probabilmente preso da Euclide e da Leibniz. Egli sosteneva che le leggi della fisica non possono verificare empiricamente o quantificare le monadi.
Fino ad ora Wolff, che era all'autunno della propria carriera, aveva espresso ammirazione per le ricerche scientifiche di Euler. Ma questo trattato lo fece infuriare e nel novembre del 1746 scrisse per lamentarsi al presidente dell'Accademia, Maupertuis, che non aveva seguito la questione dall'inizio perché non leggeva il tedesco. I filosofi wolffiani si unirono all'attacco nei confronti di Euler e la controversia rivelò uno spaccamento istituzionale fra l'Accademia e le Università negli stati della Germania del nord. Su richiesta di Maupertuis, Samuel Formey, lo storiografo e futuro segretario dell'Accademia, tradusse gli articoli dal tedesco al francese. Sebbene si dichiarasse neutrale, Formey divenne il principale oppositore di Euler.

Anche se Daniel Bernoulli lo pregò di non immischiarsi in questo dibattito metafisico, nel 1747, Euler estese il proprio argomento ad un esercizio di Fisicoteologia. Affermò che la dottrina delle monadi di Leibniz ed il principio di armonia prestabilita fra mente e corpo contraddicono la tradizionale concezione cristiana di peccato originale. Quell'anno Johann Justi vinse il premio dell'Accademia di Berlino con un modesto articolo di critica al concetto di monade.
La battaglia di Euler con i liberi pensatori wolffiani era solo all'inizio. Con il suo stringente metodo razionale, Wolff aveva dato al principio di ragion sufficiente uno statuto minore che al principio di contraddizione, in contrasto con Leibniz e Johann I Bernoulli. Euler biasimò l'uso di Wolff del principio di ragion sufficiente. La contesa si estese alla Matematica. Nel suo sviluppo dell'Analisi infinitesimale, Euler sovrastava di gran lunga Wolff, che sosteneva il primato della Geometria. Era in corso di stampa il libro di Euler Introductio in analysin infinitorum, probabilmente il testo più influente della matematica moderna, che sarebbe apparso nel 1748.
Nel frattempo, Euler stava facendo importanti progressi in Ottica, Meccanica e sul trattamento di tempo e spazio. Anche la cartografia e l'esplorazione continuavano ad attrarre l'attenzione di Eulero. In una lettera a Wettstein-Sarasin in Inghilterra, apparsa sulle Philosophical Transactions della Royal Society del 1747 [E107], commenta la ricerca russa di un passaggio diretto, a nord ovest, attraverso l'America, che fornisse una connessione marittima fra la baia du Hudson e l'oceano Pacifico. Euler chiamava "impresa gloriosa" la ricerca in corso. Il capitano Vitus Bering, che aveva condotto la seconda spedizione russa in Kamcatka nel nord est della Siberia ed era morto nel 1741, sospettava che le terre a nord della Siberia fossero collegate alla California, e quindi che non ci fosse un passaggio per via d'acqua. Euler temeva che Bering avesse ragione, ma aspettava i risultati delle esplorazioni.

Nel 1748, soltanto settancinque anni dopo la sua nascita, il Calculus era a mala pena uscito dalla propria infanzia, privo di un quadro generale che identificasse e disponesse sistematicamente i concetti fondamentali con un programma di sviluppo della materia.
Dopo Leibniz, i geometri continentali avevano sviluppato una teoria delle funzioni. Presentandole come oggetti autonomi, centrali per il Calculs, il primo volume della Introductio costruisce una teoria metodica ed esauriente delle funzioni algebriche e trascendenti. La definizione di funzione stava evolvendo. Il libro II della Introductio unifica il cartesiano con l'analitico e li mette per la prima volta in forma moderna. Nel 1748 Euler completò anche il manoscritto delle Instutiones calculi differentialis [E212] anche se gli occorsero sette anni per pubblicarlo.
Nel 1749 viene pubblicata la Scientia navalis di Euler, sulla costruzione e propulsione delle navi. Fornisce ottimi progetti di navi, che prendono in considerazione la stabilità, la manovrabilità e la velocità, opposte le une alle altre. Eccellente sia per la Matematica applicata che per quella teorica, la Scientia navalis prosegue il programma di Euler sulla fondazione della Meccanica dei continui.
Già prima del 1750 Euler, che aveva l'abitudine di introdurre gli argomenti da sviluppare in seguito, si indirizzò verso quella che alla fine del diciannovesimo secolo diventerà la topologia combinatoria. Egli fornì una elaborata ma imprecisa dimostrazione in geometria solida della formula v+f=e+2, che lega in un poliedro convesso il numero v dei vertici, e dei lati e f delle facce. La forma moderna v-e+f=2 definisce la caratteristica di Euler.
Nei tardi anni `40 la rivalità fra d'Alembert, Daniel Bernoulli, Clairaut ed Euler si intensificò. La competizione non era necessariamente di uno nei confronti degli altri.
Bernoulli, ad esempio, si opponeva più fortemente a d'Alembert di Euler, ed egli, Clairaut ed Euler avevano occasionalmente d'Alembert come comune oppositore.

In Matematica pura, Euler e d'Alembert rimasero in corrispondenza dal 1746 al 1751 soprattutto sui logaritmi dei numeri negativi, che entrambi ritenevano pieni di paradossi[13], e le radici immaginarie delle equazioni algebriche. Il tono delle lettere di d'Alembert suggerisce il tentativo di stupire Euler insieme ad uno sforzo di autopromozione.
Dopo che Euler, in una lettera del dicembre 1746, aveva respinto con tatto l'idea di d'Alembert che log(-x)=log x per i numeri positivi x, nel gennaio del 1747 d'Alembert risponde che la nuova informazione lo disturbava e pregava Euler di eliminare una parte del suo trattato intitolato "Recherches sur le calcul integral", spedito l'anno precedente alle Mémoires dell'Accademia di Berlino, in cui discuteva log (-x). La controversia sul logaritmo continuò[14].
Ma ciò che condusse soprattutto i due alla rottura non fu la competizione in Matematica pura ma in Fluidodinamica. Nel 1749 d'Alembert sottopose uno goffo articolo, Essai d'un nouvelle théorie de la résistence des fluids, al premio dell'Accademia di Berlino. Egli introduceva il concetto di pressione del fluido e deduceva alcune corrette equazioni alle derivate parziali sul flusso simmetrico, piano e rotazionale, ma con un certo timore le cuciva in un tessuto di congetture ed errori. Sebbene la giuria, presieduta da Euler, lo considerasse l'articolo migliore, Euler ritenne che il premio non fosse giustificato. Nel 1750 e 1751, Euler preparò alcuni articoli di Fluidodinamica che semplificavano e generalizzavano le teorie idrauliche di Johann I e Daniel Bernoulli, portando l'argomento alla sua forma definitiva. Senza citarne l'origine, egli si basava sul concetto di pressione di d'Alembert e sulle sue equazioni differenziali. Nel settembre del 1751 d'Alembert spedì ad Euler una lettera bellicosa, rompendo con lui e criticandolo nella voce "Hydrodynamique" del volume 8 della Encyclopédie.
Alla svolta degli anni `50, Clairaut, d'Alembert ed Euler si contendevano la supremazia nel tentativo di risolvere il problema dei tre corpi o problema delle perturbazioni. In Meccanica celeste, la grande questione irrisolta era se l'attrazione newtoniana da sola potesse descrivere tutti i moti celesti.
Dal 1742 Euler, che stava preparando le tabelle lunari, esortava a compilare maggiori osservazioni telescopiche. Sebbene accettasse la legge dell'inverso del quadrato, voleva indagare se desse solo una buona approssimazione a qualche moto celeste, e quindi richiedesse una piccola correzione per la precisione degli oggetti poco distanti l'uno dall'altro all'interno del nostro sistema solare, come ad esempio la Terra e la Luna, oppure Saturno e Giove in congiunzione, trascurabile a distanze maggiori. Dopo aver osservato nel 1743 che Newton non aveva spiegato completamente il movimento dell'apogeo lunare, la maggior distanza dalla Terra, Clairaut cominciò a riesaminarlo. All'Accademia di Parigi nel 1747 annunciò che le sue equazioni differenziali e le approssimazioni del primo ordine basate soltanto sull'attrazione confermavano grosso modo solo metà del moto osservato dell'apogeo lunare, vale a dire 20° invece degli osservati 40° della precessione annuale. Sebbene questo risultato non fosse nuovo, giacché Newton l'aveva trovato senza equazioni differenziali nei suoi Principia, il calcolo dette animo ai critici di Newton.
Nell'aprile del 1748 Clairaut, che era membro della commissione, comunicò ad Euler che il tentativo di garantire le perturbazioni nell'orbita di Saturno causate da Giove solo con la legge di attrazione di Newton, gli avevano dato la vittoria del premio dell'Accademia di Parigi. Euler attribuiva i valori sbagliati ad osservazioni imprecise e soprattutto ad una piccola imprecisione nella legge dell'inverso del quadrato per le grandi distanze interplanetarie. Lieto che la memoria di Euler coincidesse con la sua, in novembre Clairaut raccomandò di correggere la legge dell'inverso dei quadrato di Newton, aggiungendo l'inverso della quarta potenza della distanza.
Ma dopo essersi reso conto che le approssimazioni del secondo ordine sono cruciali per determinare il moto dell'apogeo lunare, Clairaut scoprì che i suoi primi calcoli erano sbagliati e ritirò la propria affermazione che il moto della Luna è contrario all'attrazione newtoniana, annunciando questo nuovo risultato all'Accademia di Parigi nel 1749. Quando Euler lo seppe, rifece tutte le proprie derivazioni in luglio, senza trovare alcun errore. Era convinto che i propri calcoli fossero fuori di dubbio e quindi che Clairaut avesse torto.
Nel 1749, quando l'Accademia di San Pietroburgo gli chiese l'argomento della competizione da proporre per il 1751, Euler mandò un elenco di quattro, fra cui i membri scelsero il primo: se le differenze lunari sono in accordo con la teoria di Newton. Clairaut sottopose per la competizione l'articolo "Teoria della Luna dedotta dal solo principio dell'attrazione". Euler, che era il principale giudice lo lesse "con infinita soddisfazione" ed imparò il suo metodo. Riguardando le proprie ricerche sulla teoria lunare e sviluppando abbastanza le complicate approssimazioni del moto apsidale, scoprì l'origine del proprio errore. Egli lodò Clairaut, affermando che il suo lavoro era esemplare e che l'attrazione gravitazionale "è completamente sufficiente per spiegare il moto" dell'apogeo lunare. Questi studi lunari e l'articolo di Clairaut davano "nuovo lustro alla teoria [dell'attrazione gravitazionale] del grande Newton".[15] Ma Euler ospitava ancora l'idea, in parte dovuta ai suoi studi sul magnetismo, che fosse necessario un piccolo fattore correttivo, in questo caso trascurabile, alla legge dell'inverso del quadrato di Newton.
Anche se Euler non era molto popolare a corte, Federico II stimava la sua Matematica applicata ed i premi che vinceva all'estero. In una Storia del mio tempo, il re lo loda come "ornamento della corte". Alla fine della guerra di Successione austriaca nel 1748, Federico II assegna ad Euler altri progetti statali, di cui tre nel 1749. Era incaricato di trovare la maniera di livellare i 70 km del canale Finow, che congiungeva il fiume Oder con l'Havel. Quel canale rendeva Stettino un porto marittimo per la Prussia. Euler prese come assistente al progetto il proprio figlio quindicenne Johann Albrecht. Il suo rapporto si concentrò sulla regolazione della pressione nelle numerose chiuse. In settembre gli fu chiesto di aumentare la pressione idraulica nelle pompe e nei condotti delle fontane della residenza reale di Sans Souci a Postdam. Federico voleva che il getto d'acqua delle fontane ragiungesse l'altezza di cento piedi, in modo da essere confrontabile con i getti di Versailles. Euler trovò che forzando l'acqua a quei livelli, i tubi di legno, anche se rinforzati da fasciature metalliche, sarebbero esplosi, ma nel calcolo della pressione idraulica non tenne conto dell'attrito, con imbarazzanti risultati. In seguito, Federico dette la colpa del fallimento alla vanità della Matematica. Il 15 settembre, il re assegnò ad Euler un problema in ciò che oggi è Matematica ricreativa: progettare una lotteria per la Prussia. A seguito delle guerre recenti, il regno aveva bisogno di fondi per la pensione delle vedove.
Le entrate della lotteria sarebbero state d'aiuto. Euler lasciò da parte l'idraulica e, in due giorni, progettò la versione di una lotteria che offriva la possibilità di estrarre cinque numeri da un gruppo di novanta. Per questa lotteria egli calcolò il prezzo equo dei biglietti e l'aumento nei margini del profitto, anche se nel corso della propria carriera aveva prestato poca attenzione alla probabilità e in seguito scrisse solo otto articoli sull'argomento.
La lotta di Euler con i sostenitori di Wolff proseguì con l'affare Maupertuis-König, la principale disputa scientifica del secolo. La questione centrale riguardava la priorità del principio di minima azione, che ora viene detto di Euler-Maupertuis: apparteneva al grande Leibniz oppure a Maupertuis? Nel suo Saggio di cosmologia del 1750, Maupertuis riformulò la legge: "Tutte le volte che ha luogo un cambiamento in natura, la quantità di azione è sempre la minima". Egli la riteneva la legge finale della Meccanica, cercata da Descartes e Newton, e dichiarò che aveva applicazione universale ed era stata originata in tre suoi articoli delle Mémoires dell'Accademia di Parigi. Nell'articolo "Azione", nel primo volume dell'Encyclopédie nel 1751, d'Alembert sostenne la sua affermazione di universalità, ma in "De universali principio aequilibri et motu", apparso ancora nel 1751 nei Nova acta eruditorum di Lipsia, il matematico svizzero Johann Samuel König portò obiezioni al grado di applicazione del principio e quindi al risultato scientifico di Maupertuis, insieme alla sua integrità.
L'articolo di König sorprese Maupertuis che progettò una replica, insieme ad Euler ed al giovane svizzero Johann Bernard Merian, un instancabile alleato della Metafisica.
Euler, che di fatto era quello che meritava la priorità del principio, si dispose immediatamente alla difesa di Maupertuis. Maupertuis non aveva la capacità matematica per concepire le equazioni differenziali del principio e dunque Euler le fornì in una serie di articoli. I giornalisti della stampa tedesca e le facoltà universitarie in generale erano ostili a Maupertuis, soprattutto per la sua gestione autocratica dell'Accademia di Berlino.
Nel crescente dibattito, Euler fece ricorso all'autorità scientifica, mettendo in contrasto i risultati "dell'illustre presidente" con quelli "del professore", le cui conoscenze di Meccanica "erano degne soltanto di disprezzo"[16]. Egli liquidò i giornalisti alleati di König come "pubblici polemisti", privi della necessaria conoscenza per dare giudizi scientifici[17].
König basava la propria affermazione su una copia di una porzione di una lettere non pubblicata di Leibniz a Jacob Hermann a Basilea, dell'ottobre 1707, che definiva l'azione e sosteneva che le origini del principio di minima azione erano in Aristotele. Maupertuis gli chiese di mostrare la lettera originale e fece appello all'aiuto di Federico II, in quanto la disputa era un attacco all'accademia reale. Le ricerche si mostrarono infruttuose. Non fu trovata nessuna lettera. Al termine della ricerca, Maupertuis chiese una riunione straordinaria dell'Accademia, il 13 aprile 1752, ed invitò due curatori nobili a dirigerla. Intendeva restare assente. Per essere certo che i membri di lingua tedesca, non fluenti in francese, potessero capire, Euler lesse in latino la relazione su König [E186]. Fu pubblicata in francese: "Exposé concernent l'examen de la lettre de Leibniz" [E176]. Euler trovò insostenibile la posizione di König ed affermò che il frammento di lettera era "un falso, o per diffamare Maupertuis o per lodare in maniera esagerata il grande Leibniz, che non aveva bisogno di un simile aiuto"[18]. Soltanto la metà degli accademici partecipò alla riunione, ma quelli presenti sostennero all'unanimità il giudizio di Euler sulla lettera. La lettera in questione, ritrovata oltre un secolo più tardi, non presenta una versione completa del principio di minima azione.
In una serie di articoli, Euler e Merian difesero la decisione dell'Accademia, mentre numerosi giornalisti e facoltà universitarie tedesche ed olandesi vi si opposero. In due repliche, König respinse quella che definì la tirannia dell'Accademia e considerò il pubblico come "il suo giudice naturale".
Nel 1753, alla propria madre, che viveva in campagna, Euler comprò per 6.000 Reichsthaler una piacevole tenuta a Charlottenburg, una zona fuori Berlino, con residenze reale e nobiliari. Dopo la morte di suo fratello Heinrich nel 1750, l'aveva convinta a venire a vivere con lui. Quell'anno, Euler, Katherina e Albrecht raggiunsero a Francoforte il cugino olandese di Katherina, Johannes Michael von Loen, storico e teologo, per incontrare sua madre che era arrivata da Basilea. Come padre premuroso, Euler mandò i figli più giovani ed un tutore a vivere con la madre. Un decennio più tardi, gli accademici di Berlino introdussero la storia che, mentre lavorava, Euler aveva bambini piccoli che gli giocavano intorno. La sistemazione dei figli più piccoli, insieme al fatto che Albrecht non ricordi che, quando era giovane, il padre abbia mai fatto un lavoro domestico, elimina ogni dubbio.
Ma risulta che Euler avesse stretti contatti con i propri figli. Per rilassarsi, per esercizio e per pensare in solitudine, amava camminare spesso fino a Charlottenburg, che distava un miglio dalla sua casa di Berlino.
Dal maggio 1753 al luglio 1754 Euler operò come presidente dell'Accademia. Già in aprile Maupertuis aveva chiesto a Federico di poter "cedere gli aspetti amministrativi dell'Accademia al professor Euler, durante la mia assenza"[19] la cui integrità, intelligenza e zelo per l'istituzione giustificavano la designazione. Il re approvò la richiesta. Nel tentativo di ristabilirsi da una lunga malattia, Maupertuis stava sempre più a lungo lontano da Berlino, nella salubre "aria nativa" della Francia.
Dal 1754 l'influenza di Euler prese a estendersi oltre l'Accademia, alle università tedesche. Fiducioso nella capacità di Euler di riconoscere il talento scientifico, Federico lo incaricò di scegliere il successore di Wolff come professore e titolare della cattedra di Matematica all'Università di Halle. Sebbene Euler sapesse che Daniel Bernoulli avrebbe rinunciato, offrì il posto all'amico. In seguito nominò il matematico Johannes Andreas von Segner di Göttingen, un critico severo dei fondamenti matematici e scientifici della filosofia di Wolff.
In Astronomia, un settore importante della ricerca di Euler dal 1751 al 1756, una questione critica riguardava il fatto se il cambiamento secolare nel moto medio dei pianeti fosse ciclico o lineare. Per confermare che solo l'attrazione newtoniana spiega le operazioni meccaniche nel sistema solare, era essenziale risolvere il problema per i grandi pianeti Giove e Saturno. Nel 1752 Euler vinse ancora il premio dell'Accademia di Parigi per una memoria che usava un'algebra sbagliata per concludere erroneamente che Giove e Saturno stavano entrambi accelerando.
Nel 1755 apparvero in stampa le Institutiones calculi differentialis di Euler [E212]. Aveva completato questa seconda parte della sua trilogia sul Calculus nel 1748. Il Calcolo differenziale identifica i principi elementari e fu il primo testo ad organizzare sistematicamente il settore. Indica un vasto programma di ricerca per il calcolo differenziale e gli argomenti relativi. Allo scopo di valutare il suo impatto, occorre notare che, dopo sei anni, ben quattrocentosei delle cinquecento copie della prima edizione erano ancora invendute[20].
Un frequente argomento nella corrispondenza di Euler fino al 1756 fu l'elettricità. Egli cercava di conoscerne la causa fisica ed esaminava i rapporti sulle sue applicazioni mediche. Nel 1752 ottenne e studiò una copia di Experiments and Observations on Electricity, di Benjamin Franklin, in traduzione francese. Sicuramente aiutò il proprio figlio Johann Albrecht con l'articolo sull'elettricità che vinse il premio dell'Accademia di San Pietroburgo nel 1755.
La bravura di Euler nelle scienze matematiche era assistita da un forte interesse per la tecnologia scientifica, specialmente per la strumentazione ottica. Euler incoraggiò la costruzione di un telescopio di due piedi, con lenti progettate da lui stesso, allo scopo di riuscire a distinguere chiaramente i satelliti di Giove. Un risultato dei suoi studi sulle pompe ed il moto dei fluidi fu il suo sforzo di migliorare la teoria delle turbine, che presentò in dettaglio nella memoria "Teoria completa delle macchine che sono messe in moto dalla loro reazione con l'acqua" [E222], pubblicata nelle Mémoires dell'Accademia nel 1754. Un'altra difficile sfida per Euler fu lo sviluppo di un rifrattore acromatico per migliorare i telescopi.
Nell'agosto del 1755 Euler ricevette una lettera da un suo importante giovane collega, il diciannovenne Ludovico de la Grange Tournier, di Torino, più noto come Joseph-Louis Lagrange. La lettera era rivoluzionaria, con la sua proposta di un metodo per eliminare la noia delle considerazioni geometriche di Euler del Methodus inveniendi, riducendolo completamente a tecniche analitiche. La lettera aprì il periodo di quello che Euler rinominò calcolo delle variazioni. Lagrange perfezionò le proprie idee e le pubblicò nel volume per il 1760/61 della Miscellanea Taurinensia. Euler attese a pubblicare articoli su questo argomento, per dare il pieno merito della scoperta a Lagrange.
Dalla morte di Maupertuis, avvenuta nel 1759, Euler agì da presidente dell'Accademia di Berlino in stretto rapporto con Merian. Sperava di essere nominato presidente, ma i suoi rapporti con Federico si erano deteriorati. Sembra che il re non comprendesse che il lavoro matematico di Euler aveva un'importanza maggiore che gli scritti dei sapienti di Parigi. Aveva in mente un unico candidato, d'Alembert, che era un "philosophe, critico, editore scientifico della famosa Encyclopédie, uomo di nobili origini e francese"[21]. E queste due ultime cose erano senza dubbio di non piccola importanza per Federico. Alle scienze il monarca preferiva le facezie, il libero pensiero e la poesia - e questi non erano gli argomenti preferiti da Euler. In una lettera a d'Alembert relativa al pensiero dei matematici riguardo alla poesia, Federico scrive: "Un certo geometra, che ha perso un occhio facendo i calcoli, decise di comporre un minuetto con a per b. Se l'avesse suonato di fronte ad Apollo, la povera anima sarebbe stata scorticata viva, come Marsia"[22]. Forse a causa di un episodio autentico, il monarca scrisse con disapprovazione di "un certo figlio di Euclide" che a teatro fu distratto dai suoi calcoli anche nel corso delle scene più drammatiche.
Nel giugno del 1763, al proprio amico Gerhard Müller, segretario dell'Accademia di San Pietroburgo, Euler scrisse di d'Alembert, il quale aveva appena rinunciato a una posizione ben remunerata. Insieme ad altri sapienti francesi, aveva scelto di continuare con una piccola pensione a Parigi piuttosto che accettarne una maggiore a San Pietroburgo.
Riferendosi alla "insopportabile arroganza" di d'Alembert, Euler dichiara "di capire che non sia per niente adatto [alla presidenza]"[23]. Euler respinge come altezzosi gli sforzi di d'Alembert di contraddire la teoria idrodinamica di Bernoulli e definisce vergognose le sue dispute con Clairaut in Astronomia. Euler era preoccupato che d'Alembert raccomandasse come sostituto per la presidenza il cavalier Louis de Jaucourt, autore dell'articolo "Monarchia" nell'Encyclopédie, nel quale descriveva i limiti del potere reale. Questo avrebbe aperto la strada per l'ammissione all'Accademia di numerosi pensatori radicali francesi[24].
Più avanti, in giugno, d'Alembert, che si era già incontrato con Federico a Wesel nel 1755, ebbe un secondo incontro a Berlino. Per più di un decennio, facendogli doni monetari, il monarca lo aveva pregato di venire all'Accademia di Berlino. A corte c'erano difficoltà ad accogliere un così noto pensatore francese. Euler temeva il peggio, che d'Alembert o un altro francese fosse nominato presidente. Desideroso di porgergli rispetto, d'Alembert si incontrò con Euler e rimase colpito dalla sua enorme memoria, dalla sua conoscenza di un grande numero di formule computazionali dell'analisi e dalla chiarezza della sua logica. Non aveva intenzione di accettare la presidenza. Euler fu alquanto imbarazzato quando d'Alembert lo propose per essa, ottenendo un aumento di pensione. Con il suo salario, i premi in moneta e gli investimenti, Euler stava ora veramente bene. Rimase incantato dall'incontro con d'Alembert. In ottobre scrisse a Goldbach: "La nostra amicizia è perfetta, e non si possono ripetere abbastanza volte le belle cose che M. d'Alembert ha detto al re sul mio conto"[25]. Pur senza trasferirsi in permanenza a Berlino, attraverso la corrispondenza con Federico, d'Alembert divenne il "presidente segreto" dell'Accademia.
La crescente corrispondenza di Euler con Müller mostra che almeno fin dal 1761 egli considerava seriamente di tornare in Russia. La sua lettera del 17 maggio afferma che aveva venduto la sua proprietà di Charlottenburg per 8,500 Reichstahler, rendondosi libero di lasciare Berlino. Ma prima della fine della guerra non sarebbe stato in grado di accettare un'offerta da San Pietroburgo.
Dalla fine della guerra dei sette anni, avvenuta nel 1763, fino al 1766 Euler rimase a Berlino. Nel 1763 divenne il capo del potente Concistoro Franco Calvinista. Allo scopo di raccogliere fondi per l'economia prussiana, devastata dalla guerra dei sette anni, Euler raccomandò una nuova lotteria e si attivò come agente finanziario per aumentare la fabbrica di porcellane. In luglio, Caterina II ricevette dal consigliere dell'Accademia Grigoriz N. Teplov la proposta di tornare in Russia. Raccomandava che Euler diventasse segretario e direttore della classe Matematica dell'Accademia, con una pensione annua di 1,800 rubli, che Johann Albrecht fosse nominato professore ordinario con una pensione di 600 rubli, che la moglie di Euler ricevesse una pensione da vedova e che 500 rubli finanziassero il viaggio della famiglia a San Pietroburgo[26]. A quanto pare desiderando una pensione maggiore, Euler declinò l'offerta in luglio, ma continuò ad esprimere il proprio desiderio di un possibile ritorno. Ora voleva soltanto proseguire la propria ricerca. Nell'inverno del 1763/64 la posizione di Euler a Berlino era peggiorata. Riaffermando l'assolutismo in Prussia, Federico assunse la presidenza dell'Accademia. La scelta dei membri e la gestione delle finanze divennero questioni critiche. La posizione di Euler a Berlino era insostenibile. I suoi sforzi per l'autonomia della scienza in Prussia erano falliti. Nel dicembre del 1765 egli scrisse all'Alto Cancelliere della Russia, conte Michail Voroncov, descrivendo la propria situazione a Berlino e ponendo delle condizioni per il ritorno in Russia con la famiglia.
L'imperatrice Caterina II era un sovrano illuminato, che coltivava le arti, profondeva doni sull'Accademia delle scienze ed offriva protezione ai suoi membri. Per ottenere un immediato prestigio per la propria Accademia, voleva in particolare acquisire Euler. Ordinò all'ambasciatore a Berlino, principe Vladimir Dolgorukij, di negoziare con lui ed accettare la richiesta che gli avrebbe fatto. Euler pose condizioni finanziarie abbastanza dure per un uomo di scienza, chiedendo il doppio della precedente proposta di Caterina. Per uno studioso della levatura di Euler l'imperatrice pensò che fosse un affare. Dopo che Voroncov diede risposta positiva, nel gennaio del 1766, Dolgorukij la confermò. Ma Euler doveva prima ottenere il permesso di Federico. Le sue prime due richieste del febbraio 1766 furono accolte in silenzio, una nota strategia del sovrano. Con indipendenza e tenacia tutta svizzera Euler chiese altre due volte il permesso di partire. Dopo la terza lettera, Federico gli ordinò il 17 marzo di non insistere con le sue ripetute richieste.
Ma Euler non lo fece. Anzi, la sua lettera del 30 aprile chiese che a lui ed ai suoi figli Johann Albrecht e Karl fosse permesso di tornare in Russia. Senza neppure una parola di ringraziamento, in maggio Federico scrisse solo due righe: "Vi permetto di rinunciare e tornare in Russia"[27]. Probabilmente il re non voleva contrastare senza motivo "la cara sorella" Caterina II.
Di grande rilievo nell'attività scientifica che aveva occupato Euler durante i suoi anni a Berlino dopo il 1760 è la raccolta di 234 lettere, in seguito intitolata Lettere a un Principessa tedesca [E343, E344, E417] spedite dal 1760 al 1762. All'inizio della corrispondenza, la principessa Charlotte, figlia del futuro margravio Friedrich Heinrich von Brandenburg-Schwedt, aveva quindici anni. Le lettere, scritte in francese, si rivolgono alla filosofia naturale, vale a dire alle scienze, oltre che alla filosofia ed alla religione. Hanno una suddivisione naturale in tre parti: 1-79, su argomenti di Musica, aria, Ottica, gravità, Cosmologia, le maree e la Teoria della materia, in particolare la proprietà di incompenetrabilità e le monadi; 80-133, comprendenti libertà, spirito, Cristianesimo, linguaggio, sillogismi, diavolo, felicità, certezza delle verità scientifiche, morali e storiche, fondamenti di conoscenza, divisibilità e monadi; 134-234, che coprono elettricità, magnetismo, lenti, telescopio, microscopio e distanze stellari.
Le Lettere costituiscono un'alta divulgazione che presenta la visione sintetica di Euler sulle scienze, congiunta alla sua originale comprensione profonda. Egli esamina in grande dettaglio le maggiori filosofie naturali, di Cartesio, di Newton, di Leibniz e di Wolff, in maniera migliore di qualunque altra esposizione popolare. Euler difende fortemente la propria concezione religiosa nei confronti dei liberi pensatori e degli enciclopedisti francesi[28].
Le Lettere a un Principessa tedesca non furono stampate fino al 1768 e 1772 a San Pietroburgo, probabilmente perché Federico era in situazione critica con il margravio.
Scritte in maniera avvincente e con grande chiarezza, il lavoro ebbe uno straordinario successo. Prima del 1800 fu tradotto dall'originale francese in altre otto lingue: russo, tedesco, olandese, svedese, italiano, inglese, spagnolo e danese. Prima del 1840 arrivò alla quarantesima edizione.
Nel 1765, Euler pubblicò Theoria motus corporum solidorum [E289]. Questo lavoro fondamentale, collegato alla sua Mechanica in relazione alla Meccanica del punto materiale, viene spesso detto la sua seconda meccanica. È la parte finale del suo programma su un argomento che lo impegnò circa trent'anni per essere completato. Aveva in precedenza dato le equazioni differenziali per il moto dei corpi fluidi, elastici e flessibili. La Theoria motus corporum solidorum presenta chiaramente ed in dettaglio la sua revisione analitica dell'intera teoria dei corpi rigidi.

Durante il regno di Caterina II La Grande: la seconda volta a S. Pietroburgo

La famiglia Euler arrivò a San Pietroburgo il 28 luglio 1766. Egli aveva cinquantanove anni. Una appariscente Caterina II lo ricevette in vesti regali, andando oltre i termini del contratto. Gli mandò 10,800 rubli per comprare una grande casa a due piani, completa di mobilio, sulle rive della Grande Neva, vicino all'Accademia, apposta per lui e la sua famiglia. Nel 1765 la Russia aveva subito una grossa perdita nelle scienze con la morte di Michail Lomonosov. Euler ed Albrecht cominciarono con successo l'opera di riabilitazione dell'Accademia. Caterina, che aveva già consentito ad assumere altri otto accademici, promise ad Euler di riorganizzare l'istituzione in modo da darle maggiore autonomia di ricerca scientifica, oltre a ridurre le lotte interne. Come membro più anziano e più insigne, egli doveva presiedere tutte le riunioni ed era responsabile della selezione dei nuovi membri.
Nel maggio del 1771, a San Pietroburgo scoppiò un grande incendio che distrusse 550 case, compresa quella di Euler. Nella confusione generale, l'indifeso e quasi cieco Euler, con la sola biancheria da notte, avrebbe potuto morire se il suo tuttofare Peter Grimm non fosse corso nella casa a salvarlo. La biblioteca ed il mobilio erano distrutti, ma il conte Vladimir Orlov salvò i manoscritti. Caterina rimborsò Euler con 6,000 rubli per comprare una nuova casa - cosa che fu fatta rapidamente. Nel settembre del 1771 subì un'operazione ad un occhio, per via di una cataratta che lo rendeva quasi cieco. Johann Albrecht e nove medici gli si raccolsero intorno per osservare la breve operazione. Il recupero della vista dall'occhio sinistro portò un momento di sollievo, ma in ottobre una complicazione, forse un'infezione, lo lasciò praticamente cieco ed a volte dolorante. Euler descrisse la perdita della vista come "una distrazione in meno". Poteva ancora fare a mente difficili calcoli, ad esempio sommare serie infinite fino a cinquanta termini. L'Accademia si riuniva tre volte alla settimana. Egli fu assente dal settembre 1771 al maggio del 1772, quando riprese a partecipare.
Nel 1773 Euler chiese a Daniel Bernoulli di raccomandargli un assistente di Basilea.
Era fiero di non aver mai perso il proprio accento svizzero ed amava usare il dialetto di Basilea. In luglio, Bernoulli mandò Nicholas Fuss a vivere con lui ed a fungere da segretario personale. Fuss sarà la persona più vicina ad Euler nel decennio finale della sua vita e nel 1784 sposerà la sua nipote Albertina[29], la seconda figlia di Albrecht.
Nel novembre del 1773, all'età di sessantasei anni, morì la moglie di Euler, Katharina.
La perdita complicò enormemente la vita domestica, perché Katharina dirigeva tutto ed egli non faceva niente. Euler era determinato a rimanere indipendente e non a far conto sui figli, nonostante a quel tempo le abitudini di una persona anziana fossero quelle di risiedere con i figli e rimanere sotto la loro cura. Sapendo che i suoi figli si sarebbero opposti, nel Natale del 1775 Euler affrontò l'argomento di un secondo matrimonio. Conscio che la società di San Pietroburgo non avrebbe capito la sua scelta, lo bloccarono. Adesso Euler soffriva di un'altra febbre alta, e rimase sotto la cura del figlio Karl per due settimane. Nel luglio del 1776 Euler annunciò semplicemente, senza consultarsi con alcuno, il proprio imminente matrimonio con la sorellastra di Katharina, Salome Abigail, di cinquantatre anni. A San Pietroburgo la famiglia Euler seguiva la chiesa riformata, essenzialmente calvinista, che probabilmente aveva sede vicino all'Accademia ed alla sua casa[30]. Il pastore celebrò le nozze a casa di Euler.
Nell'estate del 1778, Johann III Bernoulli fece visita a Euler. Nel proprio diario, Bernoulli annota che la salute generale di Euler restava buona, ma la sua vista era tanto cattiva che non riusciva a riconoscere i volti. Ancora tuttavia era in grado di scrivere chiaramente a grossi caratteri sulla lavagna, meglio di molte persone con la vista buona.
Durante il suo secondo periodo a San Pietroburgo, un ancora energico Euler divenne sempre più prolifico negli articoli. Dopo il 1765 completò più del cinquanta per cento di tutte le sue memorie. Neppure la quasi cecità lo rallentò. Al proprio servizio aveva genio, intuizione della materia e fenomenali memoria ed abilità nei calcoli mentali, insieme ad un piccolo gruppo di ricercatori formato dai suoi figli Albrecht e Christoph, oltre ad Anders Johann Lexell, Wokfgang Ludwig Krafft, Semjon Kirillovic Kotel'nikov e Rumovskij. Si aggiunsero poi Michail Evseevic Golovin e soprattutto Fuss, che nel 1774 Euler raccomandò perché venisse accolto all'Accademia. Il padre di Krafft, Georg, aveva collaborato con Euler durante il suo primo periodo a San Pietroburgo, e Golovin era un parente di Lomonosov.
Euler fissava l'argomento e il problema iniziale di ciascuno dei suoi articoli teorici, per lo più in modo succinto. Il gruppo di ricerca lavorava alla sua residenza, attorno ad una grande tavola con una lavagna nel mezzo. Anche se Euler era in grado di scrivere su di essa a grandi caratteri, a quanto sembra la usavano soprattutto i suoi assistenti. Quand'era solo, il quasi cieco Euler camminava intorno ad essa per esercizio. Durante le sedute di lavoro, i partecipanti facevano i conti ed Euler li rivedeva per eliminare gli errori. In seguito tutti gli articoli sulla tavola venivano messi in una grande cartella. Soprattutto Fuss e Golovin prendevano nota di ciò che Euler dettava. Fuss fece anche i calcoli in più di 160 articoli di Euler pubblicati dopo il 1766, e Golovin in più di 70. Inoltre, alcuni articoli hanno la grafia dei suoi figli. Trecento articoli del secondo periodo di San Pietroburgo sono apparsi dopo la sua morte.
Fino al 1773 Euler scrisse libri, sebbene la sua corrispondenza calasse precipitosamente. Aveva completato a Berlino tre dei quattro libri che cominciarono ad essere pubblicati nel 1768. Il primo volume delle Institutiones calculi integralis, stampato nel 1768 [E342], ed il secondo nel 1769 [E366] comprendono complessivamente l'ultima parte della sua grande trilogia sul Calculus. Contengono centinaia delle sue scoperte sulle equazioni differenziali ordinarie e parziali. Il volume tre [E385] sul calcolo delle variazioni, che segue i metodi analitici di Lagrange, fu pubblicato nel 1770. Lexell lo aiutò a pubblicare la Diottrica [E367, E386, E404], in tre volumi, dal 1769 al 1771. L'influente Introduzione completa all'algebra [E387, E388] apparve in russo nel 1768 e 1769 ed in tedesco l'anno successivo.
Avrà anche edizioni in inglese, olandese, italiano e francese. Dal 1770 Euler preparò le 775 pagine della Theoria motuum lunae. L'ultimo libro di Euler, Trattato sulla costruzione e manovra dei vascelli, fu pubblicato in Francia l'anno successivo. A questo punto la sua corrispondenza era calata a non più di venti lettere l'anno. La sua corrispondenza con Lagrange, importante sorgente di ricerca in teoria dei numeri, analisi e meccanica, ebbe termine nel marzo del 1775, su argomenti di integrali ellittici, paradossi dell'integrazione e dimostrazioni dimenticate di Fermat. Dopo il 1777 egli spedì meno di cinque lettere l'anno. Dal 1775 al 1782, al conte Vladimir Orlov, direttore dell'Accademia dal 1766, succedette un suo sostenitore, il poeta minore Sergej Domasnev. I fratelli Orlov avevano partecipato al colpo di Caterina contro il marito nel 1762, ed ella li aveva ricompensati con la posizione. Nessuno dei due tollerava le istituzioni. Orlov credeva che l'Accademia fosse inutile e che le scienze rendessero il mondo peggiore. Domasnev era simile a Schumacher: arrogante, scurrile e dissipatore di fondi. Disgustato, Euler cominciò a ritirarsi dagli affari dell'Accademia sotto Orlov, lasciando il posto di capo della commissione accademica nel 1774. Come mostrano i Protocolli, sotto Domasnev, nel gennaio del 1777, cessò del tutto di frequentare le riunioni. Tuttavia continuò a sottoporre un flusso di articoli letti da Krafft, Fuss e Golovin, su argomenti quali l'orbita lunare, l'integrazione delle formule irrazionali, le frazioni continue ed i paradossi del calcolo delle variazioni. Dopo che Domasnev non aveva risposto ad una lettera degli accademici che protestavano per la rottura delle regole protocollari, nel dicembre del 1782 mandarono alla commissione accademica una lettera che lamentava le sue azioni ed Euler aggiunse il proprio nome a quelli dei firmatari. Dopo due mesi di inchiesta, Domasnev fu rimosso. Gli accademici non potevano più essere trascurati politicamente.

Nel gennaio del 1783, la principessa Caterina Romanova Daskova, una favorita di Caterina II, fu nominata direttore dell'Accademia e chiese che, insieme ad Albrecht ed a Fuss, la persona che chiamava "il grande Euler" la accompagnasse sulla sua carrozza alla prima seduta. Pregò Euler, che si sentì onorato, di riuscire ad entrare nell'Accademia al suo braccio e presentarla.

Fuss guidava i passi di Euler. La sua presenza mosse gli accademici alle lacrime. Quando un altro professore, Jakob Sthälin, occupò il posto d'onore accanto al direttore, la principessa Daskova si girò verso Euler e, per la delizia di suo figlio e di Fuss, disse: "Sedetevi dove volete ed il posto che scegliete sarà naturalmente il primo di tutti" [31]. Questa fu la sua ultima seduta. Con il sostegno di Caterina la Grande, l'Accademia di San Pietroburgo aveva cominciato a rendere omaggio ad Euler durante la sua vita, commissionando per l'aula dell'assemblea un murale allegorico sulla saggezza della Geometria, che includeva un pannello ornato di formule e calcoli presi dalla seconda teoria lunare di Euler - a quel tempo una straordinaria onorificenza per un uomo di scienza. Fino alla sua morte, il 18 settembre 1783, Euler rimase entusiasta e perspicace sia nella ricerca che nell'insegnamento. Spiegava Matematica elementare a quattro suoi nipoti e l'ultima mattina stava istruendo un nipote dotato nelle scienze e faceva calcoli a mente che poi scriveva alla lavagna del suo studio su quanta aria calda occorresse ad un pallone per alzarsi. Erano appena arrivate a San Pietroburgo, ed erano diventate l'argomento del giorno all'interno della repubblica delle lettere, le notizie del successo dei fratelli Montgolfier sull'ascesa del pallone sopra Parigi. Euler fece colazione col proprio assistente Fuss, con Lexell e la sua famiglia. Lexell doveva diventare il suo successore. Discussero dell'orbita del pianeta Urano, che William Herschel aveva appena scoperto nel marzo del 1781, un altro argomento che assorbiva il pubblico europeo colto. Euler si divertiva a dettare calcoli di aerodinamica e relativi all'orbita del pianeta di Herschel che i suoi assistenti avrebbero messo sulla lavagna. Intorno alle cinque, all'ora del tè, aveva giocato un po' col proprio nipote. Beveva tè e fumava la pipa. Improvvisamente la pipa gli cadde dalle mani. "La mia pipa", disse e si piegò per raccoglierla. Non riuscì e si alzò in piedi. Per un anno Euler aveva sofferto di vertigini e di cattiva salute. Ora ebbe un colpo. Raccogliendo le mani sulla pancia, disse "Sto morendo" e perse definitivamente conoscenza. Morì verso le undici di quella sera. Aveva sessantasei anni. Vent'anni prima, riflettendo sullo stato della coscienza dopo la morte, Euler aveva supposto che avvenisse una sospensione dell'unione fra corpo ed anima, nella quale i sensi influenzano anche i nostri sogni. Nella morte, egli credeva, "ci troveremo in un più perfetto stato onirico"[32].
Euler fu cremato sull'isola Vasilevskij, nella sezione luterana del cimitero Smolensk, che era riservato soprattutto ai membri della chiesa ortodossa russa. Le quattro maggiori accademie reali delle scienze, Berlino, Londra, Parigi e San Pietroburgo, ed anche le società di Lisbona e di Torino alle quali apparteneva, annunciarono la grande perdita.
Antoine-Nicolas de Condorcet, segretario dell'Accademia delle Scienze di Parigi, Fuss a San Pietroburgo e Formey a Berlino tennero i principali necrologi. Il 23 ottobre 1783, l'Accademia Imperiale delle Scienze di San Pietroburgo si riunì in memoria di Euler. Presiedette la principessa Daskova e partecipò un arcivescovo, insieme a numerosi nobili dignitari. Nel corso del necrologio, Fuss descrisse la vita di Euler come un trionfo dello spirito umano e l'uomo come esemplare nello sforzo del suo secolo di "illuminare il mondo"[33]. Su richiesta della principessa, gli ufficiali dell'Accademia Imperiale onorarono materialmente la memoria di Euler installando nel 1785 un busto di marmo a mezza altezza, fatto da Jean-Dominique Rachette, nella sale della biblioteca della "Kunstkammer". Euler aveva promesso al conte Orlov di preparare abbastanza articoli per i prossimi venti anni negli Acta e nei Nova Acta dell'Accademia, ma ne lasciò abbastanza per oltre quaranta, trascritti dai suoi assistenti. Fino al primo decennio del diciannovesimo secolo la modesta pietra tombale di Euler non poteva essere riconosciuta nel cimitero Smolensk, nemmeno da Fuss, che aveva partecipato al funerale. La tomba di Euler non fu riscoperta fino al 1830, alla sepoltura di una sua nuora. Nel 1837 l'Accademia la sostituì con un monumento di marmo finlandese rosa, con la semplice dicitura Leonhardo Eulero, Academia Petropolitanae, per uno studioso che, secondo Turgot, aveva "onorato l'umanità con il suo genio e la scienza con il suo stile"[34].

Note

1. Nicholas Fuss, "Lobrede auf Herrn Leonhard Euler", in OO I.1, pp. XLIII-XCV.
    
2. Karin Reich, "Gauss' geistige Väter: nicht nur `summus Newton' sondern auch `summus Euler'," in Wie der Blitz einschlägt, hat sich das Rél gelöst, Göttingen: Niedersächsische Staats- und Universitätsbibliothek, 2005, pp. 105-115.
    
3. Tutti, tranne venti degli 868 articoli e libri di Euler, sono elencati nell'indice Eneström. Di questi, 819 riempiono 74 volumi dal 300 alle 600 pagine ciascuno, nella prima serie della sua Opera Omnia (abbreviata OO). Nel materiale non ci sono essenzialmente ripetizioni. La Serie Uno, sulla matematica pura, è di 29 volumi in 30 parti; la Serie Due, sulla meccanica e l'astronomia, 31 volumi in 32 parti. La Serie Tre, fisica e miscellanea, è composta da 12 volumi. La Società Scientifica svizzera ha cominciato l'Opera Omnia nel 1907. Euler ebbe una disavventura: sei scatole piene di suoi lavori andarono perse nel 1766, durante una spedizione attraverso il mar Baltico, verso San Pietroburgo. Nel 1802, erano pubblicati 707 lavori di Euler. Nel 1975 è cominciata una quarta serie dell'Opera in due parti, il cui progetto consiste di almeno 10 volumi. La Sezione A ha cominciato a rendere accessibili le oltre 2.840 lettere rimaste, da e verso di lui, in francese, latino, tedesco, russo ed inglese. La Sezione B esaminerà i suoi 12 quaderni di note ancora esistenti. Tenendo conto di frammenti scoperti nei quattro decenni passati, si arriva a 886 lavori.
   Si veda anche Rüdiger Thiele, "The Mathematics and Science of Leonhard Euler (1707-1783)" in Glen van Brummelen e Nichael Kinyon eds, Mathematics and the Historian Craft, Berlin: Springer, 2005, pp. 81-140, che include una vasta bibliografia, e Clifford Truesdell, "Leonhard Euler, Supreme Geometer (1707-1783)", in Harold E. Pagliaro ed, Irrationalism in the Eighteen Century, Cleveland: Case Western Reserve U. Press, 1972, pp. 53-54.
    
4. Leonhard Euler, "Autobiography", in Emil Fellmann, Leonhard Euler, Reinbeck bei Hamburg: Rowoht Taschenbuch Verlag, 1995, pp. 11-13.
    
5. Citato da Emil Fellman, Leonhard Euler, pp. 11-13.
    
6. Eli Maor, e, Story of a Number, Princeton U. Press, 1994, p. 151.
    
7. Si veda anche Clifford Truesdell, "The Rational Mechanics of Flexible or Elastic Bodies, 1638-1738", in OO II.11, parte 2, particolarmente pag. 15-141.
    
8. Paul Heinrich Fuss, ed., Correspondance mathématique et physique de quelques célèbres du XVIIIéme siècle, New York: Johnson Reprint Corporation, 1968, 1st ed. 1843, vol. II, p. 85.
    
9. Mario Biagioli, Galileo Courtier: the Practice of Science in the Culture of Absolutism, Chicago: U. Chicago Press 1993, cap. 1.
    
10. Constantin Carathéodory, prefazione a OO, I.24, p. XI.
11. Anche se evidentemente egli non l'ha mai scritta in forma moderna, questa relazione è ormai detta identità di Euler. Oggi è solitamente scritta come eiπ+1=0 e Richard Feynman l'ha chiamata "la più notevole formula della matematica" perché collega cinque importanti costanti matematiche ed ha significative applicazioni, ad esempio per fornire ulteriori dimostrazioni rigorose sull'infinità dei numeri primi. (Paul J. Nahin, An Imaginary Tale: The Story of p¡1, Princeton U. Press 1998, p. 67).
     
12. Più di un secolo dopo l'identità di Euler sarà essenziale per riconoscere in maniera rigorosa che non ogni numero reale è radice di un'equazione algebrica: che esistono numeri trascendenti. Nel 1873 Charles Hermite dimostrerà che e è trascendente ed in seguito l'attenzione si sposterà su π, che da tempo destava il sospetto di essere dello stesso tipo. Basandosi sulla formula di Euler, Ferdinand Lindemann fu il primo a dimostrare la trascendenza di π. David Hilbert migliorò in seguito la dimostrazione.
     
13. Nel capitolo 21 di [E102] ad esempio, Euler cita i paradossi che rendono difficile l'estensione del dominio della funzione logaritmica all'insieme dei numeri complessi.
     
14. Si veda Robert E. Bradley, "Euler, d'Alembert and the Logarithm Function", in "Leonhard Euler: Life, Work and Legacy" (R.E. Bradley e C.E. Sandifer eds), Elsevier 2007.
     
15. OO, II.24, p. 1.
     
16. Mary Terrall, The Man Who Flattened the Earth: Maupertuis, vol. 1, p. 497.
     
17. Ibid., pp. 300-301.
     
18. Louis Gustave du Pasquier, Leonhard Euler et ses amis, Paris: J. Hermann, 1927, p. 105.
     
19. Lettera del 24 aprile 1753 a David Köhler, citata da Du Pasquier, Leonhard Euler et ses amis, p.110.
     
20. Clifford Truesdell, An Idiot's Fugitive Essay on Science, Berlin: Springer Verlag 1984, p. 296.
     
21. Adolf Harnack, Geschichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin, vol.1.1, p. 355.
     
22. Citato in Du Pasquier, Leonhard Euler et ses amis, p. 116.
     
23. 23 OO, IVA.1, R1885, p. 314.
     
24. OO, IVA.1, p. 313.
     
25. Paul Heinrich Fuss, ed., Correspondance mathématique et physique, du quelques célèbres géomètres du XVIIIéme Siècle, p. 668.
     
26. OO, IVA.1, p.438
     
27. OO IVA.6, p.393
     
28. Si veda Ronald Calinger, "Euler's Letters to a Princess of Germany As an Expression of his Mature Scientific Outlook", Archive Hist. Exact. Sci., 15, 1976, pp. 211-233, e Andreas Speiser, Leonhard Euler und die deutsche Philosophie, Zurich: Orell Füssli, 1939.
     
29. (1766-1829). Il loro figlio maggiore, Paul Fuss (1798-1855) fu il segretario permanente dell'Accademia.
     
30. Euler Johann Albrecht e Fuss tentarono invano di por fine a una divergenza fra i membri francesi, svizzeri e tedeschi della chiesa.
     
31. Principessa Ekaterina Daskova, The Memoirs of Princess Dashkova, tradotto ed a cura di Kyril
    Fitzlyon, Durham: Duke U. Press, 1995, p. 334.
32. Leonhard Euler, Letters... Addressed to a German Princess, New York: Harper, 1840, vol. I, p. 310.
33. Nicholas Fuss, "Lobrede auf Herrn Leonhard Euler", tradotto da John S.D. Glaus, pp. 1-2.
     
34. Lettera del 23 agosto 1774 di Turgot a Luigi XVI, citato in Nicholas Fuss, "Lobrede auf Herrn Leonhard Euler", p. 22.