L'espressione dell'arte nella Matematica: la catenaria
Pubblichiamo la "tesina" dell'Esame di Stato di Roberto Sala, che ha maturato l'idea di questo elaborato durante il Corso di Orientamatica 2016/2017. Nel contributo si analizza la scoperta, dal punto di vista matematico, della funzione catenaria e la sua successiva applicazione in architettura. Inoltre è presentata un'animazione con Geogebra della defizione di catenaria.
Il tema affrontato nella presente trattazione riguarda la scoperta, dal punto di vista matematico, della funzione catenaria e la sua successiva applicazione in architettura. Pur essendo un argomento poco conosciuto, è sorprendente come il tutto parta da un oggetto di uso comune e dalla curiosità di uno scienziato del XVII secolo, che per primo cercò di definirne una funzione matematica che ne descrivesse l'andamento: la traiettoria descritta da un filo appeso alle sue estremità, ipoteticamente inestensibile e flessibile, sottoposto soltanto al proprio peso. Questo scienziato fu Galileo Galilei che, non potendone dimostrare l'effettivo andamento, argomentò qualitativamente della curva descritta a partire dalla "catenella" (questo fu lo strumento utilizzato dal fisico pisano) approssimandola ad una funzione a lui ben nota, la parabola.
Successivamente, alcuni dei matematici più importanti di fine '600 riuscirono, effettivamente, a descriverne il reale andamento nel piano, definendone da canonica funzione
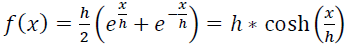
soprattutto grazie alle recenti scoperte in materia di calcolo infinitesimale, successive alla morte di Galileo.
Più di due secoli dopo, un architetto trentunenne fu in grado di sfruttare appieno la caratteristica peculiare di questa curva: la catenaria distribuisce, lungo tutto il suo arco, il proprio peso in modo omogeneo, proprietà dovuta al fatto che la tensione in ogni punto è sempre tangente alla traiettoria della curva. Questo architetto fu Antoni Gaudí che, ancora giovane, realizzò il progetto di quella che sarebbe diventata un'impressionante chiesa, simbolo della città di Barcellona: la Sagrada Familia.
Ricordando che la catenaria può essere definita come il "luogo dei punti descritti dal fuoco di una parabola che ruora e trasla lungo una retta", ecco un'animazione con Geogebra che applica la suddetta definizione:
