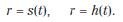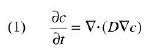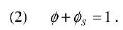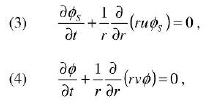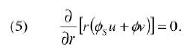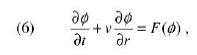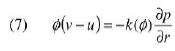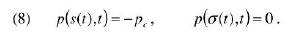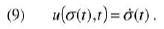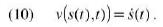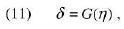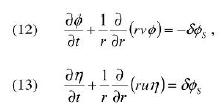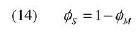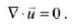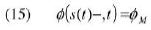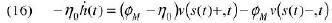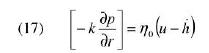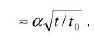Mentre cuociono gli spaghetti...
Molti conosceranno il libro La Matematica in Cucina di Enrico Giusti [1], nel quale l’autore ci invita a guardarci intorno per scoprire quanta Matematica suggeriscano gli oggetti che normalmente si trovano in cucina. Se proviamo a fare un passo oltre e accendiamo i fornelli per guardare con occhio matematico i processi di cottura, allora andiamo incontro a sfide tanto ardue quanto affascinanti.
Scopriamo così che il forno (qualunque tipo di forno) è un autentico laboratorio matematico. Pensate per esempio alla cottura del pane. La pasta lievitata è un mezzo poroso deformabile ricco del biossido di carbonio (CO2) sviluppato dai batteri del lievito (altro interessante problema matematico) e che contiene ovviamente un considerevole quantitativo di acqua. Portata alla temperatura di ebollizione, questa libera vapore. Il vapore e la CO2 aumentano la propria pressione al crescere della temperatura, causando la formazione delle bolle visibili nella mollica e la conseguente crescita di volume. Al tempo stesso la superficie esterna, maggiormente esposta al calore, subisce dei cambiamenti di struttura, dando origine alla crosta. Tutti questi fenomeni avvengono simultaneamente alla trasmissione del calore verso l’interno del pane, allo spostamento delle componenti gassose attraverso i pori e all’espansione della pasta e sono tra loro intimamente collegati. E non abbiamo ancora accennato alla conversione dell’amido ad una forma commestibile (ci ritorneremo sopra proprio per i nostri spaghetti). Troppo complicato? Risposta affermativa, tanto che i non molti lavori che si trovano in letteratura non credo abbiano dato risposte definitive [2].
L’istinto del fornaio resta per ora insostituibile. È chiaro che il pane è solo un esempio. Potete aggiungerci biscotti, torte, ma non solo: la Matematica dell’arrosto non è molto più semplice. La differenza principale è l’assenza di CO2 ma il sangue che impregna la carne ha un elevato contenuto di acqua e quindi siamo ancora alle prese con la formazione e la migrazione del vapore. Anche qui esisterà un “fronte di cottura” (abbastanza ben visibile al confine tra la zone rossa e quella più scura). Un’altra differenza riguarda la “crosta”: quella del pane è friabile e praticamente trasparente al vapore mentre tutti sanno che, per avere un arrosto “succulento”, è bene dare una bella “scaldata” all’inizio con lo scopo di rendere meno permeabile la superficie e limitare la perdita di liquidi.
Mentre si scalda l’acqua per i nostri spaghetti, accendiamo il gas sotto una padella con l’olio e al momento buono buttiamoci delle patate a fette. Dopo brevissimo tempo le patate cominciano a “friggere”, ossia ad emettere un intenso flusso di vapore che produce le caratteristiche scoppiettanti bolle (e i conseguenti schizzi). Poi si forma la croccante crosta esterna. Ma quali fenomeni stanno avvenendo nelle nostre patate? Per capirlo dobbiamo pensare che la patata non è altro che un mezzo poroso saturo (la parte solida è sostanzialmente amido ed è imbevuta d’acqua). Il trasporto di calore dall’olio verso l’interno produce due zone: una esterna in cui la temperatura è superiore a quella di ebollizione dell’acqua e una interna a una temperatura inferiore. Sul fronte di separazione avviene la transizione di fase liquido-vapore. Ma qual è la temperatura di ebollizione dell’acqua?
Se ponessimo la domanda a una scolaresca di bambini, vedremmo subito tante manine alzate: “Lo so, lo so: 100°C” (alla pressione atmosferica standard, aggiungeremmo noi). Invece è proprio qui che cominciano le difficoltà. Infatti il vapore viene espulso con una certa vivacità, segno che è presente un considerevole gradiente di pressione che ne guida il moto verso l’esterno. Questo si realizza grazie al fatto che la temperatura e la pressione sul fronte di ebollizione non sono costanti ma crescono entrambe,man mano che il fronte avanza all’interno. Sono tra loro legate da una legge di tipo esponenziale (legge di Clapeyron) che ci mostra che un piccolo aumento di temperatura può provocare un grande aumento di pressione del vapore. Ora vediamo bene che non soltanto dobbiamo descrivere la propagazione del calore nella patata, lo spostamento del fronte di ebollizione verso l’interno e il moto del vapore verso l’esterno ma dovremo pure determinare questa ulteriore incognita: la temperatura sul fronte di ebollizione. Difficile, sì, ma questa volta fattibile. Se vi siete incuriositi, leggete il lavoro [3], dove si formula il modello matematico e (con un certo orgoglio) si “fittano” i dati sperimentali degli ingegneri, meglio di quanto i medesimi fossero riusciti a fare prima. Oppure, se volete fare prima e soffrire meno, leggetevi l’articolo divulgativo su SIAM News [4].
Finora le cose sono andate benino proprio perché la nostra fetta di patata era abbastanza spessa (non una “patatina”) da non subire deformazioni. Se invece avessimo voluto friggere della “pastella”, ci saremmo trovati in notevoli difficoltà: “coccoli” e “panzerotti” sono ancora lì che aspettano il loro modello matematico perché per loro (come per il pane) la frittura si accompagna a grandi deformazioni. A proposito della frittura, prima di lasciarla vale la pena osservare che la particolare natura della legge di scambio di calore olio-patata sulla superficie esterna, sulla quale non ci possiamo intrattenere, suggerisce che quando un corpo scambia calore con l’esterno in un modo che dipende dalle proprietà fisiche della sua superficie (a loro volta influenzate dalla temperatura) si possono verificare curiosi fenomeni di tempi d’attesa. Mi spiego meglio: supponete che un corpo abbia una superficie “bianca” (che assorbe poco calore) sopra una certa temperatura T* e “nera” (che scambia molto calore) al di sotto di essa. Supponiamo che la sua temperatura iniziale sia inferiore a T* ed esponiamolo a una temperatura esterna superiore a T*. Nel momento in cui la superficie raggiunge la temperatura critica il profilo interno di temperatura mostra un gradiente elevato, compatibilmente con il fatto che la superficie è “nera”. Se la superficie diventasse immediatamente bianca, la quantità di calore condotta dall’esterno verso l’interno diventerebbe incompatibile con il flusso di calore stabilitosi internamente. Perciò è necessario che l’evoluzione della temperatura superficiale si arresti per dare modo alla superficie di evolvere attraverso una gamma di “grigi”. Durante questo tempo, il gradiente termico interno si attenua fino a diventare compatibile con lo stato di superficie “bianca”: solo allora riprenderà l’evoluzione termica normale. Ecco che il problema della patata fritta finisce per aprire la strada a considerazioni molto più generali e certo non banali sulla classica teoria degli scambi termici. Questo concetto è stato illustrato in [5], [6]. Lo cito perché è un bell’esempio di come, nel bel mezzo della costruzione di un modello, la Matematica ad un certo punto prenda le redini e sia lei a portarti a spasso nella direzione che più le piace. Nel caso della patata, il “cambio di colore” (da nero a bianco) è dovuto all’azione di schermo termico esercitata dal vapore in uscita.
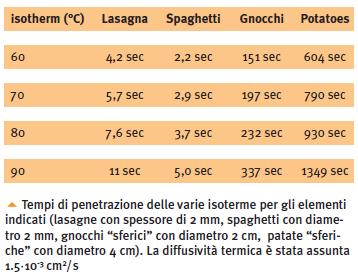
Dopo tutte queste digressioni l’acqua ha certamente cominciato a bollire (il che ci garantisce una temperatura di 100°C, con le solite precisazioni). Adesso vi invito a fare un esperimento che io stesso ho fatto in cucina prima di cominciare a lavorare sugli spaghetti: “buttate” la pasta (chissà perché si dice così) e abbiate cura di scegliere spaghetti abbastanza spessi (diciamo 2mm di diametro). La prima cosa che notate è che fate una certa fatica ad affogare gli spaghetti, a causa della loro rigidità. Questa però si attenua dopo pochi secondi, consentendovi di immergere gli spaghetti totalmente nell’acqua bollente. Si tratta dell’effetto della temperatura sulle caratteristiche meccaniche della pasta secca. Infatti si può calcolare che lo spaghetto assume praticamente la temperatura dell’acqua in pochi secondi. A questo proposito facciamoci aiutare dalla seguente tabella, presa dall’articolo [7], che sarà d’ora in poi il nostro riferimento principale:
La tabella ci dice già molte cose. Se ci riferiamo ad esempio all’isoterma 80°C (alla quale la “cottura”, come vedremo, è già operante), ci accorgiamo che i tempi relativi a gnocchi e patate sono paragonabili ai rispettivi tempi di cottura. Non è certo così per la pasta secca. Il fatto è che patate e gnocchi si cuociono utilizzando l’acqua che già contengono, mentre la pasta secca è… secca e richiede un processo di imbibizione la cui lentezza spiega la grande differenza dei tempi di cottura.
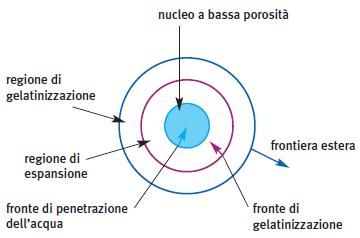
Trascuriamo qui l’abbassamento di temperatura dovuto all’immersione della pasta a temperatura ambiente (anche perché per il nostro esperimento bastano pochi spaghetti). Ora veniamo alla fase sperimentale vera e propria: ad ogni minuto dopo l’immersione estraete uno spaghetto ed esaminatelo. Per i primi cinque-sette minuti (dipende dal diametro) lo spaghetto si spezza, se piegato oltre un certo limite, ma dopo acquista una buona flessibilità. Se lo sezionate noterete che per i primi campioni esiste una vasta zona centrale biancastra circondata da un anello dall’apparenza più “morbida”. Lo spaghetto sta appunto cercando di mostrarvi il fenomeno importante in questa fase del processo: la penetrazione dell’acqua. Naturalmente questo si verifica per ogni tipo di pasta secca ed è tipico anche della cottura dei cereali (che però sono ancora più compatti e quindi richiedono più tempo). Nella geometria semplice dello spaghetto è però ben visibile il fronte circolare di penetrazione. Rimandiamo la domanda di come si potrà descrivere la dinamica di questo fronte e continuiamo l’esperimento sezionando spaghetti più “maturi”. Adesso vedremo che la zona interna si è molto ridotta e che compare un nuovo anello esterno dal colore avorio. Questa è la regione della pasta “cotta”.
Ma cosa vuol dire “cotta”? L’ingrediente dominante della pasta è l’amido. Questo è una grande invenzione delle piante, che lo accumulano nei tuberi o nei semi perché serva da nutriente per i germogli. Si tratta di un polisaccaride, cioè – per farla breve – un polimero costituito da una catena di molecole di glucosio.
Ma come – direte – la sintesi dei polimeri è stata una vittoria abbastanza recente della Chimica (che ci ha regalato ogni sorta di “plastica”) e invece le piante hanno sempre saputo come farla? Proprio così! Ma non solo le piante: la seta e la ragnatela sono polimeri con eccezionali proprietà meccaniche. Noi siamo ben pieni di polimeri (non siamo fatti di plastica, ma tutto ciò che abbiamo di fibroso – ad esempio “la trama” del tessuto connettivo – è di quella natura). Comunque cerchiamo di non perdere di vista la pasta. L’amido non è digeribile dall’uomo (almeno in una cosa siamo inferiori ai polli). Perché lo diventi, bisogna gelatinizzarlo. Vuol dire che la catena polimerica va spezzata in aggregati più semplici. Questo lavoro è affidato all’acqua che la attacca in più punti e la idrolizza. Il processo però avviene solo quando si raggiunge una sufficiente concentrazione di acqua (che dipende dalla temperatura, la quale per nostra fortuna è fissa). La presenza di una tale soglia spiega la comparsa del secondo fronte, che è appunto il fronte di gelatinizzazione.
Continuando a estrarre e sezionare spaghetti, si vede che i due fronti si muovono verso il centro.
Noterete che lo spaghetto “al dente” contiene ancora un piccolo nucleo non gelatinizzato (o addirittura non penetrato). Lo spaghetto “scotto” è semplicemente uno spaghetto cotto. Altro esperimento interessante: lasciate degli spaghetti crudi immersi in acqua fredda e andate a dormire. Il giorno dopo li troverete completamente molli. Segno che la temperatura influenza solo la velocità di penetrazione, ma il processo di imbibizione avviene anche a temperatura ambiente. Solo che ovviamente gli spaghetti non saranno cotti: avranno un disgustoso colore bianchiccio, invece del caldo color avorio della pasta cotta. Io non ho avuto il coraggio di assaggiarli (l’amore per la scienza ha i suoi limiti).
Ho cercato di ritardare il momento, ma dobbiamo finalmente affrontare il modello matematico. Come abbiamo visto, grazie alla particolare geometria dello spaghetto (per questo non abbiamo preso le farfalle o i tortiglioni) sarà sufficiente studiare il problema su una sezione trasversale generica e quindi con una sola coordinata spaziale: la distanza r dall’asse dello spaghetto. Due sono i processi da studiare: imbibizione e gelatinizzazione. A ciascuno di essi è associato un fronte, che indicheremo rispettivamente con:
Per quanto riguarda il primo, gli ingegneri alimentari (se possiamo definirli così) hanno preso a prestito un modello che è stato concepito per la penetrazione di solventi in polimeri vetrosi (inverecondo paragone). Tradotto per il nostro spaghetto, il modello dice due cose: 1) il meccanismo di trasporto dell’acqua è la diffusione; 2) la diffusività dell’acqua si mantiene molto bassa finché l’acqua non supera una certa concentrazione, oltre la quale aumenta esponenzialmente con la concentrazione stessa. Questo apparato matematico consente di realizzare una zona povera di acqua e una che si satura rapidamente, ma dobbiamo proprio fidarci? Sarebbe molto bello potersi dilungare sul concetto di diffusione, ma accontentiamoci di dire che l’equazione che solitamente si usa:
(c = concentrazione, D = diffusività) esprime la cosiddetta legge di Fick (peccato che non ci sia tempo di occuparsi di questo interessante personaggio: basti dire che era un medico), la quale è applicabile per soluzioni diluite. I nostri ingegneri hanno preso D = D(c) nel modo in cui ho detto perché effettivamente fa tornare le cose, ma dove sta la soluzione diluita? Non c’è un’altra maniera di far camminare l’acqua? Va bene, la pasta è un polimero ma è anche un mezzo poroso. E qual è la grandezza regina capace di spostare liquidi dentro un mezzo poroso? La capillarità – la grande forza che tira l’acqua fino alla cime di alberi altissimi – capace di creare notevolissimi gradienti di pressione. Ecco allora la prima idea: abbandonare la (1) e vedere se buoni risultati possono ottenersi partendo dall’ipotesi che sul fronte di penetrazione dell’acqua si crei una depressione di capillarità abbastanza grande da risucchiare efficacemente l’acqua all’interno. Poi dovremo dire come l’acqua si sposta tra le fibre di amido che gradualmente si aprono al suo passaggio, ma questo è un problema molto classico e non ci preoccupa.
Proviamo a mettere le cose in ordine e a descrivere la fase di imbibizione. Prima di tutto abbiamo stabilito che in questa fase abbiamo solo due componenti: l’amido e l’acqua. Se indichiamo con φ la frazione di volume dell’acqua (detta anche porosità) e con φs quella della componente solida, avremo:
Per andare avanti dobbiamo tener conto che, imbarcando acqua, lo spaghetto aumenta di volume. Perciò, insieme al fronte di penetrazione dell’acqua r = s(t), avremo un fronte di espansione (la superficie esterna) r = σ(t). Al tempo t = 0 (inizio della penetrazione) avremo chiaramente s = σ = R (raggio dello spaghetto). Nota che s’< 0, σ’> 0. La figura qui sotto aiuta a visualizzare l’evoluzione del sistema.
La relazione tra le due frontiere si deduce in base a un bilancio di massa globale. Accanto alle incognite φs e φ dobbiamo introdurre le velocità (radiali) delle due fasi che indichiamo rispettivamente con u(r, t) > 0, v(r, t) < 0 . Adesso possiamo scrivere il bilancio di massa locale delle due componenti:
che, insieme a (2), esprimono la complessiva incomprimibilità del sistema:
Una informazione essenziale nel processo di imbibizione è la velocità con cui si aprono le fibre di amido per far posto all’acqua. Questa si può esprimere nella forma:
scegliendo opportunamente la funzione di imbibizione F.
Questo è un punto delicato e ne faremo un breve cenno alla fine. Diciamo soltanto che F è una funzione C2, positiva e decrescente in un intervallo (0, φM), dove φM < 1 indica il valore massimo raggiungibile dalla frazione d’acqua (quello al quale inizierà la gelatinizzazione). Per quanto riguarda il moto dell’acqua attraverso le fibre di amido, la cosa più naturale è utilizzare la classica legge di Darcy (che ormai ha superato il secolo e mezzo di vita):
dove la grandezza k è detta conducibilità idraulica e p è la pressione dell’acqua. Dunque l’acqua si muove grazie al gradiente di pressione e questo è creato, come dicevamo, dalla pressione di capillarità sul fronte di penetrazione. Se diciamo che p = 0 è la pressione nella pentola (è solo una scelta della scala) e che –pc è la pressione di capillarità, allora le condizioni da imporre su p sono:
Inoltre notiamo che la superficie esterna è una superficie materiale, ossia possiede la velocità della componente solida:
Per chiudere (come si dice) il sistema, dobbiamo dire qualcosa in più sulle modalità di penetrazione perché la (6) si riferisce al processo di imbibizione dopo il passaggio del fronte. Trascurando la porosità della pasta secca (guardate bene la sezione dello spaghetto crudo), diciamo che la porosità salta dal valore zero a un valore positivo φW < φM. Avendo preso r = s(t) come una superficie materiale, è ovvio che:
Le equazioni scritte finora consentono di determinare tutte le grandezze incognite fino all’istante tM in cui f raggiunge il valore φM sulla frontiera esterna. Da questo istante abbiamo a che fare col fronte di gelatinizzazione r = h(t), che anch’esso procede dall’esterno, h(tM) = σ(tM), verso l’interno. Il processo di idrolisi implica che una parte dell’acqua venga immobilizzata. Quindi accanto alla frazione di acqua libera φ, dovremo considerare una frazione di acqua immobilizzata η. Tra l’una e l’altra, c’è una cinetica di transizione espressa da:
con G decrescente a zero per η tendente a un valore massimo ηM, che ci consente di riscrivere il bilancio delle due grandezze come segue:
(si noti che l’acqua legata si muove con la velocità della componente solida). Nella fase di gelatinizzazione, possiamo trascurare ogni ulteriore rigonfiamento del sistema, ponendo:
e ciò comporta
Adesso vediamo quante cose dobbiamo specificare sul fronte di gelatinizzazione. Anzitutto, esso è definito come la superficie di livello:
attraverso la quale le grandezze φS e u sono continue, mentre f subisce un salto dal valore φM ad uno inferiore fM – h0 (parte della gelatinizzazione avviene istantaneamente). La discontinuità di φ produce una discontinuità della velocità v. Trafficando un po’ con i bilanci di massa, si arriva a scrivere la seguente equazione:
che tradotta in parole significa che lo spostamento del fronte porta una perdita di acqua libera e questa è la differenza tra il flusso d’acqua libera prima e dopo il fronte. Insieme alla (16), utilizzando nuovamente la legge di Darcy, possiamo scrivere:
dove la parentesi quadrata indica il salto della velocità dell’acqua libera relativa a quella legata attraverso il fronte, dovuto all’immobilizzazione dell’acqua che accompagna il moto relativo del fronte rispetto all’amido (secondo membro). Ancora una volta l’informazione sulla frontiera esterna proviene da un bilancio di massa globale.
Se adesso pensate che siamo vicini alla fine, vi sbagliate di grosso perché la matassa si è molto aggrovigliata e bisogna trovare il modo di sbrogliarla. In termini matematici vuol dire dimostrare un teorema di esistenza e unicità. Niente paura, ma la dimostrazione è piuttosto corposa [7].
Allora cerchiamo di riempire solo qualche spazio vuoto. La lacuna più grossa riguarda la funzione F(φ), che specifica la cinetica di imbibizione. La sua scelta è veramente delicata ed è ampiamente discussa in [7]. Una scelta ragionevole è del tipo A(φ* – φ)n , con A e φ* costanti. Si vede allora che l’esponente n non può essere troppo piccolo perché altrimenti ci sarebbe una richiesta di acqua così eccessiva da richiedere a un certo punto una regressione del fronte di imbibizione, cosa che non è assolutamente osservata nello spaghetto. Non mi dilungo ulteriormente. È interessante osservare che è possibile calcolare “a mano” il comportamento del fronte durante i primi minuti, che risulta essere del tipo
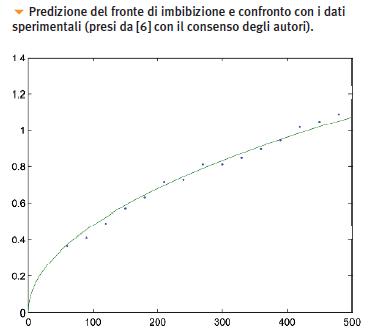
Forse vi eravate affezionati, ma è arrivato il momento di chiudere. Non prima però di aver mostrato il confronto coi dati sperimentali della fase di imbibizione:
Mica male no? D’ora in poi penso che, quando avrete davanti un bel piatto di spaghetti, non potrete più evitare di pensare a quanta Matematica c’è dentro e spero che ciò ve li renda più gustosi. Buon appetito!
Bibliografia
[1] E. Giusti, La Matematica in Cucina, Bollati Boringhieri, 2004, Torino.
[2] P. Sadd, D. Jefferson, A. Lacey, “Crust density in bread baking: mathematical modelling and numerical solutions”, App. Math. Modelling, 31, 2007.
[3] A. Fasano, A. Mancini, “Modelling the onset of vaporization in frying processes with no mechanical deformation”, J. Food Process Engineering, 33, 2010, DOI: 10.1111/j.1745-4530.2008.00278.x
[4] A. Fasano, A. Mancini, “Math from the pan: fantastic voyage through a French fry”, SIAM News, maggio 2008.
[5] A. Fasano, A. Mancini, “A phenomenon of waiting time in phase change problems driven by radiative heat transfer”, Math. Meth. Appl. Sci., 32, 2009.
[6] A. Fasano, A. Mancini, M. Primicerio, B. Zaltzman, “Waiting time phenomena forced by critical boundary conditions in classical diffusion problems”, Quart. Appl. Math., 69, 2011.
[7] A. Fasano, M. Primicerio, A. Tesi, “A mathematical model for spaghetti cooking with free boundaries”, Appl. Math. J.: Networks and Heterogeneous Media, 6, 2011, pp.37-60.
[8] S. Cafieri, S. Chillo, M. Mastromatteo, N. Suriano, M.A. Del Nobile, “A mathematical model to predict the effect of shape on pasta hydration kinetic during cooking and overcooking”, Journal of Cereal Science, 48, 2008, pp. 857-862.