Michail Botvinnik: un programma "intelligente" per giocare a scacchi

Michail Botvinnik è stato campione mondiale di scacchi dal 1948 al 1963. Il suo lavoro - quello di cui parleremo ora - è stato finalizzato allo sviluppo di un programma per computer che imiti il modo di operare scelte dei grandi maestri di scacchi.

Proprio per tale suo impegno di ricerca, che ha condotto alla realizzazione di un programma chiamato Pioniere, l'Università di Ferrara ha conferito a Botvinnik, il 7 settembre 1991, la laurea ad honorem in Matematica.

Per inquadrare la sua ricerca nella giusta prospettiva occorre descrivere dapprima lo schema teorico di un programma di tipo standard. A tale scopo partirò un po' da lontano e, precisamente, da un risultato ottenuto nel 1913 dal matematico tedesco Ernst Zermelo.

Indice

1. L'algoritmo di analisi a ritroso di Zermelo

2. Turing e Shannon: utilizzo dell'analisi a ritroso e del metodo del minimax su un albero troncato

3. Il lavoro di Botvinnik per realizzare un programma intelligente

Riferimenti bibliografici

1. L'algoritmo di analisi a ritroso di Zermelo.

Il gioco degli scacchi è un gioco di strategia con mosse alternate di due giocatori, che può terminare con la vittoria del Bianco (il giocatore che ha la prima mossa) oppure con la vittoria del Nero oppure con la Patta. Esso è un gioco “a somma zero” poiché la vittoria dell'un giocatore è la sconfitta dell'altro.

Ernst Zermelo

Il grande matematico tedesco Ernst Zermelo si pose, nel 1912, il problema di provare che il gioco degli scacchi è strettamente determinato ossia che vale una di queste tre alternative:

• il Bianco ha a disposizione una strategia, cioè un piano completo di azione, che porta alla vittoria qualunque strategia adotti il Nero;

• il Nero ha a disposizione una strategia, che porta alla vittoria (del Nero) qualunque strategia adotti il Bianco;

• sia il Bianco sia il Nero hanno a disposizione ciascuno una strategia che assicura almeno la patta qualunque cosa faccia l'altro.

Effettivamente egli riuscì a dimostrare questo risultato in un suo lavoro (“Uber eine Anwendung der Mengenlehre auf die Theorie des Schachspiels”) pubblicato nel 1913, utilizzando un algoritmo di analisi a ritroso, la cui logica è illustrata nel banale esempio rappresentato graficamente dall'albero seguente:

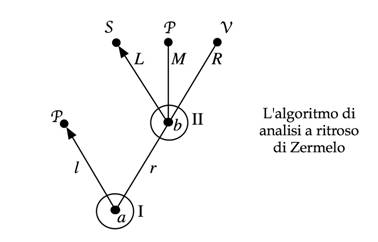
Nello stato iniziale cioè nel nodo a ha la mossa I (Primo) che può scegliere tra due azioni (“mosse”) l ed r . Se I sceglie l si arriva ad un nodo terminale contrassegnato P (=patta) cioè la partita termina subito ed è patta. Se I sceglie r si arriva ad un nodo b , in cui la mossa spetta a II che può scegliere fra tre azioni L , M , R che portano tutte a nodi terminali cioè alla conclusione del gioco. Se II sceglie L la partita termina con l'esito S , che significa sconfitta del Bianco e vittoria del Nero; se sceglie M la partita termina con l'esito di patta; se sceglie R , la partita termina con l'esito V , che significa vittoria del Bianco e sconfitta del Nero. Naturalmente si suppone che I preferisca l'esito V ad ogni altro e l'esito P all'esito S , mentre le preferenze di II sono opposte ossia II preferisce nell'ordine S, P, V. In parole povere, ciascuno gioca per vincere.

Mostriamo come funziona l'algoritmo di Zermelo nel nostro esempio. Partiamo dal nodo prefinale b (nodo che dopo di sé ha solo degli esiti): II, se è razionale, sceglie l'azione L che dà l'esito S (vittoria di II). Allora I, conscio di questo fatto, deve sostituire mentalmente il sottogioco che parte dal nodo b con l'esito S , e dunque I, nel nodo iniziale a (“radice“ dell'albero), sceglie l che porta all'esito P . In conclusione I sceglierà la “strategia” l , II pianificherà di giocare L se avrà la mossa, e il “valore” del gioco G è P . (Nella figura le frecce evidenziano le scelte di I e di II.)

L'albero degli scacchi, come vedremo tra poco, è terribilmente grande, ma ha pur sempre un numero finito di nodi ed allora potendo realmente usare il procedimento di analisi a ritroso illustrato nell'esempio e detto ora “algoritmo di Zermelo”, si arriverebbe a decidere qual è il valore del gioco degli scacchi e a determinare una strategia ottimale del Bianco e una strategia ottimale del Nero. Ciò peraltro, se fosse realizzabile, toglierebbe ogni interesse al gioco. Ma la grandezza dell'albero degli scacchi è tale che anche il più potente dei computer attuali impiegherebbe miliardi di miliardi di miliardi di anni per compiere una tale analisi.

Per convincerci di questo basta un semplice calcoletto. Nella sua posizione iniziale il Bianco ha 20 scelte possibili e per ciascuna mossa iniziale del Bianco il Nero ha 20 risposte possibili. Andando avanti il numero delle possibili scelte a disposizione aumenta. Tuttavia, proviamo a ragionare come se tutte le possibili partite terminassero dopo solo 20 mosse del Bianco e 20 mosse del Nero, per un totale di 40 mosse e supponendo che ogni volta che muove ciascuno abbia a disposizione 20 scelte possibili. Il numero dei nodi compresi quelli terminali dell'albero che rappresenta un tale gioco è allora

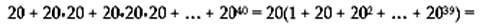
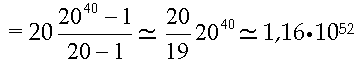
Solo per decidere la prima mossa del Bianco il computer deve costruire l'albero e poi ripercorrerlo a ritroso. Ora un computer che visiti 10¹⁰ nodi al secondo in un anno (non bisestile)  impiegherebbe un tempo dell'ordine di grandezza di

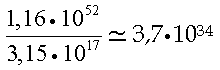
anni per percorrere una sola volta un tale alberello (molto, molto più piccolo del vero albero degli scacchi).

2. Turing e Shannon: utilizzo dell'analisi a ritroso e del metodo del minimax su un albero troncato.

L'utilizzo effettivo degli elaboratori come strumento di calcolo iniziò, come noto, verso la fine della seconda guerra mondiale. Il grande matematico e logico inglese Alan Turing, intravvide ben presto, e cioè nel 1947, la possibilità di programmare il computer per giocare a scacchi.

Alan Turing

Egli era un appassionato del gioco degli scacchi anche se il suo livello di gioco era modesto. A tale proposito si può ricordare un gustoso aneddoto riportato nella sua biografia (A. Hodges, Storia di un Enigma , Bollati Boringhieri). A Bletchey Park dove lavorava, durante la seconda guerra mondiale, alla decodificazione dei messaggi cifrati dei sottomarini tedeschi, egli era circondato da alcuni maestri di scacchi, tra cui il più volte campione di Gran Bretagna Harry Golombek. Golombek raccontò (sull'Observer Magazine del 7 novembre 1976) che nel corso di una partita con Turing, avendo questi deciso di abbandonare, gli propose di continuare scambiando le parti. E Golombek riuscì a vincere facilmente (a suo dire) col colore con cui Turing aveva deciso l'abbandono.

Harry Golombek

Comunque, anche senza essere un colosso della scacchiera, Turing riuscì a scrivere un programma per giocare a scacchi che poi utilizzò in alcune partite, in cui peraltro simulò il programma con calcoli fatti a mano, stante la lentezza degli elaboratori del tempo e forse la difficoltà di averne uno a disposizione per giocare.

Lo schema di base del programma di Turing è una procedura di tipo minimax diventata poi standard col nome di schema di Turing-Shannon e che può essere descritta in questi termini:

• In ogni posizione della partita viene considerato non l'albero del gioco (stante l'impossibilità pratica di usare su di esso l'algoritmo di Zermelo) bensì un albero ottenuto troncando l'albero reale ad una profondità fissata d (la profondità è il numero di mosse con cui viene portata avanti ogni continuazione).

• Viene definita una funzione di valutazione euristica che permette di assegnare ad ogni posizione un punteggio (un numero reale), riferito convenzionalmente al Bianco, che rappresenta una stima della posizione. Possiamo porre uguale a zero una stima di “posizione pari” sicché un numero positivo indica un vantaggio del Bianco e un numero negativo un vantaggio del Nero.

• In ciascun nodo x il programma opera la scelta del giocatore che deve muovere, usando l'algoritmo (generalizzato) di analisi a ritroso di Zermelo sull'albero troncato di radice x e profondità d . Ossia, si procede a ritroso su tale albero, partendo dai nodi prefinali e supponendo che in ogni nodo del Bianco egli scelga un'azione che massimizzi la funzione di valutazione e che in ogni nodo del Nero, egli scelga un'azione che minimizzi la funzione di valutazione.

Il funzionamento del meccanismo è illustrato nella figura seguente:

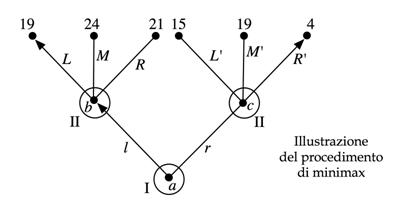
Cominciamo l'analisi a ritroso partendo dai nodi prefinali b e c . In b , II (che vuole minimizzare) sceglie L con valutazione 19 ed in c , II sceglie R ' con valutazione 4. Perciò I (che vuole massimizzare) nella mossa iniziale del gioco, cioè nella “radice” a dell'albero, sceglie l che lo porta in b , con valutazione 19. (Le frecce evidenziano le scelte ottimali di I e di II.)

Qualche anno dopo i primi esperimenti di Turing, il matematico americano Claude Shannon pubblicò un saggio (“ Programming a computer for playing chess, Phil. Mag. 41, 1950) in cui egli svolge un'analisi teorica dettagliata dei vari aspetti che intervengono nella realizzazione effettiva di un programma che utilizza il procedimento di minimax.

Claude Shannon

In un primo approccio (ne seguirà un secondo a cui accennerò nel paragrafo seguente) che riguarda appunto lo schema di Turing-Shannon descritto in precedenza, egli iniziò prendendo in considerazione gli aspetti tecnici che riguardano il modo di definire, nel programma, una generica posizione del gioco degli scacchi (benché questo appaia un aspetto secondario, solo nel 1958 apparve un programma che rispettava, in modo completo, le regole del gioco). Egli suggerì poi l'uso di una funzione di valutazione approssimata costituita di due termini additivi. Il primo termine è un punteggio che rappresenta la differenza di materiale tra i due eserciti. Shannon adotta i seguenti valori per i pezzi: Pedone 1, Cavallo 3, Alfiere 3, Torre 5, Regina 9, Re 200 (naturalmente il valore del Re, negli scacchi, è infinito e 200 è solo un numero alto, che viene preso per motivi pratici di calcolo). Il secondo termine vuole rappresentare una valutazione del vantaggio (numero positivo) o dello svantaggio (numero negativo) posizionale del Bianco rispetto al Nero ed è costituito da una combinazione lineare di vari fattori ben noti ai giocatori di scacchi (per esempio, un avamposto di Cavallo).

Shannon segnalò anche la possibilità di immettere nella memoria dell'elaboratore un libro di aperture, ciò che dal 1970 in poi è divenuto un fatto di routine in tutti i programmi in uso; chiunque abbia giocato contro il computer sa che, nella fase iniziale della partita, la risposta della macchina è istantanea, poiché in realtà essa si limita a leggere la mossa nel libro delle aperture. Egli suggerì inoltre di introdurre nel programma la possibilità di scelte aleatorie (tra mosse suggerite dalla teoria degli scacchi) per evitare la ripetizione della stessa partita.

Non molto dopo la pubblicazione del saggio di Shannon fu scoperto un importante mezzo per aumentare la profondità dell'analisi e cioè la potatura a - b dell'albero delle varianti, che permette di analizzare, anziché l'intero albero troncato, un suo sottoalbero proprio. L'idea è illustrata nell'esempio seguente, in cui, al solito, I (il Bianco) vuole massimizzare, mentre II (il Nero) vuole minimizzare.

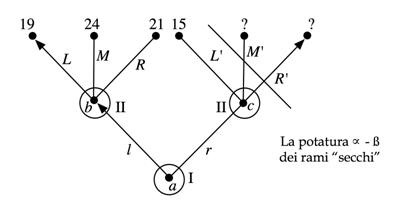
Cominciamo l'analisi a ritroso nel nodo prefinale b , In b , II (che minimizza) sceglie la mossa L che determina il valore 19. Passiamo a considerare il nodo c . In c una volta visto che la mossa L ' porta al valore 15 diventa inutile esaminare i rami M ' ed R ' che possono solo abbassare il valore che sarà ottenuto dalla scelta di II in c . Infatti, a questo punto, è certo che I, che vuole massimizzare, sceglierà l e non r nel nodo a . Perciò potiamo i rami M ' ed R '.

Tale sistema di potatura (dei rami “secchi”), nelle situazioni più favorevoli, permette di ridurre il numero dei nodi da esaminare da n a 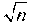. Non è cosa da poco: se, a titolo di esempio, nella posizione iniziale degli scacchi consideriamo un albero con 6 livelli (tre mosse del Bianco e tre mosse del Nero) e supponiamo che ad ogni mossa ciascuno abbia 20 alternative allora il numero dei nodi da esaminare sarebbe

n=20+20² + ... +20⁶=(20/19)(20⁶-1)=67 368 420

ma tale numero si può ridurre (se l'ordine in cui esaminiamo i nodi è azzeccato) a circa

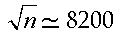
Il primo programma di una certa forza, tra quelli che seguono lo schema standard di Turing-Shannon completato con la potatura dell'albero, fu un programma realizzato tra il 1961 ed il 1966 da un gruppo di fisici dell'Università di Mosca diretti da Adelson-Velsky e Arlazarov. L'evoluzione del loro programma portò alla realizzazione di Kaissa, vincitrice nel 1974 del primo campionato del mondo di scacchi per elaboratori. In seguito l'aumento vertiginoso della potenza degli elaboratori, il raffinamento degli algoritmi di potatura e l'immissione nel programma di grossi e perfezionati manuali sulle aperture sono i fattori che hanno fatto aumentare enormemente il rendimento finale dei programmi che seguono lo schema di Turing-Shannon.

Ma ora è tempo di parlare di un diverso modo di affrontare il problema, a cui ha dato un impulso notevole il lavoro di Botvinnik.

3. Il lavoro di Botvinnik per realizzare un programma intelligente.

Per illustrare le idee alla base del programma realizzato da Michail Botvinnik tra il 1965 ed il 1980, conviene partire un po' più indietro nel tempo. Negli anni '40 lo psicologo olandese Adrian de Groot studiò la percezione che in una data situazione della scacchiera hanno da una parte i principianti e dall'altra i maestri di scacchi. I suoi risultati indicano che il maestro di scacchi percepisce la posizione dei pezzi in blocchi. Egli si costruisce dei livelli di organizzazione superiore sul modo di percepire la scacchiera; di conseguenza gli risulta naturale non considerare le mosse “cattive”. Ciò si può considerare una “potatura implicita” dell'albero del gioco, a differenza della potatura esplicita realizzata sull'albero troncato con l'algoritmo a - b , di cui ho parlato nel paragrafo precedente. Afferma Douglas Hofstadter in “Gödel, Escher, Bach: Un'Eterna Ghirlanda Brillante”: «il suo (del maestro) modo di percepire la scacchiera è un filtro: quando osserva la situazione di una partita, il maestro letteralmente non vede le mosse cattive, proprio come un dilettante non vede le mosse illecite…».

Anche Shannon, nel suo saggio del 1950, oltre a formalizzare la procedura standard (cioè lo schema di Turing-Shannon) aveva proposto una seconda e più sofisticata procedura in cui alcune continuazioni forti devono essere portate avanti il più possibile, mentre altre continuazioni non sono analizzate affatto. Shannon presenta questa proposta come una variante dello schema standard.

Botvinnik si muove in questa direzione ma in un modo molto più radicale. Innanzitutto egli si preoccupa di definire il quadro teorico in cui impostare il problema. Nel problema originale, quello cioè della risoluzione del gioco degli scacchi, ciascuno di due giocatori ha uno scopo ben preciso: dare scacco matto all'esercito avversario. Occorre, secondo Botvinnik, introdurre uno scopo anche nel problema approssimato espresso dall'uso (in ogni posizione) di un sottoalbero del gioco e lo scopo nel modello di Botvinnik non è più quello di dare scacco matto bensì quello, più prosaico, di guadagnare materiale. Per realizzare tale scopo anche Botvinnik utilizza la procedura minimax ed una funzione di valutazione della posizione analoga a quella suggerita da Shannon e cioè costituita di due termini additivi relativi l'uno alla valutazione materiale dei pezzi sulla scacchiera (egli adotta per i pezzi gli stessi valori di Shannon) e l'altro alla posizione. Lo scacco matto è visto nel suo modello come caso particolare di guadagno di materiale (il Re è valutato 200 e cioè molto di più dell'insieme di tutti gli altri pezzi). Anch'egli adotta poi alcuni accorgimenti, quali l'utilizzo di un libro di aperture e di una piccola biblioteca di finali.

Ciò che differenzia il programma di Botvinnik dallo schema di Turing-Shannon è la costruzione dell'albero utilizzato nel suo modello. Botvinnik costruisce nel suo programma, in ogni posizione della partita, un albero lungo e stretto che non è ottenuto con la troncatura ad un livello fissato e la potatura meccanica dell'albero reale del gioco bensì con la costruzione di un sottoalbero, con “orizzonte” variabile, in cui solo i rami “più vigorosi” sono presi in considerazione.

Per realizzare tale idea programmatica, egli utilizza alcuni principi per la limitazione dell'analisi e un complesso modello matematico. Gli ingredienti essenziali del modello matematico di Botvinnik sono l'orizzonte limite variabile (in ogni posizione, il numero massimo di mosse che può venir preso in considerazione) e l'”albero delle traiettorie” che rappresenta un insieme di azioni e obiettivi ammissibili. L'albero delle traiettorie è costituito formalmente da quei pezzi che, nei limiti dell'orizzonte, sono in grado di partecipare alle azioni prese in considerazione e dall'insieme delle case che essi possono attraversare. Questa schematizzazione è conforme al modo di operare scelte del maestro di scacchi: egli inizia calcolando le possibilità di attacco (e di difesa) entro i limiti dell'orizzonte e non vede tutti i pezzi ma solo quelli che intervengono nei suoi calcoli e quella parte delle case della scacchiera che tali pezzi attraversano. La complessità del modello matematico di Botvinnik (che viene descritto nella sua monografia del 1982, Computers in Chess ) deriva dal fatto che la determinazione dell'orizzonte e quella degli obiettivi ammissibili sono reciprocamente dipendenti, come le incognite di un sistema di equazioni.

Il programma di Botvinnik non ha preso parte ai tornei per elaboratori per cui è difficile dare un giudizio sulla sua forza di gioco. Si ritiene peraltro, in base ai test di laboratorio effettuati, che esso abbia grandi capacità di affrontare situazioni strategicamente complesse.

Come ricordava Odifreddi, nell'articolo citato all'inizio, il test più significativo tra quelli noti è stato la risoluzione nel 1977 del difficile studio di Nadareisvili descritto di seguito e che il programma Chess 4.6, vincitore nel 1977 del secondo campionato del mondo di scacchi per elaboratori, fu incapace di risolvere.

La posizione dello studio di Nadareisvili, riportata nella figura che segue, è, nell'usuale notazione algebrica per la scacchiera,

G. Nadareisvili. Il Bianco, col tratto, vince.

Bianco: Rh8, Pe3, Pg5, Ph5

Nero: Rf5, Ac2, Ce1, Pc7, Pc5, Pe6

La variante fondamentale scoperta da Pioniere inizia con le mosse

1. Pg6 Rf6

2. Pg7 Ah7!

3. Pe4!! …

[Non 3. Rxh7 Cf3! 4. Pg8-D Cg5+ che porta alla patta.]

e ora dopo 3. … Cf3 4. Pe5+ Cxe5 5. Rxh7 Cf7 6. Pg8-D Cg5+ 7. Dxg5+ Rxg5 8. Ph6 Pc4 lascio al lettore, che sia ferrato scacchisticamente, il compito di verificare che, nella posizione ottenuta, il Bianco vince facilmente.

La logica dello studio di Nadareisvili consiste essenzialmente nel fatto che il re nero, nella casa f6, controlla la casa di fuga del re bianco; questo dà controgioco al Nero.

È difficilissimo costruire un albero delle varianti profondo e stretto (ossia di tipo umano) senza la comprensione di questo fatto. L'impegno del Bianco deve perciò essere dedicato in parte a cacciare via dalla casa f6 il re nero: il successo di Pioniere nel condurre a termine un tale impegno, pur con una macchina di potenza assai modesta, ne evidenzia le caratteristiche di programma “intelligente”.

Il lettore che sia esperto di Scacchi e Computer potrà forse verificare che un qualche programma, in suo possesso, è in grado di risolvere agevolmente lo studio di Nadareisvili. Ma… attenzione! Occorre tener conto che i programmi attuali vengono fatti girare su macchine centinaia di volte più potenti di quelle del 1977, che essi posseggono grandi biblioteche non solo sulle aperture ma anche sui finali e sulle combinazioni, ed infine che i migliori di essi hanno recepito (almeno in parte) i suggerimenti di Shannon e di Botvinnik per ottimizzare la costruzione e la potatura dell'albero, nonché l'idea (di Botvinnik) di “inseguire”, nel finale, le posizioni vincenti riportate nella biblioteca dei finali.

Riferimenti bibliografici

Binmore K., Fun and Games (A Text on Game Theory) , D.C. Heath, 1992

Botvinnik M.M., Computers in Chess , Springer Verlag, 1982

Botvinnik M.M., Lavori critici e analitici 1928-1986: Memorie , Mosca, 1987 (in russo)

Hodges A., Storia di un Enigma (Vita di Alan Turing) , Bollati Boringhieri, 1991

Hofstadter D.R., Gödel, Escher, Bach: Un'Eterna Ghirlanda Brillante , Adelphi, Milano, 1986

Newborn M.M., Recent Progress in Computer Chess , Advances in Computer, Vol. 18, Acad. Press, 1979

Tomasi D., Origini ed Evoluzione dei Programmi per elaboratori che giocano a scacchi , Tesi di laurea in Matematica, Univ. di Ferrara, 1995