In obscurum coni conduxit acumen (ovvero l'infinito in un punto)

In obscurum coni conduxit acumen (ovvero l’infinito in un punto)

Il suggestivo titolo di questo articolo si riferisce alla prima descrizione del punto di fuga che sia giunta fino a noi. Si tratta di un verso di Lucrezio, il grande divulgatore scientiﬁco dell’antichità, che nel suo De rerum natura descrive la visione di un portico che si estende davanti a noi in profondità e che “congiunge tetto e suolo, tutto ciò che sta a destra e a sinistra, ﬁno a terminare nella punta oscura di un cono”. Questa punta oscura dove gli oggetti inﬁnitamente lontani si confondono gli uni agli altri e paiono raggrupparsi in un unico punto, questa illusione della visione che il pittore concretizza disegnando un punto, un punto di fuga, fa parte della grande eredità che ci proviene dal mondo classico. I versi di Lucrezio riecheggiano teoremi più antichi di almeno due secoli e raccontano una Matematica la cui essenza metodologica era ormai perduta.

Leggiamo nell’Ottica di Euclide gli stessi concetti in forma di teoremi:

Tra i piani che giacciono sotto l’occhio quelli più lontani appaiono più in alto.
Tra i piani che stanno sopra l’occhio quelli più lontani appaiono più in basso.
Tra i piani che si estendono longitudinalmente, quelli a destra sembrano deviare verso sinistra, quelli a sinistra verso destra.

La differenza è che ora questi fatti, che possono apparire la semplice trascrizione di fenomeni empirici molto comuni, sono inseriti all’interno di una teoria scientiﬁca che abbiamo chiamato la “geometria della visione diretta”[1], dato che oggi il termine Ottica ha assunto tutt’altro signiﬁcato. Questa teoria si basa su premesse che ﬁssano gli enti teorici iniziali e le loro reciproche relazioni. È a partire da tali premesse, attraverso il ricorso alla Logica formale, al calcolo e a elementi di Geometria, che si dimostrano una serie di teoremi (sono 56 nell’Ottica di Euclide). Gli enti teorici fondamentali sono il raggio visivo che esce dall’occhio e raggiunge in linea retta la cosa vista e che permette di considerare il cono visivo (formato dai raggi che escono dall’occhio – vertice del cono – e colgono le cose viste) e l’angolo visivo la cui grandezza misura, quantitativamente, la grandezza apparente degli oggetti visti. In questo modo la grandezza reale di un segmento è data dalla sua lunghezza, mentre la grandezza apparente è data dall’angolo formato dai due raggi visivi che colgono le estremità del segmento. Le premesse stabiliscono che cosa voglia dire vedere più o meno grande, più o meno in alto (o in basso) e più o meno a destra (o a sinistra) un dato oggetto dello spazio. L’insieme di queste premesse stabilisce, in sostanza, che punti sullo stesso raggio visivo sono visti nello stesso modo.

Questa impalcatura molto semplice permette di geometrizzare la visione diretta, dimostrare teoremi e inventare esercizi di grande interesse anche dal punto di vista didattico. Naturalmente questa semplicità ha un prezzo: nell’Ottica euclidea si fa astrazione del fatto che la visione è bioculare e non monoculare, che l’occhio si muove e non è ﬁsso, che la ricostruzione cerebrale dell’immagine visiva è tutt’altro che oggettiva, che i raggi visivi in realtà non esistono ma esistono dei raggi di luce riﬂessi nella retina dall’oggetto visto, ed altro ancora. La cosa tuttavia sorprendente – e in questo sta la genialità di questa teoria – è che, malgrado le astrazioni fatte e l’estrema semplicità geometrica, le sue conseguenze applicative sia in relazione alla pittura che alla scenograﬁa o alla Geograﬁa astronomica sono molto efﬁcaci. Oggi possiamo capire facilmente il motivo di questi successi pensando che, in un certo senso, Euclide descrive (con le sue premesse e i suoi teoremi) la resa di una macchina fotograﬁca. Di tutti i teoremi dell’Ottica euclidea soffermiamoci in modo particolare sul teorema 6 che afferma testualmente:

“Segmenti paralleli visti da lontano appaiono non paralleli”.

Questa affermazione appare come l’ovvia trascrizione di una comunissima esperienza che si ricava quando, ad esempio, guardiamo due ﬁlari di alberi paralleli o un sentiero rettilineo che si allontana da noi o, ancora, un colonnato. Tuttavia, se facciamo attenzione alla dimostrazione, essa ci appare meno banale. La dimostrazione si basa sulla considerazione del segmento di distanza: date due rette parallele a e b e un punto A sulla retta a, possiamo trovare un corrispondente punto B sulla retta b prendendo la perpendicolare ad a per A. Il segmento AB così costruito si chiama segmento di distanza. Quando A si muove sulla retta a allontanandosi dall’occhio, il segmento AB (che, essendo le rette parallele, ha sempre la stessa grandezza) allontanandosi dall’occhio insieme ad A, si vedrà per il teorema precedente (teorema 5) via via più piccolo. Quindi il punto B si vedrà avvicinarsi sempre di più da A, ﬁno a confondersi con lui al limite della risoluzione visiva.

Questa, che è in sostanza la dimostrazione euclidea, mantiene la sua validità con minime variazioni anche se le rette in questione sono più di due. Se abbiamo infatti una terza retta c parallela ad a, avremo in corrispondenza ad un punto A di a un segmento di distanza AB tra le rette a e b e un segmento di distanza AC tra le rette a e c. Man mano che A si allontana dall’occhio, per quanto detto, il punto B si vedrà avvicinarsi ad A ﬁno (al limite della risoluzione visiva) a confondersi con lui. Ugualmente il punto C si vedrà avvicinarsi ad A e al limite confondersi con lui di modo che, in deﬁnitiva, i tre punti A, B, C vengono visti convergere tra loro.

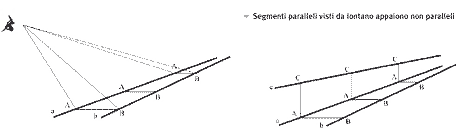
Ora, l’enunciato euclideo non precisa se, per segmenti paralleli, si debbano intendere due o più segmenti ma il fatto che la dimostrazione si riferisca al caso di due ha portato i vari commentatori dell’opera euclidea a considerare solo questo caso – confermato banalmente dall’esperienza empirica – senza osservare come lo stesso argomento dimostrativo sia valido per un numero arbitrario di segmenti, nel qual caso la cosa risulta tutt’altro che banale e difﬁcilmente desumibile dall’esperienza quotidiana. Sappiamo che nella Matematica ellenista esistevano diverse tipologie e stili: i teoremi erano enunciati dotati di una dimostrazione ottenuta sulla base della Logica aristotelica con un numero ﬁnito di passi; le costruzioni erano delle procedure attraverso le quali era possibile ottenere di fatto l’esistenza di opportune strutture; i porismi – la natura dei quali è tutt’oggi discussa – sembra che fossero una via di mezzo tra un teorema e una congettura veriﬁcabile solo in determinate ipotesi da precisare. Gli enunciati dell’Ottica che Euclide numera senza attribuir loro alcun nome, se vengono interpretati non come teoremi chiusi ma come la deﬁnizione di un contesto all’interno del quale esplicitare l’argomentazione rigorosa, offrono spunti di estremo interesse.

La geometria della visione di Euclide stabilisce chiaramente che segmenti paralleli che si estendono in profondità vengono visti convergere. Ciò signiﬁca che gli immaginari prolungamenti di questi segmenti si avvicinano sempre più tra loro, ﬁno a confondersi nella punta oscura di un cono. È chiaro il signiﬁcato prospettico di questo teorema: se si vuole che la visione di segmenti paralleli, rappresentati sul piano del quadro, sia uguale alla visione dei segmenti reali – come se il piano del quadro fosse un vetro sul quale si proietta la scena da rappresentare – si dovrà fare in modo che anche i segmenti rappresentati sul quadro siano visti convergere. Ma su un piano tre o più segmenti (non paralleli) sono visti convergere se e solo se sono convergenti. Il punto in cui tali segmenti convergono è ora ﬁsicamente presente sul quadro e rappresenta un punto che nella realtà non esiste ma che possiamo immaginare inﬁnitamente lontano nella direzione dei dati segmenti paralleli.

Nel caso particolare in cui le linee parallele siano ortogonali al quadro (linee dette anche di profondità), esse si vedono convergere verso un punto che sul quadro è rappresentato dalla proiezione ortogonale dell’occhio, punto noto con il nome di punto di fuga principale o, per dirla con Alberti, con il nome di punto centrico. La regola che tutte le linee di profondità si debbano rappresentare convergenti verso uno stesso punto è tutt’altro che ovvia e comunque difﬁcile da riconoscere a occhio quando i segmenti paralleli sono lontani tra loro, ad esempio alcuni sul sofﬁtto di una stanza ed altri sul pavimento.

Non è un caso che, in tutta la pittura medioevale, questa regola non venga mai rispettata. Siamo invece convinti che il teorema della geometria della visione, che afferma l’apparente convergenza di segmenti paralleli, fosse ben noto ai pittori greco-romani (a partire per lo meno dal terzo secolo avanti Cristo) e crediamo che, di conseguenza, fosse anche noto il suo riscontro nella pratica della pittura. Ciò non signiﬁca che essi l’abbiano applicato ovunque. Al contrario, la regola, specie in grandi affreschi, è – pensiamo consapevolmente – spesso disattesa per ottenere effetti estetici di natura diversa. Questa tesi non è condivisa da Panofski [2] che invece, anche sulla base delle poche pitture antiche disponibili all’epoca, sostiene l’ipotesi di una prospettiva antica “curva” come la superﬁcie retinica, nella quale segmenti paralleli tra loro convergono a due e due a punti diversi disposti lungo un asse verticale, formando uno schema tipo “lisca di pesce”. Pensiamo che oggi vi siano invece elementi sufﬁcienti per poter dipanare la questione in modo deﬁnitivo nella direzione contraria a quella indicata da Panofsky. Anche se l’Ottica di Euclide non è un manuale ad uso dei pittori, né ce ne sono pervenuti altri di questa natura, tuttavia riteniamo che la testimonianza di Vitruvio sia molto importante. Nei suoi 10 libri sull’Architettura, Vitruvio non solo parla di scenograﬁa nel senso di rappresentazione di un ediﬁcio secondo la sua immagine prospettica, mostrando sia la facciata che le pareti laterali, ma in un certo senso indica anche alcuni suggerimenti su come concretamente realizzare tali “scenograﬁe”. Riportiamo nel riquadro 2 i due passi di Vitruvio, per alcuni versi oscuri e sui quali si è molto dibattuto, essendo questa la testimonianza più importante rispetto al problema che vogliamo affrontare.

Il primo brano di non facile interpretazione, oltre ad indicare l’origine preeuclidea di questi studi, parla di un centro da ﬁssare in un punto determinato dal quale poi deriverebbe – non sappiamo come – l’intera costruzione prospettica. La possibilità, che parrebbe naturale, di interpretare questo centro come il punto di fuga principale è decisamente contestata da Panofsky e da vari altri autori. Nel passo successivo, dove Vitruvio tenta una deﬁnizione di scenograﬁa, il riferimento al circini centrum sarà fortemente usato da Panofsky proprio come argomentazione contro l'esistenza del punto di fuga perché non appare nessun legame plausibile tra un compasso e la proiezione dell'occhio sul piano della parete. La difﬁcoltà a interpretare questo passo, che ha suscitato moltissime polemiche, sta nel capire in che senso Vitruvio si riferisca alla convergenza di tutte le linee di riferimento al centro del compasso.

Tutto diventa chiaro se – come viene argomentato nella Nota di Catastini [3] – pensiamo al compasso non come un piccolo oggetto con due gambe e una punta scrivente con cui è possibile fare piccoli cerchi, ma piuttosto al compasso dell’architetto con il quale si disegnano le tracce degli archi o le piante circolari degli ediﬁci o grandi cerchi su una parete. Questo compasso ci appare come un chiodo ﬁssato sulla parete al quale è legata una corda: con la mano, si tiene un capo della corda e una punta scrivente che si fa girare tenendo tesa la corda in modo da descrivere un cerchio.

Un modo semplice dunque per far convergere un piccolo segmento verso il punto di fuga (magari lontano) è quello di ﬁssare un chiodo in questo punto ﬁsso e di tendere lo spago, ﬁno al segmento che si deve tracciare, tirare una riga di riferimento un po’ più lunga del segmento da disegnare e ripetere la procedura, con lo stesso spago per tutti gli altri segmenti che debbono convergere nel punto dato. Lo strumento per realizzare questo è proprio – come dice Vitruvio – il compasso (dell’architetto).

In particolare, l’esempio della Stanza delle maschere (scoperta al Palatino a Roma nel 1961 e datata intorno al 50 a.C) non lascia dubbi sull’uso del punto di fuga come unico punto di convergenza delle rette di profondità.

Vi sono infatti decine e decine di segmenti anche molto lontani tra loro (l’affresco è lungo circa 5 metri) che, se prolungati, convergono ad un unico punto. Pensiamo che l’affresco sia stato realizzato proprio piantando un chiodo nel punto di fuga e tirando con lo spago i vari segmenti. Ma se questo è vero, si dovrebbe ancora trovare una traccia sul muro: una stuccatura nel punto esatto dove convergono tutte le linee. Un sopraluogo che abbiamo effettuato nella Stanza delle maschere nel 2003 con vari esperti ha confermato la presenza di una irregolarità nel punto di fuga senza però, in mancanza di una radiograﬁa del muro, poter dare una prova certa e deﬁnitiva della presenza del chiodo. Tuttavia, analizzando da vicino l’affresco, abbiamo trovato un’altra prova che ci pare molto signiﬁcativa. Di alcuni segmenti è rimasta la traccia di un breve prolungamento, cosa che non avrebbe senso fare se non si sapesse a priori che i prolungamenti debbono tutti convergere al chiodo.

Una tale operazione non può che essere frutto di una costruzione geometrica rigorosa, le cui fondamenta si ritrovano nell’Ottica di Euclide ed erano forse note anche prima. Vitruvio descrive in modo, secondo noi molto chiaro, anche la tecnica di realizzazione di tali rappresentazioni basate sull’uso del compasso.

Una ulteriore conferma di questa accezione del termine centro del cerchio come punto di fuga lo troviamo nell’Alberti che per primo scrive un testo, il De Pictura, nel quale vengono esplicitate le regole geometriche della prospettiva. Il libro, redatto per i pittori, non contiene dimostrazioni matematiche ma fornisce delle regole, anche estetiche, per realizzare uno scorcio prospettico. In questo libro, viene introdotto in modo esplicito il punto di fuga principale: il punto nel quale si vedono concorrere tutte le rette ortogonali al piano del quadro. Alberti attribuisce a questo punto il nome di punto centrico, termine che usa anche per denotare il centro di una circonferenza [4]:

“Sarà circolo forma di superﬁcie quale una intera linea quasi come una ghirlanda l’avvolge; e se qui in mezzo sarà uno punto, qualunque linea da questo punto sino alla ghirlanda sarà d’una mensura all’altre equale, e questo punto in mezzo si chiama centrico”.

Dunque Alberti chiama punto centrico sia il centro di una circonferenza sia il punto di fuga principale riecheggiando la tradizione degli architetti e quella vitruviana in particolare, sicuramente più vicina a lui che a noi. Pensiamo che questa identiﬁcazione non sia un elemento di confusione tra due concetti nettamente distinti. È piuttosto un richiamare, con il nome di punto centrico, l’immagine del cono visivo il cui asse – che nel linguaggio albertiano è chiamato il razzo centrico – incontra il piano del quadro a lui ortogonale in un punto (il punto centrico) che è proprio il centro del circolo ottenuto intersecando il cono visivo col quadro.

Nei quindici secoli che separano La Stanza delle maschere dal De Pictura di Alberti, la barbarie, le guerre, le brutali devastazioni e i saccheggi hanno fatto terra bruciata di gran parte del sapere scientiﬁco antico. In questo terribile regresso della scienza, sono più le conoscenze perdute di quelle rimaste. In particolare, ciò che riguarda la prospettiva antica è quasi del tutto perduto, a parte il testo di Euclide e i pochi e sibillini frammenti di cui abbiamo parlato. La ricostruzione di questo sapere geometrico avviene per vie traverse ed indirette, ad opera soprattutto dei pittori che tornano ad indagare sul modo di rappresentare realisticamente la profondità spaziale. La Matematica verrà dopo, con Piero della Francesca, Danti, Commandino e Guidobaldo del Monte.

Gli scienziati arabi, ai quali dobbiamo il parziale recupero delle conoscenze greche, svilupperanno nel IX, X e XI secolo l’Ottica antica recuperando il testo di Tolomeo (oggi parzialmente perduto) e contribuendo in modo essenziale a dare a questa disciplina il suo carattere attuale. In particolare Ibn al-Haytham (965-1039), nella sua Ottica, prende in esame una serie di aspetti importanti nella teoria della visione di cui Euclide aveva fatto astrazione. Riconosce il ruolo della luce nel fenomeno della visione e quello del cervello nella ricostruzione psichica delle immagini. Analizza dettagliatamente la ﬁsiologia dell’occhio e produce una serie di esperimenti per veriﬁcare le sue ipotesi. Ibn al-Haytham critica decisamente l’Ottica euclidea, che considera sbagliata, e non riconosce il metodo e l’importanza del modello geometrico che (a prezzo di molte sempliﬁcazioni) Euclide riesce a costruire. Ibn al-Haytham è sospeso tra Fisiologia e Fisica, tra Geometria e Psicologia ed è teso alla ricerca della Verità mentre Euclide, più modestamente, elabora un modello geometrico sempliﬁcato della visione diretta che permette, proprio per questo, non solo di spiegare coerentemente alcuni fenomeni comuni sulla visione, ma anche di dare indicazioni precise per il disegno prospettico. C’è anche da dire che poco era l’interesse del mondo arabo per la pittura ﬁgurativa e non ci stupisce quindi che questo settore non sia stato da loro preso in considerazione. In deﬁnitiva quei pittori come Cimabue e Giotto che, sul ﬁnire del XIII secolo, si posero il problema di rappresentare lo spazio, poterono appoggiarsi solo al loro gusto estetico e alla loro pratica pittorica.

È forse nel cantiere della Basilica superiore di San Francesco ad Assisi, dove Cimabue e Giotto lavorano insieme, che nascono le prime sperimentazioni [5]. Nella rafﬁgurazione della Madonna sul trono, immagine molto diffusa nel Medio Evo, per dare il senso della profondità, il trono veniva solitamente rappresentato secondo una visione insieme frontale e obliqua, mostrando il lato laterale con parallelogrammi. Cimabue, per primo, rompe questa consuetudine e introduce un asse di simmetria centrale che dà al-l’insieme una maggiore compostezza e regolarità. L’introduzione di questa simmetria porta come conseguenza che i segmenti che si corrispondono nella simmetria, se prolungati, andranno (per ovvie ragioni geometriche) ad incontrarsi sull’asse di simmetria. È su questo schema e non tanto su una presunta struttura “a lisca di pesce” ereditata dagli antichi – come sostiene Panofsky – che Giotto imposta le sue prime sperimentazioni. È chiaro che l’attenzione del pittore è tutta rivolta solo ai sofﬁtti, elemento decorativo scelto per dare l’idea della profondità dell’ambiente senza armonizzare questo coi pavimenti. Anche è chiaro come in Giotto manchi l’idea uniﬁcante che tutte le linee di profondità convergano a uno stesso punto di fuga dove si congiunge tetto a suolo. Il pittore non dispone di uno schema geometrico globale ma riesce solo ad applicare localmente, per parti parziali del dipinto, l’apparente convergenza delle linee parallele (come si vede ad esempio nel suo affresco Pentecoste). Anche altri maestri come Duccio da Buoninsegna o i fratelli Lorenzetti cercheranno la soluzione al problema di come rappresentare la profondità, senza trovarla. Sarà il rinascimento scientiﬁco – il grande fervore al tempo stesso umanista e scientiﬁco – a riportare alla luce l’interesse per gli antichi testi. L’Ottica di Euclide viene editata manoscritta nel 1458 proprio a Borgo San Sepolcro dove è nato Piero della Francesca. Brunelleschi, Alberti, Leonardo da Vinci, e lo stesso Piero, daranno corpo a regole precise e geometricamente corrette per la rappresentazione prospettica. Si recupera l’impianto euclideo basato sui raggi visivi e sul cono visivo che ha come vertice l’occhio e come base i contorni della cosa vista. La prospettiva diventa di nuovo Matematica, diventa lo studio dell’intersezione di un determinato cono con il piano del quadro. Ogni ﬁgura si proietta a partire dall’occhio, con delle rette (i raggi visivi) su un piano. Il problema diventa un problema puramente geometrico e tutto diventa un capitolo di quello che Poncelet, il fondatore della moderna Geometria proiettiva, chiamerà la Teoria delle proiezioni centrali.

BIBLIOGRAFIA

[1] Catastini L., Ghione F., Le geometrie della visione, Springer, Milano, 2004.

[2] Panofsky E., La prospettiva come forma simbolica, Feltrinelli, Milano, 1961.

[3] Catastini L., “Il centro del compasso: considerazioni sulla prospettiva antica”, in Prospettiva e Geometria dello Spazio, Agorà edizioni, Torino, 2005, pp. 57-68.

[4] Alberti L. B., De pictura, Libro I, n.2.

[5] Gandolfo F., Ghione F., “Giotto e il punto di fuga”, in Giotto e il Trecento, Skira Editore, Milano, 2009, pp 365-378.

In obscurum coni conduxit acumen (ovvero l'infinito in un punto)

Franco Ghione

Laura Catastini