Per Piero
Quale luce aveva sedotto Piero? La luce dei fondi oro ancora in voga nel primo Quattrocento, abbagliante, e che inevitabilmente aveva condotto, qualche secolo più tardi, alla cecità anche Joseph Antoine Ferdinand Plateau per un eccesso di zelo sperimentale, avendo egli rivolto per qualche secondo in più lo sguardo verso il sole. Luce abbagliante, appunto, che nei dipinti di Piero è declinata in forma cristallina… trasparente, diffusa, analitica… oppure quella descritta nel Timeo da Platone:
"Prima di ogni altro organo gli Dei fabbricarono gli occhi, che portano la luce e li disposero in siffatto modo: di tutto quel fuoco che non può bruciare ma produce la mite luce del giorno, fecero in modo che esistesse un corpo. Il fuoco puro che sta dentro di noi ed è della stessa natura di questo fuoco del giorno, lo fecero scorrere liscio e denso dentro agli occhi…".
Alla mite luce del giorno, che illumina le apparenze, corrisponde, per Platone, il fuoco interiore, camera oscurata – ai tempi di Piero – da secoli di oblio delle conoscenze scientifiche e dove i primi bagliori di luce inizieranno a dipanarsi in un tortuoso percorso, irto di ostacoli.
Le accurate descrizioni naturalistiche dei pittori del Gotico internazionale, adatte per una tassonomia, non saranno più sufficienti, Piero dovrà conoscerne la quintessenza, il dodecaedro che Platone, ancora nel Timeo, abbina agli altri poliedri regolari coniugandoli ai quattro elementi naturali conosciuti. E allora Piero redigerà il trattato "De quinque corporibus regolaribus" e, in sintonia con il motto platonico sulla Geometria, rivolgerà lo sguardo a un trattato di Matematica pura: gli "Elementi" di Euclide. Testo mirabile anche per noi moderni, che ne apprezziamo la struttura logica: dalle nozioni primitive all'incommensurabilità tra lato e diagonale del quadrato, dal semplice al complesso. Un percorso attraverso il quale era stato organizzato il trattato euclideo e che generazioni di studiosi hanno, nei secoli, indagato e sezionato, evidenziando i punti deboli, ciò che era o non era di Euclide.
Ma i contemporanei di Piero non avevano certo il piglio filologico di noi moderni, gli "Elementi" erano una porta di accesso, la più immediata, alle conoscenze matematiche ed era allora secondario indagare, nel tumulto delle scoperte, se i due libri dedicati ai poliedri, il XIV e il XV, fossero di altri autori o se addirittura l'Euclide matematico venisse sovrapposto al filosofo di Megara.
Ancora nell'edizione curata da Niccolò Tartaglia, con una vocazione pedagogica essendo redatta in volgare, il trattato attribuito all'Euclide Megarense conteneva i due libri spuri.
Agli occhi dei contemporanei di Piero i poliedri platonici apparivano quindi all'apice del testo euclideo, il fine ultimo ed essendo organizzati attorno ad un punto dal quale tutte le parti hanno uguale distanza, punto generatore di simmetrie e che tutto governa, rappresentavano il simbolo stesso degli ideali rinascimentali.

Disegni dei cinque poliedri regolari, attribuiti a Leonardo da Vinci, nel De divina proportione di Luca Pacioli che include il trattato Libellus de quinque corporibus regularibus di Piero della Francesca
Quel punto si sdoppierà in epoca barocca, ma i poliedri avranno ancora una lunga storia segnata, nei suoi momenti più alti, dal modello con il quale Keplero affronta, in forma teorica, il tema delle distanze tra i pianeti allora conosciuti, indicandone i rapporti; nel teorema sui poliedri di Eulero e, in epoca più vicina a noi, dalle cupole geodetiche progettate da Richard Buckminster Fuller.
Sul "De prospectiva pingendi" di Piero molto è stato scritto ed è quasi paradossale che quel punto, ancora rinascimentale, il quale organizza la griglia prospettica e fissa l'immagine statica osservata correttamente ancora da un unico punto di vista, sia all'origine di una geometria delle trasformazioni, indipendente dal modello euclideo.
L'approccio allo studio della Geometria di Girard Desargues, rivolto ancora alla soluzione di problemi pratici, secondo l'indicazione data dall'autore stesso, condurrà alla sostituzione delle invarianti percettive della Prospettiva con quelle metriche, i Birapporti che sono alla base della Geometria proiettiva, percorso completato dal Programma di Erlangen di Felix Klein, che segna, nell'Ottocento, il punto più alto relativo al tema delle trasformazioni stesse.
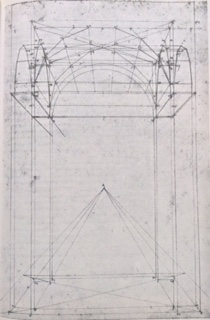
Tavola XIX, De prospectiva pingendi
Eppure il trattato di Piero pone quesiti ancora attuali sulla natura stessa della geometria, che proprio nell'Ottocento avevano generato una diatriba tra i fautori dei due indirizzi di ricerca seguiti: quello sintetico e quello analitico. Le frasi del trattato di Piero, che per noi contemporanei emanano un'ingenuità antica, segnalano invece in modo chiaro come le proprietà possano essere ricercate, in geometria, sia in forma astratta che applicata.
"Puncto è la cui parte non è, secondo i geometri dicono essere inmaginativo; la linea dicono avere lunghezza senza latitudine. Et perché questi non sono aparenti se non è a l'intellecto et io dico tractare de prospectiva con dimostrationi le quali voglio sieno comprese da l'ochio, perhò è necessario dare altra definizione. Dirò adunqua puncto essere una cosa tanto picholina quanto è posibile ad ochio comprendere…".
Piero della Francesca (biografia) Piero nacque a Borgo Sansepolcro, nell'attuale provincia di Arezzo, tra il 1406 e il 1416 (la data di nascita esatta è sconosciuta, poiché un incendio negli archivi comunali di Sansepolcro distrusse gli atti di nascita dell'antica anagrafe). Si formò a Firenze insieme a Domenico Veneziano con il quale collaborò per gli affreschi perduti del coro di S. Egidio a Firenze. Le prime opere, collocabili anteriormente al 1450, ci mostrano il personale carattere dell'artista: struttura prospettica rigorosissima, perfezione dei volumi geometrici, rappresentazione di figure grandiose immerse in un'atmosfera dalla luminosità diffusa, sottile e quasi astratta che mantiene i personaggi come sospesi nel tempo. Nel 1442 Piero ritornò a Borgo Sansepolcro dove fu candidato alle elezioni per la carica di consigliere popolare. Qui, la confraternita della Misericordia, gli commissionò un polittico che doveva essere consegnato entro tre anni, in realtà il pittore ne impiegò quindici per la creazione del Polittico della Misericordia, composto da 23 scomparti. Negli anni quaranta Piero soggiornò in varie corti italiane: Urbino, Ferrara e probabilmente Bologna. Intorno al 1451 il pittore si recò a Rimini dove lavorò nel Tempio Malatestiano all'affresco votivo col ritratto di Sigismondo Pandolfo Malatesta. Nel 1452, alla morte di Bicci di Lorenzo, Piero fu chiamato dalla famiglia Bacci per proseguire la decorazione del coro di S. Francesco ad Arezzo rappresentante la Leggenda della vera Croce. Tra il 1458 e il 1459 fu attivo a Roma, chiamato da papa Pio II. Presso il Palazzo Apostolico realizzò alcuni affreschi oggi andati perduti, dopo che nel XVI secolo vennero distrutti per far posto alla prima delle Stanze Vaticane di Raffaello. Nel biennio 1467-68 soggiornò a Perugia e Bastia Umbra, dove si era rifugiato per sfuggire la peste. Ospite, tra il 1469 e il 1472, presso la corte di Urbino di Federico da Montefeltro, produsse numerose opere tra le quali ricordiamo il Doppio ritratto dei duchi di Urbino, dove Federico da Montefeltro e la moglie Battista Sforza sono ritratti di profilo in primo piano. Negli ultimi anni, secondo il Vasari, venne colpito da una grave malattia agli occhi che lo costrinse a ritirarsi dalla sua attività, ma nello stesso periodo si applicò allo studio della prospettiva. Piero della Francesca morì a Sansepolcro il 12 ottobre 1492, proprio il giorno della scoperta dell'America. Oltre all'attività artistica Piero fu anche autore di trattati matematici e di geometria prospettica: il Trattato d'abaco, il De prospectiva pingendi e il De quinque corporibus regularibus. Piero, infatti, è considerato il matematico del Rinascimento; a lui si deve la formalizzazione delle regole che fino a quel momento erano patrimonio della sola tecnica artistica. La prima opera è stata il Trattato d'abaco, un manuale di calcolo scritto forse già nel 1450. La parte geometrica e algebrica risultano molto vaste rispetto alle consuetudini del suo tempo, così come la parte sperimentale. Nel De prospectiva pingendi, scritto quando ormai era già stato colpita dalla malattia, proseguì la sua linea di studio teorico codificando, per primo, le regole della moderna scienza prospettica. Nel terzo e ultimo trattato Libellus de quinque corporibus regularibus, dedicato alla geometria euclidea, riprese temi antichi di tradizione platonico-pitagorica; tra i problemi affrontati emergono il computo del volume della volta e l'elaborazione architettonica della costruzione delle cupole. Nel testo per la prima volta venivano disegnati i poliedri regolari e semiregolari, studiando le relazioni che intercorrono fra i cinque regolari. |

Piero della Francesca, Madonna del Parto, Museo della Madonna del Parto, Monterchi
PIERO DELLA FRANCESCA. Il disegno tra arte e scienza È il titolo della mostra che lo scorso 14 marzo si è inaugurata presso Palazzo Magnani a Reggio Emilia (dove resterà aperta fino al 14 giugno 2015), che presenta la figura del grande artista di Sansepolcro nella sua doppia veste di disegnatore e matematico. Per l'occasione sarà riunito – per la prima volta da mezzo millennio – l'intero corpus grafico e teorico di Piero della Francesca: i sette esemplari, tra latini e volgari, del De prospectiva pingendi, i due codici dell'Abaco e il Libellus de quinque corporibus regularibus. Un viaggio straordinario nel Rinascimento italiano, la cui unicità ha influenzato per secoli l'arte e il sapere del mondo intero, producendo i più grandi capolavori. Ad accompagnare i visitatori un'audioguida in cui il matematico Piergiorgio Odifreddi condurrà tra le opere grafiche e pittoriche di Piero e tra i capolavori pittorici e grafici di altri grandi maestri del XV e XVI secolo fra i quali Lorenzo Ghiberti, Domenico Ghirlandaio, Giovanni Bellini, Albrecht Dürer, Antonio da Sangallo il Giovane, Michelangelo.
Fulcro dell'esposizione è l'esemplare del De prospectiva pingendi della Biblioteca "Panizzi" di Reggio Emilia, il manoscritto, opera di un copista, reca numerose correzioni, note marginali ed estese aggiunte a mano di Piero che mostrano il lavoro di continua revisione del testo. Questo ospita, nei suoi 110 fogli, numerosi disegni a mano dell'artista. Le opere presenti in mostra accompagnano il visitatore in un percorso che segue a grandi linee le tematiche affrontate nei capitoli del De prospectiva pingendi e dunque attraversare le sale è come sfogliarne le pagine. Si inizia dai principi geometrici e si prosegue con le figure piane, i corpi geometrici, l'architettura, la figura umana, la proiezione delle ombre e l'anamorfosi. I disegni del trattato sono trasformati in modelli tridimensionali per illustrare al meglio la logica delle loro costruzioni geometriche, mentre una serie di macchine matematiche progettate dall'Università degli Studi di Modena e Reggio Emilia riproducono scientificamente gli strumenti della bottega dell'artista rinascimentale, permettendo al visitatore di toccare con mano e comprendere gli accorgimenti tecnici adottati dai pittori per sfruttare creativamente gli inganni della visione. Parte integrante del percorso espositivo sono notevoli installazioni multimediali che permettono di comprendere al meglio la celebre Città ideale di Urbino, uno dei capolavori della prospettiva rinascimentale, necessario complemento della trattatistica prospettica. Per informazioni: PIERO DELLA FRANCESCA. Il disegno tra arte e scienza. |

Piero della Francesca, Flagellazione di Cristo, Galleria nazionale delle Marche, Palazzo Ducale, Urbino