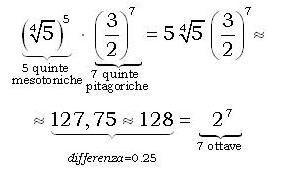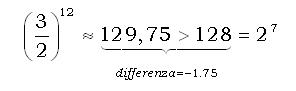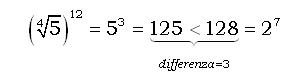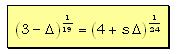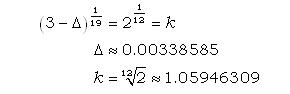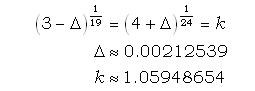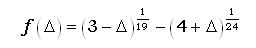Relazioni armoniche in un pianoforte

Il compromesso
Nel 1691 l’organista tedesco Andreas Werckmeister trovò un ingegnoso modo per accordare gli strumenti nel modo più vicino mai realizzato rispetto ad un temperamento equabile [1], ossia ad un sistema tonale in cui il semitono (distanza tra due note successive della scala cromatica) fosse costante. Un’accordatura equabile “esatta” era irrealizzabile in tempi in cui l’Elettronica non esisteva, in quanto il valore esatto di un tale semitono [2] è

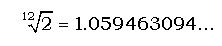
un numero irrazionale algebrico ma “non geometrico”, ossia non riproducibile “con riga e compasso”. Il compromesso acustico di Werckmeister, da lui stesso ribattezzato buon temperamento, si basava sull’uso congiunto di due altri sistemi ben noti e consolidati nei secoli. Con sette quinte pitagoriche (basate sul rapporto 3:2) e cinque quinte mesotoniche (più calanti, costruite a partire dal rapporto di terza 5:4), riusciva a chiudere quasi esattamente il famigerato ciclo delle 12 quinte [2], che arrivavano a corrispondere “quasi” a 7 ottave:
Una tale approssimazione era impossibile da realizzare con sole quinte pitagoriche (o naturali):

o con sole quinte mesotoniche

La scala di Werckmeister ebbe un enorme successo grazie all’uso che ne fece J.S. Bach nel suo Clavicembalo ben temperato (1722 e 1744), per un totale di 24 preludi e altrettante fughe nelle 24 tonalità disponibili (una per ciascuna nota della scala nei modi maggiore e minore). La svolta epocale data alla musica tre secoli fa fu un compromesso geniale tra l’esigenza dei musicisti di accordi “giusti” e naturali e quella dei matematici di intervalli “esatti” e irrazionali.

Frequenze o Battimenti?

Il metodo classico utilizzato dagli accordatori per secoli, diffuso ancora oggi tra chi non si accontenta di usare diavolerie tecnologiche come frequenzimetri e tuner elettronici, si basa sul fenomeno dei battimenti: due note fra loro distanti fino a una ventina di Hertz generano un suono pulsante nel tempo, che può provocare fastidio in chi lo ascolta o che – come avviene ad esempio negli organi – viene appositamente ricercato per ottenere determinati effetti acustici. Ridurre al minimo i battimenti, che venivano fuori dalle approssimazioni “innaturali” delle note, è quindi storicamente sempre stato un obiettivo degli accordatori. Ma finora nessuno si era cimentato a rendere “scientifica” tale ottimizzazione, preferendo percorrere invece la strada più battuta del temperamento delle frequenze.

Dopo una trentennale ricerca e una miriade di tentativi, un maestro accordatore di livello internazionale, il messinese Alfredo Capurso, propone una interessante e rivoluzionaria soluzione al bimillenario problema dell’accordatura, basata su alcune semplici idee. La prima è di non fissarsi sul rapporto di ottava 2:1, ossia sull’uguaglianza pitagorica

ottava = frequenza doppia

in modo da dover incasellare 12 semitoni tra due Do successivi; ma stravolgere le abitudini e ricavare note che suonino “diversamente” a distanza anche di qualche Hz dalla loro frequenza abituale.

In effetti, il sistema temperato risolve matematicamente il problema degli intervalli (rapporti tra frequenze) di una scala tonale, ma con il limite tecnico di dover approssimare tutti gli intervalli tranne l’ottava. Dal punto di vista degli accordatori, ossia della sensibilità armonico-acustica, il problema era quindi stato risolto ingoiando il rospo delle approssimazioni “innaturali” che certo facilitavano il loro lavoro, ma non rendevano giustizia al loro orecchio e al mosaico complessivo di tutte le 88 frequenze principali di un pianoforte.

Nel tempo forse ci si è concentrati troppo sulla matematizzazione della musica fino ad arrivare al “rigido” risultato noto come teorema fondamentale dell’Armonia, ricavato da quello dell’Aritmetica:

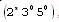
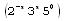
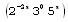
Poiché i tre numeri base sono primi tra loro, sembrerebbe inutile cercare di ignorarne uno dei tre, ossia provare a costruire l’intervallo R senza usare ottave , quinte o terze maggiori . Con il temperamento equabile accade che il rapporto di ottava sia tuttavia l’unico “postulato” alla base del sistema, che trova invece un compromesso proprio per i rapporti di terza maggiore (5:4) e quinta (3:2), universalmente riconosciuti come quelli di maggiore consonanza. Ecco perché, dopo anni di studi, riflessioni e prove tecniche, a Capurso è venuto il lampo di genio: “il fatto che un Do basso sia la metà esatta del Do dell’ottava superiore è soltanto una arbitrarietà matematica; il segreto per scoprire la vera relazione tra una nota e l’altra sta nella sincronia tra i suoni e i loro battimenti”.

E’ un concetto, questo, molto caro ai fisici e portato alla ribalta dagli studi di psicoacustica di H. von Helmoltz, per il quale la consonanza che si avverte tra due suoni è data proprio dal fatto che i battimenti generati da essi e dai rispettivi armonici sono “deboli” rispetto a quanto accade invece in situazioni di dissonanza (come la “quinta del lupo”).

Usando una tecnica di impostazione che potremmo dire opposta alla “musica microtonale”, ossia alla parcellizzazione dell’ottava in più di 12 semitoni, Capurso espande il rapporto di ottava in modo che sia di poco superiore al pitagorico 2:1, che a suo giudizio « non trova né un riscontro logico né uno pratico ».

Come sappiamo [1] una corda tesa che vibrando emette come nota fondamentale un Do di frequenza che poniamo uguale a 1 emette nel contempo un’infinità di altre note secondarie (gli armonici) di frequenza multipla intera (2, 3, 4…) di quella del Do, con intensità via via decrescente in modo che da un certo punto in poi non siano più udibili. Tutti gli infiniti armonici contribuiscono a determinare la “forma” del suono, ossia il suo timbro peculiare.

L’armonico 2 (prima ottava), finora privilegiato, toglie ingiustamente spazio agli armonici 3 (quinta), 4 (seconda ottava) e 5 (terza). Ecco il passaggio successivo del temperamento armonico: mentre la dicotomia tra i rapporti di frequenza 2 e 3:2 non permette di chiudere il ciclo di quinte, dai periodi dei battimenti vien fuori la soluzione. Come spiega Capurso, « si estrae una Radice Armonica che si ripresenta indipendentemente dall’ordine delle grandezze dei suoni generatori ».

Il sistema che ne vien fuori, battezzato Circular Harmonic System (C.Ha.S.^®) dal suo inventore, ha delle peculiarità a dir poco interessanti. La Radice Armonica del Sistema Chas ritrova nel periodo dei battimenti il preciso rapporto tra il 4 e il 3.

Relazioni armoniche

Il temperamento Chas esprime per il suo inventore il più alto grado di armoniosità, da intendersi sicuramente a livello di relazione tra suoni e accordi, tra singole note e l’insieme completo degli 88 tasti del pianoforte. Non più quindi un temperamento basato sul rapporto numerico di due singole note-semitono ma dalla coppia alla molteplicità, al tutto.

Il limite del sistema temperato è, come detto prima, conseguenza di due scelte arbitrarie già entro la prima ottava:

la base numerica di 13 suoni-semitoni;
il rapporto numerico fisso del semitono +13 (frequenza doppia della prima nota).

I valori dei primi 13 suoni trovati vengono abitualmente riportati con un “copia e incolla” verso i bassi e gli acuti, con ulteriori “aggiustamenti” che inevitabilmente scardinano i rapporti tra i suoni fondamentali e le relazioni armoniche dell’insieme completo di 88 note. Per superare questi limiti, prendiamo un intervallo di riferimento più ampio, aprendo il “compasso” a due ottave invece di una.

A Capurso non basta fissare una ragione geometrica k (semitono) per ottenere note successive, ma “un Sistema rivolto a coppie di suoni, così da formare un insieme pluri-direzionale in cui ogni suono-semitono restituisca il significato armonico e la memoria di ogni altro suono, e dove qualsiasi intervallo (coppia di note) risulti pienamente giustificato”. Quindi le giuste proporzioni non vanno ricercate già tra le frequenze entro la prima ottava, ma tra i battimenti espressi da coppie di note con le giuste frequenze: essi possono esprimere una “quiete” (consonanza) o una “tensione” (dissonanza) variabile, determinata dagli armonici silenti.

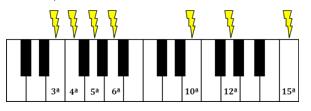
Gli “agenti tensori”, ossia gli intervalli-chiave che assieme all’ottava ritrovata esprimono un preciso andamento di tensione, sono:

la 3ª, la 4ª, la 5ª e la 6ª entro la prima ottava;
la 10ª, la 12ª e la 15ª entro due ottave.

Vanno poi considerate le usuali simmetrie armoniche tra gli intervalli:

3ª maggiore ↷ 6ª minore e viceversa;
6ª ↷ 3ª minore;
4ª ↷ 5ª e viceversa;
4ª eccedente, al centro dell’ottava, in sé stessa.

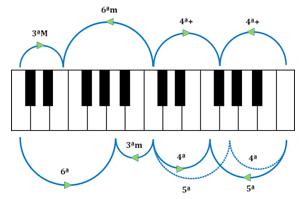
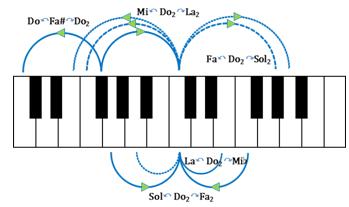
Nella sequenza Do1 (semitono +1), Fa# (+7), Do2 (+13), Fa#2 (+19), Do3 (+25) ogni nota si alterna nella posizione centrale e determina così ben cinque legature armoniche (non solo quella dell’ottava !), che nell’arco +1∩+13 risultano essere:

Do ‑ Fa# ‑ Do2 (4ª+ e 8ª);
Mi ‑ Do2 ‑ La2 (3ª, 8ª e 6ª minore);
Fa ‑ Do2 ‑ Sol2 (4ª, 8ª e 5ª);
Sol ‑ Do2 ‑ Fa2 (5ª, 8ª e 4ª);
La ‑ Do2 ‑ Mib2 (6ª, 8ª e 3ª minore).

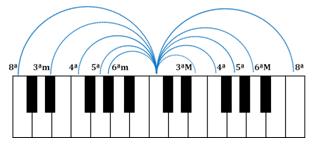
È quindi evidente come, entro due ottave, ciascun semitono abbia 5+5 legature armoniche:

verso destra: 3ª maggiore, 4ª, 5ª, 6ª e 8ª;
verso sinistra: 3ª minore, 4ª, 5ª, 6ª minore e 8ª.

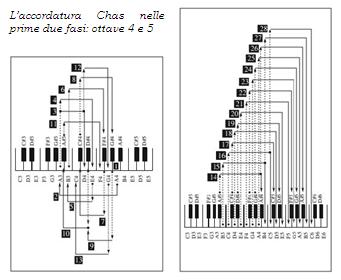
La maggiore armonicità tra più coppie di note, ovvero la consonanza tra più intervalli che quelli classici, fa sì che in questo sistema circolare non resti spazio alcuno per il compromesso. Al contrario, l’approssimazione usuale del semitono scompagina le tensioni armoniche di ben 5 intervalli in un arco di ottava, 10 nell’arco di due e così via. La differenza acustica appare apprezzabilmente diversa a chi, come Capurso, i pianoforti li accorda ad orecchio e non con il tuner. Ad oggi riesce a “sistemare” in 15 minuti la prima ottava (ottava 4 sulla tastiera), in un’ora le prime tre (ottave 3-4-5) e in un paio d’ore tutto lo strumento. Questo viene poi lasciato riposare un po’ per abituarsi alle nuove tensioni-relazioni e permettere eventuali fenomeni di isteresi elastica.

Straordinario è l’effetto che produce ad orecchi allenati l’ascolto di un brano suonato su uno Steinway & Sons temperato Chas (cfr www.chas.it): anche una semplice scala suona in un modo più eufonico, totalmente naturale. Lo capiscono subito i concertisti (ma non solo).

La Radice Armonica

A livello scientifico Capurso è stato seguito da un gruppo di matematici dell’Università di Palermo, guidato dal prof. Filippo Spagnolo. Aveva anche presentato la sua idea nientedimeno che a Benoit Mandelbrot, il papà dei frattali recentemente scomparso, e proprio attraverso lo studio delle forme auto-simili potrebbero un giorno scoprirsi applicazioni meta-musicali di questa creatura e nuove armonie geometriche. In effetti, si ha armonia quando nel tutto ritroviamo il significato di ogni sua singola parte (e viceversa) proprio come accade nel Chas e nei frattali. Per motivi che qui non approfondiamo, si arriva ad un equivalente della sezione aurea in musica, ovvero in 4D, poiché il suono si propaga nelle 3 dimensioni spaziali e nel tempo.

La Radice Armonica, ovvero la “costante armonica di risonanza simmetrica 4:3”, vien fuori dalla seguente formula, che per Capurso è risolutiva del temperamento armonico:

Ecco come l’autore stesso spiega la struttura architettonica del sistema: “il Chas, diversamente dai precedenti sistemi, non riconosce una prevalenza del rapporto 2:1 sugli altri rapporti, e muove invece da un’eguale “valore-differenza”, una medesima distanza di due grandezze (3 e 4), dal loro valore puro. Questa scala proporzionale nel tempo ritrova la ragione matematica in una equi-differenza”. Ogni elemento dell’insieme Chas rinuncia a una piccola parte del suo valore armonico “puro” per ritrovarsi in un “Grande Insieme Armonico”, costituito dai valori 3 e 4 e dai fattori di scala 19 e 24.

Fissato il valore del parametro s e risolvendo l’equazione rispetto a ∆, otteniamo per ambo i membri un fattore costante k. Ad esempio per s=0 si ha il semitono del sistema equabile:

Il sistema Chas si ottiene invece ponendo s=1:

Qui di seguito riportiamo il grafico della funzione

e un suo zoom in un intorno di Δ=0.002

Chas vs Equabile

Entrambi i sistemi, Chas e Temperato equabile, usano quindi rapporti irrazionali tra le note. Ma mentre il sistema temperato equabile è fondato su approssimazioni, ossia su compromessi tra il suono ideale e un suono facilmente calcolabile, il Chas è per Capurso il sistema ideale in cui i numeri irrazionali si usano per eliminare le approssimazioni e creare quindi più armonia.

Le differenze tra le frequenze nei due sistemi appaiono minime ma la loro giustificazione di fondo è, come abbiamo visto, completamente diversa. Analizzando i numeri nel dettaglio scopriamo che, esprimendo i semitoni in cent [3], la differenza si attesta sugli 0.04 cent a nota di modo che, iniziando l’accordatura con il La4 a 440 Hz, il La0 (primo tasto del pianoforte) sarà a soli 0,03 Hz sotto la frequenza usuale 27,50 Hz, mentre il Do8 (ultimo tasto) sarà di 3,61 Hz sopra i 4186,01 Hz abituali.

Tra le due ottave, a fine processo, s’instaura automaticamente lo stesso rapporto che tra i semitoni.

Rimandiamo al sito ufficiale del Chas [6] in cui il metodo è descritto in tutti i dettagli tecnici, scientifici e percettivi. Quello che auguriamo ad Alfredo Capurso è di riuscire a trovare un novello Bach che sposi il suo geniale sistema di accordatura e lo diffonda nel mondo. Impossibile? Non certo nell’epoca della rete globale, grazie alla quale abbiamo conosciuto il Chas, che volentieri rimettiamo al giudizio dei musicisti e dei matematici.

Bibliografia e sitografia

[1] N. Chiriano, “Pitagora e la Musica”, Alice&Bob n. 15, nov-dic 2009

[2] N. Chiriano, “Il restauro della Scala. Il “temperino” di J.S. Bach”, Alice&Bob n. 16, gen-feb 2010

[3] N. Chiriano, “A ritmo di log. G.W. Leibniz e i “numeri dei rapporti” “, Alice&Bob n. 17-18, mar-giu 2010

[4] N. Chiriano, “Onda su onda... J.B. d'Alambert fa luce sul suono”, Alice&Bob n. 19, lug-ago 2010

[5] A. Capurso, “Un nuovo modello interpretativo di alcuni fenomeni acustici: Il sistema formale circolare armonico (circular harmonic system – c.ha.s.)”, Quaderni di Ricerca in Didattica n. 19, 2009 - G.R.I.M. (Dip. Matem., Un. di Palermo)

[6] www.chas.it