In ricordo di Maurice Allais, economista matematico, Premio Nobel nel 1988

All'età di novantanove anni il 10 ottobre scorso a Parigi, nella stessa città dov'era nato, è scomparso Maurice Allais, primo e finora unico premio Nobel assegnato a un economista francese nel 1988. Nella motivazione si legge che il premio Nobel è stato attribuito ad Allais "per i suoi contributi pioneristici alla teoria dei mercati e dell'utilizzo efficiente delle risorse". Una motivazione talmente ampia da suonare vaga, se non generica dietro cui è difficile scorgere il reale contributo di Allais. Una motivazione che lo stesso Allais cercò poi di interpretare, invero senza riuscirvi, come un riconoscimento per aver studiato le condizioni in grado di assicurare che l'economia soddisfi con la massima efficienza i bisogni umani data la limitata disponibilità delle risorse.

Maurice Allais alla premiazione del Nobel per l'economia nel 1988

Il fatto è che Allais, come spesso accade,  non fu economista per vocazione. La fisica e il calcolo delle probabilità erano le sue letture preferite, letture che in seguito avranno un peso rilevante negli sviluppi successivi del suo pensiero. Furono piuttosto le circostanze - una visita nell'estate del 1933 negli Stati Uniti alle prese con la Grande Depressione, i disordini sociali che sconvolsero la Francia all'indomani delle elezioni del 1936 - a spingerlo a dedicarsi a quello che egli riteneva il compito fondamentale dell'economia: "promuovere la maggiore efficienza assicurando al contempo una distribuzione del reddito che sia generalmente ritenuta accettabile". Fu così che poco meno che trentenne e in soli trenta mesi, quando era ancora responsabile del Servizio Miniere e Cave a Nantes e durante gli anni bui dell'occupazione tedesca dal gennaio del 1941 al luglio del 1943, che scrisse un trattato di teoria economica di quasi novecento pagine, "A la Recherche d’une Discipline Economique. L’Economie Pure ". A cui peraltro dovevano seguire, almeno nelle intenzioni, ben altri cinque volumi. I primi tre dedicati all'economia monetaria e all'economia internazionale, il quarto dedicato all'analisi del disequilibrio delle economie reali, mentre l'ultimo doveva avere ambizioni normative, come lascia intuire il titolo, "L’Economie de l’Avenir".

Allais giovane studente nel 1933

Il progetto era talmente ambizioso da apparire irrealistico allo stesso Allais. Esso contiene però gran parte delle idee che verranno in seguito sviluppate e pubblicate. Ne è un esempio il libro del 1947 "Economie et Intérêt", che contiene i materiali elaborati per il terzo e il quinto volume. Di fatto, tutto il lavoro successivo può essere considerato come una progressiva elaborazione del programma pensato all'inizio degli anni quaranta. Ed è sostanzialmente a questo lavoro che la motivazione del Nobel si riferisce.

Ma proprio da questa motivazione è assente l'argomento per cui oggi Allais è noto a gran parte degli economisti. L'oggetto è "Il comportamento dell'uomo razionale di fronte al rischio: Critica ai postulati e agli assiomi della Scuola Americana", come recita (in francese) il titolo del lavoro più famoso di Allais comparso nel 1951 su Econometrica, allora come oggi probabilmente la più  importante rivista di teoria economica esistente al mondo. In realtà, l'argomento svolto nell'articolo è noto oggi come il Paradosso di Allais. Come precisa lo stesso Allais, il paradosso è tale solo in apparenza, ed è così denominato semplicemente perché contraddice il più importante degli assiomi su cui poggia il teorema dell'utilità attesa - ovvero, per usare le parole di Allais, il principio di Bernoulli elaborato dalla Scuola Americana. Tra i principali esponenti della Scuola Americana figuravano Samuelson, Savage e Marschack, oltre che naturalmente von Neumann e Morgenstern che pochi anni prima in "The Theory of Games and Economic Behavior" avevano dato basi assiomatiche all'utilità attesa.

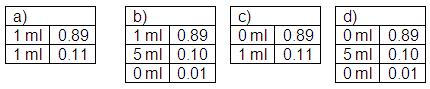
In cosa consiste la critica di Allais? Essa si rivolge sia all'aspetto normativo, ovvero all'utilità attesa come guida all'azione, che all'aspetto descrittivo della teoria, ovvero all'utilità attesa intesa come mezzo per rappresentare il modo in cui vengono prese le decisioni in condizioni di incertezza. Il paradosso riguarda tuttavia soltanto la parte descrittiva. Nel 1952, l'anno precedente la pubblicazione dell'articolo su Econometrica, Allais aveva condotto un centinaio di interviste a soggetti con una buona conoscenza del calcolo delle probabilità e che quindi potevano essere considerati "razionali". Agli intervistati venne chiesto di effettuare una duplice scelta, ciascuna delle quali comportava un'alternativa tra due distribuzioni di probabilità o, come anche vengono denominate, lotterie. La prima scelta riguardava le seguenti due lotterie: a) avere 1 milione di euro con certezza; b) avere 1 milione di euro con l'89 per cento di probabilità e 5 milioni con il 10 per cento. La seconda scelta riguardava due altre lotterie: c) avere 1 milione di euro con l'11 per cento di probabilità; d) avere 5 milioni di euro al 10 per cento. Agli intervistati venne chiesto appunto di scegliere tra a) e b), e poi tra c) e d). Il risultato fu che la maggioranza dei soggetti scelse a) nel primo caso e d) nel secondo. Questo esito è stato poi confermato da numerosi altri esperimenti che proponevano lo stesso tipo di scelta.

La duplice scelta appena illustrata è lo sfondo su cui è costruita la critica di Allais alla teoria dell'utilità attesa e al principio di razionalità che essa sottende. Per comprendere cosa si trovi all'origine di questa critica, si osservi che il secondo problema di scelta non è che una variante del primo a cui è stata sottratta a entrambe le lotterie 1 milione di euro con l'89 per cento di probabilità. Per porre in luce questo aspetto, riformuliamo le quattro lotterie che compaiono nei due problemi di scelta nel seguente modo: a) avere 1 milione di euro con l'89 per cento di probabilità e 1 milione di euro con l'11 per cento di probabilità; b) avere 1 milione di euro con l'89 per cento di probabilità, 5 milioni con il 10 per cento e 0 euro  con l'1 per cento; c) avere 1 milione di euro con l'11 per cento di probabilità e 0 euro con l'89 per cento; d) avere 5 milioni di euro al 10 per cento, 0 euro con l'89 per cento e 0 euro con l'1 per cento (vedi Figura). Questa riformulazione mette in evidenza che c) e d) presentano le stesse possibilità di a) e b), salvo che al posto di 1 milione all'89 per cento, si ha 0 euro sempre con l'89 per cento di probabilità. Insomma, soltanto "apparentemente" siamo di fronte ad un diverso problema di scelta.

Figura. Il doppio problema di scelta proposto da Allais. L'individuo sceglie tra a) e b) e poi tra c) e d).

Ciò dovrebbe implicare che se si sceglie l'opzione a) nel primo problema di scelta, si "deve" poi scegliere l'opzione c) nel secondo, almeno se ci si attiene alla razionalità così come è definita dall'utilità attesa. E viceversa: se si sceglie b) nel primo problema, si "deve" poi scegliere d) nel secondo. Com'è allora possibile che il comportamento osservato contraddica questo principio di razionalità? Una spiegazione può essere la seguente. Nel primo problema si sceglie 1 milione di euro per certo invece che l'altra opzione (1 milione di euro all'89 per cento e 5 milioni al 10 per cento) perché si teme di rimanere senza nulla, anche se questa possibilità ha una probabilità di verificarsi soltanto dell'1 per cento. Nel secondo problema si sceglie di "scommettere" sull'alternativa che offre 5 milioni con il 10 per cento di probabilità piuttosto che quella che dà 1 milione all'11 per cento perché si ritiene che la differenza nell'eventuale vincita più che compensi la riduzione di probabilità.

È proprio questo comportamento che mette in discussione l'assioma principale dell'utilità attesa, l'assioma che Samuelson chiamava di sostituibilità e Savage di indipendenza. L'assioma afferma qualcosa di apparentemente assai evidente. Se si preferisce la lotteria L1 alla L2 (per esempio, l'opzione a) all'opzione b)), allora si "deve" preferire αL1+(1-α)L3 alla lotteria αL2+(1-α)L3, dove L3 è una qualunque altra lotteria e α è un numero compreso tra 0 e 1 (zero escluso). La giustificazione offerta da Samuelson di questo assioma sembra particolarmente cogente. Se si realizza l'evento che ha probabilità α, allora per ipotesi l'individuo ha già detto di preferire L1 alla L2; se invece si realizza l'altro evento che ha probabilità 1-α, l'individuo è evidentemente indifferente tra le due lotterie poiché offrono lo stesso premio. L'assioma viene detto di indipendenza proprio perché la presenza di una terza lotteria L3 come non altera la scelta effettuata in precedenza. D'altra parte, l'assioma è importante perché consente all'utilità attesa di avere la forma di una media ponderata, ossia di presentarsi come una somma delle utilità delle conseguenze presenti in ciascuna scelta (l'utilità attribuita a 5 milioni, a 1 milione, o a 0, nei problemi di scelta proposti da Allais) pesate con le rispettive probabilità. È proprio l'assioma di indipendenza che permette alle utilità delle conseguenze di essere sommate, in cui perciò l'utilità di ciascuna conseguenza è indipendente dalle altre. Ciò che Allais contesta è proprio questa indipendenza. Gli individui, quelli intervistati da Allais e negli altri esperimenti condotti in seguito, sembrano invece manifestare nei comportamenti effettivi una complementarità piuttosto che un'indipendenza nei confronti della terza lotteria, ovvero nelle parole di Allais "il vantaggio psicologico della certezza". È questo vantaggio che spinge i soggetti a scegliere a) nel primo problema e d) nel secondo.

Il paradosso di Allais ha rappresentato un punto di svolta importante per la teoria della scelta in condizioni di incertezza. Non solo perché è stato il primo a porre in luce le violazioni sistematiche al principio dell'utilità attesa attraverso l'evidenza empirica, né per il suo carattere intuitivo. Ma soprattutto perché, malgrado la diffidenza se non l'ostilità resa manifesta dall'aver tradotto in inglese soltanto una breve sintesi dell'articolo (4 pagine su 45) e dalla presa di distanza della nota dell'editore di Econometrica (il cui tono è evidente sin dalla prima frase, "Il problema discusso nell'articolo del professor Allais è assai sottile e sembra difficile raggiungere un consenso generale sulle principali questioni affrontate"), esso ha costituito una svolta decisiva per la teoria economica. Basti qui ricordare che con tutta probabilità (è il caso di dirlo) senza il contributo di Allais non vi sarebbero né la Finanza comportamentale né l'Economia comportamentale, che suscitano oggi tanta attenzione e il cui oggetto di studio è costituito appunto dai comportamenti che non possono essere spiegati sulla base del principio di razionalità della teoria economica, come quelli che molto spesso danno luogo a crisi finanziarie. Ne è ulteriore testimonianza il Nobel per l'Economia assegnato a Daniel Kahneman (condiviso con Vernon Smith), per aver integrato nella teoria economica le intuizioni della ricerca psicologica, soprattutto nello studio del comportamento umano e della scelta in condizioni di incertezza. Una motivazione che sembra essere un riconoscimento implicito al contributo di Allais.