Riposte armonie: dal triangolo rettangolo alla Kampila di Eudosso

Capita, a volte, che alcuni luoghi geometrici interessanti sino ottenuti in modo più semplice rispetto a quelli già noti e che, proprio per questa ragione, abbiano una valenza educativa pregnante, come succede parallelamente in Fisica quando, per illustrare una legge, un esperimento eseguito con mezzi “poveri” può essere didatticamente più efficace di quello condotto con strumenti più sofisticati.

Ciò accade soprattutto quando oggetti matematici noti vengono considerati da un nuovo punto di vista, che consente di interpretarli in maniera più feconda, dando luogo non solo a importanti conseguenze matematiche ma anche a nuove prospettive didattiche.

La situazione è simile a quella di chi osserva il David di Michelangelo, ponendosi soltanto di fronte alla statua, e di chi invece ha la curiosità di osservarla anche dalla parte posteriore, ricavandone una conoscenza più profonda per poterla descrivere più dettagliatamente.

La storia della Matematica ci offre tanti esempi di questo tipo in cui, a volte, una semplice osservazione ha avuto un ruolo decisivo per illuminare di una nuova e inattesa luce argomenti matematici entrati ormai da tempo nella routine. Basti pensare al modo in cui una semplice (ma geniale) osservazione di Niels Abel sull'inversione degli integrali ellittici, studiati in precedenza per più di quarant'anni da Adrien Marie Legendre, inaugurò lo studio vasto e profondo delle funzioni trascendenti note come funzioni ellittiche.

Con lo stesso spirito, vogliamo illustrare come alcune considerazioni elementari sul caro e vetusto triangolo rettangolo possano offrire spunti interessanti non solo per ricavare in maniera nuova risultati già noti, ma anche per darne una trasposizione didattica non priva di interesse nell'insegnamento della Matematica (sia liceale che universitario). Infatti alcuni calcoli, altrimenti tediosi, sono stati eseguiti mediante il software Mathematica® guidato opportunamente dal solutore, il che costituisce un esempio dell'uso consapevole di un software. Può essere un interessante esempio di interplay (per usare un termine inglese) tra la scoperta matematica, ?ltrata attraverso la storia della Matematica, e la sua trasposizione didattica coadiuvata dal computer.

 Consideriamo dunque il triangolo rettangolo AOB della figura 1 e riferiamolo a un sistema di assi cartesiani ortogonali con A (a, 0) e B (0, b). Sia r la retta per A e B di equazione bx+ay-ab=0.

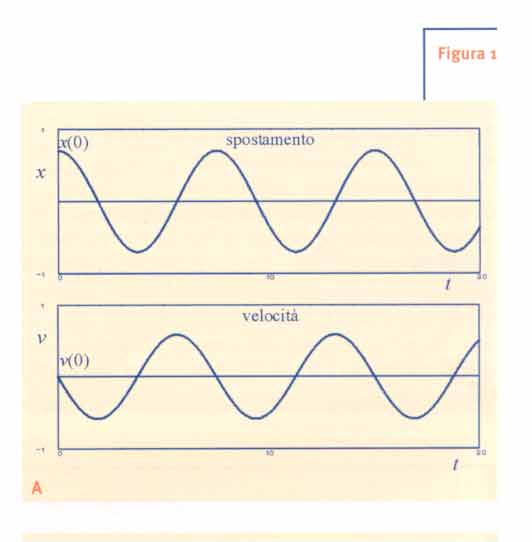
Figura1

Sia y = mx una qualunque retta t per O≡(0, 0) e sia T il punto di intersezione tra essa e AB. Le coordinate di T saranno:

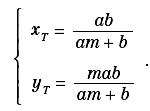
Riportiamo il segmento OT su OA. A tale scopo, determiniamo l’intersezione tra la circonferenza di centro O e raggio uguale alla lunghezza del segmento OT con l’asse x. Il punto K di intersezione avrà ascissa:

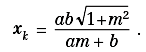
Allora, il punto P d’intersezione tra la retta per K perpendicolare ad OA e la retta t avrà coordinate:

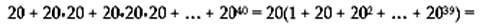
Eliminando il parametro m in (1), si ottiene il luogo del punto P (al variare di t) di equazione:

b²x⁴ + 2abx³y + a²x²y² - a²b²x² - a²b²y² = 0. (2)

La curva è simmetrica rispetto all’origine, che è un punto doppio isolato da cui escono le rette isotrope:

y = ±i x.

La curva possiede, inoltre, due asintoti verticali di equazione:

x = ±b.

Per la ricerca degli asintoti obliqui, com’è noto, annullando i termini di grado massimo dell’equazione della curva, si ha:

b²x⁴ + 2abx³y + a²x²y² = 0 (3)

dalla quale, dividendo per x⁴ e ponendo y/x = m, si ottiene m = -b/a contato due volte, per cui l’equazione dell’asintoto sarà del tipo y = -b/a x + p.

Mettendo a sistema questa retta e la curva, si ottiene l’equazione risolvente in x di grado minore di 4. Da questa, annullando il coefficiente della massima potenza di x, si ottiene un’equazione in p che ha come soluzione p=0 per cui la curva ammette l’asintoto obliquo:

y = -b/a x

che risulta parallelo alla retta per A e B. La curva è mostrata in figura 2.

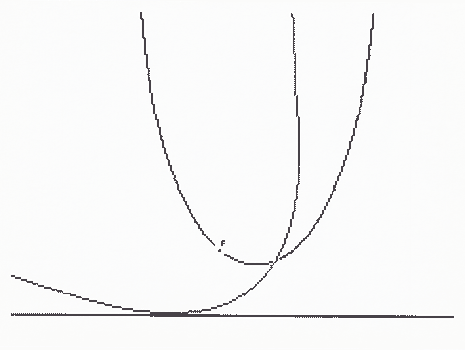
figura 2

Se nella (3) dividiamo per a² e facciamo tendere a all’infinito, ovvero consideriamo il triangolo rettangolo degenere, otteniamo la curva di equazione:

x²y² – b²x² – b²y²=0, (4)

che è l’equazione di una celebre quartica (Bibl. [A] e [B]) chiamata per la sua forma curva a croce (figura 3).

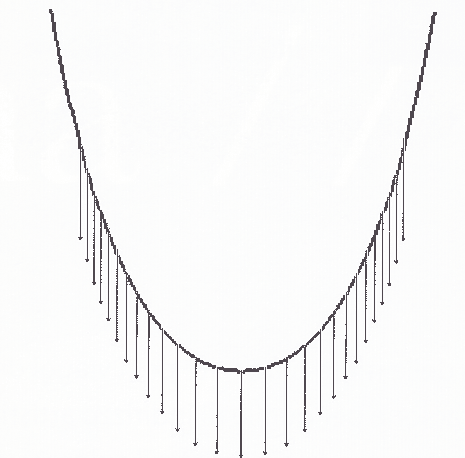
figura 3

In generale, la curva a croce ha equazione:

x²y² – a²x² – b²y² = 0,

la quale, per a = b, viene detta equilatera o circolare retta e assume la forma della (4). Quest’ultima può anche essere rappresentata dalle equazioni parametriche:

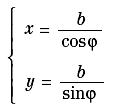
dove φ è un parametro che rappresenta l’angolo formato dalla semiretta variabile OP con l’asse x. L’origine è un punto doppio isolato e i punti all’infinito degli assi sono nodi d’inflessione. I punti reali della curva sono esterni alle strisce limitate dalle equazioni x=±a e y=±b.

Questa curva si incontra sin dal 1847 in una questione proposta dal matematico francese Olry Terquem [1] (1782-1862) e, tredici anni dopo, in un lavoro giovanile (Bibl. [C]) del matematico italiano Angelo Francesco Siacci [2] (1832-1907), il quale dimostrò una bella proprietà della quartica: la somma delle aree limitate dai quattro rami della curva e dai rispettivi asintoti è uguale all’area del rettangolo formato dagli asintoti stessi.

Angelo Francesco Siacci

La curva fu studiata anche da Ernesto Cesàro (1859-1906) che la chiamò stauroide, dal greco σταυροειδης, che significa a forma di croce, proprio per la sua forma.

La curva a croce circolare retta gode inoltre della proprietà che le podarie [3] del centro rispetto ad essa e alla sua evoluta hanno la stessa area.

Ernesto Cesàro

La curva a croce, che si è ottenuta come caso particolare della (3), può essere generata anche nel seguente modo. Si consideri un’ellisse (figura 4) di equazione:

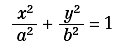
e si tracci la retta tangente in un suo punto qualsiasi M. Detti A e B i punti di intersezione della tangente con gli assi, si conducano per essi le rette m, n parallele agli assi e sia P il loro punto di intersezione. Esso sarà un punto della curva a croce.

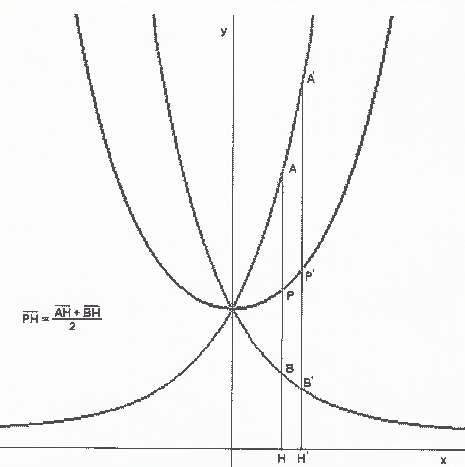
figura 4

Se, al contrario, dividiamo la (3) per b² e facciamo tendere b all’infinito, otterremo la quartica di equazione:

x⁴ - a²x² - a²y² = 0, (5)

il cui grafico è illustrato nella figura 5.

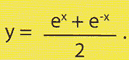
Figura 5

Essa interseca l’asse delle x in (-a, 0) e (a, 0) ed è la famosa (Bibl. [A], [B]) curva Kampila (χαμπυλη γραμμη) che, secondo lo storico francese Paul Tannery, fu utilizzata dal grande matematico greco Eudosso di Cnido (c. 408 - c. 355 a.C.) per eseguire sul piano la costruzione architettata dal suo maestro Archita di Taranto (c. 400 - c. 360 a.C.) per risolvere il celebre problema della duplicazione del cubo (detto anche problema di Delo) in cui si chiedeva di costruire con riga e compasso un cubo di volume doppio di quello di un cubo dato.

Archita di Taranto

Poichè Ippocrate di Chio (V sec. a.C.) aveva mostrato che, per determinare il lato del cubo da costruire,

bastava inserire due medie proporzionali tra il lato del cubo noto e quello incognito, Archita – per riuscire in ciò – escogitò una soluzione ingegnosa che ancora oggi non può suscitare che ammirazione. Infatti, riuscì a risolvere il problema di Ippocrate determinando l’intersezione tra un cilindro, un toro e un cono, rappresentati dalle tre seguenti equazioni (dove è a > b):

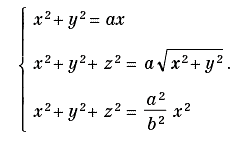
La kampila può anche essere ottenuta come caso particolare di curve deducibili da una conica. Sia, infatti, M un punto qualsiasi dell’ellisse:

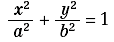
e sia T il punto di intersezione della tangente all’ellisse in M con l’asse x (figura 6).

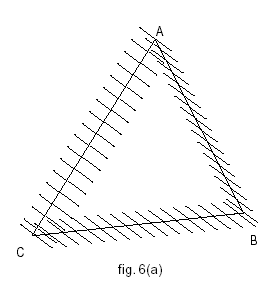
figura 6

Sia M′ l’intersezione tra la retta OM con la parallela all’asse y condotta da T. Il luogo del punto M′(x′, y′) si otterrà eliminando x e y tra le tre equazioni:

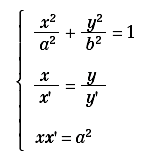
La sua equazione sarà:

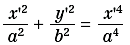
la quale, per a = b, si riduce all’equazione della Kampila.

Se invece, sempre con riferimento alla figura 6, si considera l’intersezione H tra la normale in M all’ellisse e la parallela per T all’asse y, l’equazione del luogo del punto H(x1, y1) si otterrà eliminando x e y tra le tre equazioni:

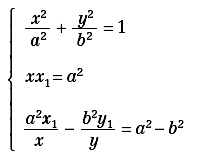
ottenendo:

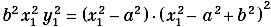
da cui, per a = b, si ha nuovamente l’equazione della Kampila.

La curva a croce e la Kampila si riducono alle due rette isotrope uscenti dall’origine sia quando nella (3) dividiamo per b² e facciamo tendere b a infinito, sia quando nella (4) dividiamo per a² e facciamo tendere a all’infinito.

Il modo con cui si è ricavata l’equazione della curva a croce si presta ad un uso didattico ragionato della Computer algebra. Infatti, i calcoli tediosi necessari per eliminare il coefficiente angolare m nel sistema irrazionale (1) sono rapidamente svolti mediante Mathematica® ma il software va guidato opportunamente. Il docente dunque, anche al livello della scuola superiore, può utilizzare l’esempio in oggetto per introdurre all’uso consapevole del software, senza perdere di vista gli effetti scenici dati dalla rappresentazione delle curve piane in Mathematica®.

Dall’istruzione per risolvere (1), unitamente alla risposta del sistema illustrata in figura 7, vediamo che in questo modo Mathematica® non solo elimina il coefficiente angolare m ma fornisce anche l’equazione esplicita del luogo, che è:

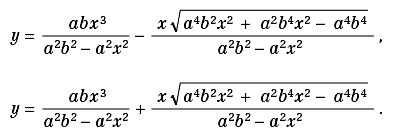
Figura 7

Successivamente, il software può essere impiegato per scrivere l’equazione implicita della curva a croce mediante le istruzioni esplicitate nella figura 8:

figura8

Infine, caricando il package ImplicitPlot, si ottiene agevolmente la rappresentazione grafica della curva a croce attraverso il software, fissando naturalmente prima i valori di a, b e c.

Abbiamo così potuto mostrare come, partendo da una figura familiare come il triangolo rettangolo, con semplici considerazioni geometriche, due celebri curve che storicamente si erano ottenute in modi diversi, appaiono ora legate entrambe dalla particolarizzazionedi un’unica curva rappresentata dall’equazione (2).

Questo offre una visione unitaria delle curve e, come già abbiamo detto all’inizio, mostra come, spesso, in Matematica basta cambiare punto di vista perchè improvvisamente argomenti apparentemente scollegati trovino una loro collocazione comune. Tutto ciò – come ogni altro caso che offra una visione unitaria della Matematica – ha una valenza educativa rilevante.