Saramago matematico non euclideo
José Saramago, scrittore portoghese, autore di romanzi di culto come “Cecità”, vincitore del premio Nobel per la Letteratura nel 1998, è a mio parere un autore dallo stile profondamente matematico pur non avendo mai parlato esplicitamente di Matematica nei suoi libri. Ritengo infatti che i romanzi di Saramago esprimano in letteratura lo stesso spirito delle geometrie non euclidee (e della Matematica moderna in generale). Per giustificare questa affermazione occorre ripercorrere, brevemente, la storia della “rivoluzione non euclidea” nella Matematica di fine Ottocento.
Ricordiamo anzitutto che una teoria matematica, in quanto tale, è formulata secondo canoni ipotetico-deduttivi. Questo significa partire da poche affermazioni di base (dette assiomi) e dedurre, cioè dimostrare mediante determinate regole logiche di ragionamento tante altre affermazioni, dette teoremi. In sostanza, una teoria matematica afferma che “se siamo disposti ad accettare come veri gli assiomi, allora sono veri anche tutti i teoremi dedotti a partire da questi”.
Nella geometria euclidea, cosi come nella maggior parte delle teorie con struttura matematica (come la Fisica ad esempio), gli assiomi sono considerati verità evidenti (self-evident truth) o basati su osservazioni empiriche largamente condivise come certi esperimenti cruciali della Fisica su cui poggiano intere teorie.
I teoremi, ovvero le affermazioni dedotte dagli assiomi nella forma del se… allora…, sono in genere meno evidenti ma, essendo dedotti dagli assiomi mediante ineccepibili argomentazioni logiche (ovvero dimostrazioni), ne conservano lo stesso valore di verità.
Esempio insuperato di questo modo di operare (che è l’essenza del metodo matematico) è la Geometria di Euclide che tutti abbiamo studiato a scuola (in forma più o meno rigorosa) sulla base dell’esposizione data dal grande matematico greco circa 23 secoli fa nei suoi Elementi. Tutto l’edificio formato dai teoremi della geometria di Euclide si basa su cinque assiomi che possono essere espressi come segue:
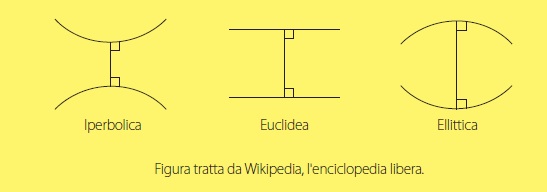
1) tra due punti qualsiasi è possibile tracciare uno ed un solo segmento; 2) si può prolungare un segmento oltre i due punti indefinitamente; 3) dato un punto e una lunghezza, è possibile descrivere un cerchio; 4) tutti gli angoli retti sono uguali; 5) se una retta che taglia due rette determina dallo stesso lato angoli interni minori di due angoli retti, prolungando le due rette, esse si incontreranno dalla parte dove i due angoli sono minori di due retti.
Quest’ultimo assioma può essere riformulato nella forma più moderna: “per un punto passa una ed una sola parallela ad una retta data”.
Ci si può chiedere cosa accadrebbe a una data teoria matematica se si modificasse (o cancellasse) uno degli assiomi su cui si basa. Ad esempio, dalla geometria euclidea si possono ottenere altre geometrie (dette non euclidee) modificando o non accettando alcuni dei suoi postulati. E quanto fece Gerolamo Saccheri (1667-1733), docente di Matematica presso l'Università di Pavia, che nel trattato “Euclides ab omni naevo vindicatus” cercò di dimostrare il postulato delle parallele usando i primi quattro assiomi. Non riuscì nell’intento ma nel tentativo effettuato giunse a dimostrare tutta una serie di teoremi che, pur essendo in contrasto con l'intuizione nello spazio ordinario, costituivano una teoria logicamente coerente e non contraddittoria (sebbene in apparenza assurda). Poi nel corso del XIX secolo si svilupparono altre possibili geometrie, dalla negazione del quinto postulato o del secondo, grazie alle opere di matematici come Gauss, Lobacewski, Bolyai e Riemann.
Fu una vera e propria rivoluzione in Matematica che portò ad accettare il fatto che gli assiomi ce li possiamo inventare, indipendentemente dal fatto che esprimano proprietà evidenti dello spazio fisico o dell’intuizione, purché non siano contraddittori.
Insomma, venne introdotta la distinzione tra "verità" e "coerenza" e una teoria matematica fu spogliata di ogni pretesa attribuzione di verità, essendo i suoi assiomi di base pure convenzioni sulle quali il matematico costruisce l’edificio ipotetico-deduttivo.
Quindi non potremo dire se i teoremi dedotti sono veri nel senso tradizionale di asserzioni avvalorate dall’esperienza sensoriale, ma soltanto affermare che sono deducibili da un insieme di assiomi coerenti, non contraddittori.
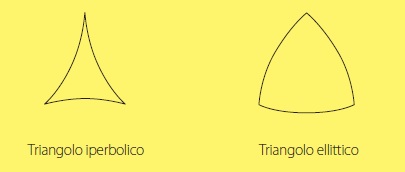
Geometrie non euclidee Una geometria non euclidea è costruita negando o non accettando alcuni postulati euclidei (elencati nell’articolo). In particolare, per quanto riguarda l'enunciato del quinto postulato, che come si è detto può essere enunciato come segue: Data una retta ed un punto non appartenente ad essa, esiste ed è unica la retta passante per il punto e parallela alla retta data, ci si accorge subito che la sua negazione è legata ai concetti di unicità e di esistenza della retta parallela. Quindi le possibili negazioni del quinto postulato sono due, una che nega l'unicità della parallela e l'altra che nega la sua esistenza e possono essere così formulate: 5.1 Data una retta ed un punto non appartenente ad essa, esistono infinite rette passanti per il punto e parallele alla retta data. 5.2 Data una retta ed un punto non appartenente ad essa, non esiste alcuna retta passante per il punto e parallela alla retta data. A seconda di quale delle due negazioni si adotti, si ottiene una diversa formulazione della geometria, detta rispettivamente iperbolica e ellittica. La geometria iperbolica fu studiata dapprima da Carl Friedrich Gauss (1777-1855) e poi da Janos Bolyai (1812-1860) e Nikolai Lobachevsky (1793-1856) e fu la prima geometria non euclidea ad essere sviluppata e divulgata. Fu chiamata iperbolica da Felix Klein (1849-1925) nel 1871. In greco “iperbole” significa “eccesso” e in effetti in tale geometria il numero delle rette parallele ad una retta data e passanti per un punto fissato è in eccesso rispetto a quello (una e una sola) della geometria euclidea. L’altra geometria, ancora da Klein denominata ellittica, fu introdotta da Riemann (1826-1866) e nega l'esistenza di rette parallele. Ciascuna delle due geometrie non euclidee si sviluppa autonomamente, con tutte le conseguenze (ovvero teoremi) che ne caratterizzano le proprietà. Ad esempio, mentre nella geometria euclidea in ogni triangolo la somma degli angoli interni è uguale a un angolo piatto, cioè 180°, nella geometria iperbolica in un triangolo la somma degli angoli interni è minore di 180° e in quella ellittica la somma degli angoli interni è maggiore di 180°.
|
Detto ciò, possiamo tornare a Saramago che nei suoi libri cerca di verificare, con lucide deduzioni logiche, cosa accadrebbe se modificassimo qualche assioma (o convenzione) su cui si basa la nostra società e la nostra vita. Ad esempio, cosa accadrebbe se nel territorio di una nazione non morisse più nessuno, come si legge nel romanzo “Le intermittenze della morte”? Così Saramago prova a dedurre, con rigorosa coerenza e sequenzialità, quali sarebbero le conseguenze di quella strana ipotesi nel contesto sociale, economico, politico e psicologico.
Ma non si ferma qui e arriva a chiedersi cosa potrebbe accadere se esistessero individui perfettamente identici in ogni dettaglio, in modo da renderli del tutto indistinguibili, come narra nel romanzo “L’uomo duplicato”, in cui si nega l’assioma di “individualità” o “specificità” di ogni essere umano. Si tratta della negazione di un principio in apparenza non essenziale, di un piccolo episodio che accade solo per una coppia di individui. Ma le conseguenze di questo dettaglio, esaminate con cura e valutate da Saramago fino alle estreme deduzioni logiche, arrivano a risultati inimmaginabili a priori, proprio come nelle Geometrie non euclidee sono state dedotte conseguenze lontane dal senso comune che però in ultima analisi derivano soltanto dalla modifica del postulato delle parallele.
Molte opere di Saramago iniziano con un avvenimento inaspettato, surreale o impossibile. Non ci si deve domandare come sia potuto accadere: è successo, punto e basta. Poi tutti gli avvenimenti successivi accadono secondo i normali canoni e convenzioni. Però da quel singolo insolito avvenimento iniziale scaturiscono tante conseguenze, attraverso catene di deduzioni e normali passaggi logici, coerenti e realistici. Questo è ciò che Saramago ci racconta, ad esempio, nel romanzo “Cecità”, dove nelle prime pagine l’autore ipotizza che tutti gli abitanti di una nazione diventino ciechi (tutti tranne uno, per essere precisi) e analizza quello che ne potrebbe conseguire. Oppure, se in una nazione quasi tutti gli elettori votassero scheda bianca in una data tornata elettorale, come accade nel primo capitolo di “Saggio sulla lucidità”, come reagirebbe la classe politica e quali posizioni prenderebbero i giornali? E che dire poi se un giorno, all’improvviso, l’intera penisola iberica si staccasse dall’Europa e cominciasse a vagare nell’Oceano Atlantico dirigendosi verso il continente americano, come accade nel romanzo “La zattera di pietra”? Cosa farebbero gli abitanti e quali misure metterebbero in atto i governi spagnolo e portoghese? Si tratta evidentemente di situazioni assurde, espresse talvolta anche con tono ironico e sarcastico, che permettono all’autore di dare giudizi severi sulle possibili incongruenze e debolezze della società, della politica, della Chiesa e anche degli uomini contemporanei che, nonostante la loro esperienza e presunzione, si trovano spiazzati di fronte a eventi inattesi e di colpo mostrano tutta la loro fragilità.
Emblematico è il romanzo “Storia dell’assedio di Lisbona” in cui un revisore di bozze si trova a correggere il testo di un libro in cui si narra l’assedio di Lisbona del 1147 grazie al quale, con l’aiuto dei crociati, i portoghesi riconquistarono la città dominata dai mori. Ebbene, cedendo a un’inspiegabile tentazione, il revisore aggiunge un "non" al testo originale: i Crociati "non" aiutarono i portoghesi.
Questo banale episodio cambiò la vita del revisore il quale, convocato in casa editrice per le doverose spiegazioni, vi trova una nuova funzionaria che rimane affascinata dal suo gesto e anziché licenziarlo se ne innamora e lo incoraggia a scrivere una “sua storia” dell'assedio tenendo fede al "non" aggiunto. Saramago specifica che ciò porterà a una storia falsa, ma coerente e quindi perfettamente verosimile in tutto quello che ne segue, una vera e propria alternativa alla storia vera e che viene a trovarsi, dal punto di vista logico, sullo stesso piano.
Proprio come nel caso delle geometrie non euclidee, in questi romanzi si chiede al lettore di sospendere per un attimo il comune senso di realtà, inserendo un aspetto nuovo, inaspettato e persino impossibile, assurdo, e semplicemente di credervi. Accettato questo, ogni conseguenza sarà dedotta con rigore, quindi perfettamente coerente e persino ovvia. Questo è proprio ciò che si richiede non solo nell’approccio alle geometrie non euclidee, ma anche nella Fisica quantistica o nella relatività. Ad esempio, nella relatività ristretta Einstein ci chiede di accettare come assioma il principio secondo il quale la velocità della luce e una costante universale, cioè ammettere che sebbene sia vero che quando due treni si incrociano viaggiando ciascuno a 100 Km all’ora ciascun viaggiatore vede quelli dell’altro treno muoversi ai 200 all’ora rispetto a se stesso, ciò non accada invece quando i due treni dovessero viaggiare a 300 mila Km al secondo, la velocità della luce. Ciascun viaggiatore vedrebbe quelli dell’altro treno muoversi ancora alla stessa velocità, 300 mila Km al secondo, relativamente a se stesso. Un’affermazione impossibile per il senso comune ma Einstein, partendo da questo assioma apparentemente assurdo, arriva a dedurre conseguenze altrettanto assurde (in apparenza) ma che si sono rivelate poi vere come i teoremi affermano la contrazione delle lunghezze, la dilatazione dei tempi (fino al famoso paradosso dei gemelli) e persino l’equivalenza fra massa ed energia. Affermazioni in apparenza paradossali ma deducibili dall’evidenza sperimentale che la velocità della luce è costante e dal vecchio principio di relatività galileiano, quello sperimentato nella stiva della nave in moto rettilineo uniforme. Se siamo disposti ad accettare quei due assiomi, allora dobbiamo per forza accettare anche tutto il resto.
Analogamente, chi è disposto a credere nel principio di indeterminazione e nell’ipotesi che l’energia si trasmette in pacchetti discreti e non in quantità qualsiasi, potrà poi apprezzare le stupende (e utili) deduzioni della Fisica quantistica, dai fenomeni di diffrazione delle particelle (e quindi il dualismo fra onde e corpuscoli) fino all’effetto fotoelettrico e l’effetto tunnel.
Possiamo quindi dire che leggere Saramago ci abitua alla logica assiomatico-deduttiva e che le sue opere possano essere inserite a pieno titolo in quel filone letterario che Calvino ha definito “letteratura deduttiva”, un tipo di letteratura che, analogamente a quanto avviene nelle discipline scientifiche, parte da pochi elementi iniziali e li sviluppa coerentemente attraverso le dimostrazioni di lemmi, teoremi e corollari.