Spunti sulla divulgazione matematica

1 L’articolo di Roberto Natalini “MADDMATHS! tre mesi dopo - http://maddmath.simai.eu” [v. Matematica - News - Altri eventi] (pubblicato anche nel sito http://maddmath.simai.eu) mi ha stimolato a proporre alcuni spunti sulla divulgazione matematica (come particolare divulgazione non soltanto in ambito scientifico), anche in relazione a possibilità offerte da internet.

2.1 Il primo spunto è quello della riflessione sulla locuzione divulgazione matematica, che può essere intesa in vari modi ed essere più o meno gradita in relazione a valutazioni personali (v. accezione estensiva di § 2.2).

Per comodità del lettore riporto indicazioni del vocabolario on line del Portale Treccani:

divulgazióne s. f. [dal lat. tardo divulgatio -onis]. – L’azione, il fatto di divulgare, d’essere divulgato: d. di notizie false o tendenziose, reato punito dalla legge; d. di segreti d’ufficio, di notizie o informazioni riservate. In partic., diffusione di teorie o dottrine scientifiche, filosofiche, politiche, economiche, ecc., attraverso esposizioni piane e compendiose, senza tecnicismi, e insieme sufficientemente sistematiche, sia come fine a sé stessa, sia con lo scopo di interessare un sempre più largo strato sociale alle nuove scoperte, al progresso del pensiero e della scienza e di contribuire all’elevazione politico-culturale delle masse: fare opera di d.; libri di d. scientifica (talora con leggero senso spreg.: è un’opera di d., volendo significare che ha scarsa originalità e scarso valore scientifico).

È facile rendersi conto che ci sono tipi e livelli diversi di divulgazione matematica e che un ruolo molto importante è svolto dalla scuola.

2.2 Ritengo opportuno invitare a riflettere su quali lemmi si considerano sinonimi di divulgazione o, comunque, collegabili a divulgazione dai vari punti di vista, corrispondenti agli interessi personali.

Il volume Sinonimi e contrari de Il vocabolario Treccani (Roma, 2003) riporta:

• per l’accezione “il rendere noto o l’essere reso noto a tutti” i sinonimi comunicazione, diffusione, propagazione; il sinonimo analogo propaganda; l’opposto occultamento;
• per l’accezione estensiva “esposizione semplificata di concetti complessi, specialmente scientifici: divulgazione scientifica” i sinonimi diffusione, semplificazione, spiegazione, volgarizzazione.

Si noti che (come già accennato in § 2.1) proprio l’accezione estensiva può essere causa (ragionevole) di non gradimento del termine.

Accanto ai verbi che si ricavano da queste indicazioni, e cioè (in ordine alfabetico):

• comunicare, diffondere, divulgare, propagandare, propagare, rendere noto, semplificare, spiegare, volgarizzare,

invito a considerare i seguenti (pure in ordine alfabetico) per un elenco personale:

• collocare in quadro di riferimento, dare un quadro di riferimento, documentare, educare, esortare alla conoscenza, esporre, far capire, far conoscere, guidare alla conoscenza, guidare alla consapevolezza culturale, indirizzare, informare, insegnare, invitare alla conoscenza, orientare in gestione dell’accumulo di sapere, presentare, promuovere, pubblicizzare, segnalare, sensibilizzare, stimolare.

3.1 Prima di proporre altri spunti, mi pare opportuno invitare a considerare la divulgazione matematica secondo la teoria della comunicazione (nel senso di commune facere, cioè fare, rendere comune).

Come è ben noto, sulla comunicazione ci sono studi di più scuole di pensiero, che utilizzano linguaggi settoriali almeno in parte differenti.
Da più di trent’anni utilizzo la terminologia degli studi di Padre Nazareno Taddei sj [2], sia per occasioni di collaborazione, sia per la mia adesione alla impostazione da lui sviluppata [3].

3.2 Un aspetto che ritengo particolarmente utile della teoria della comunicazione è quello della utilizzazione di schemi, che hanno un significativo riferimento non soltanto storico in quello riprodotto in figura 1 ed elaborato da Claude Elwood Shannon, ma spesso chiamato di Shannon e Weaver (con riferimento al libro citato sotto) [4].

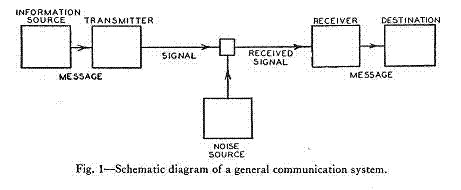
Figura 1

La figura 1 è ripresa da p. 5 di The Mathematical Theory of Communication di C. E. Shannon e W.Weaver (Urbana, The University of Illinois Preess, 1949) [5], che contiene, con un saggio di Warren Weaver [6], l’articolo “A mathematical Theory of Communication” di C. E. Shannon (The Bell System Technical Journal, 1948, luglio e ottobre, pp. 379-423, 623-656; lo schema è a p. 381).

Del libro esiste l’edizione italiana La teoria matematica delle comunicazioni (Milano, Etas Libri, 1971 e 1983), con lo schema riprodotto in figura 2 (da p. 36).

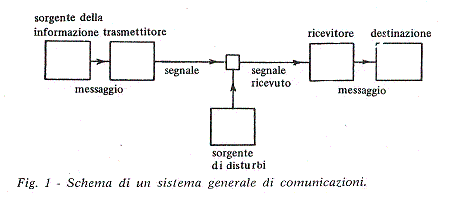
Figura 2

 3.3 Dell’impostazione di N. Taddei mi pare opportuno riprendere (dal libro citato in nota 2, p. 87) lo schema di figura 3, che è l’ultima del capitolo sulla comunicazione e che evidenzia [7]:

• recettore (R) e comunicante (S);
• segno (s) e cosa conosciuta dal comunicante (r):
• rapporto indiretto del recettore con r (con il tratteggio).

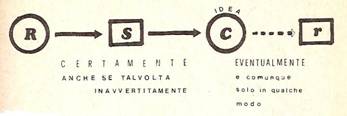
Figura 3

3.4 Collegando gli schemi di figura 2 e di figura 3 ho proposto quelli di figura 4 (lezioni dell’a.a. 1976-1977 [8]), qui riscritta [9], e di figura 5 (1979 [10], v. nota 3).

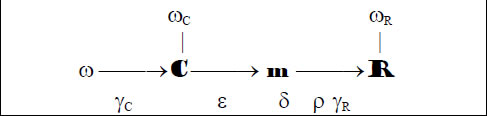
Figura 4

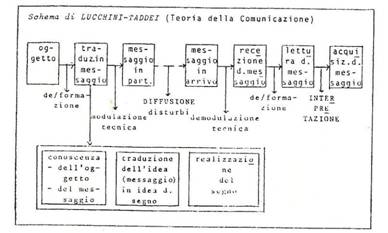
Figura 5

Si noti che il processo può essere evidenziato con le frecce in relazione al recettore, come in figura 3, o in relazione al comunicante, come in figura 4 e in figura 5 (v. nota 9).

I codici di figura 4 indicano [11]:

• C: comunicante
• R: recettore
• m: messaggio (o testo della comunicazione)
• omega: oggetto del messaggio
• omegaC: idea del comunicante sull’oggetto del messaggio
• omegaR: idea del recettore sull’oggetto del messaggio
• gammaC: conoscenza dell’oggetto del messaggio da parte del comunicante
• epsilon: espressione
• delta: diffusione
• ro: recezione o lettura
• gammaR: conoscenza dell’oggetto del messaggio da parte del recettore

3.5 Gli schemi delle figure 3 e 4 sono riferiti alla situazione di un comunicante e un recettore, ma possono essere adattati senza difficoltà a situazioni di:

• più comunicanti, eventualmente coordinati o interagenti tra loro;
• più recettori, eventualmente collegati o interagenti fra loro, in particolare nella scuola;
• interazione del recettore (o recettori) con il comunicante (o comunicanti), con risposte o con dialogo, in particolare nella scuola, eventualmente con opportune soluzioni tecniche (v. § 4.7), anche di percorsi dipendenti dalle risposte.

4.1 Per riflessioni personali sugli elementi della comunicazione segnalati in figura 4, invito i a tenere presente, per quanto possibile, lo schema delle 5w+1 [12] (ordinate alfabeticamente sulla versione italiana):

• what, who, where. why, when + how;
• che cosa, chi, dove, perché, quando + come;

4.2 Come spunti sul comunicante (C) propongo [13]:

• tipo:
  
  • enti istituzionali, enti pubblici, privati; associazioni, gruppi, singoli;
  • organizzatori, autori;
  • matematici ricercatori, insegnanti, cultori, divulgatori con preparazione specifica, divulgatori senza preparazione specifica;
• livello di competenza, qualificazione, autorevolezza sia generiche e sia specifiche;
• obiettivi:
  • informazione, proposta culturale, propaganda, promozione;
  • segnalazione, presentazione, trattazione di argomento;
  • collocazione in un quadro di riferimento, guida culturale a gestione dell’accumulo di proposte, collegamenti interdisciplinari, riflessioni critiche (anche non matematiche);
  • contributo a far conoscere Matematica o suoi settori [14] o aspetti, risultati, teorie, temi, riflessioni, persone o loro lavori, varie mentalità di matematici [15];
• motivazione:
  • segnalazione di propri lavori (autodivulgazione), in particolare nuovi;
  • segnalazione di lavori di altri (mediazione), in particolare di “scuola di pensiero” alla quale si aderisce;
  • promozione della Matematica; contributo a progetto;
  • esposizione di proprio punto di vista;
• impegno:
  • sull’argomento matematico;
  • sulla metodologia comunicativa;
  • occasionale, sistematico;
  • personale o in progetto;
• scelte:
  • oggetto, destinatari, medium [16], impostazione, livello, strumenti, tipo di comunicazione;
  • idea di Matematica (del dimostrare, del capire, del fare, del comunicare);
  • riferimenti sull’argomento, riferimenti metodologici.

Aggiungo tre citazioni, che ritengo significative sull’argomento (potete leggerle cliccando su "Apri approfondimento"):

Ennio De Giorni

Godfrey Harold Hardy

Federigo Enriques

4.3 Come spunti sul recettore (R) propongo:

• tipo:
  • matematici, insegnanti, utilizzatori di Matematica, cultori, studenti, …;
• livelli di preparazione sia generale e sia specifica;
• obiettivi;
• motivazione:
  • interesse a conoscere;
  • necessità di conoscenze (operative, formative, culturali);
  • occasione;
• difficoltà tecniche della Matematica;
• impegno
• difficoltà psicologiche.

4.4 Come spunti sull’oggetto del messaggio (omega) propongo (dal punto di vista del comunicante):

• importanza dell’oggetto; novità; attualità;
• argomenti:
  • matematici, sia generali e sia particolari;
  • storici e fondazionali;
  • sociologici, psicologici, pedagogici e didattici;
  • persone, opere;
• interesse per l’argomento: v. obiettivi di § 4.2;
• difficoltà per il comunicante;
• difficoltà per il recettore.

4.5 Come spunti su conoscenza dell’oggetto del messaggio da parte
del comunicante (gammaC) propongo:

• tipo di conoscenza: teorica, esperienziale, operativa, didattica, culturale;
• tipo di comunicante: v. § 4.2;
• livello di conoscenza;
• qualità di conoscenza.

4.6 Come spunti sull’idea del comunicante dell’oggetto del
messaggio (omegaC) propongo:

• tipo di importanza attribuita all’oggetto: teorica, operativa, formativa, informativa, culturale;
• livello di importanza attribuita all’oggetto;
• tipo di recettore previsto;
• tipo di interesse previsto per il recettore;
• livello di interesse previsto per il recettore;
• difficoltà di comunicazione;
• difficoltà di recezione.

4.7 Come spunti sull’espressione (epsilon) propongo:

• conoscenze del comunicante sull’oggetto:
  • trattazioni disponibili;
  • studi sull’argomento;
  • riflessioni critiche;
• conoscenze del comunicante per il messaggio:
  • tipi di comunicazione;
  • strumenti di comunicazione: stampa, audiovisivi,
  • new media, materiali didattici, internet;
  • tipi di messaggio: v. § 4.8;
  • strumenti per realizzazione: personal computer, scanner,
  • telecamera, laboratorio, teaching machines;
  • canali di diffusione (commerciali, informativi);
  • livelli;
  • eventuali prerequisiti dichiaratamente richiesti al recettore o note esplicative;
  • stili: struttura (tradizionale, ipertestuale, ipermediale, dialogo, intervista), scelte grafiche, scelte linguistiche;
  • studi metodologici (per esempio: “strategia dell’algoritmo” di N. Taddei in http://newrobin.mat.unimi.it/users/lucchini/gl-ntsa.jpg);
• scelte del comunicante:
  • sull’oggetto;
  • sul messaggio.

4.8 Come spunti sul messaggio (m) propongo (oltre a indicazioni di § 4.7):

• tipi:
  • enciclopedie, dizionari, libri, articoli, riviste, numero monografico di rivista, libri di testo, libri per insegnanti, conferenze, relazioni, lezioni, comunicazioni, presentazione, intervista, dialogo, indici, citazioni, file con collegamenti, audiovisivi, programmi
  • multimediali;
  • mostre, musei, festival, realizzazioni scolastiche;
  • gare matematiche;
    • obiettivi: v. § 4.2;
    • livelli;
    • qualità, adeguatezza;
    • data, firma.

4.9 Come spunti sulla diffusione (delta) propongo:

• aspetti tecnici;
• aspetti commerciali;
• aspetti culturali;
• difficoltà tecniche;
• disturbi:
• individuabilità, reperibilità.

4.10 Come spunti sulla lettura (ro) propongo:

• fonti di informazione;
• fonti di orientamento;
• scelta del messaggio
• accesso al messaggio;
• difficoltà di comunicazione [17];
• difficoltà culturali;
• difficoltà psicologiche;
• preparazione alla lettura;
• eventuali prerequisiti richiesti per l’oggetto;
• eventuali prerequisiti per l’uso del medium;
• problema delle comunicazioni perse (elementi presenti nel messaggio, ma non recepiti);
• problema delle comunicazioni inavvertite [18] (elementi recepiti, ma non presenti nel messaggio).

4.11 Come spunti sulla conoscenza del messaggio da parte del recettore (gammaR) propongo:

• comprensibilità del messaggio;
• adeguatezza della lettura;
• riflessioni critiche;
• comunicazioni perse;
• comunicazioni inavvertite.

4.12 Come spunti sull’idea del recettore sull’oggetto del messaggio (omegaR) propongo:

• adeguatezza del messaggio;
• comprensione del messaggio, anche rispetto a comunicazioni perse e comunicazioni inavvertite;
• valutazione critica dell’idea;
• eventuali approfondimenti.

5 Ovviamente, la scuola può essere considerata un riferimento per significativi spunti rispetto alla divulgazione (non soltanto) matematica; propongo:

• scuola come attività di divulgazione (in relazione ai livelli):
  • strutturazioni del sapere;
  • senso del sapere;
  • conoscenze disciplinari;
  • collegamenti tra discipline;
  • quadri di riferimento;
  • libri di testo;
• scuola come preparazione alla conoscenza autonoma, alla lettura, all’approfondimento, all’aggiornamento;
• insegnante come mediatore con programma e libri di testo.

6 In relazione alla disponibilità di una rilevante quantità di materiale divulgativo per la Matematica e alla produzione corrente, particolare importanza ha, qui, la questione di servizi per l’offerta di messaggi o di segnalazioni per l’accesso a fonti di informazione e di orientamento (v. § 4.10), che consentano l’individuazione sia di argomenti e sia di messaggi adeguati alle esigenze, preferibilmente non limitati da scelte (legittime) di linea culturale (o scuola di pensiero) o preferenze su temi, autori, punti di vista.

Come spunti propongo:

• fonti di messaggi;
• servizi di, su, per divulgazione matematica (aperti a contributi datati e firmati, indicazioni e richieste);
• possibilità offerte da internet;
• rischi presentati da internet;
• difficoltà di gestione dell’accumulo di messaggi;
• servizi per la gestione dell’accumulo di messaggi:
  • archivio sistematico di dati;
  • progetto di divulgazione con:
  • itinerari di lettura per livelli,
  • elenchi (argomenti, libri, riviste, articoli, siti, messaggi, recensioni, presentazioni, guide, segnalazioni, inviti alla lettura, indici, citazioni),
  • schede (datate e firmate),
  • aggiornamenti (datati e firmati);
• portale o rivista di riferimento;
• novità e messaggi da salvare;
• sinergie siti, riviste, libri;
• proposte alle scuole;
• problema degli errori.

7 Concludo con l’indicazione di ulteriori spunti e di approfondimenti:

• insuccessi in Matematica;
• difficoltà della Matematica;
• master sulla comunicazione scientifica;
• impact factor;
• indici di leggibilità;
• scuola, divulgazione e cultura;
• Matematica e cultura;
• new media e divulgazione, multimedialità, ipermedialità;
• consultazione “usa e getta” e archiviazione;
• attività del MIUR (programmi, finanziamenti, progetto lauree scientifiche, settimane della cultura scientifica, segnalazioni nei siti internet (www.pubblica.istruzione.it, www.miur.it, …);
• esempi significativi.

Note

[1] Dipartimento di Matematica dell'Università degli Studi di Milano
– gabriele.lucchini@unimi.it
– pagine internet personali
http://newrobin.mat.unimi.it/users/lucchini/gabl00.htm
– ultima revisione: 2009-09-07.
Sarò grato di osservazioni e suggerimenti.

[2] Notizie su N. Taddei sono reperibili in internet; segnalo la mia pagina di riferimento http://newrobin.mat.unimi.it/users/lucchini/l-tadd.htm; sulla comunicazione segnalo la trattazione di N. Taddei in Educare con l’immagine (Roma, CiSCS, 1976, 2 volumi) e http://newrobin.mat.unimi.it/users/lucchini/rp-comn.htm.

[3] Ritengo che alcune variazioni terminologiche e alcune integrazioni non mi abbiano allontanato dalla sua impostazione, anche perché alcune mie proposte sono state da lui accettate, come lo schema di figura 5, al quale ha dato la denominazione nel pubblicarlo sulla sua rivista.

[4] Informazioni sono in http://newrobin.mat.unimi.it/users/lucchini/l-shn0.htm.

[5] Informazioni sul libro sono in http://newrobin.mat.unimi.it/users/lucchini/l-shwe.htm

[6]Recent Contribution to The Mathematical Theory of Communication.

[7] Sugli “arricchimenti” dello schema rimando al testo di N. Taddei
citato in nota 2, limitandomi ad alcuni spunti nelle indicazioni successive.

[8] “Pedagogia delle scienze matematiche fisiche e naturali” all’Università
Cattolica del Sacro Cuore (sede di Brescia); v. L’insegnamento della
Matematica e le nuove metodologie, Milano, La Viscontea, 1977 (p. 49)
e Ferrara, Corso, 19832 (p. 33).

[9] Rispetto a figura 3 ho cambiato il verso delle frecce e usato m per messaggio (invece di s per segno) e omega invece di r.

[10] “Le nuove metodologie didattiche”, EDAV, n. 69 (1979), tavola 7.

[11] Ci sono variazioni di formulazione rispetto alla fonte segnalata in nota 8.

[12] Informazioni sono reperibili in internet; segnalo
http://newrobin.mat.unimi.it/users/lucchini/rp-5w.htm.
Si tenga presente che una variante dello schema era inserita nella sezione
“Esplorare, conoscere, progettare” degli “Obiettivi specifici di apprendimento”
per la scuola dell’infanzia dell’allegato A al decreto legislativo 2004-02-19, n. 59:
9. Adoperare lo schema investigativo del “chi, che cosa, quando, come,
perché” per risolvere problemi, chiarire situazioni, raccontare fatti,
spiegare processi.

[13] Alcune scelte, anche di collocazione in sezioni, sono soggettive; ampliamenti
e spostamenti sono lasciati al lettore interessato.

[14] Sui settori scientifico-disciplinari rimando al DM 2000-10-04 e segnalo
http://newrobin.mat.unimi.it/users/lucchini/s001004.htm.

[15] Interesse per teoremi e risultati, collegamenti culturali, riflessioni critiche;
invito a tenere presenti le citazioni proposte alla fine di questa sezione.

[16] Segnalo il ben noto “il medium è il messaggio” di Marshall McLuhan.

[17] N. Taddei considera “lo jato tra cattedra e banchi, …” (libro citato in nota 2,
p. 12).

[18] N. Taddei considera tre tipi: informazioni alonate, comunicazione di
inesistente, comunicazioni clandestine (libro citato in nota 2, pp. 156-157).

di Gabriele Lucchini [1]