Teoria dei giochi: una scienza bambina

La teoria dei giochi è una disciplina matematica neonata. La sua nascita, infatti, viene convenzionalmente fissata con l’uscita del famoso libro di Von Neumann-Morgestern, Theory of Gamesand Economic Behavior (Princeton University Press, 1947). Se confrontiamo questa data con quella della nascita della geometria o della fisica, ne concludiamo appunto che stiamo parlando di una scienza bambina. Ha dunque tutti i pregi ed anche, forse, i pochi difetti di una giovane creatura. In particolare, ha in sé interessi e potenzialità straordinari. Il suo interesse risiede, secondo me, in un suo aspetto bifronte: da una parte ha applicazioni notevoli, interessanti, nuove: è una disciplina pratica. Dall’altra è invece capace di proporre, in maniera originale, questioni profonde, che si legano ad altre discipline e non solo, ma anche agli aspetti più importanti del pensiero umano. Certo, anche la matematica pura ha aspetti che interessano i filosofi della scienza: pensiamo al teorema di Gödel. Provate però a spiegare questo teorema ad una persona pur curiosa e sveglia, ma senza una cultura (universitaria) matematica: temo ci sarebbero non poche difficoltà. Invece la teoria dei giochi pone problemi semplici, per esempio sul concetto di razionalità, che tutti possono intuire, anche senza solide basi matematiche. Un celebre esempio: il dilemma del prigioniero, modello di situazioni che si pongono mille volte alla nostra attenzione, ma che solo attraverso la sua matematizzazione si è chiarito in termini precisi.
Certamente è arbitrario tentare di ingabbiare la teoria in un certo numero di schemi e capitoli fondamentali: ancor più che lo faccia io. Tuttavia si può suddividerla in un certo numero di grandi filoni.

La prima suddivisione si può fare distinguendo fra giochi non cooperativi e giochi cooperativi. È importante osservare da subito che questo non significa che in quelli cooperativi si aspettano atteggiamenti più altruistici da parte dei giocatori: questo non si assume mai, perché l’ipotesi base è che ognuno persegue il suo interesse (se poi il tuo interesse consiste nel fare del bene al prossimo, ciò risulta dal tuo grado di soddisfazione nel fare una cosa piuttosto che un’altra; il punto chiave rimane che fare del bene soddisfa te, e questo è ciò che guida le tue azioni). La teoria cooperativa studia il formarsi di coalizioni appunto perché queste possono essere di vantaggio ai singoli componenti. La teoria non cooperativa cerca invece di spiegare i meccanismi delle decisioni dei singoli, sulla base di ragionamenti individuali, senza alleanze fra individui. Si deve soprattutto a Von Neumann l’idea di analizzare i giochi studiando il nascere delle coalizioni fra individui, mentre è Nash che ha dato impulso alla teoria non cooperativa (suscitando le critiche di von Neumann, del resto).

Un’altra divisione possibile fra giochi riguarda la loro descrizione in forma matematica. Si parla allora di giochi in forma estesa e di giochi in forma normale (o strategica). Nella prima categoria mettiamo la descrizione del gioco sotto forma di albero: si tratta di costruire un grafo che, partendo dalla radice, descrive il gioco mossa per mossa, fino ad arrivare a presentare tutte le situazioni finali, conseguenti ad una data serie di mosse. Il tutto fornisce un modo estremamente efficace ed esauriente per analizzare un gioco, ma ha il difetto di essere molto complicato. Guardate che succede per un gioco semplice (e piuttosto pericoloso), come il seguente:
Descrizione del gioco:
Stato iniziale: 2 giocatori e una rivoltella a sei colpi, con un colpo solo nel tamburo.
Evoluzione: ogni giocatore mette 10.000 lire nel piatto, per aver diritto a partecipare al gioco. Se il giocatore che deve muovere per primo decide di passare, mette 20.000 lire nel piatto. Se invece decide di portare la pistola alla tempia, aggiunge altre 10.000 lire al piatto e poi preme il grilletto. Se sopravvive allo sparo, passa la pistola al secondo, (dopo aver rigirato il tamburo), che ha le stesse possibilità.
Stato finale: sopravvivenza o meno dei giocatori.
Risultato: se entrambi sono vivi, si dividono il piatto; se sono morti il piatto è perso; se (solo) uno sopravvive, il piatto è suo.
La struttura ad albero del gioco è descritta nella figura seguente, dove in ogni situazione finale è riportato il corrispondente guadagno del primo giocatore.

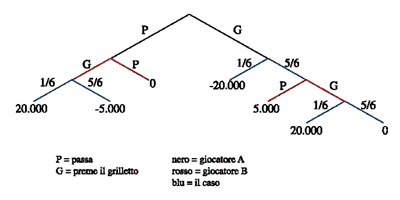
Osservate che in questo gioco ogni giocatore fa al massimo una mossa…figuratevi costruire un albero completo per giochi con un grande numero di mosse!
Comunque dall’albero di sopra l’esperto della teoria è in grado di determinare il comportamento di due giocatori razionali, senza soverchia fatica. Senza spiegare perché, vi dico che ambedue sparerebbero; se vi sorge allora il dubbio che l’esperto sia fuori di testa, posso rassicurarvi invece che ha fatto i conti giusti, a condizione che l’utilità dei giocatori sia descritta correttamente dal loro guadagno (e questo si che è opinabile, ma allora i giocatori dovrebbero specificargli come valutare le loro utilità).
La forma strategica invece di solito precisa il numero dei giocatori, lo spazio delle loro strategie, e la funzione di utilità di ciascuno di essi: una funzione a valori reali, definita sul prodotto cartesiano degli spazi di strategie. Ecco, il punto fondamentale è forse nel fatto che le strategie in questa descrizione sono un dato del problema, mentre nella forma estesa abbiamo serie di mosse, ed un compito delicato di chi analizza il gioco è proprio quello di dedurne da queste le strategie di ogni giocatore.
Un’altra importante distinzione è quella fra giochi ad informazione completa e quelli ad informazione incompleta. Potremmo anzi dire che i primi sono un primo passo verso una teoria più sofisticata ma anche più soddisfacente, perché propone modelli più aderenti alla realtà. In effetti, quando studiamo un fenomeno, ad esempio economico o biologico, quasi mai tutte le informazioni sono parimenti note a tutti i protagonisti. Pertanto un modello che tenga conto di questo fatto appare più verosimile.

Ma vediamo, su un esempio, che tipo di problemi potrebbe proporsi di analizzare la teoria dei giochi, e come li affronta. Ho scelto di presentare, rapidamente, il modello di contrattazione di Nash. L’idea è quella di suggerire ad un certo numero di persone che devono ad esempio spartirsi una somma, il modo più razionale di farlo. In altre parole, il teorico dei giochi deve proporre un modello che suggerisca come comportarsi, in ogni circostanza, in modo da proporre una soluzione “accettabile” per tutti.
Cominciamo da un esempio “pratico”.

Due persone devono spartirsi la somma di 500 euro. Esse sono una ricca e l’altra povera.
L’utilità u di una somma di denaro x per una persona ricca può essere espressa convenzionalmente dalla funzione:
u(x) = c·x
(c > 0, piccolo)
Chiamiamo invece v l’utilità del denaro per la persona povera, quella che possiede solo 100 euro, rappresentata dalla seguente funzione: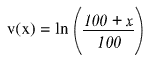



Le funzioni di utilità possono essere spiegate così:
La persona ricca ha un aumento di soddisfazione lineare rispetto alla somma che ottiene, perché possiede molto, quindi per lui avere qualcosa in più non cambia in modo sostanziale la sua vita: se gli date 100 la sua soddisfazione è 100c, se gli date 200, la sua utilità semplicemente raddoppia.
La persona povera, invece, ha una grande soddisfazione da principio, quando comincia a ottenere un po’ di più di quel che ha, ma poi ha un atteggiamento quasi d’indifferenza, rispetto a possibili aumenti di guadagno.

Tornando al nostro gioco, se al primo giocatore spetta la somma y, il secondo giocatore rimarrà con la somma di 500 – y, quindi dalle due relazioni espresse precedentemente si ottiene: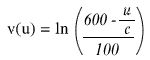



Rappresentiamo questa relazione nel piano u, v: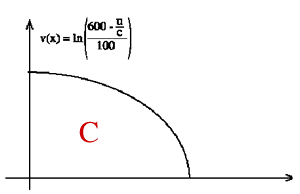



La curva ottenuta rappresenta la funzione scritta sopra. Noi però supponiamo che tutti i vettori (u, v) che stanno nella regione C fra gli assi e la curva siano distribuzioni possibili: questo è molto comodo dal punto di vista matematico, perché C risulta essere un insieme convesso (il che aiuta molto per ottenere certi risultati) e corrisponde, nel modello, al fatto, non del tutto irrealistico, che i due che contrattano possono decidere di buttare via un po’ di utilità possibile (almeno se non stanno sul bordo curvilineo della regione C).
In questo specifico esempio Nash propone dunque, con il suo modello, di assegnare
310 euro al primo giocatore, 190 euro al secondo.
In realtà Nash non si è certo posto la precedente questione, ma ha costruito un modello. Come?

Un modello di contrattazione a due giocatori è contraddistinto da un insieme (chiuso e limitato) convesso del piano, che indichiamo con la lettera C, e da un punto x del piano, che in genere sta all’interno dell’insieme C. Quest’insieme C rappresenta i livelli di utilità raggiungibili dai giocatori, in caso di accordo.
Cioè se z = (z1, z2) appartiene a C, allora vuole dire che è possibile una situazione in cui il primo giocatore ottiene qualcosa che valuta z1, e il secondo qualcosa che valuta z2 .
Il punto x = (x1, x2) invece rappresenta l’utilità dei due giocatori nel caso non ci sia accordo (in genere, come nell’esempio precedente, si può assumere x = (0, 0).
La soluzione, secondo Nash, sarà dunque una funzione f che a ogni coppia (C,x) come sopra assegna, in un dato modo, un elemento z = f(C, x) appartenente a C. Nash propone che questa funzione, qualunque siano C ed x, soddisfi a certi requisiti che si ritengono ragionevoli. Lui suggerisce i seguenti:
Indicando allora con f((C, x)) la soluzione che si auspica per il gioco (C, x), e ricordando che
f((C, x)) è un vettore a due componenti, che indicano rispettivamente l’utilità del primo e del secondo giocatore, allora f((C, x)) deve soddisfare:

Condizione 1 - Sia dato (C, x) e supponiamo sia (C’, x’) ottenuto da (C, x) in questo modo.
Dati h, k > 0 e a, b numeri reali, si ha che x’=(hx1 + a, kx2 + b) e ogni elemento y di C’ si scrive come (hz1 + a, kz2 + b) con z = (z1, z2) in C.
Allora f((C’, x’)=(hf1((C, x) + a, kf2(C, x) + b).

Condizione 2 - Sia (C, x) tale che x = (u, u) e se z = (z1, z2) appartiene a C allora anche w = (z2 , z1) appartiene a C.
Allora f1((C, x)) = f2((C, x)).

Condizione 3 - Se (C, x) e (C’, x) sono tali che C’ contiene C e f((C’, x)) appartiene a C,
allora f((C, x)) = f((C’, x)).

Condizione 4 - Se esiste in C un elemento z con tutte e due le componenti maggiori di y,
allora f((C, x)) non può essere y.

Consideriamo allora la classe C di tutti i giochi (C, x) con C chiuso convesso limitato, x in C, e tali che esiste y =(y1 , y2) in C con y1 > x1, y2 > x2.

Allora:
TEOREMA DI NASH
Esiste un’unica funzione f definita su C e che soddisfa i 4 assiomi precedenti.
Essa si ottiene massimizzando su C la funzione:
g(u, v)=(u – x1)(v – x2).

Dunque il teorema di Nash è in grado di mettere d’accordo chiunque si trovi in una situazione come quella di sopra ed accetti le sue condizioni per un’equa spartizione.
Per concludere, un breve commento sulle condizioni precedenti (per vedere se anche voi sareste d’accordo con Nash).

Il primo assioma è detto d’invarianza rispetto a trasformazioni di utilità. In pratica dice che se cambiamo unità di misura all’utilità del giocatore (i fattori h e k) e aggiungiamo certe quantità iniziali (partendo dalle utilità a e b, per esempio, invece che 0 e 0), il risultato cambia tenendo conto esattamente dei fattori precedenti. Insomma non cambia, in sostanza, il risultato se lo si esprime in lire o in dollari (pur di esprimerlo sempre in lire o in dollari) e cambia delle stesse quantità se spostiamo i livelli zero di utilità.

Il secondo, detto assioma di simmetria, è molto chiaro: significa che in un gioco simmetrico il risultato deve essere simmetrico. Se i giocatori sono indistinguibili dal punto di vista delle loro utilità e dal punto di partenza, il risultato dev’essere lo stesso per ambedue.

Il terzo è chiamato indipendenza dalle alternative irrilevanti: se aggiungere a C, che è l’insieme delle utilità che i giocatori si possono garantire nella contrattazione, altri elementi, che portano a costruire un insieme più grande C’, porta come risultato a una situazione che già era in C, allora quest’ultima è già la soluzione per il gioco C. (Notare che il punto di disaccordo è lo stesso in entrambi i giochi). In altre parole, quello che abbiamo aggiunto a C non sono che alternative irrilevanti, appunto.

Infine l’ultimo assioma vuol mettere in luce un criterio di efficienza: non ha senso accontentarsi di un risultato, se entrambi i giocatori possono fare meglio. Dunque, anche ammettendo che i giocatori possano distruggere utilità, questo non può accadere all’equilibrio..

Concludo osservando, a proposito dell’esempio della suddivisione degli euro, che probabilmente non sareste contenti, se siete la persona povera, di quel che propone Nash, pur ammettendo che le sue condizioni sono ragionevoli. Che fare allora? In fondo, il risultato dipende dalle funzioni di utilità dichiarate. Ed allora, conoscendo il teorema di Nash, che cosa vi spinge a dichiarare una funzione di utilità logaritmica come quella di sopra? Proprio nulla, e questo introduce il problema della veridicità delle dichiarazioni, e di conseguenza dell’informazione incompleta.

Le figure e alcune parti dell'articolo sono tratte dal libro dell'autore "Di duelli, scacchi e dilemmi . La teoria matematica dei giochi" edito da Paravia Bruno Mondadori Editori.