Un contributo alla discussione sui sistemi economici
Spesso si legge di una insufficiente crescita del prodotto interno lordo, ma può un sistema continuare a crescere indefinitamente? Nella realtà si creano dei periodici cicli economici che vedono una decrescita alternata alla crescita. Allora – e questa vuol essere la tesi di questo articolo – più che alla crescita indefinita, bisognerebbe puntare alla stabilità del sistema economico, ovvero a uno sviluppo regolamentato (oltre che sostenibile). Possiamo azzardare un confronto tra un modello elettronico e uno economico. Le conclusioni saranno alquanto immediate, vista la semplicità del modello che andremo a considerare, tuttavia, può essere utile fare qualche considerazione sulla stabilità dei sistemi quale contributo per alcune riflessioni. Se si continua a incrementare il segnale di ingresso a un amplificatore, a un certo punto il segnale di uscita tenderà a non aumentare ulteriormente, anzi comincerà a diminuire: si dice che l'amplificatore è in saturazione. Si può già fare un paragone con quelli che sono i cicli economici. Ai fini della nostra discussione, senza entrare in eccessivi dettagli matematici, ricordiamo che le reti possono essere schematizzate attraverso delle funzioni di due variabili1. Una delle variabili indica il loro comportamento in frequenza2, l'altra è legata alla stabilità del sistema stesso. Le due variabili sono indicate con ω e α, in particolare espresse attraverso il numero complesso s dato da:
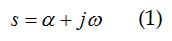
Un esempio di una tale funzione potrebbe essere:
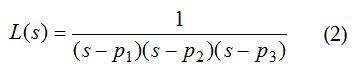
Nella (2) p1, p2 e p3 si definiscono poli del sistema. Affinché un sistema sia stabile deve avere poli a parte reale negativa. In particolare si verificano 3 casi:
a) il sistema presenta poli a parte reale negativa: sistema stabile;
b) il sistema presenta poli a parte reale positiva: sistema instabile;
c) il sistema presenta poli a parte reale nulla: sistema al limite di stabilità.
In base a queste precisazioni possiamo ora schematizzare il singolo amplificatore attraverso un modello del tipo:
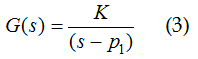
Nella (3) se la parte reale del polo, p1, tende a zero, pur rimanendo negativa, si ha un rischio di instabilità laddove dovessero intervenire variazioni esterne. Questo modello, leggermente aggiustato per gli scopi della nostra discussione, serve a schematizzare un sistema che, come si dice è al limite della stabilità. Ebbene per stabilizzare questo sistema, ovvero per aumentare il suo margine di stabilità, si utilizza uno schema a controreazione negativa, come in fig.1.
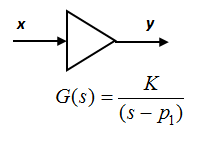
Fig.1a Amplificatore singolo
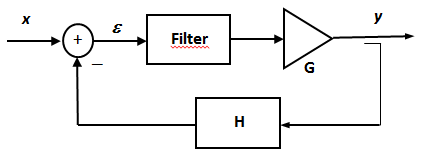
Fig.1b Amplificatore controreazionato
Lo schema in fig.1b può sembrare alquanto complesso, ma non si sta facendo altro che riportare in ingresso una parte del segnale di uscita, cosa che può stabilizzare il sistema. Matematicamente ciò si può verificare subito, poiché si vedrà che i poli del sistema in fig.1b non solo hanno ancora parte reale negativa ma, inoltre, si sono allontanati dall'asse immaginario (cioè dallo zero), il che, appunto, aumenta il margine di stabilità. Matematicamente in base alla fig.1b si ha:
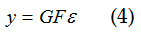
ovvero:
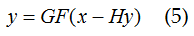
dalla (5) si ha:
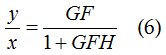
Dalla (6) in base alla (3) si ottiene:
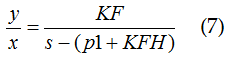
Come si vede, il polo di questa funzione non è più in p1 ma è in p1+KFH, quindi la sua parte reale è incrementata della quantità KFH allontanandosi dall'asse immaginario, il che appunto, ne aumenta il margine di stabilità. Nel sistema di fig.1b, è fondamentale che la reazione sia, come si dice in gergo, negativa, ovvero che ci sia un segno meno nel nodo sommatore. Se ε invece di essere ottenuto come:
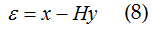
fosse invece ottenuta come:
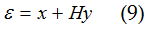
il sistema sarebbe definito a reazione positiva e diventerebbe instabile (visto che il polo in p1–KFH tenderebbe a diventare a parte reale positiva). Quindi la controreazione negativa contribuisce a migliorare la stabilità di un sistema. Il miglior margine rispetto alla stabilità consente anche di gestire possibili variazioni nei parametri, ovvero consente di mantenere in stabilità anche un sistema che, per effetti esterni, abbia una variazione nei parametri tale da portare la parte reale dei poli verso valori positivi. Inoltre gli stessi parametri F e H possono essere resi variabili, adattandoli a situazioni dinamiche. Un'altra situazione di possibile instabilità si può verificare quando si introduce una linea di ritardo nel percorso di retroazione. Senza entrare nei dettagli matematici ciò equivale a modificare le relazioni di fase tra i segnali x e Hy in un modo tale che la controreazione non avvenga esattamente in controfase. Fatte queste considerazioni sul modello elettronico, possiamo tentare un paragone con un sistema economico dicendo che il modello espansivo, che tende ad incrementare il parametro K, o in modo equivalente a ridurre la parte reale dei poli, deve essere moderato attraverso un feedback negativo che sia proporzionale all'incremento stesso. Il modello conferma, quindi, l'opportunità di politiche macroeconomiche che superino il mero equilibrio tra domanda e offerta. Oltre a politiche monetarie, come il controllo dei tassi e il prelievo fiscale3, pur rimanendo in un sistema liberale, sarebbe auspicabile prevedere un aggiornamento e un potenziamento delle politiche Keynesiane. Senza arrivare a politiche protezionistiche, potrebbe essere possibile un intervento da parte degli Stati anche nel controllo dei prezzi per salvaguardare entità e attività locali. Si è, inoltre, osservato che non bisogna introdurre ritardi eccessivi sulla catena di controreazione. Queste sono considerazioni molto elementari, ma servono evidenziare l'opportunità di un intervento sul sistema per una sua regolamentazione.
NOTE
1. C.A. Desoer, E.S. Kuh, "Basic Circuit Theory", McGraw-Hill 1969.
2. Per esempio un amplificatore stereo avrà un buon guadagno nell'ambito delle frequenze audio, ma via via decrescente a frequenze più alte.
3. Parlando di gettito fiscale viene, poi, spontaneo evidenziare i seguenti punti:
1) la tassazione dovrebbe essere proporzionale al reddito;
2) la tassazione dovrebbe riguardare tutti i cittadini;
3) il gettito fiscale dovrebbe essere reinvestito dallo Stato, per promuovere le stesse attività economiche.
