Un linguaggio per la programmazione matematica

1. Premessa

Questo documento ha l'obiettivo di illustrare come utilizzare il programma Xpress–MP per costruire e risolvere dei modelli di programmazione lineare anche in ambiti professionali.

Il programma è disponibile anche in versione studente.

Gli ambiti di applicazione della versione studente (gratuita) sono sufficientemente ampi da consentire la progettazione di modelli utilizzabili anche in ambito aziendale.

Essi sono:

•  vincoli (righe) = 400

•  variabili (colonne) = 80

•  elementi matrice = 5000

•  variabili binarie = 400

E' richiesta la registrazione per ottenere la password per l'utilizzo del software; il manuale di uso e molti esempi di modelli applicativi sono ugualmente scaricabili. Dopo la registrazione si riceve una email:

Thank you for downloading Xpress-IVE (student license). Please note that this software is only for use by students in full-time or part-time education studying for a recognized qualification.

To install the software, please extract the installation kit from the zip archive you have downloaded. You will be asked for a password, which is:

studentonly

The Getting Started manual tells you how to use Xpress-MP. For a complete language reference, please refer to the Mosel Reference Manual.....

Il vantaggi principali di XPRESS sono quelli di:

•  rappresentare il modello di programmazione lineare in forma matematica con ampio utilizzo di riferimenti sintetici e simbolici a matrici e a vettori;

•  separare la logica del modello dai dati di ingresso, rendendo il modello applicabile anche a dati di input con diversa numerosità delle variabili interessate;

•  integrare nel modello filtri e condizioni particolari di calcolo;

•  scegliere le modalità di rappresentazione dei risultati e dei formati di output.

2. Contenuti

Il documento contiene una concisa e facile introduzione alla modellistica e alla risoluzione dei diversi tipi di ottimizzazione con Xpress-MP.

Sono trattati problemi di Programmazione lineare, di Programmazione a variabili miste e di Programmazione quadratica, tutti risolti attraverso l'utilizzo di un programma ad interfaccia grafica di nome Xpress-IVE.

Sono disponibili due alternative:

•  utilizzare un linguaggio di programmazione che utilizza una libreria di costruzioni dei modelli di nome Xpress BCL;

•  inserire direttamente l'input in Optimizer in forma di matrice.

In questo documento sono illustrate delle variazioni di un unico problema che si riferisce alla scelta di un portafoglio titoli.

Chi fosse interessato ad altri tipi di applicazione, può consultare ‘Applications of Optimization with Xpress-MP' (Dash Optimization, 2002), vedere anche:

http://www.dashoptimization.com/applications_book.html

Questo documento mostra come formulare e risolvere un ampio numero di problemi di programmazione matematica con Xpress.

Altra documentazione (guide utente, manuali di riferimento, linguaggio Mosel, moduli Mosel, suggerimenti di modellistica, ecc.) è disponibile nel sito già citato.

3. Programmazione matematica

La Programmazione matematica è una tecnica di ottimizzazione matematica.

Molti problemi nella vita reale, ad esempio nella produzione industriale, nei trasporti, nelle telecomunicazioni, nelle finanze, nella pianificazione delle risorse, possono essere espressi in modelli di Programmazione Matematica composti da insiemi di variabili di decisione e di funzione obiettivo da massimizzare o da minimizzare.

I problemi di Programmazione matematica sono usualmente classificati nell'ambito della Programmazione lineare, quando tutti i vincoli e la funzione obiettivo sono espressioni lineari delle variabili di decisione e quando le variabili possono assumere dei valori continui.

Altre volte le variabili continue non sono adatte a rappresentare decisioni di carattere discreto (sì/no oppure 1,2,3,...) e allora vengono in aiuto gli algoritmi Mixed Integer Programming (MIP) nei quali i vincoli e la funzione obiettivo sono lineari (come nella Programmazione lineare) mentre le variabili possono assumere sia valori continui sia valori discreti.

Per risolvere problemi di questo tipo, le tecniche di Programmazione lineare sono accompagnate da quelle di tipo enumerativo (conosciute come Branch-and-Bound ) per la ricerca dei valori discreti ammissibili.

I metodi di tipo enumerativo possono comportare tempi esagerati di calcolo anche per problemi relativamente modesti, impedendo di fatto la soluzione ottimale dei modelli di tipo MIP.

Negli ultimi anni, il continuo miglioramento della velocità dei computer e degli ancora più significativi progressi negli algoritmi (ad esempio, tecniche del cutting plane e specialized branching schemes ) hanno reso possibile gestire problemi sempre più complessi e rappresentativi di problemi reali.

Altre categorie di problemi relativamente ben gestiti sono rappresentate dalla Programmazione quadratica (QP), problemi che differiscono da quelli della Programmazione lineare per il fatto che hanno termini quadratici nella funzione obiettivo (mentre i vincoli restano lineari).

Le variabili di decisione possono essere sia continue sia discrete; in quest'ultimo caso si parla di Mixed Integer Quadratic Programming (MIQP)

E' molto difficile gestire i problemi con vincoli non lineari (NLP) Non-linear Programming .

Frequentemente sono impiegati metodi euristici o approssimativi per trovare buone soluzioni (ottimi locali). Un metodo per risolvere problemi di questo tipo è Successive Linear Programming (SLP) che è anche una tecnica di soluzione compresa nei programmi di Xpress-MP.

Comunque in questo documento non ci sono approfondimenti su questa tecnica.

Costruire un modello, risolverlo e poi applicarlo al mondo reale, non sono attività che si svolgono in modo lineare.

Si fanno spesso degli errori nella fase di modellazione che vengono rilevati solo dal processo di modellazione (esempio modello unbounded oppure infeasible ) oppure che sono in contrasto con una nostra ferma intuizione. Quando ciò accade siamo obbligati a riflettere sul modello, aggiornarlo, ricalcolarlo ed analizzare nuovamente i risultati ottenuti. Nel corso di questo processo è normale aggiungere dei vincoli, togliere vincoli non opportuni, correggere dati errati, inserire nuovi dati prima ritenuti non necessari.

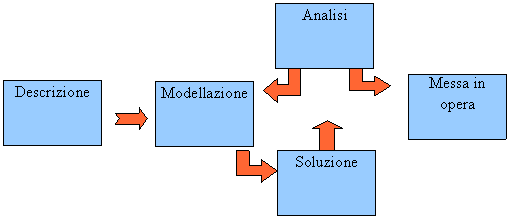
Questo documento accompagna il lettore nel percorso:

•  dalla descrizione testuale allo sviluppo di un modello matematico da risolvere;

•  proposte di diversi miglioramenti, aggiunte e riformulazioni nei capitoli successivi;

•  esame dei mezzi disponibili per analizzare i risultati ottenuti.

E' possibile approfondire gli strumenti di modellazione e vedere quattro esempi di applicazione (la definizione di un portafoglio di investimenti, la formulazione ottimale di una ricetta attraverso la "Matematica del biscotto", la programmazione della produzione e la pianificazione di una campagna pubblicitaria di banner su web) scaricando l'intero documento.