A un mese dalla scomparsa di Leonid Shilnikov pioniere della teoria delle biforcazioni omocline

Leonid Pavlovich Shilnikov, uno dei più influenti studiosi della teoria qualitativa dei sistemi dinamici e creatore della teoria delle biforcazioni omocline in sistemi a molte dimensioni, è morto il 26 dicembre 2011 all'età di 77 anni.

La sua carriera accademica si è svolta interamente a Nizhny Novgorod (chiamata Gor'kij dal 1932 al 1991) in cui era il direttore della prestigiosa scuola di sistemi dinamici, nata dal famoso gruppo di Andronov che negli anni ’30 ha introdotto l’idea di stabilità strutturale, ponendo le basi della moderna teoria delle biforcazioni. Shilnikov ha sviluppato, ampliato e applicato i loro metodi diventando uno dei nomi più citati in articoli e testi sui sistemi dinamici e caos deterministico degli ultimi trent'anni. Un simpatico aneddoto racconta che al convegno internazionale "Progress in Nonlinear Science", svoltosi a Nizhny Novgorod nel 2001 per ricordare il centenario della nascita di Andronov, il Bernold Fiedler dell'Università di Berlino disse: "Se prendete un libro sui sistemi dinamici e non trovate citate nella bibliografia opere di Shilnikov buttatelo nel cestino, tanto non ci troverete niente di buono".

Ricordiamo che con il termine "biforcazione" si intende un cambiamento qualitativo (o topologico) nella struttura degli attrattori di un sistema dinamico causato dalla variazione di un parametro che compare nelle equazioni che lo rappresentano (equazioni differenziali o alle differenze). Dopo che le principali biforcazioni dei sistemi dinamici bidimensionali erano state studiate e classificate da Andronov e Leontovich in una serie di articoli e libri pubblicati negli anni '30, Shilnikov ha intrapreso l'arduo compito di estendere questi risultati a sistemi di dimensione maggiore (ovvero a sistemi a tre o quattro dimensioni) ottenendo scenari completamente nuovi e talvolta lontani dall'intuizione. Il passo è stato notevole, anche perché in sistemi dinamici a tempo continuo a dimensione maggiore di due compare il fenomeno del cosiddetto caos deterministico. E infatti è stato proprio Shilnikov, in contemporanea all'americano Steve Smale, a indicare e classificare gli scenari dinamici più tipici per l'insorgere di dinamiche caotiche.

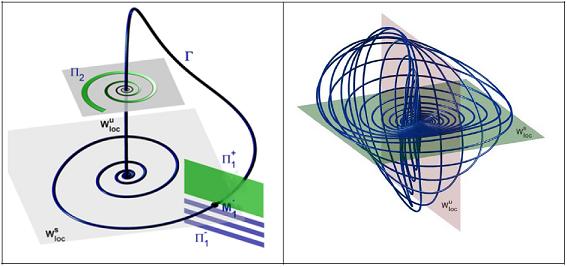
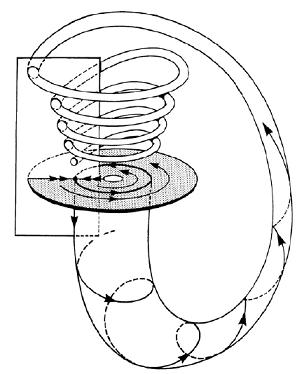
Intorno agli anni '50 Shilnikov iniziò il suo programma sistematico di studio delle biforcazioni in spazi di dimensione maggiore di due e nel 1965 scoprì un nuovo fenomeno dinamico di importanza fondamentale: l'esistenza in un sistema dinamico multidimensionale di un'orbita omoclina associata a una sella-fuoco può portare alla creazione di un insieme infinito di orbite periodiche. Questo risultato è ora noto come "caos (o scenario) di Shilnikov" ed è considerato una pietra angolare della teoria del caos nell'ambito dei sistemi dinamici deterministici. Questa scoperta di Shilnikov comparve nella letteratura poco dopo l'altrettanto nota teoria del "ferro di cavallo" di Smale.

Orbita omiclina di una sella-fuoco (a sinistra). Sella-doppio fuoco omoclina (a destra)

Un principio che stava alla base della scuola dinamica delle oscillazioni non lineari di Andronov era costituito da una costante attenzione alle applicazioni. I principali studi sulla stabilità e la conseguente definizione del concetto di stabilità strutturale presero l'avvio dallo studio di casi concreti tratti da problemi di meccanica, controllo ottimo, cibernetica, aeronautica e missilistica. Questo è stato anche lo stile di lavoro di Leonid Shilnikov, da molti definito approccio "non assiomatico", che ottiene i teoremi partendo da semplici esempi concreti che ne giustificano le ipotesi in modo intuitivo e geometrico. I lavori di Shilnikov sono sempre ricchi di schizzi e figure qualitative per aiutare l'intuizione del lettore a dominare le astratte argomentazioni che stanno alla base delle dimostrazioni in spazi multidimensionali.

Nel 1995 Shilnikov, in un articolo con Turaev, dimostrarono l'esistenza di un nuovo tipo di biforcazine chiamata “blue sky catastrophe”, cioé "biforcazione del cielo azzurro", partendo da un problema proposto da Palis e Pugh nel 1975 (il Problema 37) riguardante le biforcazioni di un'orbita periodica il cui periodo e lunghezza diventano infiniti avvicinandosi al valore di biforcazione del parametro. Esempi di orbite di periodo infinito con lunghezza finita erano già note, ma Shilnikov e Turaev dimostrarono in una particolare biforcazione omoclina con una condizione aggiuntiva che la rendeva di tipo realmente nuovo: l'orbita periodica coinvolta sta lontana dai punti di equilibrio ed è caratterizzata da una lunghezza che cresce all'infinito in rapporto al periodo. Lo studioso americano di sistemi dinamici Ralph Abraham descrisse questo tipo di biforcazione dicendo che è come se l'orbita scomparisse nel cielo azzurro ("in the blue-sky") da cui il nome (catastrofe è spesso usato come sinonimo di biforcazione).

Disegno tratto dall' articolo di Shilnikov e Turaev (1995) sulla "blue sky catastro phe"

Ricordiamo anche la relazione presentata da Shilnikov a Urbino nel 1996, in occasione del convegno ECIT (European Conference on Iteration Theory), nella quale descrisse questo nuovo tipo di biforcazione come assoluta novità. Molti dei presenti ne furono affascinati, dato che per quasi tutti era la prima volta che la sentivano esporre e per di più con i bellissimi schizzi qualitativi disegnati a mano da Shilnikov. In quella occasione avrebbe dovuto essere presente anche Ralph Abraham, che si era già iscritto per presentare una relazione ma che all'ultimo momento fu costretto a rinunciare per un imprevisto. Sarebbe stato certamente un bel confronto.

L. Gardini, L. Shilnikov, A. Shilnikov a Urbino nel 1995

L. Shilnikov, L. Gardini, A. Shilnikov, I. Sushko, T. Kapitaniak, V. Maistrenko, G.I. Bischi al convegno ECIT, Urbino 1996

Shilnikov, che nel 1967 Shilnikov risolse il problema classico di Poincare Birkhoff sul comportamento di un sistema dinamico in un intorno di un'orbita omoclina trasversale, lascia la moglie, una figlia, il figlio Andrey (anche lui matematico all'Università di Berkley in California) e una folta schiera di allievi tra cui N.K. Gavrilov, V.S. Afraimovich, A.D. Morozov, L.M. Lerman, L.A. Belyakov, V.V. Bykov, V.I. Lukyanov, S.V. Gonchenko, M.I. Malkin, N.D.V. Turaev.

L.P. Shilnikov, D.V. Turaev e S.V. Gonchenko a Berlino nel 2004