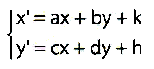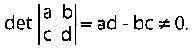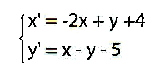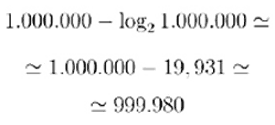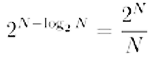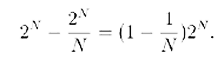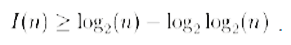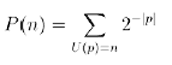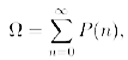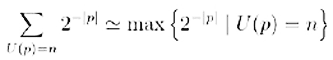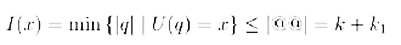Una chiacchierata sulla teoria algoritmica dell'informazione
Prologo
| B.-Ciao, come ti va la vita all’Università? |
A.-Ma... le lezioni sono abbastanza noiose...
B.-Allora facevi meglio a restare al Liceo. |
A.-Però si incontrano persone interessanti e si parla di molte cose, anche fuori dei corsi ufficiali Per esempio, parlando con alcuni compagni e con i professori, ho scoperto una teoria molto interessante che risponde anche ad alcune questioni filosofiche che ti dovrebbero interessare.
| B.-E qual è questa teoria? |
A.-Si chiama teoria algoritmica dell’informazione.
| B.-Che nome complicato. |
A.-Il nome è complicato ma i fondamenti della teoria sono abbastanza semplici.
B.-Ma io la posso capire? |
A.-Sì, se hai un po’ di pazienza.
B.-Allora spiegamela.
Cos'è il caso 2.1. L’indovinello A.-Va bene. Te la spiego con un indovinello. Considera queste due stringhe:
A.-Non fare lo spiritoso. Sai bene che oggi si usa la parola “stringa” per denotare una successione finita di 0 e di 1. È una brutta traduzione della parola inglese string ma, con tutti questi computer che girano, ormai è entrata a fare parte della lingua parlata.
A.-Non divagare e rispondi alla mia domanda.
2.2. Complessità
A.-Se la mia domanda è demenziale, lo è di più la tua risposta perché non mi hai dato alcuna motivazione.
A.-Ma anche la seconda stringa potrebbe avere una regola nascosta. Per esempio si potrebbe ottenere con la seguente regola: prendi il decimo numero primo; sommaci la mia età; inverti l’ordine delle cifre e sommaci 7, se il numero è pari, o moltiplicalo per 8 se il risultato è un numero dispari; converti il numero ottenuto in notazione binaria e così, alla fine, otterrai la stringa S2. Sei sicuro che la seconda stringa non segua questa regola?
A.-Neanche io, ma posso sostenere senz’altro che la stringa S2 segue certamente qualche regola nascosta perché, essendoci infinite regole, può senz’altro essere ottenuta mediante alcune di loro.
A.-Bravo! Hai fatto centro... basta che tu mi definisca quando una regola si dice semplice.
A.-E chi ti dice che la S2 non segua una regola che io ho capito subito quando l’ho scritta?
A.-In questo modo hai semplicemente cambiato nome ai termini del problema. Hai sostituito la parola complessità alla parola casualità. Possiamo convenire che casualità e complessità siano concetti strettamente collegati, ma non hai risposto alla mia domanda iniziale. Se ti fa piacere, ti riformulo la domanda con i termini che preferisci: quale delle due stringhe S1 e S2 è più complessa?
2.3. Probabilità A.-Ti voglio aiutare. Una di queste stringhe l’ho prodotta con questa moneta. L’ho lanciata in aria per 40 volte e ho scritto “1” quando mi è venuto testa, “0” quando mi è venuto croce. Questa informazione ti aiuta? Sai dirmi quale delle due stringhe S1 e S2 è stata prodotta con il metodo del lancio di una moneta?
A.-Perché?
A.-Oppure potrei avere avuto molta fortuna...
A.-Ammetto che la S2 è stata prodotta con il metodo del lancio di una moneta, ma tu non mi hai ancora risposto alla domanda iniziale.
A.-Veramente hai risposto ad un’altra domanda: quale delle due stringhe è stata prodotta casualmente, non quale è casuale.
A.-Non è vero. Non lo potrai mai provare. Lancia questa moneta e vediamo se ti viene la stringa S2.
A.-Da questo punto di vista le due stringhe sono equivalenti. Ognuna di loro ha la probabilità di essere prodotta con lanci casuali di uno su 1 trilione e 99 miliardi 511 milioni 627 mila 776.
A.-Non divagare. Non hai ancora risposto alla mia domanda per almeno due motivi: voglio sapere se una delle due stringhe possa ritenersi casuale in se stessa e non per il modo in cui è stata prodotta; inoltre, se tu usi nozioni probabilistiche, devi spiegarmi cosa intendi per probabilità.
A.-È proprio qui che ti volevo. Se definisci quale delle due stringhe è casuale in un certo senso definisci cos’è il caso ovvero il fondamento della nozione di probabilità.
A.-Prendiamo nuovamente questa moneta. Tu dici che la probabilità che esca testa o croce è esattamente 1/2. Questo perché 1/2 è l’inverso del numero degli eventi possibili purché questi eventi siano equiprobabili.
A.-Proprio così. Quindi dobbiamo avere un criterio per sapere se le uscite di testa o croce di questa moneta sono equi-probabili. Che cosa diresti se, lanciando questa moneta, ottenessi proprio la stringa S1?
A.-Dunque, per sapere se la mia moneta è un oggetto i cui lanci si comportano in maniera casuale, devo sapere che cosa è una stringa casuale.
A.-Hai ragione ma solo in parte. Infatti la stringa S1 ha una qualche probabilità di essere prodotta a caso solo perché è molto corta. Basta che tu la prenda un po’ più lunga e la probabilità diventerà praticamente 0. Per esempio, producendo una stringa al secondo, per ottenere una data stringa di 60 caratteri, non basta l’età dell’universo.
A.-Ma lo sai che sei più pedante di un matematico...
A.-Non essere sciocco. So rispondere a tutte le tue domande perché sono un personaggio inventato dall’Autore proprio con questo scopo. Per evitare il tuo problema, basta prendere stringhe casuali infinite e sviluppare il calcolo delle probabilità come ha fatto Von Mises più di 50 anni fa.
A.-No, perché Von Mises ha basato la nozione di probabilità su quella di successione casuale ma non è riuscito a dare una buona nozione di stringa casuale. Con questa teoria, invece, si può definire che cos’è una successione casuale. Basta che ogni segmento iniziale della successione sia una stringa casuale...
A.-Bene. Allora ragioniamo più alla buona. Se ti mostro le stringhe S1 e S2 e ti dico che una di esse è stata prodotta a caso mi dici che questa stringa è la S2 ma non sai il perché.
A.-Anche questo non è vero. Tu sai che un computer qualsiasi, anche con un programmino molto semplice, riesce a produrre stringhe casuali che resistono alla maggior parte dei test statistici. Ma queste stringhe non sono casuali perché sono prodotte da un programma deterministico. Infatti, vengono chiamate stringhe (o successioni) pseudo-casuali.
A.-Certo ma, per fare una distinzione appropriata tra stringhe casuali e pseudocasuali, devi avere già definito che cosa intendi per stringhe casuali. Altrimenti come fai a smascherare le pseudocasuali?
A.-Certamente: perché la S2 è casuale?
A.-A questo punto della nostra discussione, abbiamo appurato che ricorrere a nozioni probabilistiche per rispondere alla domanda iniziale non aiuta affatto perché, per dare una definizione non assiomatica di probabilità, devi già sapere che cos’è una stringa casuale per distinguerla da una pseudocasuale. Quindi devi definire la casualità in maniera intrinseca. Se riesci a fare ciò, non solo sai che cos’è una stringa casuale ma dai un fondamento accettabile al calcolo delle probabilità.
2.4. Quantità di informazione
A.-E quale?
A.-... e magari frutto del demonio, una prova dell’esistenza di Satana. Non essere ridicolo. Lo so che sei bravo in Filosofa, ma noi vogliamo fare un discorso terra terra e non è il caso di scomodare Dio. Vogliamo sapere solo perché la S2 è causale e la risposta, anche se è concettualmente profonda, deve essere formalmente semplice.
A.-Supponi che voglia comunicare la mia stringa ad un amico che vive... sulla luna e che le trasmissioni tra qui e la luna costino molto care e pertanto mi convenga rendere il mio messaggio il più corto possibile per risparmiare. Se voglio trasmettere la stringa S1, basta che trasmetta il messaggio 0001 che mi “prende” 4 bit, ed il messaggio di ripeterlo 10 volte, che mi prende altri 4 bit (in quanto 10, in numerazione binaria, si scrive “1010”). Dunque, posso trasmettere la mia stringa con 8 bit di informazione. Per trasmettere invece la stringa S2, non posso fare altro che trasmettere ogni simbolo alla volta ed impiegare 20 bit.
A.-D’accordo, ma se parliamo di stringhe lunghe, l’informazione per trasmettere tali regole è irrilevante.
A.-Più o meno.
A.-Ma bisogna ammettere che il tuo interlocutore sulla luna non sappia nulla.
A.-D’accordo, bisogna ammettere che sappia molto poco...
A.-Hai ragione. Adesso ti spiego tutto con ordine.
Teoria algoritmica dell'informazione 3.1. Come si misura la quantità di informazione?
A.-Hai presente che cos’è una macchina di Turing universale?
A.-È vero. In realtà, molte volte questi concetti non sono insegnati neppure all’Università (e mostra all’amico un disegno di una macchina di Turing e una tabella che ne illustra il funzionamento).
A.-Ma no! È solo un disegno schematico. Il disegno non ha importanza; nessuno ha mai costruito veramente una macchina di Turing. Se vuoi capire, devi guardare solo questa tabella qui.
A.-Comunque non ha importanza perché, al posto di una macchina di Turing universale, si può sostituire il tuo computer con un semplice linguaggio di programmazione.
A.-Il Basic o il Pascal fa lo stesso. L’unica astrazione che devi usare consiste nel fatto di supporre che il tuo computer abbia memoria infinita e che tu abbia la pazienza di aspettare che il programma abbia completato il suo ciclo (ammesso che si fermi).
A.-Non prendermi troppo alla lettera. Dicendo che un computer ha memoria infinita, voglio semplicemente dire che ha memoria sufficiente per farci girare un qualunque programma. Siccome non si può sapere a priori la memoria necessaria, si deve supporre che gli si possa aggiungere un po’ di memoria tutte le volte ciò si renda necessario.
A.-Hai capito benissimo. Una macchina di Turing si dice universale se può “simulare” ogni altra macchina di Turing. I computer che usiamo sono macchine di Turing universali. Puoi mettergli dentro il linguaggio che ti pare: Pascal, Basic, Lisp. E ciascuno di questi linguaggi può simulare un qualsiasi altro linguaggio.
A.-Allora, supponiamo che tu ed il tuo amico sulla luna abbiate due computer con lo stesso linguaggio di programmazione. Se vuoi fare in modo che sul display del tuo amico compaia la stringa S1, basta che tu spedisca il se-guente messaggio: “for n= 1 to 10, print “0001, next”. Questo messaggio è più corto del messaggio “print “0001000100010001000100010001000100010001””. A questo punto, si può definire la quantità di informazione contenuta in una qualunque stringa come la lunghezza del più corto programma che produce quella stringa. Una volta fissata una macchina di Turing universale Uo, per dirlo in parole povere, una volta fissato il linguaggio di programmazione, la quantità di informazione contenuta in una stringa S risulta essere un numero intero ben definito. Esso sarà denotato con il simbolo IU(x). In simboli, possiamo scrivere:
dove |p| denota la lunghezza del programma p (cioè il numero di 0 e di 1 che lo compongono) e U(p) denota la stringa prodotta dal tuo computer quando esegui il programma p.
A.-Questo è vero; ma questa dipendenza non è troppo grave. Infatti, se V è un altro linguaggio di programmazione, risulta che:
A.-Possiamo riepilogare tutti i passaggi: una stringa si dice casuale se non ha regole nascoste che la possano rendere più corta. Grazie alla nozione di “macchina di Turing universale” queste nozioni possono essere perfettamente formalizzate (a meno di costanti che non sono rilevanti dal punto di vista generale). Si può definire formalmente la quantità di informazione (chiamata anche complessità nel senso di Kolmogorov) contenuta in una stringa. A questo punto, una stringa può essere definita casuale se il suo contenuto di informazione I(x) è più o meno uguale alla lunghezza |x| della stringa stessa.
A.-Certamente, bisogna dare una valutazione quantitativa. Per motivi tecnici si è deciso di definire x casuale se:
Per esempio, se una stringa con un milione di caratteri non è casuale, può essere prodotta da una stringa un po’ più corta, ovvero da una stringa di soli:
caratteri.
3.2. Quante sono le stringhe casuali?
A.-Non sono molte, ma moltissime. Calcoliamo ad esempio quante sono le stringhe casuali di lunghezza N. In totale ci sono 2N stringhe di lunghezza N. Quelle che non sono casuali possono essere prodotte da stringhe appena un po’ più corte ovvero da stringhe di lunghezza N – log2N. Ma le stringhe di questa lunghezza sono al più:
e quindi le stringhe casuali sono almeno:
Dunque, tra le stringhe di un milione di caratteri, solo un milionesimo di loro possono essere non casuali. Il 99,9999% sono certamente casuali.
3.3. Numeri casuali
A.-Quindi la stragrande maggioranza dei numeri sono casuali.
A.-Poiché le stringhe possono essere poste in corrispondenza biunivoca con i numeri naturali secondo la seguente tabella (ordine lessicografico):
ne segue che ogni numero naturale può essere intrinsecamente casuale. Un numero n si dice casuale se:
A.-In base alla tabella, parlare di numeri naturali o di stringhe è la stessa cosa...
A.-... e quindi possiamo parlare di numeri casuali. Un numero n, in base alla tabella scritta sopra, può sempre essere rappresentato con log2(n+2) simboli. Ma può anche avere delle regole nascoste; per esempio, il numero 6.915.878.970 è il prodotto dei primi 10 numeri primi. Usando queste regole nascoste si può scrivere un programma che produce il numero n sul display del tuo computer. La lunghezza del più corto di questi programmi si denota con I(n) ed è il contenuto di informazione di n. Quindi non solo ti ho spiegato cos’è una stringa casuale ma anche che cosa è un numero casuale. Naturalmente, con questa definizione, i numeri piccoli sono tutti casuali...
A.-Non ho detto che quasi tutti i numeri sono equiprobabili; la probabilità è un’altra cosa...
3.4. Probabilità a priori di un numero
A.-Cosa mi diresti se affermassi che la probabilità a priori di un numero n non è altro che P(n) = 2–I(n)?
A.-Certo che ce li ho. Altrimenti, non avrei tirato in “ballo” questa questione. Mi dici che sei ancora affezionato al vecchio buon “lancio della moneta”. Bene: supponiamo di avere la tua moneta perfetta, lanciamola e vediamo qual è la probabilità che mi dia un certo numero.
A.-Non correre. Non voglio fare trenta lanci, voglio fare infiniti lanci. O meglio voglio fare N lanci e tenere conto di tutte le possibilità che esistono, qualunque sia il numero N.
A.-Guarda che la somma delle probabilità di ciascun evento indipendente deve essere uguale ad 1 e tu con soli sei numeri hai già raggiunto il numero 2:
P(0)+P(1)+P(2)+P(3)+P(4)+P(5)=1/2+1/2+1/4+1/4+1/4+ 1/4 = 2.
A.-La tua idea è buona, se vuoi definire la probabilità a priori di una quantità finita di numeri ma, se vuoi considerare tutti i numeri, il tuo fattore di normalizzazione diventa:
A.-Quasi nel modo che hai detto tu. Lanci la tua moneta e la successione di “0” ed “1” che ti viene sarà considerata un programma e messa in una macchina di Turing universale. Quindi aspetti il risultato. Questa volta la somma delle probabilità di ciascun numero ti verrà minore (o al più uguale) a uno, almeno se usi un piccolo accorgimento, ovvero che nessun programma sia uguale alla parte iniziale di un altro programma. Questo capita molto spesso nei programmi reali. Basta che un programma “dichiari” in anticipo la sua lunghezza. In questo caso la probabilità a priori di un numero è definita da:
ovvero la probabilità a priori di un numero è uguale alla probabilità che questo numero venga prodotto da un programma scritto lanciando in aria la tua moneta “perfetta”.
A.-Cerco di spiegartela: la probabilità che la tua moneta produca il programma p è data da 2–|p|. Quindi, se vuoi definire la probabilità che il tuo computer produca il numero n devi sommare le probabilità di tutti i programmi p che producono n ovvero tutti i programmi tali che U(p) = n.
A.-Non c’è niente di male: dato che esiste questa possibilità, se poniamo:
risulta Ω < 1. Ω è proprio la probabilità che un programma casuale si fermi. Il numero Ω si chiama numero di Chaitin e ha importanti proprietà aritmetiche legate a certe equazioni diofantee... ma non divaghiamo troppo...
A.-Torniamo alla nostra formula. Si può dimostrare che:
A.-Non prendermi in giro.
A.-È facile ottenere un numero o una stringa casuale, ma è difficile dimostrare che essi sono casuali. In un certo senso, si può soltanto dimostrare che una stringa non è casuale.
3.5. Il paradosso di Berry ed il teorema di Chaitin
A.-Intuitivamente è molto semplice: una stringa non è casuale se ha una regola nascosta. Se trovi tale regola, allora non è casuale. Se invece non trovi nulla, non sai se la tua stringa è casuale oppure se devi cercare ancora... e ancora... e ancora… e non sai mai quando fermarti.
A.-Ora sei tu che fai uso di brutti neologismi: “zippatore” fa più schifo della parola “stringa”.
A.-I tuoi zippatori funzionano solo perché i file che si usano sono ben lontani dall’essere casuali.
A.-Me lo dice il teorema di Chaitin. È un fatto della vita che la perfezione non esiste e qualche volta questo fatto si può dimostrare. Così non ci saranno più illusi come te che cercano la “pietra fifilosofale”.
A.-Non è altro che la versione informatica del paradosso di Berry.
A.-Parla di numeri e della loro definibilità mediante “parole”. Per esempio le proposizioni:
il più grande numero primo minore di cento il più piccolo numero perfetto il numero ottenuto moltiplicando i primi dieci numeri primi tra di loro sono proposizioni che definiscono rispettivamente i numeri 97, 6 e 6.915.878.970. Adesso considera la seguente proposizione:
@ Il minimo numero intero che, per essere definito, richieda più simboli di quanti ce ne sono in questa proposizione.
A.-Ma ne sei proprio sicuro?
A.-E sei anche sicuro che i numeri descrivibili “a parole” formino un insieme?
A.-Allora supponiamo che tale numero esista e chiamiamolo β: il numero di Berry. Poiché la proposizione “@” contiene 115 simboli (contando anche gli spazi vuoti), ciò vuol dire che per definire β ci vogliono almeno 116 simboli.
A.-Ma dimentichi una cosa: la proposizione “@” contiene 115 simboli e definisce il numero β.
A.-Cosa hai detto?
A.-Non è proprio il caso che ti stupisca tanto. I paradossi e le antinomie, in Logica come in Matematica, esistono fin da quando è stato inventato il ragionamento astratto cioè dai tempi dell’antica Grecia. In genere, nascono dall”’autoreferenza” cioè dal disporre di un linguaggio che può parlare di se stesso.
A.-Più o meno. Pensa, per esempio, al paradosso di Epimenide: se uno dice “io mento”, se mente veramente, dice la verità; ma, se dice la verità, allora mente. Con l’autoreferenza si possono trovare tutte le antinomie che vuoi.
A.-Ti sbagli, perché antinomie e paradossi, opportunamente interpretati, ti dimostrano che certe cose non si possono fare. Stabiliscono le colonne d’Ercole che separano il possibile dall’impossibile. Come, ad esempio, il paradosso di Berry. Tradotto nel mondo dei computer, diviene un teorema: il teorema di Chaitin, che stabilisce che con un programma P contenente una quantità di informazione I(P) = k non si può comprimere (in modo ottimale) una stringa avente un’informazione maggiore di k bit.
@@ il programma che è capace di provare che una stringa ha complessità algoritmica maggiore del numero di bit contenuti in questo programma.
Se il programma P esistesse, usandolo come subroutine, si potrebbe facilmente costruire il programma @@ che ha una quantità di informazione poco superiore a quella di P, diciamo k + k1 ed opera nel seguente modo:
In altre parole, il programma @@ ha prodotto una stringa x che ha informazione algoritmica maggiore di k + k1 ovvero U(@@) = x con I(x) > k + k1. Ma, dalla definizione di informazione, si ha:
Un pò di Filosofia 4.1. La versione informatica del teorema di Gödel
A.-Anche così, non sarebbe poco...
A.-Sì, la teoria ha molto a che vedere con il teorema di “incompletezza” di Gödel. Chaitin stesso ha dato molte dimostrazioni “informatiche” di questo teorema. Ti voglio raccontare in modo un po’ intuitivo di cosa si tratta. Torniamo all’Aritmetica, alla cabalistica come dici tu. Prendiamo un numero m e vediamo se ha regole nascoste ovvero se, pensato come stringa, è comprimibile. Questo fatto non può essere dimostrato con un programma p che ha un contenuto di informazione minore di I(m).
A.-Certo. Ma ora seguimi un po’ in questo ragionamento. Se tu scegli un numero finito di assiomi e formalizzi tutte le regole di inferenza di una teoria matematica (per esempio l’Aritmetica), otterrai un “programma” che ha un contenuto di informazione magari grande, ma finito.
A.-Certo. Un programma, chiamiamolo L, al quale, come input, dai un enunciato e, come output, aspetti una risposta: questo enunciato è vero (cioè è un teorema) oppure questo enunciato è falso. Basta che formalizzi bene le regole di inferenza e il tuo programma può produrre tutti i teoremi e verificare se sono uguali all’enunciato dato oppure sono uguali alla sua negazione. A questo punto il programma ti dà la risposta e si ferma. Il teorema di Gödel ti dice che un tale programma non può esistere, ma questo fatto te lo dice anche il teorema di Chaitin.
A.-Bravo, le cose stanno proprio così.
A.-Non ti gasare troppo. In realtà, abbiamo saltato tutti i dettagli tecnici. Comunque, per me, c’è una cosa ancora più sorprendente: preso un qualunque numero m > I(L), nonostante che quasi certamente sia casuale, sappiamo con assoluta certezza che non lo possiamo dimostrare. In altre parole, sono più le cose che non sappiamo di quelle che sappiamo.
A.-Già, ma la novità consiste nel fatto che questo vale per semplici proprietà aritmetiche. Se, con un computer potentissimo e con un programma p con I(p) > m, riuscissimo a provare che m è casuale, questo fatto andrebbe assunto come assioma indipendente.
A.-Ma non capisci: se questo è vero, viene distrutto il vecchio pregiudizio che la Matematica sia un sistema assiomatico deduttivo. In realtà, è una scienza empirica.
A.-La maggior parte delle verità verificate da un semplice modello come l’insieme dei numeri naturali, non possono essere dedotte da un sistema finito di assiomi, anche se potrebbero essere verificate con altri mezzi; proprio come capita nelle scienze empiriche. Una teoria, qualunque essa sia, non ti permette di prevedere tutto. Ci sono sempre fatti che le sfuggono e che richiedono che la teoria venga ampliata. In Aritmetica, quello che è dato a priori è l’insieme dei numeri naturali ma le verità che li riguardano non possono essere dedotte da un insieme finito di assiomi e di regole di inferenza. E quindi l’Aritmetica è una scienza sperimentale.
A.-Un po’ sì e un po’ no. In realtà, Chaitin ha proposto di introdurre la nozione di incertezza in Matematica ed accettare enunciati del tipo: “il teorema tal dei tali ha una probabilità a priori del 99% di essere vero”.
4.2. L’epistemologia di Salomonoff
A.-No! In realtà, quando ho detto questo, stavo pensando all’epistemologia di Salomonoff.
A.-Insieme a Kolmogorov e a Chaitin, è il padre di questa teoria. Anzi è il primo ad averne scoperto i punti essenziali. Ma fino a quando Kolmogorov non li ha riscoperti, nessuno ci aveva fatto caso. Comunque lui è arrivato a questa teoria attraverso altre motivazioni. Voleva trovare un criterio per sapere – almeno virtualmente – quale, tra due teorie scientifiche, fosse la migliore. Salomonoff ha pensato di rappresentare le osservazioni di uno scienziato mediante una successione di cifre binarie.
A.-Alla teoria spetta il compito di “spiegare” le osservazioni e di predirne delle nuove. Quindi una teoria scientifica può essere considerata come un programma che permette ad un computer di riprodurre le osservazioni. Se tra due teorie si deve scegliere la migliore, quale sceglieresti tu?
A.-Certo che è la vecchia teoria del rasoio di Occam, ma formulata matematicamente. E questo fatto la fa uscire dalla Filosofa delle opinioni per farla approdare ad una Epistemologia adatta alla scienza dei nostri giorni.
A.-Non so cosa pensino i popperiani, ma ti posso dire quello che penso io. A me pare che il criterio di scientificità proposto da Popper sia estremamente riduttivo. Per esempio, niente della Matematica sarebbe una teoria scientifica o, forse, lo sarebbe la Geometria euclidea in seguito ad accurate misurazioni relative agli enunciati dei suoi teoremi. E non solo la Matematica sarebbe esclusa dal mondo della scienza, ma anche molte teorie quali la teoria dell’evoluzione naturale, la teoria del big-bang, la teoria della deriva dei continenti, l’Astronomia,...
A.-Vorresti dire che Kepler è stato il più grande zippatore della Nuova Scienza?
A.-Vuoi dire qual è il significato epistemologico del teorema di Chaitin? In fondo ci dice quello che il buon senso ci ha sempre detto: non si può sperare di avere un algoritmo che ci permette di trovare in ogni occasione la teoria ottimale. La scoperta di una buona teoria è frutto di lavoro, intelligenza, intuizione e molta fortuna.
4.3. La tesi di Church
A.-Questo ovviamente non lo sa nessuno. Ma possiamo provare a formulare meglio il problema mediante la tesi di Church.
A.-Church è un signore che è considerato il maggior logico di questo secolo dopo Gödel. Mentre Gödel ha dimostrato che esistono cose vere che non possono essere dimostrate, Church ha provato che non esiste alcun metodo per sapere se una cosa è dimostrabile.
A.-Considera un sistema formale ovvero un linguaggio, degli assiomi e delle regole di inferenza. Il tutto deve essere perfettamente formalizzato: questo in pratica vuol dire che tutto il lavoro potrebbe essere fatto da un computer. Inoltre il nostro sistema formale deve “contenere” una teoria abbastanza ricca: diciamo l’Aritmetica. Dandogli tempo infinito, questo computer dovrebbe essere capace di stampare tutti i teoremi.
A.-Bene! Gödel ti dice che certe proposizioni non saranno mai stampate. Né loro né le loro negazioni. Dunque, aggiungendoci un po’ di fantasia, si può dire che certe cose non sono né vere né false. Questo fatto si esprime dicendo che il sistema è incompleto.
A.-Dice che non esiste una procedura di decisione, ovvero, per sapere se una cosa è dimostrabile o no, non ti resta altro che aspettare che il computer stampi quella proposizione o la sua negazione. Fino alla fine del tempo. Non c’è alcun metodo generale che ti permetta di sapere a priori quali sono i teoremi dimostrabili. L’unico mezzo a disposizione è quello di provare a dimostrarli, ma se non ci riesci, non puoi dedurre nemmeno che non sei abbastanza bravo.
A.-In realtà, sembra proprio che questo ampliamento non sia possibile. Turing, usando la sua macchina ideale, con metodi completamente diversi è giunto proprio alla stessa conclusione. E questo fatto ha portato Church a suggerire che qualunque effettiva computazione (o dimostrazione) operata da uomini e macchine poteva essere duplicata dall’uomo ideale o dalla macchina ideale e questa è la famosa tesi di Church. È una affermazione empirica, ma l’evidenza a suo favore è schiacciante. Poiché ogni operazione fatta da una macchina ideale o da un uomo ideale può essere fatta da una macchina di Turing universale, la tesi di Church-Turing può essere riformulata così: “Tutto quello che può essere calcolato, può essere calcolato da una macchina di Turing” o, se ti fa più piacere, pensando alla Matematica: “Tutto quello che può essere dimostrato, può essere dimostrato da una macchina di Turing” ovvero, pensando alle scienze empiriche e all’epistemologia di Occam-Salomonoff: “Tutto quello che può essere zippato, può essere zippato da una macchina di Turing”. Ogni computer, anche il più potente, non può fare niente di più di ciò che può fare una macchina di Turing universale. Ovvero, qualunque algoritmo può essere simulato da qualunque semplice computer. Basta supporre che abbia memoria infinita e che si abbia la pazienza di aspettare.
A.-Adesso non esagerare, tu non stai formulando la tesi di Church-Turing, ma la tesi di Church-Turing-Signor B. che recita così: “Tutto quello che può essere calcolato dall’intero universo, può essere calcolato da una macchina di Turing” e francamente mi sembra che sia un po’ troppo. In fondo l’universo è piuttosto grande. Ci sono più cose in cielo e terra di quanto la tua filosofia possa sognare. Nel mondo fisico ci possono essere fenomeni che sfuggono ad una descrizione algoritmica. Dando per buona la tesi di Church, ci si può porre la seguente domanda: esiste qualche fenomeno fisico che calcola qualcosa di non-calcolabile?
A.-Proprio così. Il problema, riformulato opportunamente, diventa questo: il cervello umano, con lavoro, intelligenza, intuizione e molta fortuna, può calcolare qualcosa che è (algoritmicamente) non-calcolabile o dimostrare qualcosa che è (algoritmicamente) non-dimostrabile o comprimere una teoria che è (algoritmicamente) non-comprimibile?
A.-Hai ragione. Abbiamo chiacchierato anche troppo. Andiamo al bar della Facoltà a farci la solita partita a Magic con il resto della compagnia. |