Guarino Guarini architetto e matematico
Guarino Guarini architetto e matematico
Un pò di storia

Guarino Guarini nasce nel 1624 a Modena.
In giovane età entra a far parte dell’ordine dei Teatini che lo inviano a Roma per il noviziato. Trascorre nella città papale otto anni, dal 1639 al 1647, durante i quali ha modo di conoscere e studiare l’architettura barocca, soprattutto nell’interpretazione del genio borrominiano. Dei grandi maestri barocchi, il giovane Guarino eredita il rigore costruttivo, la fantasia delle infinite articolazioni strutturali e il gusto del colore nella scelta dei materiali. Conclusi gli studi, torna nella città natale per essere ordinato sacerdote e per iniziare la carriera accademica con l’insegnamento della matematica e della fisica. In questo periodo approfondisce lo studio degli aspetti teorici dell’architettura.
Nel biennio 1660-1662, durante un soggiorno a Messina, progetta e realizza la chiesa della Santissima Annunziata, la Casa dei Teatini, la chiesa di San Filippo e la chiesa dei Padri Somaschi.
Quest’ultima opera ha un’importanza particolare in quanto compare per la prima volta il tipo della cupola aperta ad archi intrecciati che diventerà uno dei motivi predominanti dell’architettura del Guarini.
Poco tempo dopo il ritorno a Modena viene inviato a Parigi per occuparsi della costruzione della chiesa di Sainte-Anne-la Royale.
Nel 1666 viene chiamato a Torino dove rimane fino al 1681 come ingegnere e matematico di Carlo Emanuele di Savoia.
L’incarico affidatogli permette all’architetto di esprimere nel modo più compiuto il proprio genio sia quando ha la possibilità di progettare edifici ex novo sia quando è costretto ha costruire su preesistenze.
Pressoché tutti i grandi cantieri piemontesi del periodo registrano l’intervento del Guarini, soprattutto nel cuneese e in Torino dove realizza, oltre alla Cappella della Santa Sindone e altri edifici quali Palazzo Carignano, che rappresenta l'apice dello sviluppo del palazzo italiano del XVII secolo, la chiesa di San Filippo e la Chiesa teatina di San Lorenzo, in cui Guarini supera definitivamente la concezione della cupola classica trasformandola in una leggerissima struttura trasparente evocativa dell'infinito celeste.
Durante il lungo soggiorno torinese compie alcuni viaggi in Europa, a Praga e a Lisbona in particolare, in occasione di richieste di interventi.
Gli anni trascorsi presso il ducato di Savoia consentono all’architetto di occuparsi anche di argomenti teorici riguardanti la matematica e le discipline da essa derivate: geometria, astronomia e architettura.
Muore a Milano nel 1683.
La cappella della Sindone a Torino
Il nome di padre Guarino Guarini si colloca ai vertici dell’architettura religiosa e civile del Seicento. Pertanto, sebbene gli studi condotti nel secolo scorso siano limitati, si sono chiariti molti concetti sulla sua creazione artistica 1. Rimane tuttavia ancora insoluta la questione fra società civile, scienza e arte, perfettamente rappresentata dalla Cappella della Sindone a Torino. Guarini intuì, nel corso della realizzazione di quello straordinario monumento e quindi tramite l’architettura, il nesso profondo fra la teologia, “regina scientiarum” incarnata dal vescovo di Torino, la funzione votiva della Cappella, custode tra l’altro dei sepolcri dei Savoja (residenti nell’attiguo Palazzo Reale) e il sapere astratto delle discipline matematico-fisiche.
Nella Cappella lo spazio architettonico esprime l’astratto attraverso elementi tangibili, confrontabili ad occhio, come accade nella complessa struttura musicale di J.S. Bach che da, limitati rapporti fra note, costruisce l’arte della fuga2.
Nel percorso verso l’Estetica, la moderna Filosofia dell’arte non ancora nata3, Guarini progettò un nuovo esempio di Bellezza dimostrabile attraverso precise misurazioni, la proporzionalità delle parti, la coesione degli spazi, secondo intervalli numerici del tre, del sei, del nove. Già i Greci nel Partenone (448 a.C.) o il Rinascimento a Urbino, nella metà del XV secolo, con Piero della Francesca o Francesco di Giorgio Martini, operanti per Federico da Montefeltro, sperimentarono la complessità visiva della sezione aurea4, ad esempio nel Palazzo Ducale, con rapporti sempre più articolati fra segmento e lato del quadrato o fra base, portale, finestre, altezza.
Guarino Guarini sfidò i limiti della ragione umana, portando alle estreme conseguenze l’idea di uno spazio preesistente nella mente, perciò intuitivo per volere di Dio, parcellizzato in infinitesime suddivisioni della superficie. La cupola della Sindone ha una storia tormentata, stupefacente, pessimistica al pari della filosofia di S. Agostino: si insinua il dubbio sull’esistenza di Dio e sul senso della vita umana per aprire poi la strada al sapere.
Il lenzuolo della Sindone fu oggetto di devozione storica fin dal 1452, quando Torino divenne capitale del ducato di Savoja, ma solo con Emanuele Filiberto si decise di innalzare una cappella, in un luogo angusto, dietro l’abside del Duomo cinquecentesco, per ricordare la vittoria riportata dai Cristiani a Lepanto (1571). L’edificio era deputato ad accogliere la reliquia di Cristo, miracolosamente sopravvissuta al Medioevo, e il mausoleo del principe regnante.
Si susseguirono da allora ben tre progetti: il primo fu commissionato da Carlo Emanuele I a Carlo di Castellamonte, il secondo fu affidato ad Amedeo di Castellamonte da Carlo Emanuele II (1655) che, successivamente, per motivi non chiariti e a costruzione già iniziata, chiamò Guarino Guarini (1667)5. Solo nel 1694, ben oltre la morte dell’autore, la cupola fu completata.
Il tema proposto richiedeva le più elevate cognizioni del sapere umano; non si poteva infatti dimostrare logicamente la morte di Dio ma solo il fatto che il Signore aveva abdicato, in via transitoria, ad una collocazione assoluta, extratemporale, come voleva la tradizione tomistica, per conoscere la morte fisica, ingiustificata, percorsa dalla sofferenza e dal disonore della croce. La parte terrena della cappella meditava in modo desolante sull’impossibilità di rifiutare una condanna ingiusta e la reliquia mostrava un Uomo sacrificato. Non si potevano certo utilizzare soluzioni scontate, coreografiche o teatrali secondo le posizioni retoriche di Bernini che nel Colonnato di S. Pietro aveva saccheggiato le geniali teorie proposte da Caramuel facendole sue6.
L’accesso alla Cappella della Sindone fu elaborato a partire da elementi instabili, contrastanti fra loro, capaci di soddisfare un pubblico elevato e poco propenso alla devozione popolare. I tre ingressi regolari, ad angoli di 120°, lasciavano il ruolo privilegiato ai Principi, che entravano direttamente dall’ala nuova del Palazzo, e, nel contempo indicavano ai pellegrini che affollavano la chiesa un percorso a senso unico che non intralciasse le funzioni del Duomo7.
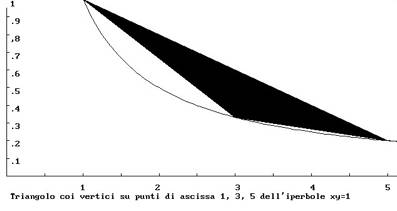
fig.1.a. Cappella della Sindone: pianta, angoli e rapporti numerici (da Passanti, 1963)
Si era costretti a ruotare intorno alla teca nei due sensi orario e antiorario (fig.1), secondo una concezione che privilegiava il tempo storico, il limite di una breve stagione dove ogni essere, anche elevato, perdeva la sua vita.
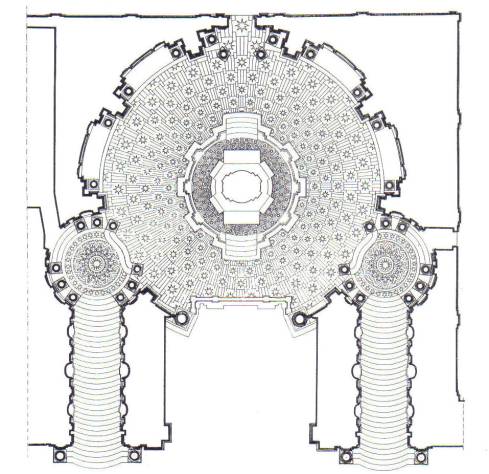
fig.1.b. Cappella della Sindone: scaloni, atrii, pavimento e sacello (da Passanti, 1963)
Il pessimismo del pavimento a marmo nero con decori chiari accentuava lo spietato avanzare dell’esistenza nonostante la stella a otto punte, ripetendosi con ossessione, inneggiasse alla cometa dei Magi8, all’Epifania e, ancora, alla vita eterna.
Al vano centrale si perviene con scaloni e atrii che consentono di celare a chi sale la vista della Cappella e a chi scende la distrazione dell’uscita9. L’uomo è in una morsa terrena da cui non riesce a sottrarsi con la sola volontà.
Non ci sono stucchi policromi, pitture, spunti evasivi o sensuali come perfino Francesco Borromini10, grande solitario, mostrava nel suo S.Ivo alla Sapienza. I gradini a Torino sono concavi o convessi, larghi, a segnalare la fatica di calpestarli, trattenendo o spingendo avanti il pubblico fino agli atrii. La balaustra aumenta l’angolo di visuale prospettica ma si schiaccia contro la parete, non è libera, impedendo al corrimano di confortare la salita.
I semipilastri (fig.2) comprimono le forze interne al muro con due lievi curvature quasi convesse, opposte all’andamento della scalinata. I soffitti scuri, opprimenti sono invece concavi, con valve di conchiglia troncoconiche, e sfociano nella copertura triangolare degli atrii circoscritta da una duplice circonferenza.

fig.2. Cappella della Sindone: scalone, rampa, nicchie ad incasso, atrii e coperture (da Passanti, 1963)
Inizia a demarcarsi l’idea di uno spazio mutante, imprevedibile, che conduce a Cartesio, filosofo di straordinaria portata per Guarini reduce da Parigi. Nelle “Regole per la direzione dell’intelletto”, che certo l’architetto non conobbe essendo state pubblicate postume nel 1701, Cartesio diceva che le discipline matematiche erano l’involucro contenente i primi rudimenti della ragione per trarre verità da qualsiasi oggetto11, anche artistico. La Filosofia è come un albero per Cartesio, con radici metafisiche e tronco di natura fisica; analogo è per Guarini il piano, ente neutro da cui uno scienziato-filosofo trae le condizioni visive per mettere a fuoco una catena di valori razionali. Padre Guarino, secondo lo storico Mario Passanti, sarebbe partito da uno stato creativo incosciente o forse meglio prelogico, precedente cioè il calcolo e le sue formulazioni12.

fig.3. Cappella della Sindone: basamento a triangolo con pilone, vela e imposta del tamburo (da Passanti, 1963)
Entrati da atrii a “gomito”, di scarsa ampiezza, ruotanti su un perno di colonne corinzie che lentamente si staccano dalla parete (fig.2, 3 e 4), si percepisce la circolarità della Cappella rivolta al cielo, all’armonia interiore, in una distanza remota.

fig.4. Cappella della Sindone: sezione della cupola (da Passanti, 1963)
Al sommo della cupola in forma di guglia quasi gotica vi è la Colomba dello Spirito Santo che domina sull’uomo nella caduta della morte e sulle urne dei Savoja su cui spiove la luce della fede in quanto difensori dal pericolo turco prossimo a Vienna (1683).
L’uomo da solo non può avvicinarsi alla volta celeste se non con le regole della Geometria e della Matematica: si impone dunque all’intelletto un metodo cartesiano.
Le verticali della cupola crescono con le regole della chiarezza e dell’evidenza13. Ogni linea si mette in mostra senza muri di supporto, violando le leggi statiche della Fisica galileiana; conta molto di più la disciplina geometrica applicata ai numeri come indicato dal reparto del tre (fig.3). Cartesio afferma che l’analisi riduce ogni problema complesso alle nozioni più semplici non scomponibili e cosa c’è di più semplice di un triangolo equilatero all’appoggio?
Così succede: l’ordine maggiore parte da tre immensi arconi su pilastri che precedono tutto lo svolgimento superiore e dai piloni nascono pennacchi concavi con nove croci annullanti la neutralità dello sfondo.
Le croci sono spunto di analisi e invitano ad aprirsi in verticale, ma la potente circonferenza della finestra14 si colloca quale intermedia fra pilastro e architrave superiore.
In sostanza si resta sospesi tra cielo e terra. Ecco allora la direzione della sintesi che Descartes riferisce all’ordine di passaggio dalla semplicità di un oggetto alla complessità.
Tutta quanta questa parte della Cappella induce al movimento orizzontale e verticale: è il moto precario di chi vive sulla terra e il concatenamento geometrico è maggiore proprio dove gli elementi tettonici si ostacolano, ossia in basso.
Il reparto del sei subentra a seguito di una circonferenza e si chiude con la circonferenza superiore ma nasce dal netto e violento taglio degli architravi susseguentisi l’uno nell’altro (fig.4). Sul cilindro si distaccano serliane con colonne sporgenti, non complanari all’arco che ruota in proprio; la vetrata è lontana, esterna alle superfici, mentre negli spazi di giuntura si aprono nicchie convesse con un aspetto manieristico degno di Palazzo Marino (fig.4-2).
L’aspetto è intermedio se confrontato con le soluzioni proposte in quota elevata per rendere il senso di inaccessibilità dal nostro mondo fatto di sfiducia e di costante pericolo nonostante la garanzia cristiana.
L’idea del cono convergente nel nostro occhio appare schiacciante, annulla la povera mente dell’uomo attratta dall’infinito. I poligoni si ripetono per sei volte con archi che mostrano tori, ora vicini ora lontani, senza toccarsi mai, in una concezione musicale simile alla fuga di Bach.
La ragione compie uno sforzo immane per arrivare a Dio. Gli archi formano sottili poligoni ad incastro, con catene tese al massimo. La luce si apre un varco da vetri impercettibili, in una situazione quasi islamica, continuamente cangiante nelle ore o nelle stagioni (fig.5).

fig.5. Cappella della Sindone: schema grafico della cupola (da Passanti, 1963, modificato)
La conclusione dell’itinerario ricorda le parole di Pascal: non basta lo spirito della geometria che distingue e rende incontestabili le proprietà delle figure e degli elementi. Non occorre solo lo spirito di finezza che è comune a tutti, parla al cuore, sorprende e vede con spontaneità16. La finezza è intuizione, la geometria intelligenza: bisogna perciò integrare entrambe. I raggi e la colomba dello Spirito Santo danno avvertimenti proprio sulla presenza di Dio laddove la ragione si è fermata. D’altro canto il metodo matematico prepara all’ineffabile e annuncia la coscienza che Dio esiste. Ecco quindi il cupolino remoto abbagliando farsi strada. Ogni elemento architettonico barocco viene eliminato per l’arditezza degli spazi, così come farà Alessandro Antonelli nel XIX secolo nella sua celebre Mole: siamo a un passo dalle congetture contemporanee sullo spazio.
Note bibliografiche
1. La bibliografia essenziale su G. Guarini comporta tre contributi importanti: M. Passanti, “Nel mondo magico di G.Guarini”, Torino, 1963; A.A.V.V., “G. Guarini e l’internazionalità del Barocco, atti del congresso internazionale”, Torino, 1970; H. Meek, “G.Guarini”, Milano, 1991, opera completa su tutte le fasi dell’autore.
2. Su J.S.Bach la monografia utile al nostro caso è in C.Wolff, “J.S.Bach, la scienza della musica”, Milano, 2003, dove si definisce Bach attraverso il necrologio di Friedrich Agricola come musicista dallo sviluppo intricato di un tema musicale serio (pp. 12-13).
3. L’Estetica nascerà in Inghilterra nel ‘700 come autonoma dal senso morale con Shaftesbury e Hutcheson (1694-1746).
4. Sulla sezione aurea si confronti il saggio di A. Marcolli a proposito della crescita organica e sezione aurea in “Teoria del campo”, Firenze, 2001.
5. Cfr. M. Passanti, op.cit. pag 165.
6. Sul Bernini le monografie più complete sono quelle di V. Mariani, “G.L.Bernini”, Napoli, 1974, e F.Borsi, “Bernini architetto”, Milano, 1980.
7. M. Passanti, op.cit., pag 189.
8. O. Beigbeder, “Lessico dei simboli medievali”, Milano, 1997, pp.69 e 229, esamina l’origine lontana della stella cometa in rapporto ai rilievi.
9. M. Passanti, op.cit., pag 189.
10. Su Borromini si veda: P.Portoghesi, “Borromini nella cultura europea”, Roma, 1982. Per il rapporto Guarini-Borromini si veda A. Griseri, “Le metamorfosi del Barocco”, Torino, 1967.
11. Riportato in E. Balducci, “Storia del pensiero umano”, Milano, 1986, II, pag. 109.
12. M.Passanti, op.cit., pag.189.
13. In R. Cartesio, “Il discorso sul metodo” a cura di G. De Ruggiero, Firenze, 1938.
14. Si parla di occhi o false finestre ma anche di vere finestre a zone alterne.
15. Analisi magistrale del percorso in R.Wittkower, “Arte e architettura in Italia”, Torino, 1972.
16. Non a caso Pascal inserisce la fisica, la musica e l’architettura nelle discipline che dipendono da esperienza e ragionamento, cfr. M. Dal Pra, “Profilo di storia della filosofia”, Firenze, 1971, II, pp. 115-116.
Il ruolo della matematica e della scienze nell'opera di Guarini
Analizzando con maggior dettaglio il rapporto fra Arte e Matematica, Guarini rappresenta indubbiamente una delle figure più interessanti di tutti i tempi. Legato alla tradizione ma profondamente attratto dalle scoperte scientifiche della sua epoca, è un intellettuale poliedrico: egli stesso si definisce teologo, filosofo, matematico oltre che architetto e pare che proprio la Matematica, al cui studio comincia ad avvicinarsi a Roma, dove si reca nel 1639 dopo essere entrato nell’ordine dei Teatini, lo abbia introdotto all’architettura.
La prima domanda che ci si pone è dunque se Guarini possa essere considerato a tutti gli effetti un matematico. Il suo contributo, paragonato con quello di altri personaggi italiani dell’epoca, quali Bonaventura Cavalieri (1598-1647) o Evangelista Torricelli (1608-1647), non appare determinante e questo è il motivo per cui il suo nome viene citato da pochi storici della matematica tra cui Chasles (1793-1880) in “Aperçu historique sur l’origine et le developpement des methodes en geometrie” (1837), in merito agli studi sulle sezioni coniche e sulla geometria descrittiva, e Gino Loria (1862-1954) che, in “Storia della geometria descrittiva” (1921), colloca i lavori di Guarini nelle fasi iniziali della costruzione di tale branca.
Per entrare in merito alla questione occorre far riferimento all’opera enciclopedica (la prima nel suo genere apparsa in Italia) “Euclides adauctus et methodicus mathematicaeque universalis” dedicata da Guarini a Carlo Emanuele II duca di Savoia, e pubblicata a Torino nel 1671. Scritta a scopo didattico, è una sorta di “summa” di oltre settecento pagine, composta da trentacinque trattati costituiti da una breve introduzione, commenti, definizioni, teoremi, problemi, costruzioni geometriche e da indicazioni esplicite e puntuali sulle fonti.
Circa metà dell’opera è dedicata ad argomenti puramente geometrici, tra cui un’analisi dei dodici libri di Euclide: è significativo osservare come Guarini, in un secolo in cui il ruolo dell’Algebra diventa sempre più rilevante (si pensi all’uso che ne fa Cartesio o addirittura al tentativo di Wallis di liberare l’Aritmetica e l’Algebra dalla rappresentazione geometrica), consideri la Geometria superiore rispetto agli altri rami della Matematica. Il resto dell’”Euclides” riguarda il calcolo dei logaritmi, sviluppato proprio all’inizio del Seicento da Briggs e Nepero, la Trigonometria ed il suo utilizzo nella risoluzione dei triangoli piani e sferici, l’astronomia e si chiude con una serie di tavole numeriche.
Dal punto di vista dei riferimenti architettonici, sono interessanti il XVIII trattato, che riguarda il problema della misura del cerchio e di curve particolari come la spirale, la quadratrice, l’ellisse, la conchiglia, la cicloide, riprese dai Greci e oggetto di analisi da parte di molti matematici e scienziati dell’epoca, il XXIV trattato, che riguarda le sezioni coniche, di fondamentale importanza sia per le loro applicazioni in campo astronomico sia per lo sviluppo della Geometria proiettiva di Desargues, e il XXXII trattato, che riguarda lo sviluppo su un piano di linee curve e di superfici tridimensionali e interpretato da alcuni critici come un’illustrazione teorica dei risultati ottenuti nella realizzazione delle volte. A proposito delle sezioni coniche, è curioso notare che nell’”Euclides”, con un richiamo piuttosto esplicito alla prima legge di Keplero, si sostiene l’utilità dell’ellisse per spiegare i moti dei pianeti: forse Guarini, pur difendendo il sistema geocentrico contro la teoria copernicana, comincia a nutrire qualche dubbio circa la sua sostenibilità.
Un altro trattato legato all’architettura è il XXVI, sul tema delle proiezioni, riprese qualche anno più tardi nei capitoli di ”Architettura Civile” dedicati all’ortografia elevata e all’ortografia gettata. Dalla sua introduzione, emerge l’attenzione dell’autore nei confronti delle applicazioni delle tecniche descritte: “Proiectionum usus amplissimus, tum horologijs, tum instrumentis mathematicis, v.g. astrolabio et quadrantibus: tum cosmographiae in planum ad circulos longitudinis, et latitudinis proiciendos, et tandem , et maxime architecturae ad proicienda corporum, singularumque planicierum delineamenta perutilis. Et hinc prospectivae, cum prius illud, quod iuxra diminutionem ocularis prospectus representatur in planum estendere oporteat, et ipsa quoque corpora, superficiesque in planum proicere”.
Sappiamo che, durante la sua permanenza a Parigi (dal 1662 al 1666) Guarini ha modo di apprendere le teorie di Desargues, Pascal, Cartesio e Fermat e di coltivare un interesse che lo accomuna alla maggior parte dei matematici del Seicento, cioè quello per l’infinito ed il calcolo infinitesimale (si pensi all’utilizzo dei metodi di interpolazione e allo studio di alcune serie da parte di Stevino, Keplero, Galileo, Cavalieri, Roberval, Torricelli, Wallis, Fermat). Perciò, proprio l’applicazione della Geometria proiettiva di Desargues costituisce tuttora motivo di dibattito tra i critici: alcuni affermano che questa rappresenti effettivamente la base teorica delle audaci costruzioni guariniane (in particolare le cupole) mentre altri, sottolineando la distinzione tra i concetti di proiezione e di geometria proiettiva, sostengono che le piante o le prospettive disegnate da Guarini non siano sufficienti per capire quanto egli veramente sia andato oltre la Geometria euclidea con la consapevolezza del significato più profondo della Geometria proiettiva, cioè del fatto che tutte le proprietà di una figura tridimensionale si possono dedurre da una sua opportuna rappresentazione1.
Lo stile dell’”Euclides” risulta piuttosto pesante, nonostante l’autore dichiari l’intento di semplificare dimostrazioni e ragionamenti. Ciò è più che comprensibile e giustificabile dal momento che la mancanza del calcolo letterale e di un linguaggio algebrico rende inevitabilmente complesse e poco leggibili persino le più banali relazioni fra grandezze geometriche elementari (si provi a leggere il trattato XXI sui logaritmi: l’esposizione di concetti relativamente semplici come l’uguaglianza tra il logaritmo del quadrato di un numero e il doppio del logaritmo del numero stesso richiede parecchie pagine).
Guarini scrive altre opere di carattere sia matematico che astronomico quali il manuale di gnomonica “Leges temporum et planetarum”, pubblicato a Torino nel 1678, e l’enciclopedia in due volumi “Coelestis mathematica”, pubblicata a Milano nel 1683 e dedicata alla misurazione del tempo, alla progettazione e costruzione di orologi solari e alle leggi che governano il movimento dei corpi celesti. Tuttavia, il testo più notevole è forse l’”Architettura civile”. Pubblicato postumo a Torino nel 1737 a cura dei confratelli teatini, è diviso in cinque trattati: sull’architettura in generale, sull’ichnografica (problemi di misurazioni, livellamenti, rappresentazioni planimetriche), sull’ortografia elevata (ordini architettonici e facciate), sull’ortografia gettata (proiezioni di cilindri, sfere e corpi ellittici su piani), sulla geodesia (metodi di scomposizione e trasformazione di figure e calcolo di aree). Nonostante il procedimento seguito nella presentazione degli argomenti di carattere geometrico non sia sempre rigoroso - ad esempio nel trattato sull’ortografia gettata vengono analizzati senza alcuna distinzione sia i casi in cui lo sviluppo di un solido è possibile in modo esatto (cono e cilindro) sia quelli in cui ciò è possibile solo ricorrendo ad approssimazioni (sfera e toro) – il lavoro di Guarini è senza ombra di dubbio apprezzabile e mostra inequivocabilmente tutta la sua passione per la matematica.
Riguardo all’uso del calcolo nella realizzazione delle opere architettoniche, in nessuno scritto compare traccia di calcoli statici o di considerazioni sugli sforzi e sulla resistenza dei materiali e l’applicazione della Matematica sembra limitata alla rappresentazione delle piante e degli edifici. D’altra parte, la scienza delle costruzioni è una disciplina recente sebbene qualcuno la faccia risalire a Galileo che nei “Dialoghi su due nuove scienze” (1638) affronta alcuni problemi sulla flessione delle travi.
L’arditezza degli edifici guariniani è dunque frutto dell’intuizione e dell’esperienza più che dell’applicazione concreta del calcolo ma la Geometria ha determinato lo sviluppo di una particolare forma mentis e, facendo riferimento ancora una volta agli scritti, si può cercare di capire in che modo e in che misura la concezione del mondo e dell’arte, il significato attribuito alle figure e l’iconografia usata ne siano il frutto.
Si è già accennato al fatto che, a partire dalla prima metà del 1600, si ha un’eccezionale produzione di testi di Geometria (ad esempio quelli pubblicati in Italia dagli intellettuali del circolo di Galileo, come Guidobaldo del Monte e Bonaventura Cavalieri, oppure in Francia dal gruppo dei cartesiani) e molti dei problemi affrontati derivano da necessità pratiche. In proposito, citiamo una frase di Desargues: “Devo confessare apertamente che non ho mai avuto gusto per lo studio e per la ricerca né in geometria né in fisica se non in quanto esse potevano servirmi come mezzi per arrivare a una qualche sorta di conoscenza delle cause prossime (…) per il bene e la comodità della vita (…) nella pratica di qualche arte (…) avendo osservato che buona parte delle arti si basa sulla geometria, come fra le altre il taglio delle pietre in architettura, l’arte delle meridiane e in particolare l’arte della prospettiva.” .
L’interesse per la Geometria emerge anche dai trattati di architettura e Guarini, seguendo questo filone, oltre a scrivere un’opera strettamente matematica come l’”Euclides”, inizia l’”Architettura civile” con una serie di principi di geometria, giustificando così la sua scelta: “l’Architettura, come facoltà che in ogni sua operazione adopera le misure, dipende dalla Geometria, e vuol sapere almeno i primi suoi elementi”. L’intenzione dell’autore, secondo Griseri4, è quella di verificare anche graficamente l’idea delle curve da utilizzare e al contempo porre a fondamento di ogni volume architettonico-figurativo una trattazione geometrica, alla ricerca di una genesi chiara e dimostrabile.
Il metodo di progettazione di Guarini, in un contesto barocco dove la pluralità dei punti di vista vuole stimolare una visione al contempo centripeta e multipla dello spazio architettonico, può essere interpretato alla luce delle nuove scoperte in campo astronomico e del nuovo ruolo assunto dalla Matematica. La forma dell’edificio, impostata su principi geometrici, aderisce ad un concetto generale di evoluzione che parte dalle componenti maggiori del progetto e dove i particolari della pianta e dei prospetti vengono sviluppati in un momento successivo, in fase di rifinitura, quasi come elementi complementari. Inoltre, grazie alla piena padronanza degli strumenti tecnici e forse grazie a conoscenze di Geometria superiore, lo schema generale viene spesso interpretato con piena libertà; Guarini stesso scrive6: “L’Architettura, sebbene dipendente dalla Matematica, nulla meno ella è un’arte adulatrice, che non vuole punto per la ragione disgustare il senso: onde sebbene molte regole sue seguano i suoi dettami, quando però si tratta che le sue dimostrazioni osservate siano per offendere la vista, le cangia, le lascia, ed infine contraddice alle medesime …”.
Se Bernini per i suoi edifici adotta misure di facile applicazione, l’architetto modenese stabilisce inizialmente solo le dimensioni degli spazi principali, determinando poi, con costruzioni geometriche, le dimensioni minori, molte delle quali, inevitabilmente incommensurabili.
Nella sua opera la natura dei rapporti spazio interno-massa esterna, luce-spazio, spazio-struttura generalmente non è di facile lettura e accanto alla complessità dello schema si ha una sovrapposizione delle forme architettoniche al fine di creare una continua tensione e di suggerire anche il modo per superarla.
Ogni cappella, parete o colonna risulta subordinata allo sviluppo di un’unica idea, perciò i particolari decorativi, le proporzioni e qualsiasi altro elemento possono essere modificati o addirittura eliminati per soddisfare alle esigenze spaziali concepite mediante un processo di elaborazione geometrica. Argan2 afferma che Guarini trasforma elementi decorativi in elementi funzionali e viceversa, allo scopo di raggiungere un risultato figurativo che accentui il rapporto tra la massa e lo spazio, tra i diversi elementi e tra gli elementi e la luce, simbolicamente intesa come generatrice di vita.
Poiché “nulla è nell’arte o nella scienza che non sia stato prima nella geometria”, la geometria diventa una sorta di Weltanschauung, forma simbolica, idea pura, matrice di tutte le scienze e le arti e per mettere in risalto la portata di questa “filosofia della geometria” o “geometria filosofica” si è proposto1 di definire il sistema intellettivo su cui si fonda l’opera guariniana con il termine geosofia. Nella geosofia convergono la Filosofia, l’Astronomia, la Fisica, la Teologia, la Trattatistica, l’Architettura, l’Ingegneria e persino la Poesia: la base è il numero e la Geometria rappresenta il più alto dei valori (in questo porre la geometria a fondamento del metodo filosofico si può riconoscere un influsso galileiano). Lo stesso trattato “Placita philosophica”, pubblicato nel 1666 a Parigi, ha una struttura geometrica. Diviso in sei parti, costituisce un tentativo di comprendere tutto il sapere umano, dalla logica alla fisica all’astronomia alla metafisica. In esso Guarini dichiara di voler esporre gli argomenti “physicis rationibus, experimentiis, mathematicisque figuris” e, in questo processo di razionalizzazione, arriva al punto di inserire il capitolo “De arte” nella parte sulla Fisica, sostenendo che tutte le arti dipendono dalla Matematica, dalla Filosofia o dalla Medicina, Scienze che trattano delle analogie tra le cose, delle loro proporzioni e dei loro rapporti naturali.
La Matematica interviene in ogni ambito: “Il modo di misurare le fabbriche” (1674) non è altro che un corso di matematica elementare, una versione pratica dell’”Euclides”; il “Trattato di fortificazione” (1676) basa persino l’analisi delle strategie di assedi e battaglie su principi matematici; la prefazione dell’”Euclides” fornisce una codificazione della matematica e dei numeri come simboli dell’arte divina. Le “mathematicae luces” pervadono il campo dell’architettura che spesso diventa il luogo in cui visualizzare teoremi geometrici e l’osmosi tra arte e scienza può essere colta confrontando le immagini degli edifici con le immagini riportate nei trattati.
Ad ogni numero è legata una figura geometrica: basti come esempio l’abbinamento del numero tre al triangolo equilatero così insistentemente utilizzato nella Cappella della Sindone per il suo significato matematico, estetico e soprattutto esoterico, in quanto simbolo della perfezione e della sapienza trinitaria. Ogni partizione della Cappella della Sindone, sia in pianta che in alzato, è basata sui numeri 3, 6, 12, 36: tre sono i vestiboli circolari inseriti nello spazio principale per un terzo della loro circonferenza, con le colonne sistemate a triadi e raccordate da archi a sesto ribassato che a loro volta disegnano un triangolo equilatero sul soffitto; tre sono gli archi impostati sulle coppie di lesene che fiancheggiano i vestiboli e tre i pennacchi che si inseriscono tra un arco e l’altro; sei sono i finestroni ad arco della zona mediana; sei sono gli anelli di altezze decrescenti in cui risulta divisa la cupola e che generano un "nido" composto da trentasei archi; dodici sono le punte della stella al culmine della cupola, come pure i contrafforti esterni; di un trentaseiesimo di circonferenza sono ruotati gli ovali del tamburo e della cuspide rispetto ai finestroni (fig.5, sopra, e 8).

fig.8. Cappella della Sindone: interno (da Passanti, 1963)
Il triangolo costituisce il poligono primo, l’indivisibile, l’atomo della geometria, la figura in cui ogni altro poligono è scomponibile.
Guarini, nei suoi edifici predilige figure regolari, dal triangolo equilatero all’esagono, all’ottagono, al cerchio, luogo di perfezione, simbolo di universalità divina (a conferma di ciò, si noti che l’ellisse viene impiegata prevalentemente in ambienti laterali o minori o in elementi decorativi).
Passanti9 fa notare come Guarini, nella Cupola della Sindone, sottolinei l’ascesa dalla zona terrena alla zona celeste creando nella prima un senso di irrequietezza mediante l’uso di poligoni con un numero dispari di lati e nella seconda un senso di riposo e serenità mediante l’uso di poligoni con un numero pari di lati e del cerchio.
Anche la Fisica è pervasa dalla Matematica (nei “Placita” si può leggere che tutto è numero, compresi il movimento e la luce) e, viceversa, la Matematica ha una sua entità fisica.
Galileo afferma che nel libro dell’universo la Filosofia è scritta in lingua matematica “e i caratteri son triangoli, cerchi ed altre figure geometriche (…) senza questi è un aggirarsi vanamente per un oscuro labirinto” e Guarini, nelle sue opere, crea un affascinante labirinto matematico in cui ogni simbolo ha un significato.
Uno dei temi guariniani più ricorrenti è proprio l’intreccio delle strutture, con la sua valenza geometrica ed astronomica. Ad esempio le volte più elementari, come quella della sala del Palazzo di Racconigi, trovano corrispondenza nelle illustrazioni di problemi relativi all’intersezione di piani, mentre le volte più complesse, come quelle di S. Anna Reale e di S. Lorenzo, nelle illustrazioni di problemi relativi alle orbite celesti (fig.9).
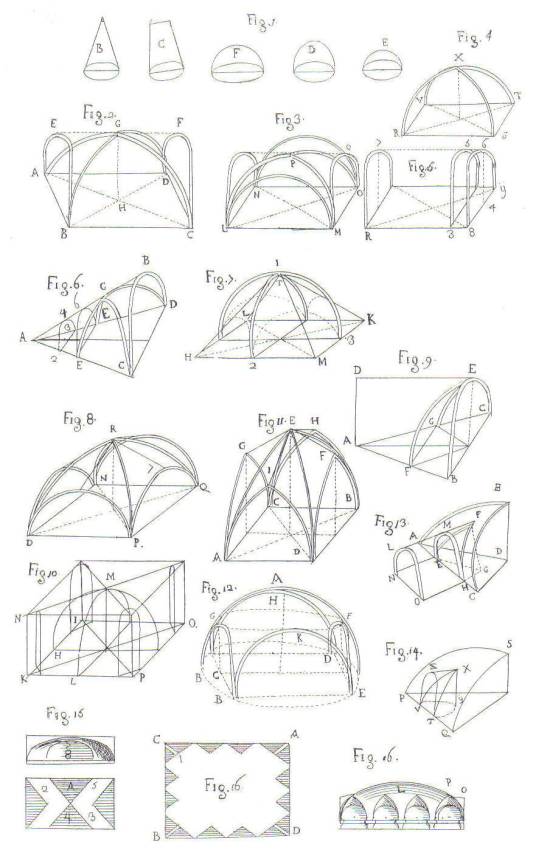
fig.9. Da “Architettura civile” (1968): tav. XXVII
La cupola, simboleggia il cielo e Guarini in essa non cerca la perfezione ma il movimento, perché dietro c’è Dio, il Dio degli Occasionalisti, causa di tutte le cose e di tutti i moti.
Nelle cupole si trovano riferimenti alle dissertazioni dei trattati matematici su coni e sezioni coniche: proprio la cupola della Sindone, il cui andamento è determinato da una successione di cilindri di dimensioni via via decrescenti, richiama alcune figure dell’”Euclides”.
Tornando all’Astronomia, Guarini, pur considerando l’uomo misura di tutte le cose e la Terra al centro dell’universo, studia il moto delle sfere celesti, le dipendenze reciproche fra gli astri. In campo architettonico ciò traspare dall’importanza attribuita non tanto ad un centro assoluto, quanto alle relazioni fra centro e periferia: si pensi alle compenetrazioni di ambienti collaterali, come avviene per gli atrii della Cappella della Sindone.
L’interesse per l’astronomia emerge anche dall’utilizzo delle stelle come elemento decorativo. Sul pavimento della Cappella della Sindone sono raffigurati cerchi concentrici di stelle (fig.1b) che richiamano le illustrazioni degli emisferi artico e antartico del “Coelestis mathematica”. Ma non basta: stelle si trovano nel reticolato delle lunette sotto il tamburo, stelle sono le croci nei pennacchi e una grande stella a dodici punte appare al culmine della cupola.
Un altro tema che affascina Guarini e al quale è dedicato ampio spazio in diversi suoi scritti, è quello della misurazione del tempo. Alcuni studiosi interpretano la cupola di S. Lorenzo come un grande orologio solare e il suo tamburo come una rappresentazione delle fasi lunari. Analogamente sono state evidenziate delle affinità (forse un po’ forzate) tra l’impianto planimetrico della Cappella della Sindone e i disegni dei trattati “Placita” e “Leges temporum et planetarum” che illustrano le fasi delle eclissi: secondo i sostenitori di questa tesi1 le posizioni della Luna potrebbero corrispondere a quelle dei vestiboli e tale corrispondenza non sarebbe casuale poiché il tema astronomico risulterebbe legato alla funzione iconologica della Cappella.
Per Guarini gli astri si muovono nel cielo seguendo un percorso ondeggiante, sinusoidale e spiraloide (egli cerca di modificare il sistema tolemaico sostituendo alla complessa serie di cicli ed epicicli delle curve spiraliformi): di nuovo incontriamo figure geometriche arricchite di una valenza cosmica ed utilizzate come elementi architettonici a tutti i livelli, dalla decorazione agli impianti planimetrici.

fig.10. Cappella della Sindone: esterno della cupola (da Passanti, 1963)
Nella Cappella della Sindone la sinusoide viene impiegata sia all’esterno, nel profilo del tamburo (fig.10), sia all’interno della cupola, nei tori serpentini che salgono a zig-zag a collegare le aperture vetrate; inoltre, in un primo progetto riportato nell’”Architettura Civile” per la cuspide è prevista una terminazione a spirale, linea che meglio delle altre potrebbe simboleggiare il percorso dall’infinitamente piccolo all’infinitamente grande, sintetizzando la concezione guariniana.
Ad ulteriore conferma dello stretto rapporto fra Geometria e Architettura, la cupola della Sindone sembra rappresentare uno dei tanti problemi di “ortografia gettata” proposti nell’”Architettura civile” (fig.11), uno studio sul modo “di stendere in un piano una superficie sferica segata da’ circoli paralleli”, “di distribuire una sfera in molte superficie annulari”: nella realizzazione architettonica tale sfera sembra aprirsi, sfrangiarsi, ridursi a brandelli.
In Guarini l’”imprevisto” e lo “stupefacente”5 sono sostenuti da regole tratte dalla geometria euclidea e applicate in modo assolutamente personale.
Non è possibile scindere l’architetto dal matematico poiché l’elemento fantastico e quello razionale sono così strettamente collegati ed interdipendenti da agire l’uno sull’altro contemporaneamente come controllo e sollecitazione6. Nella visione filosofica dell’architetto modenese, influenzata dall’Occasionalismo (Guarini legge il “Traité de l’homme” di Cartesio), Dio è considerato unico creatore ed unica causa reale e l’artista, derivando la propria capacità creativa dagli stimoli che la matematica ed in particolare la geometria esercitano sull’intelletto, esprime la propria libertà attraverso la scelta dei mezzi, dei materiali, delle tecniche, delle regole matematiche da utilizzare per la realizzazione delle proprie opere.
Il ricorso alla Geometria, all’intreccio delle linee, al contrasto degli spazi è dunque manifestazione del misticismo di Guarini, manifestazione di un pensiero che fonde astrazione matematica e speculazione teologica in nome di un comune denominatore: i concetti di Assoluto e di Infinito.
Note bibliografiche:
1. AAVV, “Guarino Guarini e l’internazionalità del Barocco”, Atti del Convegno Internazionale, Accademia delle Scienze di Torino, 1968.
2. Argan G.C., “L’architettura barocca in Italia”, Garzanti, 1957.
3. Boyer, “Storia della matematica”, Oscar Mondatori, 1980.4. De Bernardi Ferrero D., “I Disegni d’Architettura Civile et Ecclesiastica di Guarino Guarini e l’arte del maestro”, Albra, 1966.
5. Griseri A., “Le metamorfosi del Barocco”, Einaudi, 1967.
6. Guarini G., “Architettura civile”, Il Polifilo, 1968.
7. Guarini G., “Euclides adauctus et methodicus”, Augustae Taurinorum, 1671.
8. Kline M., “Storia del pensiero matematico”, Einaudi, 1991, vol.1.
9. Meek H.Q., “Guarini Guarini”, Electa, 1991.
10. Passanti,“Nel mondo magico di Guarino Guarini”, Toso, 1963.
11. Wittkower R., “Arte e architettura in Italia: 1600-1750”, Einaudi, 1972.
