H come Hamilton! Parliamo di quaternioni

Il Royal Canal di Dublino è, oggi, un placido corso d’acqua alla periferia della città. Le sue acque scorrono tranquille tra cespugli di giunchi, radi pontili e casette di pescatori. I germani reali e le anatre lo hanno eletto quale domicilio favorito. Un posto bucolico e ameno, che nessuno potrebbe sospettare sede di eventi drammatici o epocali.

Eppure uno dei suoi ponti più noti -il Broome Bridge- è meta, da alcuni decenni, di un discreto ma continuo flusso di turisti. Turisti che sono alla ricerca di una lapide commemorativa, posta nel 1958 e che riporta una curiosa iscrizione.

La lapide è una viva testimonianza di una celebre passeggiata, destinata a lasciare una forte impronta nella storia della Matematica e nelle scienze applicate.

Un piovoso lunedì di ottobre -il 16 per la precisione- del 1843 un trentottenne, celebre e affermato fisico-matematico irlandese, William Rowan Hamilton e sua moglie Helen si stanno, infatti, recando ad un congresso della Royal Irish Academy e, malgrado l’insistente chiacchiericcio della moglie, il giovane scienziato è completamente assorto nei suoi pensieri.

Sono anni che Hamilton si arrovella su un problema apparentemente insolubile: come estendere in R³ il concetto di numero complesso. Evidentemente, le parole di Helen non devono disturbarlo più di tanto perché -improvvisa e folgorante- ecco arrivare l’intuizione geniale. Il momento richiede tutta l’urgenza del caso e Hamilton si precipita a incidere sulle pietre del ponte la celebre formula:

i² = j² = k² = ijk = - 1

che segna, in modo forse ... un tantino romanzesco e romantico, la nascita del concetto di quaternione.
La Matematica contemporanea riconosce i quaternioni come una estensione del campo dei complessi. In generale, un quaternione è una combinazione lineare delle unità dei quaternioni 1, i, j, k, esprimibile in modo unico come:

a+bi+cj+dk 

con a, b, c, d coefficienti reali; a è definito scalare, mentre gli altri coefficienti costituiscono il vettore.

Nell’insieme H dei quaternioni -ancora oggi i quaternioni sono sostanzialmente indicati con questa lettera in onore di Hamilton- su cui definiamo due operazioni: la somma e il prodotto. La somma, come avviene per i complessi, si realizza attraverso la somma dei coefficienti:

q+q’ = (a, b, c, d,) + (a’, b’, c’, d’)=(a+a’, b+b’, c+c’, d+d’)

Il prodotto è, invece, definito dalla seguente tabella moltiplicativa (per le unità dei quaternioni):

quindi:

qxq’=(a, b, c, d,) x (a’, b’, c’, d’)=
=(aa’-bb’-cc’-dd’, ab’+ba’+cd’-dc’, ac’+ca’-ba’+db’, da’+ad’+bc’-cb’)

La prima osservazione che sorge spontanea è che il prodotto, così definito, non gode della proprietà commutativa e che quindi su H può essere definita, per mezzo delle operazioni predette, solo una struttura algebrica non commutativa.
Con la sola moltiplicazione, H assume la struttura di gruppo non abeliano, di cui rappresenta storicamente uno dei primi esempi.
La mancanza di questa proprietà fu un argomento assai duro da digerire per i coevi di Hamilton, poiché rappresentava una novità assoluta e, per molti, sconcertante nella storia della Matematica.
Il prodotto tra quaternioni, così definito, porta ad una seconda sorprendente proprietà: i polinomi definiti in H possono avere un numero di zeri superiore al loro grado!

L'insieme H, con la precedente operazione di somma e con la consueta operazione di prodotto con un numero naturale diviene invece uno spazio vettoriale in R⁴, con 1=(1,0,0,0); i(0,1,0,0); j(0,0,1,0); k(0,0,0,1) base canonica.

All’epoca della passeggiata sul fatidico ponte, Hamilton era un famoso e affermato matematico, così stimato da essere stato nominato docente di Astronomia, al prestigioso Trinity College, all’età di soli 22 anni.

Bambino prodigio nello studio delle lingue, si era precocemente segnalato -all’età di 13 anni- per aver scoperto un errore nella celeberrima Mécanique céleste di Laplace. L’impressione destata da tale scoperta fu tale da spingere l’Astronomo Reale d’Irlanda, John Brinkley, ad affermare:
This young man, I do not say will be, but is, the first mathematician of his age.

Hamilton si occupò della formalizzazione matematica delle leggi della Meccanica, in un continuo tentativo di generalizzare risultati precedentemente acquisiti. A lui è dovuta la generalizzazione dei risultati della meccanica newtoniana, attraverso le celebri equazioni di Hamilton e la funzione hamiltoniana.
A partire dal 1843, Hamilton si dedicò tuttavia ai soli quaternioni, abbandonando ogni altro studio. Alcuni mesi dopo la morte, avvenuta il 2 settembre 1865 all’età di sessant’anni, fu pubblicato un suo poderoso volume di 800 pagine, dal titolo Elementi sui quaternioni, a riprova di un interesse mai sopito!

Ritornando allora ai quaternioni, essi possono essere scritti anche facendo ricorso alle matrici complesse 2 x 2:

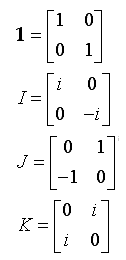
dove 1, I, J, K rappresentano la base predetta (i caratteri maiuscoli sono stati utilizzati per evitare confusioni con i l’unità immaginaria; 1 rappresenta la matrice identità). È semplice verificare che:

I²=J²=K²=-1

e che, dunque, I, J, K sono le tre differenti soluzioni dell’equazione: X²=-1
Analogamente a quanto accade per i numeri complessi, anche tra i quaternioni è definito il concetto di coniugato. Dato il quaternione q= a+bi+cj+dk, si definisce coniugato di q il quaternione
q segnata=a-bi-cj-dk.
Vale la pena di ricordare che H contiene, come sottoinsiemi, sia i numeri complessi che quelli reali, i primi sono i quaternioni della forma (a, b, 0, 0), mentre i reali sono i quaternioni della forma(a, 0, 0, 0).

Uno degli aspetti della Matematica che la rendono affascinante, per lo meno agli occhi ... dei matematici, è la possibilità di vedere così utilizzati nei più disparati ambiti applicativi oggetti e teorie matematiche nati per scopi meramente speculativi e assai distanti, anche nel tempo, da ogni apparente applicazione. I quaternioni non fanno eccezione. Di certo, Hamilton non avrebbe mai immaginato di vedere le proprie creature applicate nella computer graphic (si pensi alla rappresentazione frattale dell’insieme di Mandelbrot e dell’insieme di Jiulia, da cui deriva), nella teoria del controllo, piuttosto che nella meccanica orbitale o nella definizione di frattali (in particolare nella rappresentazione di rotazioni tridimensionali).

Chi ha dimestichezza, per esempio, con la Meccanica quantistica, avrà notato la notevole somiglianza delle matrici precedenti con le matrici di Pauli per la descrizione dello spin, generalmente indicate con σx, σy, σz e così definite:

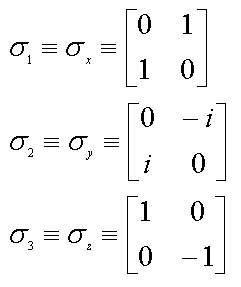
Esse formano, con l’aggiunta della matrice identità, una base nello spazio delle matrici.

Quello che abbiamo appena festeggiato, il 16 ottobre, è quindi il compleanno di un “signore” anzianotto ma che gode di ottima salute e grande vitalità!