Il triangolo: che meraviglia!

Altro che meraviglia! il triangolo ... che noia! dice un povero studente alle prese con uno di quei terribili problemi: "Calcolare gli angoli di un triangolo sapendo che l'altezza relativa ..." giustamente, il famoso comico Walter Waldi, si chiedeva: "ma chi è che va in giro a costruire quadrati sull'ipotenusa?"

PUNTI DI VISTA

Per un verso i triangoli, tranne quelli particolari (rettangoli o isosceli), sembrano tutti uguali. Certamente, non tanto quanto le circonferenze che riconosci ovunque. In realtà sono anche tutti diversi, visto che le proprietà che li riguardano sono una quantità enorme. "Che meraviglia che una figura semplice come il triangolo sia tanto inesauribile nelle sue proprietà" diceva il matematico August Crelle nella prima metà dell' 800, in un periodo in cui fiorivano gli studi sulla cosiddetta "Geometria del triangolo”. Basta che un angolo, dotato di ben poche proprietà, si chiuda con un terzo Iato e le proprietà diventano moltissime. La figura porta con sé un'infinità di aspetti curiosi, talvolta anche molto facili da dimostrare, altre volte complicati.

E, quando si dice che il triangolo è "la forma piana più semplice, si intende proprio questo: se dal triangolo si toglie anche un solo elemento - vertice o Iato - tutte le proprietà scompaiono o, peggio, diventano banali. Certamente, nell'educazione matematica moderna, si sta perdendo il senso geometrico delle figure e dello spazio che occupano. Per recuperarlo sarebbe utile senz'altro recuperare la coscienza che gli oggetti della Geometria sono, o sono stati, forme spaziali, da considerare per il loro aspetto. Il calcolo e la deduzione, gli strumenti dell'Analisi e dell'Algebra, sono un potente metodo d'indagine per numerosi fenomeni della Matematica, ma la visione sintetica legata alla percezione immediata (e anche il senso estetico) è all'origine di quella parte della Matematica che indaga le forme dello spazio. Questa rappresenta ancora oggi un potente metodo di conoscenza e una fonte di materiale educativo.

IL TRIANGOLO PRESO SUL SERIO

Allora guardiamo al triangolo, un triangolo qualsiasi, proprio come a una forma elementare. Per accorgerci che non compare mai da solo, ma sempre accompa gnato da un certo numero di punti, rette, circonferenze... o figure che gli sono col legate in maniera naturale e lo accompagnano nella scoperta delle sue proprietà o delle loro dimostrazioni. Questo è un fenomeno comune in Matematica: se volete studiare un certo ente, non potete isolarlo dal suo ambiente e da enti fatti della sua stessa materia, che gli rimangono collegati. Almeno se volete scoprire qualche fatto interessante. Talvolta sono proprio questi enti ausiliari che permettono di esprimere le proprietà e capirle più profondamente.

Per esempio, nel caso del triangolo, forse la prima e più semplice proprietà è questa: ogni triangolo si può inscrivere in una circonferenza.

È una proprietà di cui ci si rende conto facilmente: basta considerare gli assi dei tre Iati, vale a dire le rette che passano perpendicolarmente per i punti medi dei Iati. Ciascun asse è luogo dei punti equidistanti da due vertici. Il punto O di intersezione di due assi è dunque equidistante dai tre vertici del triangolo. Ne segue che esiste una (per forza unica) circonferenza che passa per i tre vertici o, come si dice, circoscritta al triangolo, di cui O è il centro. Per questo Osi chiama circocentro: è ovvio che anche il terzo asse passi per O.

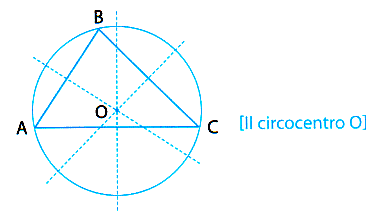
Non è mai un fatto banale scoprire che tre rette, costruite in maniera indipendente l'una dall'altra, concorrono in un punto.
Per questo il circocentro O è il primo dei punti note voli del triangolo. Questa terminologia fu introdotta da un matematico tedesco, Georg Klügel, all'inizio dell'800.
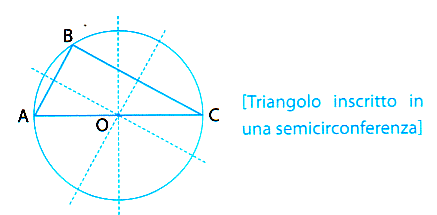
Dallo studio dei punti notevoli, vengono informazioni interessanti relativamente all'intero triangolo. Per esempio, sappiamo che, secondo uno dei primi risultati della moderna cultura geometrica, associato al nome di [TALETE DI MILETO], un triangolo inscritto in una semicirconferenza è retto.

Dunque, se il circocentro si trova su un Iato del triangolo, l'angolo opposto è un angolo retto. Altre proprietà si vedono subito. Per esempio: se il circocentro è interno al triangolo allora il triangolo è acutangolo, altrimenti è ottusangolo.

In maniera analoga al circocentro (una maniera che i matematici in realtà considerano "duale" della precedente) si costruisce un altro punto notevole, l'incentro I, per scoprire che ogni triangolo si può circoscrivere a una circonferenza. Per questo, basta considerare l'intersezione I delle bisettrici di due angoli: come luogo dei punti equidistanti dai lati, I è il centro di una (unica) circonferenza tangente a tutti e tre i Iati: e la terza bisettrice passerà per forza per I (dovrebbe anche essere chiaro – almeno intuitivamente – in che senso le due costruzioni, del circocentro O e dell'incentro I, sono da considerare"duali").

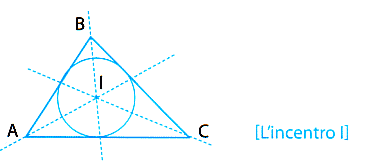
Così la figura"triangolo"si arricchisce di due [PUNTI NOTEVOLI] e delle rispettive circonferenze. Altri punti notevoli del triangolo, noti fin dall'antichità, meritano una considerazione. Non sono solo i tre assi dei lati o le tre bisettrici degli angoli che godono della proprietà particolare di concorrere in un punto (che in generale sarà diverso, tranne che nello specialissimo caso del triangolo equilatero).
È noto che la stessa proprietà vale per le altezze relative ai tre lati (tracciate, ciascuna, dal vertice opposto) e anche per le tre mediane, vale a dire le rette che congiungono un vertice del triangolo con il punto medio del lato opposto. Questi punti si chiamano rispettivamente ortocentro (l'intersezione delle altezze, denotata solitamente con H) e baricentro (o centroide, l'intersezione delle mediane, denotata con G).
In particolare, G sta per gravità perché il nome esprime anche la proprietà caratteristica del punto: quella di essere il "centro di gravità": se pensate a un triangolo fatto di materiale omogeneo e lo sospendete in questo punto G, allora il triangolo rimane in equilibrio, senza sbilanciarsi da una parte o dall'altra. È un fatto che ha da sempre attirato l'attenzione, fin dal periodo classico, proprio per il legame che istituisce fra una figura ideale, in questo caso una figura piana, e la sua concreta proprietà fisica di rimanere in equilibrio.
Ma, nei casi dell'ortocentro e del baricentro, la dimostrazione non è immediata. Non si capisce "al volo" perché le tre altezze, o le tre mediane, si debbano incontrare in uno stesso punto.

IL BARICENTRO

Cominciamo a cercare il baricentro del segmento AB, pensato come un'asta materiale. Dove si trova? A mezza strada, si dirà. E infatti è vero.
O, per lo meno, è vero se si pensa che il segmento AB sia fatto di materiale omoge neo o, che è lo stesso, che sugli estremi A e B ci sia lo stesso carico q. In questo caso si può pensare, in maniera equivalente, che il punto medio M sia caricato con 2q. Se invece su A si pone il carico a e su B il carico b, le cose sono diverse. È chiaro che il baricentro, in questo caso, si trova nel punto N, interno al segmento AB, che soddisfa la seguente relazione (detta regola del momento):

a•BN=b•NA

(dove BN e NA sono le misure dei segmenti, rispetto a una qualsiasi unità di misura). In questo caso, si può pensare che N sia caricato con a+b.

Torniamo all'oggetto della nostra discussione, il triangolo, che abbiamo momen taneamente abbandonato a favore del baricentro di un segmento.

Dunque, se pensiamo che i tre vertici del triangolo ABC siano caricati in maniera uguale o, che fa lo stesso, che il triangolo sia di materiale omogeneo, rispetto al l'equilibrio del triangolo è equivalente considerare il segmento MC, pensando che M abbia un carico doppio di C (perché"sopporta" sia A che B).

Allora, allo scopo di rispettare la regola del momento, il centro di gravità del triangolo si troverà sulla mediana CM, spostato di 2/3 da C e di 1/3 da M. L'abbiamo trovato e non c'è nessun motivo di ritenere che non sia unico: un minimo di riflessione ci convince che si tratta dell'unico centro di gravità del triangolo: pensate di spostarvi anche poco da questo punto di equilibrio....
Ma allora, anche se la costruzione viene fatta a partire dal vertice A e dal punto medio del lato BC, op pure a partire da B e dal punto medio di AC, si deve trovare lo stesso punto G.
Quindi le tre mediane concorrono in un punto, che le divide, ciascuna, nel rapporto 2/3 - 1/3.
Questo punto è proprio il baricentro G.

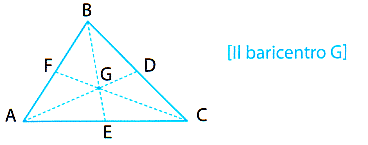
Ora, prima di passare all'ortocentro, un utile esercizio consiste nel rendersi conto che, se si prende il triangolo mediano, che ha per vertici i punti medi DEF del triangolo dato, il baricentro è lo stesso.

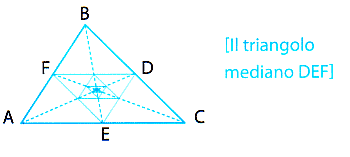
L'ORTOCENTRO (E LA RETTA DI EULERO)

Il triangolo mediano, appena proposto come esercizio, ci permette di scoprire abbastanza facilmente un'altra singolare proprietà dei triangoli e, allo stesso tempo, di dimostrare alla fine che le tre altezze del triangolo si incontrano in uno stesso punto, l'ortocentro.
A questo scopo, dobbiamo ricorrere a un aspetto che spesso i matematici considerano: la dinamica delle figure.
La figura non rimane lì, immobile nel proprio spazio, ad aspettare le indagini dei ricercatori. La figura può essere mossa, grazie a opportune trasformazioni, e rivelare in questo movimento alcune proprietà nascoste. In questo caso, consideriamo la trasformazione che porta ogni punto P, interno al triangolo (compreso quelli che stanno sui lati) nel punto P', univocamente determinato dalla proprietà:

P' si trova sulla retta PG (G è il baricentro), dall'altra parte di G rispetto a P, a distanza da G uguale alla metà di PG.

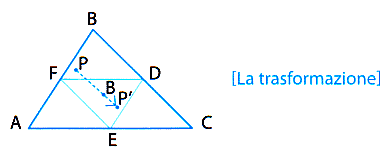
È chiaro che, dato che sia P, questa regola permette di individuare precisamente P', con la sola eccezione del corrispondente di G, il quale, per definizione viene fatto coincidere con G stesso: G' = G. In questa maniera, tutto il triangolo ABC, per così dire, si rovescia e si comprime nel triangolo mediano DEF. In particolare, i vertici vengono trasformati nei punti medi dei lati opposti: A'= D, B'= E e C'= F e la trasformazione fornisce una corrispondenza biunivoca fra i punti del triangolo dato ABC e del suo triangolo mediano DEF.
La corrispondenza inversa, che a ogni punto di DEF associa un punto di ABC, si ottiene con la stessa regola ma tenendo conto che, per avere la distanza da G, si dovrà moltiplicare per 2 anziché dimezzare.
C'è solo qualche verifica da fare, prima di mettere in moto la trasformazione e dimostrare quello che ci interessa. Non è molto difficile: occorre verificare che un segmento interno al triangolo ABC venga trasformato ancora in un segmento (na turalmente interno al triangolo mediano DEF) e poi che i due segmenti, quello dato e il suo trasformato, siano paralleli.

Ora, verificate che le altezze del triangolo ABC vengano trasformate nelle altezze del triangolo mediano (facile), ma... attenzione: le altezze del triangolo mediano coincidono con gli assi di ABC.
Dunque, poiché gli assi hanno un punto in comune, il circocentro O di ABC, e in quanto altezze di DEF corrispondono alle altezze di ABC, anche queste altezze si intersecano in un punto: l'ortocentro H. Non solo, ma il fatto che il circocentro di ABC coincida con l'ortocentro di DEF ci dice anche che i tre punti notevoli del triangolo – "baricentro" G, "ortocentro" H e "circocentro" O – stanno su una stessa retta: infatti, nella trasformazione considerata, punti come H e O – che si corrispondono – sono per definizione allineati con G.
È così dimostrato un bel teorema, senza che sia richiesta una qualche ipotesi particolare:
in ogni triangolo il baricentro, l'ortocentro e il circocentro sono allineati. B

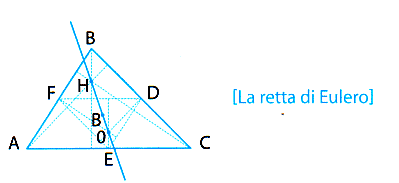
E, a partire dal triangolo, la figura si arricchisce (senza complicarsi) di una retta che d'ora innanzi lo accompagna nelle considerazioni. Questa retta, associata in trinsecamente a ogni triangolo, si chiama retta di Eulero, dal nome del famoso matematico del '700 [LEONHARD EULER].

IL TEOREMA DI CEVA (E QUELLO DI MENELAO)

Si è detto che non è mai banale la scoperta che tre rette, a priori costruite in maniera indipendente, concorrono in uno stesso punto oppure similmente che tre punti, apparentemente scollegati nei loro rapporti, sono in realtà allineati. Un teorema del '700, ricordato con il nome del matematico, fornisce una condizione necessaria e sufficiente affinché tre rette, ciascuna uscente da uno dei vertici di uno stesso triangolo, siano concorrenti (cioè passino per uno stesso punto). In maniera analoga, vale un risultato che caratterizza esattamente il fatto che tre punti che si trovano sui lati di un triangolo (o sul loro proseguimento), siano allineati.

Teorema di Ceva. Dato un triangolo ABC, si considerino tre rette (uscenti ciascuna da un vertice) e siano D, E e F i punti di intersezione, rispettivamente, con i Iati opposti (per comodità supponiamo che D, E e F siano interni ai rispettivi Iati). Le tre rette si incontrano in un punto se e solo se vale la seguente condizione:

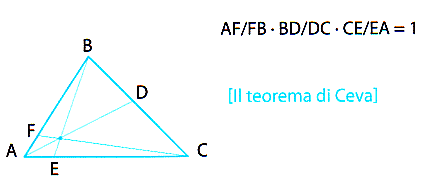
La dimostrazione? Non è troppo diversa da quella che ci ha fornito il baricentro G del triangolo. Infatti, basta pensare che i vertici A, B e C del triangolo siano caricati in maniera diversa – diciamo con pesi a, b e c, o se volete che il materiale di cui è costituito il triangolo non sia omogeneo – e poi calcolare il baricentro dell'oggetto che si ottiene in questo modo. Nel caso "omogeneo"; i tre rapporti fra segmenti che compaiono nella formula precedente valgono tutti 1, perché F è il punto medio di AB e lo stesso vale per gli altri lati (e quindi il loro prodotto vale 1). Nel caso generale questo non è vero, ma le considerazioni sono dello stesso tipo... con qualche calcolo in più.

Anche la condizione che le tre rette concorrenti si incontrino internamente al triangolo non è una vera limitazione: quando le intersezioni avvengono sui proseguimenti dei lati, per le misure dei segmenti bisognerà tener conto del segno. Questo fenomeno si capisce forse meglio, almeno intuitivamente, se si considera il "duale" del teorema di Ceva, che riguarda l'allineamento di punti situati sui lati del triangolo: in questo caso almeno uno dei punti deve essere senza dubbio sul proseguimento di un lato. II teorema prende il nome da, famoso matematico e astronomo del I secolo.

Teorema di Menelao. In un triangolo ABC siano dati tre punti D,E e F, ciascuno su uno dei Iati (o sul prose­ guimento di un lato). I tre punti D, E e F sono allineati se e solo se

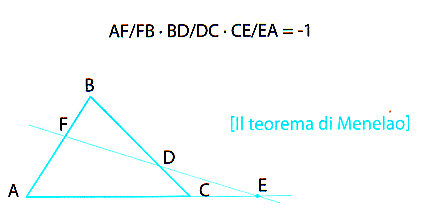
Vista la differenza di segno? E se ora volete fare un esercizio più complicato... eccolo qua: in un triangolo qualsiasi, costruite l'ortocentro H; ora costruite i cosiddetti excentri, cioè i centri delle tre circonferenze che, essendo esterne al triangolo, sono tangenti a un lato e al proseguimento degli altri due lati (queste sono i cosiddetti excerchi). Con gli excentri avete ottenuto un nuovo triangolo, di vertici E1, E2 ed E3 . Dimostrate che l'ortocentro di questo nuovo triangolo è ancora H. Buona fortuna!