Invito alla crittografia

I PROBLEMI

Nella letteratura moderna che riguarda la Crittografia - allo scopo di illustrare i problemi ed i metodi fondamentali - sono stati introdotti due personaggi fittizi, Alice e Bob, ormai diventati tradizionalmente i protagonisti dell'azione. La loro origine è chiaramente dovuta ad una personificazione delle lettere A e B usate nel linguaggio formale dei ricercatori. Il fatto che due simboli siano diventati dei personaggi, ai quali i testi assegnano ormai un volto - e con qualche dose di sfacciataggine, anche un carattere sia pure embrionale sta forse a significare, al di là del gioco, che la materia si presta ad un'applicazione immediata e pretende un contesto nel quale si possano riconoscere direttamente e non astrattamente i contendenti o, di volta in volta, gli alleati di una competizione.
Ad esempio: Alice e Bob hanno litigato e si dividono tutti i beni acquisiti in comune. Per alcuni oggetti la scelta è facile, mentre per altri si impone un sorteggio per decidere a chi assegnarlo. Ma i due non intendono incontrarsi (oppure si trovano ormai a chilometri di distanza) e vogliono effettuare il sorteggio per telefono. Chi dei due sarà così generoso -e fiducioso- da lasciare che l'altro tiri la classica moneta e gli comunichi l'esito del sorteggio?

La situazione è delicata, rischia di rinfocolare i dissapore peggiorare i rapporti ma... niente paura: entrambi possono convenire su un metodo che garantisce a ciascuno cinquanta per cento di probabilità (cioè un sorteggio equo) senza doversi fidare dell'altro, pur di avere un minimo di conoscenze della complessità computazionale di certe operazioni aritmetiche sui numeri interi. Alice e Bob sono fortunatamente preparati su questo argomento ed il problema è risolto.
Un altro problema vede invece Alice e Bob desiderosi di scambiarsi messaggi - non importa di che natura anche se tutti concordano che siano affettuosi. Ma la loro sorte è, ahimé, anche in questo caso, di essere a grande distanza e per questo vogliono accordarsi su una chiave che serva a cifrare il reale contenuto dei messaggi: diciamo che Charlie, uno spasimante rifiutato da Alice, potrebbe altrimenti servirsene per mettere in difficoltà il loro rapporto. Anche qui niente paura: Bob ha frequentato un corso sulla Crittografia a chiave pubblica e spiega ad Alice per telefono, in maniera chiara, come possono procedere. Charlie intercetta il messaggio e capisce che non potrà attuare il suo programma di disturbo. Anche lui ha seguito lo stesso corso sulla Crittografia e gli è evidente che, pur intercettando le loro comunicazioni, non potrà venire a conoscenza della chiave crittografica che Alice e Bob intendono convenire per scambiarsi i messaggi.
Prima che una disciplina scientifica, la Crittografia era una pratica, un insieme di regole, di metodi, di strumenti. Era diventata quasi un'arte: l'arte di scambiarsi i messaggi senza farne capire il reale contenuto, anche se venivano intercettati. Una disciplina dallo statuto ambiguo, al limite della magia e dell'esoterismo. In questo contesto, Alice e Bob non sono ancora nati. Si ha a che fare con problemi di spionaggio, di nemici desiderosi di venire a conoscenza delle informazioni che scambiamo con i nostri alleati, per servirsene a nostro danno.
Si capisce che l'origine è antica, legata non solo ad esigenze commerciali, ma soprattutto diplomatiche e militari. È noto che in molti casi le sorti dei conflitti sono state decise da questa capacità di conoscere, con buon anticipo, le mosse dell'avversario. Poi, l'avvento delle reti di comunicazione digitale, utilizzate regolarmente nella vita quotidiana, ha richiesto nuove esigenze di sicurezza e di tutela della privacy. E la Matematica - in particolare la Teoria dei numeri - ha fatto cambiare natura alla Crittografia, liberandola dalla sua aura di mistero e trasformandola da un'arte in una scienza.
Ma che cosa hanno in comune, con questa secolare materia, i due problemi precedenti che coinvolgono Alice e Bob: un sorteggio effettuato per telefono o lo scambio di una chiave cifrante sotto il naso di chi la intercetta ma che non potrà mai farne uso? Il fatto è che, quando la Matematica mette le mani con la sua formalizzazione in qualche settore, allora rivela anche tutta una serie di problemi apparentemente diversi e non collegati che invece mostrano una definita e spesso profonda unità.

E questo è quello che è avvenuto abbastanza recentemente: il problema non è solo quello di (1) cifrare o decifrare un messaggio, ma anche quello di "certificarlo", vale a dire: (2) riconoscere il mittente del messaggio e (3) rendersi conto se il messaggio è integro oppure durante la trasmissione è stato manipolato. Ma anche: (4) accordarsi con qualcuno su un dato da mantenere segreto, pur usando un canale di trasmissione non sicuro; (5) prendere una decisione a sorte, con uguali probabilità di successo rispetto ad un interlocutore non fidato; (6) far sapere che si dispone di una certa conoscenza, senza rivelarne la fonte o il segreto.
Il primo dei problemi elencati è quello della sicurezza della trasmissione, al quale ci hanno abituato numerosi film di guerra e di spionaggio. Il secondo è quello della autenticità del mittente; in questo caso, oltre al doppio gioco delle spie, conviene ricordare i problemi moderni di transazione economica a distanza: il bancomat o la cosiddetta firma digitale che ci permette di essere riconosciuti anche per posta elettronica. Il terzo dei problemi menzionati riguarda la integrità del messaggio; è una insidia che ha precedenti famosi: Romeo si rifugia a Mantova e riceve dalla fidata nutrice (si fa per dire!) la notizia falsa che Giulietta è morta, con tutto quel che ne segue. I problemi (4) sorteggio a distanza e (5) scambio della chiave sono quelli in cui abbiamo già visto all'opera Alice e Bob e la cui soluzione sarà svelata più avanti. L'ultimo problema elencato si rivolge alla cosiddetta conoscenza zero: come garantire di possedere un'informazione senza rivelarne gli aspetti fondamentali? Ad esempio, come ha fatto Nicolò Fontana, il famoso Tartaglia, a far sapere nel `500 di aver scoperto la formula risolutiva per radicali delle equazioni di terzo grado senza doverla rivelare alla comunità matematica (almeno finché c'è riuscito)? In questo caso, il problema non è difficile: basta mostrare di saper calcolare le radici di alcune equazioni proposte da altri. Chiunque può facilmente verificare che la risposta è corretta e convincersi dopo qualche esibizione del genere che chi ha trovato le radici delle equazioni deve per forza avere un metodo sicuro, una formula per l'appunto: verificare se un certo numero è una radice è una operazione ben più semplice che trovarlo, almeno per chi non conosce la formula. Ma pensate invece di aver fatto una invenzione per la quale chiedete un finanziamento allo scopo di brevettarla: un'occhiata al progetto è sufficiente per carpirvi l'idea e si capisce che l'idea è tutto. Allo stesso tempo, volete che il vostro finanziatore sia certo che il meccanismo funziona. Fidarsi, oppure no? Quale via seguire?
È chiaro che, per questa strada, i problemi si moltiplicano. Per la maggior parte di loro, la pratica ha trovato delle soluzioni empiriche, speciali e diverse da caso a caso. La Matematica cerca di vedere tutti questi problemi come casi particolari di uno solo, fondamentale.

Gli uomini hanno dapprima creato le parole allo scopo di capirsi l'un l'altro e poi - forse pentiti - hanno inventato la Crittografia per farsi capire solo da alcuni. Ma in questo modo, oltre a sollecitare la curiosità spesso interessata degli esclusi, si sono dovuti rifugiare in un mondo di segreti da condividere con poche persone. La nuova e moderna versione della Crittografia, quella che viene detta a chiave pubblica, sembra nata dal desiderio ecumenico dei matematici di trattare tutti allo stesso modo, curiosi e confidenti, sottraendo dalle nostre comunicazioni private anche la più piccola condivisione del segreto. Con quale successo, si vedrà.

Prima di approfondire le idee ed i metodi fondamentali è bene però fare un'osservazione di principio: nel problema classico della trasmissione del messaggio, da Alice a Bob, con il tentativo di uno come Charlie di decifrarne il reale contenuto - problema che si presta a incorporare entro di sé tutti gli altri, che ne diventano aspetti particolari o specializzazioni - si è soliti assegnare un comportamento legittimo a chi cerca di comunicare, mentre l'intercettatore è visto sotto una luce negativa, come una persona che in maniera indebita non si fa "gli affari suoi". Niente di più sbagliato, per quanto riguarda questa attività: ad esempio, è noto che uno dei più famosi casi di uso delle tecniche crittografiche si è avuto nel corso della seconda guerra mondiale, quando il servizio segreto inglese, con l'aiuto essenziale di Alan Turing (1912-1954), è riuscito a decrittare fin dal 1942 la macchina cifrante Enigma, usata dal comando tedesco. E questo fatto è risultato decisivo per le sorti della guerra (anche se un'altra macchina, la T-52, rimase in funzione per tutta la guerra).
È con questo spirito di obbiettività che i crittografi ed a maggior ragione i matematici si prestano a considerare i loro metodi: la storia della Crittografia è piena di mosse e contromosse, una sorta di competizione fra chi inventa sempre nuovi procedimenti di cifratura e chi implacabilmente trova la maniera per decrittare anche il nuovo sistema.
Chi cifra e chi decifra sono da considerare sullo stesso piano. Si tratta di due modalità diverse dello stesso fenomeno, come due segmenti le cui misure hanno segno diverso solo perché l'orientamento positivo della retta è stato scelto in un verso piuttosto che nell'altro. La considerazione morale del comportamento appartiene ad un altro contesto.

Brevi ed affascinanti notizie sulle vicende storiche e sulle idee moderne dell'attività crittografica dal punto di vista tecnico sono contenute in Sgarro [1] ed in Berardi, Beutelspacher [2]. Una trattazione più ampia ma sempre narrata in modo avvincente è quella di Singh [3]. Chi volesse inquadrare il problema dal punto di vista del suo impatto sullo sviluppo dei sistemi di comunicazione digitale - e quindi rispetto principalmente alle problematiche sociali e legali - potrà consultare Giustozzi, Monti e Zimuel [4].

LA CHIAVE CIFRANTE

Per quanto possa sembrare paradossale, tutti convengono che, per dotarsi di un metodo con il quale trasmettere dei messaggi riservati lungo un canale che può essere intercettato, è necessario avere in precedenza a disposizione un canale sicuro attraverso il quale A e B possono scambiarsi una chiave che serva all'uno per cifrare i messaggi ed all'altro per decifrare.

Il fatto è che questo canale sicuro non può essere usato per le normali trasmissioni, ma magari si stabilisce in condizioni eccezionali, difficilmente ripetibili. Ad esempio, nella metafora spionistica, che ben si adatta a queste situazioni, A e B si incontrano e si accordano direttamente sulla chiave che in seguito useranno. Basta. Il canale sicuro fornito dalla loro vicinanza e dalla possibilità di comunicare a voce non si ripeterà più, ma la chiave rimane a garanzia della segretezza per le loro future comunicazioni lungo un altro e più consueto canale che -ben lo sanno- è sistematicamente intercettato dal rivale C.

Il ruolo fondamentale della chiave cifrante è stato addirittura codificato in un periodo in cui l'attività crittograrica, da sempre in grande uso nel campo militare, ha raggiunto una specie di massimo impiego. Il filologo olandese Jean Guillaume Kerckhoffs (18351903), nella sua opera La cryptographie militaire del 1883, osserva che la sicurezza di un sistema crittografico dipende solamente dalla segretezza della chiave.
In altri termini, si ammette senza discussione che un eventuale intercettatore venga a conoscenza dei messaggi cifrati ed anche del sistema di cifratura usato: quello che non deve conoscere è la chiave. Sulla sua segretezza riposa la sicurezza della trasmissione e viceversa: all'intercettatore basta conoscere la chiave per essere in grado di decifrare tutti i messaggi.
Qual è allora il problema dal punto di vista di chi vuole scambiarsi messaggi riservati? Chiaramente, in primo luogo la chiave del sistema crittografico deve essere a conoscenza di poche persone, chi trasmette e chi riceve e possibilmente nessun'altro perché -si sa- gli intercettatori hanno pochi scrupoli. E poi unire il requisito della semplicità -per poterla ricordare senza lasciare in giro documenti in cui è possibile trovarla e per facilità d'uso- insieme a qualche forma di complessità che non consenta di risalire facilmente ad essa esaminando un certo numero di messaggi cifrati. Diciamo che i problemi della chiave crittografica sono quelli della sua condivisione fra più soggetti e di un equilibrato rapporto fra la semplicità e la complessità d'uso.

UN PO' DI STORIA

Secondo la Vita Caesarum di Svetonio, uno dei più antichi sistemi cifranti risale a Giulio Cesare e fu usato nella sua guerra contro i Galli. È noto che altri sistemi, spesso molto originali, erano stati usati anche in precedenza, ma questo di Cesare è forse il primo a non essere occasionale: propone un metodo, un sistema, è ripetibile con chiavi diverse.
L'idea è in verità così semplice che non rende onore alla perspicacia dei Galli, ma la assumiamo per comodità di esposizione: dopo aver disposto le lettere nel classico ordine alfabetico, considerato circolare -quindi, con la lettera a che segue la z- ciascuna lettera viene traslata a destra di una stessa quantità. Così, se la traslazione è di due lettere, la a diventa c, la b diventa d ... e così via, finché la z diventa b come nello schema seguente nel quale ogni lettera in chiaro è posta al di sopra della corrispondente lettera cifrata:

a b c d e f g h i l m n o p q r s t u v z
c d e f g h i l m n o p q r s t u v z a b

Tutte le lettere del messaggio vengono quindi ordinatamente cambiate nelle loro corrispondenti lettere cifrate. Questo è il cifrario di Cesare (o di traslazione) e l'informazione essenziale della chiave in questo caso è solo data dalla quantità che specifica il valore della traslazione: si hanno in tutto, evidentemente, 21 chiavi cifranti distinte - di cui una banale, l'identità.
Il criterio della semplicità è senz'altro soddisfatto. Forse fin troppo. E non è difficile pensare di passare da una traslazione ad una affinità, per aumentare un po' il numero di cifrari senza tuttavia rendere impraticabile il sistema. Questo vuol dire che invece di una formula del tipo:

n'=n+k

dove n rappresenta la posizione della lettera da cifrare, n' la posizione della corrispondente lettera cifrata (n, n' =1, 2, ... , 21) e k è la chiave, si userà un'espressione del tipo:

n'=an+b

In questo caso la chiave è data dalla coppia ordinata di interi (a, b), entrambi non superiori a 21. Non tutti i valori di a hanno però senso: se si vuole risalire univocamente dal testo cifrato a quello in chiaro, è necessario che sia MCD(a,21)=1 cioè che l'intero a non abbia divisori comuni con 21 (come si dice: a e 21 devono essere primi fra di loro). È facile calcolare (esercizio!) il numero di cifrari affini che sono distinti: si tratta di 252, uno dei quali è ancora l'identità.
Il numero di cifrari è maggiore di prima, ma sempre troppo basso per pensare di fronteggiare l'attacco di abili decrittatori. Una strategia potrebbe essere quella di assumere una permutazione qualsiasi per determinare le lettere cifrate, invece di usare una formula semplice come quella della traslazione o dell'affinità. Le permutazioni possibili sono 21! e questo è un numero che ha ben 20 cifre decimali e mette al riparo qualunque cifrario dal pericolo di essere infranto per tentativi. Ma non va bene. Perché chi trasmette e chi riceve dovrebbero registrare da qualche parte la permutazione delle lettere che hanno scelto, a scapito della segretezza: la chiave crittografica non è data da una informazione facile da ricordare, e di uso semplice, ma è tutta la permutazione stessa.
Il problema che si pone è allora questo: come generare una permutazione delle lettere dell'alfabeto mediante un meccanismo semplice da ricordare? Nella pratica questo problema ha dato luogo all'idea di parola chiave. A questo punto, dall'epoca di Cesare, siamo già arrivati al Rinascimento, quando le tecniche crittografiche -legate alla crescita dei commerci e dei contatti diplomatici fra gli Stati- risorgono da un periodo oscuro.
Presa una parola senza ripetizioni, si usano le sue lettere come le prime della permutazione da usare, a partire da un certo posto. Le altre lettere del cifrario vengono elencate successivamente, saltando quelle già usate. Ad esempio, con la parola chiave salve utilizzata a partire dalla lettera d, cioè dalla quarta posizione, si ottiene la permutazione seguente:

a b c d e f g h i l m n o p q r s t u v z
t u z s a l v e b c d f g h i m n o p q r

In questo caso la chiave crittografica si riduce alla coppia (salve, 4). Ma la storia non finisce qui: un decrittatore con buone conoscenze di Statistica, qualche tabella ed un numero sufficiente di messaggi cifrati, che A e B si sono scambiati, è in poco tempo in grado di risalire alla chiave. Naturalmente, conoscerà la frequenza con cui le varie lettere dell'alfabeto compaiono in testi della stessa natura di quelli che vuole decrittare -lettere d'amore o messaggi militari che siano- e distinguerà presto, ad esempio, le vocali e certe consonanti più usate dalle altre lettere. Il tutto con grande ambiguità, ma solo per il momento. Farà delle prove, metterà in atto delle congetture, tentativi più o meno motivati, fino a trovare una parola di senso compiuto o a riconoscere il periodo con cui avviene la cifratura: sostanzialmente la lunghezza della parola chiave.
A questo punto è fatta. Da qui ad infrangere tutto il cifrario il passo è breve.
Come annullare le frequenze statistiche ed evitare le ripetizioni periodiche? Si riconosce facilmente che l'analisi delle frequenze è resa possibile dal fatto che il cifrario è a sostituzione monoalfabetica, vale a dire che ogni lettera viene cifrata sempre con la stessa lettera nel corso, della trasmissione dell'intero messaggio. Questo inconveniente si può risolvere passando a cifrari a sostituzione polialfabetica, ad esempio usando cento simboli diversi, di natura qualsiasi, per cifrare le 21 lettere in chiaro. Se sappiamo ad esempio che nei messaggi che ci interessano la lettera a ricorre mediamente dieci volte su cento, basterà usare dieci simboli diversi per cifrarla. Niente paura: non è necessario che fra l'alfabeto in chiaro e quello cifrato ci sia una corrispondenza biunivoca, ma solo che sia univoco i: passaggio dal testo cifrato a quello in chiaro. In questo modo, la lettera a viene cifrata una volta in un modo e una volta in un altro in dieci maniere diverse e la sua frequenza è di fatto annullata: ma chi riceve il messaggio e conosce il sistema cifrante è in grado in ogni caso di riconoscere che ben dieci simboli diversi vanno interpretati come a.

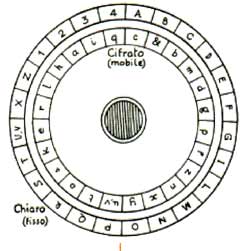
Disco cifrario

Si capisce però che il problema è risolto solo in parte in quanto, nel continuo alternarsi fra la ricerca della semplicità del sistema e la sua sicurezza, questo metodo richiede a chi trasmette e a chi riceve di dotarsi di una imponente tabella da consultare ogni volta. E questo fatto, pur fornendo in alcuni casi delle indicazioni utili, contraddice l'esigenza di segretezza della chiave.

Il prossimo passo, invece, individuato nel corso del `400 da alcuni studiosi rinascimentali ed esplicitamente proposto da quel grande artista e matematico che fu Leon Battista Alberti (1406-1472), risulta decisivo: nella sua opera Modus scribendi in ziferas del 1466, introduce una sostituzione polialfabetica facile da eseguire e che rende estremamente più difficili da cogliere i cicli che avvengono nella cifratura e quindi le periodicità del cifrario. Questa idea rimarrà in funzione, sostanzialmente inalterata, fino all'epoca moderna.
A questo scopo bisogna dotarsi di un cifrario dinamico: ogni lettera del testo in chiaro viene cifrata in maniera diversa di volta in volta, a seconda della sua posizione nel testo stesso. L'Alberti, da abile costruttore qual era, aveva anche ideato un pratico meccanismo, dotato di due copie dell'alfabeto su due dischi in grado di ruotare l'uno rispetto all'altro e quindi di entrare fra di loro in corrispondenza in tutta una molteplicità di modi: dopo aver cifrato una lettera del messaggio, una semplice rotazione di una o più tacche permette di cambiare la corrispondenza per la prossima lettera da cifrare. Per il suo uso da parte di chi riceve il messaggio è sufficiente conoscere il punto iniziale di corrispondenza dei dischi ed il numero di tacche di cui ruotare, dopo ogni operazione di cifratura. Questa è la chiave del sistema cifrante ideato da Leon Battista Alberti. Questa idea di una corrispondenza dinamica fra gli alfabeti, variabile nel corso del messaggio, fu portata a compimento ed utilizzata dal diplomatico francese Blaise de Vigenère (1523-1596) nel secolo successivo e diffusa nella sua opera Traité des chiffres ou secrètes maniéres d'escrire del 1586: i cifrari che ne conseguirono, rimasti in funzione praticamente fino al `900, presero tutti il suo nome: cifrari di Vigenère.
In questi cifrari, la corrispondenza dinamica si unisce all'uso di una parola convenzionale da usare come chiave che non occorre più scegliere senza ripetizioni la cui prima formalizzazione sembra essere presente nel trattato De furtivis literarum notis, vulgo de ziferis, scritto nel 1563 dallo scienziato e filosofo Giovan Battista della Porta.

L'idea è quella di utilizzare le lettere della parola chiave, ripetuta con continuità finché occorre in corrispondenza del testo in chiaro, per indicare il cifrario (del tipo Cesare) da usare in quel momento. In sostanza, la lettera da cifrare e la corrispondente lettera della parola chiave sono usate come una sorta di coordinate piane con cui individuare la lettera cifrata all'interno di un quadro -un tableau, come si dice oggi in Matematica- che contiene tutti i possibili cifrari di Cesare.
Ad esempio, si scelga ancora la parola salve come chiave e si supponga di voler trasmettere il messaggio:

studiate la matematica e sarete sempre contenti.

Le operazioni sono le seguenti:
1. ogni lettera del messaggio in chiaro viene messa in corrispondenza con una lettera della chiave, ripetuta quanto basta in corrispondenza delle sue lettere:

s t u d i a t e l a m a t e m a t i c a
s a l v e s a l v e s a l v e s a l v e

e s a r e t e s e m p r e c o n t e n t i
s a l v e s a l v e s a l v e s a l v e s

2. la lettera della chiave indica quale cifrario utilizzare per la corrispondente lettera in chiaro, con riferimento al seguente quadro, che contiene in maniera ordinata tutti i cifrari di Cesare:

3. per cifrare il messaggio si usano le lettere della parola chiave per individuare il cifrario: così, per la prima lettera s, si usa la riga che comincia con la s stessa di salve e si individua la n; per la successiva lettera in chiaro t il cifrario è quello che comincia con la a di salve e quindi rimane t anche dopo la cifratura; ora si ricorre alla l della parola chiave per cifrare la u, trasformandola in g e così via. Il messaggio cifrato prende forma...

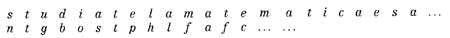
Continuate voi. Per apprezzare meglio l'uso del cifrario dinamico, si osservi come già da questo piccolo frammento risulta che la lettera e viene cifrata una prima volta con la p e la volta seguente con la c. Viceversa, la lettera f sta sia per la m che per la t grazie al fatto che queste lettere occupano posizioni diverse nel messaggio in chiaro.
È ovvio che, variando la parola chiave, si ottiene in questo modo una quantità infinita di cifrari. E se la chiave è abbastanza lunga - e non occorre più il vincolo che non abbia lettere ripetute - il periodo del sistema cifrante è lungo di conseguenza. Eppure non bisogna sottovalutare i metodi della Statistica né la capacità e l'ostinazione dei decrittatori: pur di conoscere un numero abbastanza alto di messaggi cifrati, nel corso del tempo sono stati elaborati dei metodi per trovare il periodo del sistema cifrante e da qui, in maniera empirica, risalire alla chiave.
Questi risultati, inutile dirlo, sono stati ottenuti in ambito militare. Gli artefici principali sono stati l'ufficiale prussiano Friedrich Wilhelm Kasicki (1805-1881) e, più tardi, il generale americano William Frederick Friedman (1891-1969). L'idea adottata da Kasiski si basa sull'analisi delle ripetizioni di gruppi di lettere, che sono poste in relazione diretta con la lunghezza della parola chiave: questo permette di scindere il cifrario nelle sue componenti monoalfabetiche, più semplici da decrittare. II lavoro di Friedman si concentra invece sulla probabilità che due lettere qualsiasi di un testo cifrato corrispondano in realtà alla stessa lettera in chiaro. Una breve esposizione di questi metodi, senza troppe complicazioni tecniche, si può trovare nell'agile testo di Berardi e Beutelspacher [2]. Siamo così giunti agli albori del `900, quando i dispositivi elettromeccanici sono pronti per l'elaborazione delle sempre maggiori quantità di dati che risultano connesse con l'operazione di decrittazione e, come riflesso, per la duale operazione di messa a punto del sistema cifrante.

LE MACCHINE CIFRANTI

Il periodo dei dispositivi per cifrare e decifrare vede dapprima sistemi meccanici, poi elettrici ed elettronici come conseguenza dell'evoluzione del concetto stesso di comunicazione. L'articolo [5] di Shannon del 1949 segna il definitivo ingresso della Crittografia nel campo della Teoria dell'informazione. È il periodo della Crittografia automatica.
Si è già detto della macchina cifrante Enigma, un complesso ideato per scopi commerciali già negli anni `20 e poi adattato, come standard delle comunicazioni riservate, dal comando tedesco nel corso della II guerra mondiale.
La macchina si componeva di un certo numero di dischi rotanti (tre nelle versioni più complesse), ciascuno dei quali realizzava una cifratura dell'alfabeto per mezzo di intricati circuiti elettrici. Inoltre questi rotori, per maggior complessità, venivano combinati e collegati fra di loro in maniera di giorno in giorno diversa, secondo una chiave anch'essa trasmessa in maniera cifrata; dopo ogni lettera trasmessa, subivano una rotazione.

Per la decrittazione risultarono utili un complesso di metodi, compresi quelli che si ottengono carpendo informazioni con lo spionaggio tradizionale ma anche statistiche, studio di strutture algebriche e combinatorie, esame delle abitudini dei trasmettitori tedeschi e delle espressioni gergali, analisi di grandi quantità di dati per mezzo di altre macchine elettromeccaniche appositamente costruite (le famose bombe, cosiddette per il loro classico ticchettio). Per maggiore comodità di operazione ed evidente economia di mezzi, Enigma usava un riflettore, grazie al quale la stessa chiave, e le medesime operazioni, venivano usate sia per cifrare che per decifrare: si batte sulla tastiera il testo in chiaro e, opportunamente disposta la macchina secondo la chiave, si legge su un visore il testo in codice; viceversa, se si batte il testo in codice, si legge direttamente il testo in chiaro. Il sistema crittografico è reversibile e questo carattere strutturale fornirà elementi fondamentali per la decrittazione.
L'affascinante storia di questa macchina, dei suoi principi costruttivi e di come un gruppo di matematici, filologi, enigmisti raccolti dal comando inglese a Bletchey Park sia riuscita a decrittarla, almeno in alcuni dei suoi aspetti, in particolare per la guerra sul mare, sono ben raccontate nella biografia di Alan Turing scritta da Andrew Hodges t6] e nella storia della Crittografia di Singh [3].
Altre macchine ed altri sistemi fanno parte della storia della Crittografia del `900. Il sistema più noto, e che ha resistito per il maggior periodo di tempo agli assalti della decrittazione, è quello fissato in maniera ufficiale nel 1977 dall'amministrazione degli Stati Uniti, il DES (Data Encryption Standard), un cifrario monoalfabetico la cui sicurezza, che riposava su una chiave da 56 bit (di cui 8 di controllo), è stata infranta nel 1998. Questo è il primo sistema di Crittografia commerciale, che viene stabilito come standard da un ente normativo, allo scopo di evitare il proliferare di sistemi cifranti incompatibili fra di loro.

Il DES esegue una serie di trasformazioni elementari ripetute più volte su pacchetti opportunamente strutturati del testo, in modo di sottoporre i bit che lo compongono ad una modifica globale, dipendente in maniera essenziale dalla chiave scelta: gli algoritmi sono resi pubblici; la chiave -nel rispetto più rigoroso del principio di Kerckhoffs- è l'unico dato fissato dall'utente.

L'aspetto importante è che la cifratura può avvenire in tempo reale con un calcolatore di media potenza. Inoltre il sistema è simmetrico nel senso che, come tutti i sistemi esemplificati fino a questo punto, la chiave viene usata direttamente per la decrittazione.
Un numero di 56 bit contiene una grande quantità di informazione: si hanno 7, 2 x 10¹⁶ chiavi diverse. Eppure, fin dal suo primo apparire, ai ricercatori apparve troppo corta per affrontare le risorse che prevedibilmente si sarebbero sviluppate nel futuro. E, come previsto, questa fu la causa principale della sua decrittazione, anche se a questo scopo fu necessaria la forza di migliaia di computers che lavoravano simultaneamente, coordinati via Internet.
in effetti, è nel contesto delle grandi macchine da calcolo dedicate ai problemi della Crittografia che nel `900 sorge la coscienza che, per avere un cifrario perfetto, vale a dire un cifrario che non possa essere infranto, la chiave deve possedere tanta informazione quanto quella dei possibili messaggi. Un apparente paradosso, che tuttavia serve solo a spostare in avanti la nozione stessa di chiave crittografica. Tale è ad esempio il cifrario di Vernam, che prende il nome dall'ingegnere delle telecomunicazioni Gilbert Vernam (1890-1960) in cui la chiave è un generatore di numeri casuali. Non sorprende che una chiave qualsiasi si possa codificare in termini numerici: è chiaro che, con questo livello di sviluppo e l'insorgenza dei metodi digitali, si può ben pensare che anche il messaggio non sia che un numero, codificato in un certo numero di bit. Il vero problema che rimane è quello della chiave: della sua generazione, della conservazione e della trasmissione.
In questo modo, generata ad ogni nuova utilizzazione, la chiave è sempre nuova; non si ripete mai da una trasmissione all'altra e, anzi, viene eliminata dopo l'uso (gli americani parlano di one-time pad, per sottolineare l'uso non ripetibile della chiave) ma il vero segreto è ormai concentrato sulla maniera con cui viene generata.

aV(aVb)=b

garantisce la reversibilità del sistema.
Ma non occorre necessariamente un ambiente tecnologico di grande sofisticazione per mostrare il senso dell'uso di una chiave one-time pad: pensate, ad esempio, di fissare con il vostro interlocutore che la chiave per trasmettere messaggi cifrati sia data da una certa edizione della Divina Commedia. Voi eseguite la cifratura à la Vigenère usando come chiave tutte le lettere consecutive dell'opera di Dante: "nelmezzodelcammindinostravita......" con la convenzione che per il prossimo messaggio la chiave parte da dove si è arrestata nel precedente. Evidentemente, il sistema non ha alcun periodo: la cifratura non si ripete mai allo stesso modo; eppure una macchina che procedesse per tentativi sarebbe senz'altro in grado di decrittare prima o poi i vostri messaggi e magari riscrivere in bella tutti i versi della Divina Commedia!
A questo punto dello sviluppo, occorre un idea che fornisca alla nozione di chiave crittografica una enorme quantità di possibilità e allo stesso tempo la liberi dalla necessità di essere condivisa fra più soggetti, perfino fra chi trasmette e chi riceve. La gestione delle chiavi, spesso ingombranti, la loro generazione, il loro invio ai destinatari, le esigenze di sicurezza ... questo è l'autentico punto critico dei sistemi cifranti. E questo è ciò che ha ricevuto un forte miglioramento dall'idea di chiave pubblica, come opposta all'uso privato, personale, segreto della chiave. Una chiave che potete comunicare a tutti quelli che vogliono cifrare un messaggio e mandarvelo, ma che non è utile per la decifrazione che solo voi sapete eseguire.

LO SCAMBIO DELLA CHIAVE

Riprendiamo Alice e Bob alle prese con il problema di scambiarsi una chiave da usare per le loro comunicazioni personali, al riparo dalla curiosità di Charlie. Non hanno la possibilità di incontrarsi ma dispongono di macchine con una buona capacità di calcolo e di comunicazione, pur sapendo che le loro e-mail sono regolarmente intercettate. Procederanno in questo modo: per telefono -anch'esso intercettato dall'invidioso Charlie- fissano un numero intero positivo n; poi ciascuno di loro ne sceglie per proprio conto un altro, senza rivelarlo a nessuno: Alice fissa a e Bob fissa b, Alice comunica a Bob il valore di n^a e Bob le comunica il valore di n^b (e Charlie ascolta tutto). Ora Alice calcola n^ab semplicemente elevando al suo esponente segreto a il valore che Bob le ha comunicato e analogamente Bob calcola lo stesso valore elevando na all'esponente b che solo lui conosce. Tutto qui (nella proprietà commutativa del prodotto):

(n^a)^b = (n^b)^a = n^ab

ed entrambi conoscono questo numero, che servirà loro da chiave crittografica. Il deluso Charlie conosce separatamente n^a ed n^b ma non a e b, per i quali dovrebbe calcolare due logaritmi in base n. Questo è il suo problema, perché Alice e Bob hanno scelto dei numeri (n, a e b) abbastanza alti per mettere i sistemi di calcolo di Charlie al di fuori da questa possibilità, semplice in linea di principio ma disperatamente lungo nella pratica.
Si capisce dove sta il punto: il calcolo degli esponenziali, con un sistema anche poco o potente, si può fare facilmente mentre il suo inverso, il logaritmo, può richiedere risorse di calcolo intollerabili in termini di tempo.

Questa è l'idea che è sorta negli anni `70 ed è stata poi pubblicata in Diffie e Hellman [7]: dotarsi di una funzione - invertibile sì, altrimenti non è possibile decifrare, ma facile da calcolare in un senso e molto difficile, lunga o praticamente impossibile da calcolare in senso inverso - una funzione che con la terminologia anglosassone ormai in voga viene detta trapdoor, a trabocchetto.

È facile cadere, mentre risalire risulta praticamente impossibile (a meno che non si conosca una via segreta).

Una di queste funzioni, di fatto quella che viene usata nelle più diffuse implementazioni dei sistemi crittografici, è data dal prodotto di numeri interi: mentre questa è un'operazione facile da eseguire anche fra numeri con molte cifre (pur di disporre di strumenti di calcolo abbastanza potenti), l'operazione inversa che è quella di scomposizione in fattori può risultare intollerabilmente lunga. Le stime relative alla fattorizzazione di un numero di qualche centinaio di cifre decimali, pur avendo a disposizione i più moderni sistemi di calcolo veloce, si misurano ancora in termini di milioni di anni. Si tratta di un problema di Teoria dei numeri che sembra computazionalmente intrattabile.

LA CHIAVE PUBBLICA

La prima applicazione al problema della trasmissione cifrata dei messaggi, cioè al problema principale della Crittografia, si basa sull'osservazione -banale ma decisiva- che la chiave cifrante rende simmetrico il canale di comunicazione. Da A si trasmette a B, ma si potrebbe anche invertire il processo senza alterare né il cifrario, né la chiave: eventualmente, se il cifrario non è reversibile, occorre invertire tutte le operazioni.

La simmetria del canale -questa componente strutturale del processo di comunicazione- viene alterata nella pratica con una funzione cifrante a trabocchetto: il canale viene reso asimmetrico; permette la cifratura solo in una direzione e lo stesso trasmettitore -che possiede le istruzioni per cifrare- non è tuttavia in grado di decifrare i messaggi.
Ci sono ora due chiavi distinte: una per cifrare, nota pubblicamente a tutti quelli che vogliono mandare un messaggio cifrato, ed una per decifrare, rigorosamente tenuta segreta dal destinatario dei messaggi. Ovviamente, le chiavi sono fra di loro dipendenti - altrimenti non si potrebbero mai decifrare i messaggi - ma la conoscenza di una non è sufficiente a far risalire all'altra ... a meno che non si conosca qualche segreto: una funzione a trabocchetto.
Il problema della condivisione della chiave crittografica è completamente risolto e la semplicità della cifratura viene connessa ad una estrema difficoltà della decifratura. Tutto dipende dalla funzione a trabocchetto!

IL SISTEMA RSA

Questo sistema, di pochi anni successivo all'idea delle funzioni a trabocchetto, compare in Rivest, Shamir e Adleman [8] e si basa proprio sulla difficoltà a reperire sufficienti risorse di calcolo per la scomposizione in fattori primi di numeri interi che hanno molte cifre.

L'algoritmo proposto per l'implementazione pratica sfrutta in maniera sapiente la complessità computazionale di alcuni processi della Teoria dei numeri, relativi alla Aritmetica modulare (di cui si parla nel box qui accanto, nel quale si illustrano anche i risultati che permettono all'algoritmo di funzionare).
Vale la pena di osservare che questi risultati, tutti riassunti e compiutamente espressi nelle Disquisitiones Arithmeticae di Gauss (1801), erano sostanzialmente già noti ad Eulero e, in qualche caso, anche a Fermat nel corso del `600. A noi sembra che l'applicazione di questi risultati, trovati in un periodo in cui le prospettive del calcolo veloce non erano neppure lontanamente concepibili, sia un esempio straordinario della fecondità del pensiero matematico e della razionalità che è intrinseca alla ricerca di questi grandi personaggi della Matematica.
Cominciamo ad illustrare l'idea che si trova alla base del sistema di Crittografia a chiave pubblica, osservando che alcune operazioni che possono sembrare a prima vista molto onerose rispetto al tempo di calcolo risultano invece facilmente calcolabili: è questo il caso, ad esempio, degli esponenziali e del massimo comune divisore di due numeri -anche molto grandi- così come del calcolo dei resti modulo n. È interessante notare che questa semplicità, pur nelle varianti che sono state elaborate nel tempo, è essenzialmente fornita da un altro risultato classico di grande importanza: l'algoritmo delle divisioni successive o algoritmo euclideo, che affonda le sue radici e la sua ragione d'essere negli Elementi di Euclide e nei problemi dibattuti nel III secolo prima di Cristo (per i problemi di complessità computazionale che riguardano le diverse operazioni si può consultare, ad esempio, Salomaa [9] oppure Ferragine e Luccio [10]).

Tutto è pronto per mettere in funzione il sistema: chi intende divenire il destinatario di messaggi riservati - diciamo che sia Bob - fissa e rende pubblica la propria chiave, in modo che chiunque voglia mandargli un messaggio cifrato (non solo Alice, ma anche altri) sappia come comportarsi. A questo scopo, Bob deve compiere alcune scelte ed alcune operazioni preliminari: è superfluo osservare che dalla bontà di queste scelte dipende la sicurezza del cifrario.

Qui non vale però la pena di entrare in questi dettagli, ma piuttosto cercare di chiarire il metodo nei suoi principi (chi sia invece impaziente di conoscere questi particolari consulterà Koeblitz [11], Salomaa [9] o Ferragine e Luccio [10]).
Bob sceglie una coppia di numeri (e, n) con la condizione che e e φ(n) non abbiano fattori primi comuni:
MCD(e, φ(n)) = 1
Abbiamo detto che questa scelta non presenta difficoltà di calcolo anche se i due numeri e ed n saranno piuttosto grandi e, come è stato osservato, è bene che la scelta rispetti opportuni criteri per aumentare la solidità del sistema. Questa coppia (e, n) è la chiave pubblica di Bob, che lui lascia a disposizione di tutti, ma attenzione... Bob non farà nessun accenno al valore di φ(n) -neppure ad Alice- perché questo è il suo segreto, la sua chiave personale che permette di decifrare i messaggi.
Per la verità, per mezzo di φ(n), Bob calcola un numero d che risolva la congruenza di primo grado:

e*x≡1 (mod φ(n))

È questo numero d (mod φ(n)) che utilizza direttamente per decrittare i messaggi. La condizione che e e φ(n) siano primi fra di loro garantisce che la congruenza precedente ammette un'unica soluzione, a meno di congruenze modulo φ(n).
Ora chiunque ha la possibilità di mandare a Bob un messaggio riservato e questi è pronto per decrittarlo. Il procedimento avverrà così: Alice, ad esempio, gli vuole comunicare il messaggio m (che è già opportunamente codificato con un numero). A questo scopo, eleva m all'esponente e e calcola il resto modulo n del numero ottenuto. Ha utilizzato esattamente l'informazione che Bob ha comunicato a tutti - la sua chiave pubblica (e, n) - ottenendo il messaggio cifrato c:

c≡m^e (mod n)

Come può Bob ricostruire il messaggio, cioè risalire da c ad m, e perché nessun altro che intercetti c e conosca la chiave pubblica di Bob è in grado di fare altrettanto? Per Bob è facile, perché conosce φ(n) ed ha calcolato d. Gli basta elevare il messaggio cifrato c all'esponente segreto d. Infatti, per come è stato trovato, ed = kφ(n)+1 in corrispondenza a qualche intero k e si ha quindi:

c^d≡(m^e)^d ≡m^ed≡m^kφ(n)+1≡(m^φ(n))^k*m ≡m(mod n)

dove si sono usati la proprietà di stabilità della relazione di congruenza rispetto al prodotto ed il teorema di Eulero-Fermat: m^φ(n)≡1 (mod n).
Qual è il segreto che permette solo a Bob di decifrare il messaggio? Chiaramente risiede nell'esponente d che usa e che inverte (modulo φ(n)) la chiave cifrante e. E d si ricava conoscendo φ(n): come si è detto, è qui il vero segreto perché il calcolo di φ(n) è tanto complesso quanto la scomposizione di n in fattori. Quando ha scelto la propria chiave pubblica, Bob ha avuto l'accortezza di scegliere n come prodotto di certi numeri primi e dunque, grazie alla proprietà moltiplicativa della φ di Eulero, il calcolo di φ(n) gli risulta estremamente agevole. Si saranno riconosciute, in questo processo, le proprietà fondamentali del calcolo modulare e della φ di Eulero.
La strategia ottimale di Bob è precisamente quella di scegliere n come prodotto di due soli numeri primi, abbastanza grandi e non troppo prossimi fra di loro. In questo modo è n = p*q con p e q primi e si ha:

φ(n)=(p - 1)*(q - 1)

Dunque, tutto si basa sulla scomposizione in fattori primi. Questo fatto indica anche il "punto debole" del sistema crittografico: la sicurezza riposa sulla nostra "ignoranza" di molti fenomeni relativi ai numeri primi. Se e quando la ricerca matematica riuscirà a risolvere i problemi della distribuzione dei numeri primi e troverà un metodo efficiente per la scomposizione in fattori, il metodo perderà immediatamente la sua efficacia... e ci si dovrà rivolgere verso nuove funzioni a trabocchetto.
Ancora una volta, come spesso accade, il progresso tecnico rimane subordinato in maniera diretta alla conoscenza teorica.

LA FIRMA DIGITALE

Il problema della autencità del mittente sta diventando sempre più importante giacché si operano sempre più operazioni, di varia natura e varia importanza, per via telematica. La firma digitale sta diventando uno strumento legale in numerosi Paesi.
Qual è il suo principio? Di fatto si realizza "invertendo" il principio della trasmissione cifrata con chiave pubblica. Dunque, supponiamo che Bob -sempre lui- voglia comunicare il messaggio m a qualcuno ma che, questa volta, l'aspetto importante non risieda nella segretezza di m -che vengano pure a saperlo tutti!- bensì nel farsi riconoscere con sicurezza dal destinatario. Questa è in fondo la funzione assolta dalla nostra firma: solo noi la possiamo fare e di conseguenza tutti sono in grado di riconoscere che un dato documento proviene da noi.
Ad esempio, Bob sta scrivendo per posta elettronica dall'estero alla propria banca per farsi accreditare una qualche cifra: il riconoscimento deve essere sicuro. Naturalmente Bob ha la propria chiave pubblica (e, n), che tutti conoscono e per conto proprio ha anche calcolato l'esponente d che gli permette di decrittare i messaggi. Forte di questi dati, Bob invia alla propria banca come messaggio la coppia (m, m^d) e viene riconosciuto con sicurezza perché, con un calcolo analogo a quello appena fatto, si verifica subito che:

m≡(m^d)^e (mod n)

In altri termini, chi ha mandato il messaggio cifrato m^d dichiarando che in chiaro è il messaggio m, non può che essere Bob.
Si osservino due fatti: dapprima, che Bob non firma semplicemente dichiarando il proprio esponente d, che non deve rivelare e che per altro non sarebbe sufficiente a farlo riconoscere. E poi, come conseguenza di questo primo fatto, non esiste una "firma" disgiunta dai documenti, depositata da qualche parte e riconosciuta per confronto quando è necessario: ogni firma è contestuale ad un documento, vive con esso e solo con esso.
Anche se Bob non ha scelto una propria chiave pubblica, qualcuno può farlo per lui. Supponiamo ad esempio che sia cliente di un Istituto di credito che lo deve riconoscere quando preleva dei soldi da un distributore automatico. È chiaro che l'Istituto dovrà dotare Bob, e tutti gli altri clienti, di una tessera con i propri dati magnetizzati e fornirà loro un codice personale che permetta facilmente il riconoscimento. Ma, d'altro lato, è altrettanto chiaro quanto sia rischioso tenere le informazioni relative ai clienti ed ai loro codici personali da qualche parte, ad esempio in un data base sulla cui sicurezza si dovrebbe sorvegliare incessantemente.
Il sistema della firma digitale consente all'Istituto di calcolare per ciascun cliente una sua chiave pubblica (e, n), calcolare il coefficiente speciale d, comunicarlo all'interessato - non importa fargli sapere la chiave (e, n) - e poi... cancellare d dai propri schedari. È possibile ugualmente effettuare il riconoscimento, solo usando (e, n), che può anche essere lasciato in bella mostra, a disposizione di tutti.
La segretezza del sistema coincide con la segretezza di d, che solo l'interessato conosce: questo futuro di codici segreti, chiavi pubbliche e calcolo sembra aspettare tutti noi.

IL SORTEGGIO DI ALICE E BOB

Rimane da esaminare la maniera con cui due contendenti possono eseguire una estrazione a sorte, senza avere la possibilità di incontrarsi per controllare che tutte le operazioni si svolgano correttamente. Questo problema non riguarda direttamente i procedimenti della Crittografia - trasmissione e validazione di messaggi riservati - ma si basa sullo stesso principio della chiave pubblica, vale a dire sulla possibilità di eseguire un'operazione la cui inversa non è accessibile al calcolo immediato, a meno di avere qualche informazione supplementare.
In questo caso, Alice e Bob di comune accordo sceglieranno una funzione a trabocchetto f. Quindi Alice, ad esempio, fissa un valore x dell'argomento, calcola f (x) e propone a Bob di scegliere a caso una proprietà di x che abbia il 50% di probabilità di essere vera: ad esempio, quando x è un numero intero, gli chiede di dire se è pari o dispari. È chiaro che per Bob risulta impossibile risalire da f (x) ad x: se indovina, la vittoria del sorteggio è sua, altrimenti è di Alice e lo stesso Bob può convincersene facilmente. La scelta è stata casuale ed equa, come si richiede ad un sorteggio.
A1 solito, anche per una procedura di questo tipo le funzioni più interessanti sono prese dalla Teoria dei numeri. Eccone una che sfrutta una proprietà non banale: come nella scelta della chiave pubblica, Alice fissa due numeri primi molto grandi p e q e calcola il loro prodotto n=p*q. Comunica a Bob il valore di n ma non la scomposizione in fattori che, al solito, è il suo segreto. Da parte sua, anche Bob esegue la scelta di un intero u compreso fra 1 ed n/2, calcola u² (mod n) e comunica questo numero ad Alice. Alice può facilmente risalire alle due radici quadrate di u² che sono comprese nell'intervallo (1,n/2) in quanto conosce la fattorizzazione di n e, se indovina il valore di u scelto da Bob, avrà la vittoria nel sorteggio: per questo ha esattamente il 50% di probabilità di vincere. Dunque Alice comunica la sua scelta a Bob, il quale non può che consentire nel caso Alice abbia indovinato, perché altrimenti gli viene chiesto di dire qual è l'altra radice quadrata di u²... ma lui non è in grado di calcolarla.

CONCLUSIONI

È ormai chiaro che la Crittografia - evolutasi grazie ad esigenze commerciali, diplomatiche e militari, ha abbandonato recentemente il mondo delle spie e dei generali (o meglio, ha esteso il proprio raggio d'azione) per coinvolgere operazioni che sono quotidianamente compiute da tutti in ambito privato e personale. In questo modo ha investito problemi di grande valore sociale e politico, ha rilevanza sul piano economico e del diritto, coinvolge la nostra privacy, la libertà d'espressione e la riservatezza delle nostre comunicazioni. Non è più solo un fatto "tecnico" che trova applicazione in un mondo importante, ma limitato e per altro estraneo alla nostra consapevolezza. La necessità di districare questo intreccio di applicazioni, distinguere il supporto tecnico dalla funzione, l'operatività dall'utilizzazione pratica e dalla sua valenza ideale, è un compito molto complesso perché la materia ha una evoluzione rapida, costantemente al passo con la diffusione dei metodi di calcolo veloce e di comunicazione digitale: su questo intreccio vale la pena di indicare al lettore italiano il volume di Giustozzi, Monti e Zimuel [4]. Dall'altro lato, l'estrema complessità delle problematiche coinvolte si riflette nel fatto che oggi la Crittografia si trova al crocevia pratico e concettuale di numerose discipline scientifiche: anche il solo problema di affrontare il puro fatto tecnico, indipendentemente dagli usi che se ne fanno, costringe a rivolgersi in maniera non banale alla teoria degli algoritmi e della complessità computazionale, con escursioni nel campo delle macchine calcolatrici e della teoria dell'informazione: una serie di materie estremamente moderne, che in qualche caso cercano ancora il loro assetto formale, con profonde e varie influenze l'una sull'altra, attraverso le quali viene amplificata l'ampiezza delle competenze necessarie.

Quanto alla Matematica, la Teoria dei numeri sembra oggi la materia che più si presta a reperire le funzioni a trabocchetto ed a trovare strategie algoritmiche complesse. Ma la Crittografia si rivolge anche ampiamente alle tecniche statistiche e a quelle del Calcolo delle probabilità, alle strutture algebriche e, recentemente, anche alla Geometria algebrica.

Come si vede, nella sua veste moderna di Crittografia a chiave pubblica, si tratta di un campo di ricerca di grande interesse teorico, direttamente collegato al valore delle applicazioni, anzi spesso dettato immediatamente dalle loro esigenze.
Ma vale anche la pena di osservare che fuso dei sistemi crittografici non è lasciato completamente libero. Per motivi di sicurezza, i programmi di crittografia destinati alle applicazioni civili sono soggetti a controllo e, con qualche risvolto comico, vengono equiparati alle "armi da guerra" allo scopo di vietarne l'esportazione: tale è la storia vera affrontata da Phil Zimmerman, autore del software PGP (Pretty Good Privacy) e convinto assertore del diritto personale alla privacy, il cui programma non si può più scaricare liberamente dalla rete.
E così, in qualche modo, la crittografia viene "ricacciata" a forza nell'ambito dei problemi militari, coperti da segreto.