La disfida algebrica
Chiunque abbia frequentato il biennio di un qualsiasi Istituto superiore, ha familiarità con la formula risolutiva per radicali, delle equazioni algebriche di 2° grado. L'equazione ax2+bx+c=0 ammette, come soluzioni:
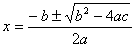
con varie discussioni a seconda che Δ=b2-4ac sia positivo, nullo o negativo. Pochi sono a conoscenza, tuttavia, dell'esistenza di una formula risolutiva generale (per radicali) delle equazioni di 3° e 4° grado! Quei pochi che ne sono a conoscenza ignorano, per lo più, la vera e propria saga che ha portato alla loro scoperta, da parte di un manipolo di algebristi italiani, in pieno Rinascimento.
Alzi la mano chi non ha mai sentito il nome di Tartaglia, assurto agli onori delle cronache matematiche come padre dell'omonimo triangolo (noto ai francesi come triangolo di Pascal e agli inglesi come triangolo di Newton, partorito in realtà dalla mente del cartografo tedesco Peter von Bienewitz...).
Partendo dal presupposto che siate stati in molti ad alzare la mano, corre l'obbligo di ricordare chi fosse Niccolò Fontana detto il Tartaglia, proprio prendendo le mosse da questo suo buffo soprannome.
II Fontana, infatti, nacque a Brescia intorno al 1499 ed era dunque un ragazzino durante il sacco di Brescia del 1512 ad opera delle truppe francesi. Gettatosi davanti alla spada di un bravaccio, per difendere il fratellino, il povero Niccolò fu colpito in pieno viso, riportando danni gravissimi al volto e restando balbuziente per tutta la vita: da qui il soprannome di Tartaglia.
Le vicende belliche e le successive traversie della vita, oltre a fare del matematico bresciano un uomo assai poco fortunato, debbono aver contribuito non poco a renderlo un carattere irascibile e malinconico, poco adatto alla vita di società. Questo non gli impedì, tuttavia, di acquistare rapida fama di bravo matematico e di divenire lettore presso il prestigioso Studio di Bologna ovvero docente dell'Università di Bologna, dove inizia la nostra storia.
AI tempo di Tartaglia, l'Algebra era poco più evoluta di quella conosciuta dai babilonesi e tenuta in scarsissima considerazione dai matematici, per i quali la Matematica - con la m maiuscola - era sopra ogni cosa la Geometria. II lettore moderno rimarrebbe sicuramente sconcertato leggendo un trattato di Algebra tardo medievale e rinascimentale, non fosse altro per la totale mancanza della simbologia a noi nota. II Cardano - di cui avremo modo di parlare più avanti - scrive "Il cubo e sei volte il lato siano uguali a 20" al posto del nostro x3+6x=20, decisamente più sintetico! È facile pensare quanto potesse essere complicato scrivere una delle micidiali espressioni tanto care ai nostri libri di testo. A titolo di esempio, ricordiamo che il grande algebrista tedesco Michael Stiefel usava le abbreviazioni delle parole tedesche coss, zensus, cubus, zenzisensus per indicare le potenze successive dell'incognita x, x2, x3, x4.
II Rinascimento italiano coincise con la rinascita dell'Algebra e, in particolare, con un rinnovalo interesse per la ricerca di una formula risolutiva generale per le equazioni algebriche di 3° e 4° grado. Intorno a questo problema iniziarono ad arrovellarsi gli ingegni più insigni dell'epoca, i quali presero (come era costume) a sfidarsi in pubbliche gare. I matematici, infatti, erano soliti custodire gelosamente le proprie scoperte per poter sfidare altri colleghi, attraverso cartelli di matematica disfida. La sfida consisteva nel risolvere un problema e nel trovare metodi migliori e più rapidi dei propri, certi della possibilità di far fare una figuraccia al rivale, eliminando così un concorrente nella eterna caccia di un mecenate.
L'eroe buono della nostra vicenda è Scipione dal Ferro (1465-1526), "vecchio bolognese'; professore presso l'Ateneo di Bologna. In circostanze e tempi mai chiariti, aveva scoperto la formula risolutiva (vedi [POESIA MATEMATICA]) dell'equazioni di 3° grado, ma senza mai pubblicare nulla e confidando il segreto solo in punto di morte a un mediocre allievo.
Questi, ancora incredulo per la fortuna capitatagli, nel 1535 si precipitò a sfidare pubblicamente il grande Tartaglia, che era giunto alla stessa formula risolutiva di Scipione dal Ferro con metodi, però, indipendenti. Ciascuno dei due contendenti propose all'altro 30 problemi da risolvere entro un tempo stabilito. II giorno fatidico giunse e... il trionfo del bresciano fu pieno e senza possibilità di dubbi! Aveva risolto tutti i quesiti proposti dall'altro contendente, mentre questi non era riuscito a venire a capo di nessuno dei problemi proposti da Tartaglia.
A questo punto della vicenda entra in scena il black hero della situazione, [GEROLAMO CARDANO] da Pavia. Fu un tipico figlio del Rinascimento, con un piede nella modernità e l'altro nel medioevo, molto scienziato e un poco stregone, afflitto da una famiglia di figli disgraziati, uno dei quali condannato come delinquente abituale e l'altro, avvelenatore della matrigna, condannato a morte e decapitato (per tacere del segretario di Cardano, Ludovico Ferrari, probabilmente avvelenato dalla sorella!). Malgrado la dubbia fama del personaggio, il povero Tartaglia ritenne di poterne fare il proprio confidente e di potergli comunicare, in tutta sicurezza, il segreto- sino ad allora gelosamente custodito -della formula risolutiva delle equazioni di 3° grado. Quando le voci dell'esistenza di tale formula iniziarono a circolare in Bologna, Cardano si ritenne liberato da ogni vincolo di segretezza e pubblicò la formula risolutiva per le equazioni di 3° e 4° grado nella sua celebre opera Ars Magna, che fece di lui il più celebre algebrista d'Europa.
È inutile dire quali furono i sentimenti del Tartaglia, ferito nell'orgoglio e scavalcato dal luciferino medico pavese il quale comunque, a dire il vero, non mancò mai di sottolineare l'originalità del contributo dato dai colleghi alla scoperta delle formule risolutive. Basti ricordare cheTartaglia accusava Cardano di essere "molto più tonto di quello che io istimava". Le litigate tra i due diverranno leggendarie e si placheranno solo con la morte dei contendenti.
I successi del terzetto - Ferro, Tartaglia e Cardano - spingeranno i matematici a ricercare - per i due secoli (e mezzo) successivi - la formula risolutiva delle equazioni algebriche di quinto grado, dando origine a un'altra avvincente saga che troverà la sua conclusione con l'irruzione sulla scena matematica di altri personaggi straordinari e con un risultato sorprendente.
Ma questa è un'altra storia...
L'ALGEBRA DEI BARBIERI La parola Algebra viene dall'arabo al-jabr che, tradotto in latino, diventa restauratio ovvero ristabilimento dell'equilibrio (di un'equazione quando si porta un termine da un membro all'altro, appunto cambiando segno). In Spagna, durante la dominazione araba, quasi tutte le botteghe di barbiere –nella loro insegna- recavano la scritta al-jabr. Non è che i barbieri fossero tutti laureati in Matematica (e in Algebra). Il motivo era, ovviamente, un altro. In Spagna, in quel periodo, i barbieri fornivano anche le prime prestazioni medico-infermieristiche. Si occupavano quindi della restauratio, ma del corpo umano … In altre parole, facevano anche gli aggiusta –ossa. Da qui, la loro insegna … algebrica. |
LA FORMULA RISOLUTIVA
Per equazione algebrica, si intende un'equazione in cui intervengono solo polinomi. Tutte le equazioni che non sono tali si definiscono trascendenti.
Per formula risolutiva generale (per radicali) si intende una formula risolutiva contenente solo le quattro operazioni fondamentali e l'estrazione di radice di indice qualsiasi. Si può dimostrare che qualsiasi equazione algebrica, completa, di 3° grado è riconducibile ad un'equazione del tipo x3+px=q (in cui manca il termine di secondo grado) La formula matematica di Cardano (in riferimento a quest'ultima equazione) diventa:
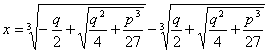
la quale diventa fornisce un'unica soluzione reale dell'equazione nel caso in cui è
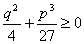
Cardano non esitò a definire sofistiche le radici quadrate di numeri negativi e a giudicare un tale studio “tanto sottile, quanto inutile”. L'analisi di tale caso iniziata già nel ‘500 con un altro matematico bolognese, Raffaele Bombelli, porterà invece all'introduzione, niente meno, dei numeri complessi. Dare significato all'operazione di radice quadrata, anche quando il radicando è negativo, è un'esigenza che si può porre già all'interno del campo reale.
All'esterno del Duomo vecchio di Brescia (noto come la Rotonda per la caratteristica forma circolare) c'è una targa che racconta questa storia. II 12 febbraio 1512, Gastone di Foix (grande capitano nella campagna d'Italia) entrò in Brescia in aiuto dei francesi, che erano stati scacciati dai bresciani, e lanciò i suoi uomini al saccheggio. Tra la folla impaurita che scappava per le strade, vi era anche un fanciullo di nome Niccolò, che cercò riparo e salvezza nel Duomo vecchio. II piccolo, nella fuga, venne colpito "anche alle labbra"; ma riuscì a salvarsi. II suo nome era Niccolò Fontana e divenne un grande matematico ma, poiché la ferita al labbro l'aveva reso balbuziente, venne chiamato Niccolò Tartaglia.
