La Geometria degli origami
La forza degli origami
di Liz Newton (traduzione a cura di Marco Crespi)
versione originale su Plus Magazine.
A nove anni ero bravissima con gli origami. Avevo un amica, Kim, che era in visita in Inghilterra dal Giappone. Doveva starci un anno. Mentre le mostravo alcune delle attività simpatiche da fare nel mio Paese, lei mi insegnò molte attività tipiche giapponesi: dal disegno dei cartoni Manga alla preparazione del sushi. Ovviamente, l’altra cosa di cui mi parlò furono gli origami e un pomeriggio mi spiegò come realizzare una gru di carta. Da quel momento, diventai la più grande maestra d’origami nel mondo. O così pensavo. Passarono altri 15 anno quando realizzai che non era proprio così. In realtà, niente in me era vicino a essere considerato “maestro d’origami”. |  |
| Sorprendentemente, non ero la sola ad aver fatto quell’errore. C’erano molti artisti in questa storia che, in buona fede, credevano di aver prodotto gli origami più belli e più complicati. In realtà fu solo all’inizio del ventesimo secolo, con la crescita dei computer, che gli origami presero il volo. | Scheletro di Allosauro realizzato da Robert J. Lang da 16 fogli quadrati (interi). Immagine gentilmente concessa da Robert J. Lang. |
Una breve storia degli origami
Sebbene gli origami siano tutt’oggi sinonimo di Giappone, la prima traccia di questa tradizione arriva dalla Cina, dove la carta venne prodotta fin dal 200 come alternativa economica alla seta. L’arte cinese del piegare la carta fu conosciuta come Zhezhi e fu portata con la carta in Giappone nel 6 secolo da monaci buddisti cinesi.

Pegaso realizzato da Robert J. Lang. Immagine gentilmente concessa da Robert J. Lang.
Gli origami iniziarono così a diffondersi in Giappone. La stessa parola giapponese “origami” è la composizione di due parole: “ori”, che significa piegare, e “gami” che significa carta. Questa arte fu per molti secoli (e lo è ancora) un popolare passatempo per i bambini giapponesi.
E questo sarebbe rimasto se non fosse stato per l’operaio giapponese Akira Yoshizawa. Nato nel 1911 da una famiglia di produttori di latte, Akira si appassionò agli origami da piccolo ma, come molti bambini, li abbandonò gradualmente crescendo e trovando nuove attività che occupavano il suo tempo. Tuttavia, a differenza degli altri bambini, riaccese la sua passione per gli origami subito dopo i vent’anni. Aveva iniziato a lavorare in una fabbrica, dove insegnava la Geometria ai giovani operai, e realizzò che gli origami potevano essere un modo semplice e efficace per insegnare ai suoi studenti i concetti di angolo, linea e forma.
Con la pratica, Yoshizawa sviluppò alcune tecniche pionieristiche come quella del “wet folding” (letteralmente piega bagnata) che permetteva schemi più complicati e la possibilità di realizzare su un singolo foglio un maggior numero di curve. Il suo lavoro fece partire il rinascimento degli origami Le sue nuove tecniche cambiarono gli origami da passatempo a forma d’arte.
Con il disegno di schemi sempre più complessi, questa arte iniziò ad attirare l’interesse dei matematici che avevano la stessa ideaa di Yoshizawa: c’era una grande intersezione tra l’arte di piegare la carta e la Geometria. Gli studi matematici degli origami finalmente portarono a un nuovo approccio a due problemi le cui radici, molti molti anni prima, risalivano a differenti culture e differenti continenti.
Gli elementi di Euclide
Euclide di Alessandria era un matematico greco che visse più di 2000 anni fa ed è spesso chiamato il padre della Geometria. Il libro di Euclide Gli elementi è il più famoso nella storia della Matematica ed è la prima discussione sistematica conosciuta della Geometria.
Euclide sapeva che, usando una riga (senza l’indicazione delle lunghezze) e un compasso, era possibile svolgere un gran numero di operazioni geometriche come disegnare un pentagono, un esagono e un cerchio. Ciò era largamente noto a quel tempo e il fatto che Euclide fosse in grado di farlo non è certo insolito.
Tuttavia, quel che Euclide fece e che nessun altro aveva fatto prima, fu l’utilizzo di un approccio sistematico alla Geometria. Ogni costruzione geometrica e ogni risultato matematico contenuti ne Gli elementi derivava passo dopo passo da un insieme di 5 assunzioni, che includevano le operazioni di base che era possibile fare con riga e compasso:
- dati due punti, si può disegnare una linea retta che passi per i due punti;
- ogni segmento può essere esteso indefinitamente;
- dato un punto e un segmento che parte da quel punto, è possibile descrivere un cerchio con il punto dato come centro e il segmento come raggio;
- tutti gli angoli retti sono uguali tra loro;
- data una retta e un punto P esterno alla retta data , c’è una e una sola altra retta che passa per P e che non incontra la retta originale.

Colibrì su un fiore realizzato da Robert J. Lang. Immagine gentilmente concessa da Robert J. Lang.
Queste assunzioni, note come assiomi di Euclide, sembrano ovvi e sicuramente Euclide stesso li considerò ovvi in quanto auto-evidenti. Ma la loro bellezza sta nel fatto che possono essere usati per costruire dimostrazioni geometriche di teoremi che sono immensamente più complessi degli assiomi stessi.
C’è però anche una serie di limitazioni alla Geometria euclidea. Due tra i più famosi problemi dell’antichità erano la trisezione dell’angolo (dividere un angolo in tre parti uguali) e la duplicazione del cubo (costruire un cubo che abbia esattamente un volume doppio del cubo iniziale). Nella leggenda, i cittadini dell’antica Delo si trovarono di fronte al secondo problema quando l’oracolo di Delfi chiese loro di raddoppiare il volume del loro altare, al fine di scongiurare la peste (o una piaga). Questo, tuttavia, era impossibile usando solo il metodo con riga e compasso di Euclide e lo stesso accadde per la trisezione dell’angolo. Invece, entrambi i problemi possono essere risolti utilizzando gli origami! Insomma, la Geometria degli origami è più potente di quella euclidea.
Il genio degli origami
Proprio come Euclide ideò gli assiomi per la Geometria planare, i matematici moderni Humiaki Huzita e Koshiro Hatori hanno ideato un insieme di assiomi per descrivere la Geometria degli origami: the Huzita–Hatori axioms (clicca qui per saltare gli assiomi e leggere il resto dell’articolo):
Assioma 1: dati due punti p1 e p2, c’è un'unica piega che passa per entrambi.
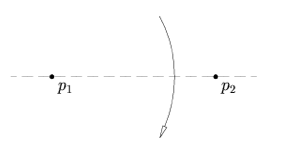
Assioma 2: dati due punti p1 e p2, c’è un'unica piega che porta p1 su p2.
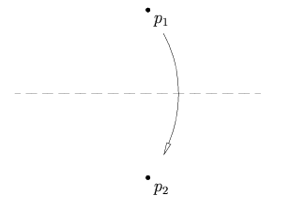
Assioma 3: dati due linee l1 e l2, c’è una piega che porta l1 su l2.
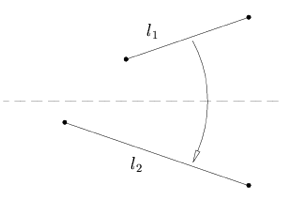
Assioma 4: dati un punto p1 e una linea l1, c’è un'unica piega perpendicolare a l1 che passa da p1.
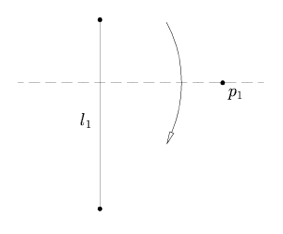
Assioma 5: dati due punti p1 e p2 e una linea l1, c’è una piega che porta p1 su l1 e che passa da p2.
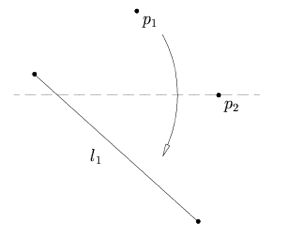
Assioma 6: dati due punti p1 e p2 e due linee l1 e l2, c’è una piega che porta p1 su l1 e p2 su l2.
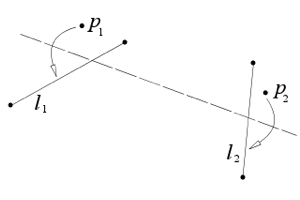
Assioma 7: dato un punto p e due linee l1 e l2, c’è una piega che porta p su l1 ed è perpendicolare a l2.
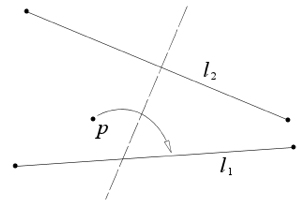
Trisezione dell’angolo
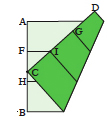
I sette assiomi sono la chiave sia per la trisezione dell’angolo sia per la duplicazione del cubo. Iniziamo con la costruzione dell’angolo. Seguendo le indicazioni descritte di seguito, è possibile vedere come questi semplici assiomi ci permettono di piegare la carta svolgendo un operazione impossibile per Euclide.
|
|
|
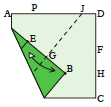
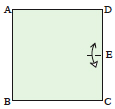
|
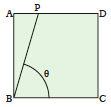
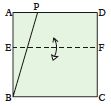
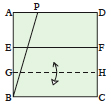
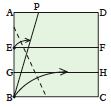
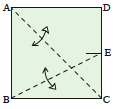
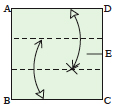
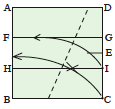
Disegna l’angolo desiderato PBC in modo che B sia in un angolo del quadrato. | Fai una piega orizzontale in un qualsiasi punto del quadrato, definendo la linea EF. | Piega la linea BC sulla linea EF e riapri il foglio, creando la linea GH. | Piega l’angolo in basso a sinistra in modo che il punto E tocchi la linea BP e il punto B la linea GH. |
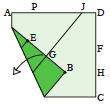
|
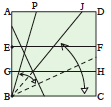
|
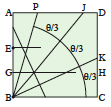
|
|
Con l’angolo B ancora in alto, piega entrambi gli strati per continuare la piega che finisce in G in modo che continui fino al nuovo punto J. | Riporta B nella posizione iniziale. | Piega lungo la linea che parte da J estendendola fino a B. Piega il lato in basso BC sulla linea BJ e riapro il foglio. | Le due pieghe BJ e BK dividono l’angolo originale PBC in tre parti uguali. |
Facendolo, potete convincere che la tecnica funziona. Per gli scettici, qui sotto c'è la dimostrazione. (NB: questo metodo funziona per angoli minori di 90°. C’è un altro metodo che funziona per gli angoli più grandi.)
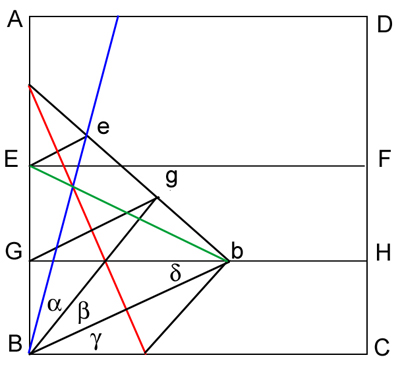
Dimostrazione della trisezione dell'angolo
Nell'imagine sotto l'angolo tra la linea blu e il lato inferiore è l'angolo da divdere in tre parti. Noi dobbiamo dimostrare che 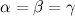 . La linea rossa è il solco risultante dal passaggio 4 della sequenza.
. La linea rossa è il solco risultante dal passaggio 4 della sequenza.
Ora guardiamo al triangolo 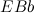 . Noi sappiamo che la lunghezza del segmento
. Noi sappiamo che la lunghezza del segmento 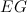 è uguale alla lunghezza del segmento
è uguale alla lunghezza del segmento 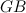 , e sappiamo anche che il segmento
, e sappiamo anche che il segmento 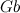 , altezza del triangolo
, altezza del triangolo 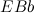 , è perpendicolare a
, è perpendicolare a 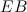 . In altre parole, l'altezza
. In altre parole, l'altezza 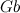 del triangolo divide il lato opposto in due metà. Questo significa che il triangolo
del triangolo divide il lato opposto in due metà. Questo significa che il triangolo 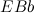 è isoscele.
è isoscele.
L'immagine speculare di 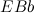 rispetto alla linea rossa è il triangolo
rispetto alla linea rossa è il triangolo 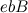 , anch'esso isoscele. La sua altezza, che esce da
, anch'esso isoscele. La sua altezza, che esce da 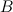 divide l'angolo in
divide l'angolo in 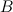 in due metà. Questo dimostra che
in due metà. Questo dimostra che 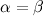 .
.
Per simmetria speculare noi abbiamo che 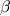 è uguale a
è uguale a 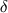 del triangolo
del triangolo 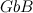 . E siccome
. E siccome 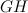 è parallelo al lato inferiore
è parallelo al lato inferiore 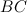 , noi abbiamo che
, noi abbiamo che 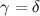 . Quindi
. Quindi 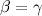 .
.
Duplicazione del cubo
Supponiamo di avere un cubo di lato s1 e volume V. Il compito è quello di trovare il lato s2 di un cubo avente volume 2V. Ecco come fare questa operazione usando gli origami.
|
|
|
|
|
Fai una piccola piega a metà del lato destro del foglio. | Segna due pieghe unendo i punti A e C e B ed E. Segnali bene solo nel punto in cui si incrociano. | Piega il lato superiore AD sul punto di intersezione e riapri. Quindi piega il lato BC a toccare la nuova piega e riapri. | Piega l’angolo C fino sul lato AB mentre il punto I deve giacere sulla linea FG. | Il punto C divide il lato AB in due segmenti. Trova il rapporto AC/CB e moltiplicalo per la lunghezza s1 del lato del cubo iniziale: il risultato è la lunghezza s2 che stai cercando. |
Se avete qualche dubbio, qui c’è la dimostrazione che la tecnica è corretta.
Dimostrazione della duplicazione del cubo
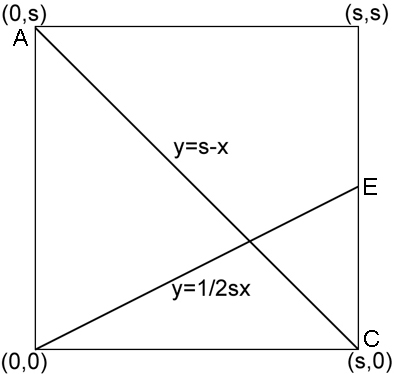 Figura 1
Figura 1 Prima di tutto mostriamo che i primi tre passaggi servono a dividere l'altezza del quadrato in tre parti uguali. Posizioniamo il quadrato in un sistema di coordinate con l'angolo 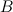 nel punto
nel punto 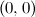 . Vedi figura 1. Ora la linea da
. Vedi figura 1. Ora la linea da 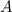 a
a 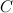 ha equazione
ha equazione
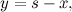
dove  è la lunghezza del latodel quadrato. La linea da
è la lunghezza del latodel quadrato. La linea da 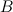 a
a 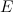 ha equazione
ha equazione
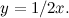
Quindi le due linee si incontrano in un punto con la coordinata  che soddisfa l'equazione
che soddisfa l'equazione
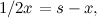
ovvero:
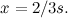
La coordinata 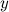 del punto di intersezione è quindi
del punto di intersezione è quindi
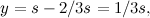
come richiesto.
La costruzione implica che il lato di misura 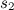 del nuovo cubo è
del nuovo cubo è 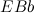 volte la lunghezza
volte la lunghezza 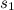 di un dato cubo. Ora siccome
di un dato cubo. Ora siccome ![$s_2 = \sqrt [3]{2}s_1$](/sites/default/files/media/images/img-0004_002.png) , noi abbiamo
, noi abbiamo
![$\sqrt [3]{2}s_1 = \frac{AC}{CB}s_1,$](/sites/default/files/media/images/img-0005_002.png)
quindi noi dobbiamo mostrare che ![$\frac{AC}{CB}=\sqrt [3]{2}.$](/sites/default/files/media/images/img-0006_002.png)
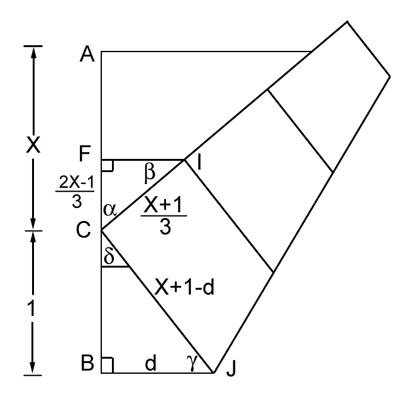
Figura 2
Prima di tutto, noi possiamo assumere che la lunghezza 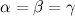 è uguale a 1, così possiamo scalare l'immagine come vogliamo senza cambiare le proporzioni. Noi scriveremo
è uguale a 1, così possiamo scalare l'immagine come vogliamo senza cambiare le proporzioni. Noi scriveremo 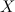 per la lunghezza del segmento
per la lunghezza del segmento 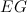 , quindi la lunghezza del lato del nostro quadrato è uguale a
, quindi la lunghezza del lato del nostro quadrato è uguale a 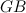 . Vedi la figura 2. Il segmento
. Vedi la figura 2. Il segmento 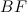 corrisponde a due terzi del lato del quadrato e quindi ha lunghezza
corrisponde a due terzi del lato del quadrato e quindi ha lunghezza 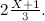 Ciò implica che la lunghezza del segmento
Ciò implica che la lunghezza del segmento 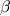 è
è
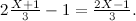
Scriviamo 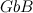 per la lunghezza
per la lunghezza 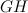 . SSiccome il segmento
. SSiccome il segmento 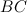 è parte del lato inferiore, la sua lunghezza è
è parte del lato inferiore, la sua lunghezza è 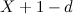 .
.
C'è un angolo retto in 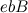 , quindi per il teorema di Pitagora abbiamo
, quindi per il teorema di Pitagora abbiamo
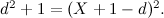
Questo significa
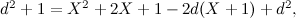
e quindi
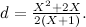
Ora consideriamo i due triangoli rettangoli 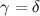 e
e 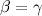 . Consideriamo che l'angolo di 180 gradi formato in
. Consideriamo che l'angolo di 180 gradi formato in 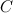 dal lato verticale, abbiamo
dal lato verticale, abbiamo![\[ \alpha =180-\delta -90 = 90-\delta . \]](/sites/default/files/media/images/img-0022.png)
Gli angoli del triangolo 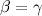 fanno 180°
fanno 180° ![\[ \gamma = 180 -90 - \delta = 90-\delta = \alpha . \]](/sites/default/files/media/images/img-0023.png)
quindi i triangoli 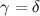 e
e 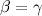 hanno due angoli uguali: l'angolo retto e l'angolo
hanno due angoli uguali: l'angolo retto e l'angolo 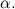 Questo significa che sono simili . Quindi, i rapporti dei lati corrispondenti dei due triangoli sono uguali. Osservando che
Questo significa che sono simili . Quindi, i rapporti dei lati corrispondenti dei due triangoli sono uguali. Osservando che 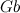 del triangolo
del triangolo 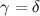 è la terza parte del lato del quadratoche ha lunghezza
è la terza parte del lato del quadratoche ha lunghezza 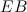 , abbiamo
, abbiamo ![\[ \frac{d}{X+1-d}=\frac{\frac{2X-1}{3}}{\frac{X+1}{3}}=\frac{2X-1}{X+1}. \]](/sites/default/files/media/images/img-0032.png)
Sostituendo l'espressione per 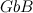 otteniamo
otteniamo![\[ \frac{X^2+2X}{X^2+2X+2}=\frac{2X-1}{X+1}, \]](/sites/default/files/media/images/img-0026.png)
quindi![\[ X^3+3X^2+2X=2X^3+3X+2X-2, \]](/sites/default/files/media/images/img-0027.png)
ovvero ![\[ X^3=2. \]](/sites/default/files/media/images/img-0028.png)
Questo è quello che volevamo dimostrare.
E’ tutta una questione di terzo grado
Cos’è che dà agli origami la forza di risolvere questi due problemi classici? La risposta sta nel fatto che entrambi questi problemi derivano dalla soluzione delle equazioni cubiche. Nel caso del cubo, basta guardare alla lunghezza di s2:
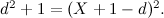
dove V è il volume di un dato cubo. Siccome V= s13, dove s1 è la lunghezza di un dato cubo, otteniamo:
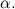
che diventa
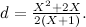
Siccome conosciamo s1, quello che dobbiamo trovare è proprio 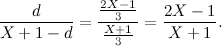 . Ed è questo il numero che abbiamo trovato con la costruzione precedente.
. Ed è questo il numero che abbiamo trovato con la costruzione precedente.
Sull’altro fronte, prendiamo un angolo 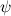 che può essere diviso in tre parti usando la trigonometria. Scriviamo
che può essere diviso in tre parti usando la trigonometria. Scriviamo 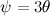 e applichiamo la formula trigonometrica per il coseno della somma di due angoli. Otteniamo quindi:
e applichiamo la formula trigonometrica per il coseno della somma di due angoli. Otteniamo quindi:
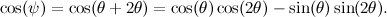
Ora sappiamo che 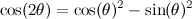 e che
e che 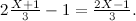
Sostituendo queste nell’equazione iniziale e semplificando otteniamo:
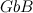
Risolvendo questa equazione cubica, troviamo i possibili valori di 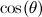 dai quali possiamo ottenere
dai quali possiamo ottenere 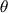 .
.
Gli origami non servono solo per risolvere queste due equazioni cubiche legate ai due problemi esposti ma ogni equazione cubica nella forma
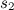
per qualsiasi a, b, c e d (puoi trovare delle informazioni su come farlo sul sito di Kashiro Hatori).
Quindi, mentre il metodo di Euclide può risolvere geometricamente le equazioni quadratiche usando solo riga e compasso, loro possono risolvere le cubiche.
Origami computazionali
Uno dei pionieri degli origami moderni basati sulla Matematica è Robert J. Lang, un matematico americano e artista di origami. Nel 1989, Lang scrisse un articolo per la rivista Engineering & Science nel quale si chiedeva se un computer potrà un giorno disegnare un modello per origami superiore a quelli disegnati dagli umani. Era una questione che lo appassionava al punto che, nel 1990, decise di scrivere un software che facesse ciò.
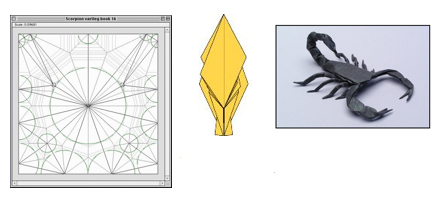
Da sinistra: pattern realizzato con il software TreeMaker, lo stadio iniziale e il modello finito. Immagine gentilmente concessa da Robert J. Lang.
Dopo diversi mesi, Lang produsse la prima versione di una parte del software che chiamò TreeMaker (poiché le figure di partenza da lui usate somigliavano a degli alberi). Il programma era in grado di convertire un disegno a mano libera, o una figurina, in uno schema dal quale il modello poteva essere piegato.
In questo ambito, lo schema è una figura geometrica che contiene un lembo per ogni appendice del modello da costruire. Così, una gru con due ali, una coda e una testa è formata da una base con quattro lembi mentre un insetto con sei zampe , una testa e un addome è formato da una base con 8 lembi.

Serpente a sonagli realizzato da Robert J. Lang. Immagine gentilmente concessa da Robert J. Lang.
All’inizio, TreeMaker era con le stesse parole di Lang “poco più di una curiosità matematica”. Tuttavia, nei successivi 8 anni, con la crescita della sua comprensione dei pattern per gli origami, Lang aggiunse diversi algoritmi al programma. Nel 1998, TreeMaker era in grado di costruire l’intero pattern per una gran varietà di origami. Oggi, Lang ha una collezione di migliaia di sculture origami. Anche se molte di queste sono state realizzate senza l’aiuto di TreeMaker, alcune delle più complicate sarebbero state impossibili senza esso. Le immagini di queste sue opere le abbiamo usate all’interno di questo articolo.
Tecnologia origami
Anche se alcune costruzioni di Lang (e di altri) sono stupefacenti, è facile ridurre gli origami a semplice arte: bella ma non applicabile nel mondo reale. Invece, si scopre con sorpresa che la tecnica degli origami è utilizzata in vari ambiti tecnologici, dai telescopi spaziali agli airbag delle automobili.

Alce realizzato da Robert J. Lang. Immagine gentilmente concessa da Robert J. Lang.
Da quando l’Hubble Space Telescope fu lanciato in orbita dallo space shuttle Discovery nel 1990, gli scienziati dello spazio hanno lavorato al suo probabile successore. Roderick Hyde del Diffractive Optics Group al Lawrence Livermore National Laboratory in Livermore (California, USA), uno a cui certamente non manca l’ambizione, porta avanti l’idea di costruire un telescopio quaranta volte più grande dell’Hubble. L’Hubble stesso non è proprio piccolo, con i suoi 13 metri di lunghezza e un’apertura di 2,4 metri. Il telescopio che propone Hyde avrebbe un’apertura intorno ai 100 metri e potrebbe raggiungere diverse centinaia di metri di lunghezza. Immediatamente si è posto il seguente problema logistico: anche se uno strumento simile può essere progettato, come si fa a mandarlo in orbita?
La risposta arriva nel momento in cui ci si rende conto della possibilità di costruire delle lenti ripiegabili che possono essere impacchettate in uno space shuttle. La distanza tra i due estremi del telescopio può semplicemente essere ottenuta posizionando in orbita due lenti a un’adeguata distanza, dove una minor forza gravitazionale permette ad essi di rimanere. Vedendo immediatamente il collegamento con la piegatura della carta, il laboratorio ha contattato Robert J. Lang per chiedere un’opinione.
Negli anni successivi, e con l’aiuto di Lang, il team ha costruito un prototipo che si chiama Eyeglasses che ha cinque metri di diametro. L’attuale successore di Hubble, il James Webb Space Telescope, sarà lanciato nel 2013 e avrà degli specchi che si ripiegano come origami per essere trasportati dal missile.
Un’applicazione più comune, come lo sviluppo degli airbag delle automobili, mostra un altro esempio di utilizzo degli origami. Prima che l’airbag si gonfi durante un incidente, esso è piegato in uno spazio ristretto all’interno del volante o del cruscotto. Gli ingegneri hanno disegnato gli airbag modellando il processo di gonfiaggio sul computer. Per farlo, necessitavano di un algoritmo attraverso il quale potevano piegare l’intero airbag.
Usando un algoritmo dal suo software TreeMakers, Lang fu in grado di fornire agli ingegneri della German company EASi Engineerin una soluzione per un dato prolema. Essenzialmente si è trattato di rappresentare un airbag come una serie di poligoni, i cui lati rimangono allineati durante e dopo la piegatura, sistema che può essere ottenuto con un dettagliato pattern di piegatura come quelli usati da Lang per i suoi origami.
Maestro di origami
Per un arte antica come l’invenzione della carta, gli origami hanno avuto bisogno di molto tempo per raggiungere il proprio potenziale. Oggi centinaia di altre applicazioni sono state scoperte, dall’aiutare i robot ad autoassemblarsi a fornire indizi di come le proteine di pieghino in strutture tridimensionali precise nel corpo umano. Ci sono voluti circa 200 anni e la nascita dei computer per realizzare tutto ciò che è realizzabile e le creazioni di Lang sono testimonianza del punto a cui siamo arrivati.

Mantide realizzata da Robert J. Lang. Immagine gentilmente concessa da Robert J. Lang.
L’incredibile applicazione degli origami ha messo fine alle mie iniziali illusioni di grandezza e al credere di aver conquistato il mondo degli origami a nove anni con una gru di carta. Tuttavia, per i novelli origamisti, il piacere della scoperta di poter realizzare anche una semplice ed elegante forma soltanto da un foglio di carta e qualche piega può far pensare a chiunque di essere un maestro in quest’arte. Andate avanti, vi esorto a continuare a provare e vi garantisco che ne verrete rapiti.