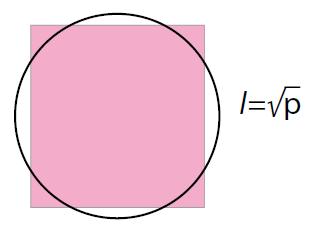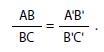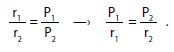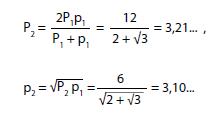Numeri e forme geometriche

Su e giù per le costanti matematiche

I numeri misurano, calcolano, esprimono il ca­rattere quantitativo delle cose, ma è difficile riconoscere loro una qualche caratteristica autonoma e trattarli come amici.

Alcuni numeri particolari, tuttavia, si staccano dal loro ruolo di quantità per farci conoscere qual­cosa degli oggetti – figure, forme, solidi… solitamente oggetti importanti per la nostra cultura – con i quali entrano in contatto.

È questo il caso, ad esempio, di √2, che ci dice qual è il rapporto fra la diagonale ed il lato di un quadrato e questo è vero per tutti i quadrati, come si capisce facilmente dal teorema di Pitagora. Oppure è il caso della base dei logaritmi naturali

e=2,71828182845904523536...

un numero che non ha una definizione proprio semplice e che, quasi magicamente, ci permette di descrivere in pratica tutte le leggi di accrescimento esponenziale.

È il caso anche del “numero aureo” Φ=(1+√5)/2 (la soluzione positiva dell’equazione x²-x-1=0) che, a partire dal mondo classico, esprime il rapporto ideale fra i lati di un rettangolo, nel senso di fornire il canone riconosciuto di bellezza per rapporti di questo tipo.

La sezione aurea nel Partenone - Foto di Eusebius modificata/Creative commons license.

È significativo che questo canone di bellezza intervenga in tutte le situazioni naturali di “simmetria dinamica”: nella forma di certe conchiglie, nelle spire con cui dispongono i semi di certi fiori, o le foglie di certi alberi, nella struttura delle corna dell’ariete, nella disposizione dei bracci di una galassia, nei percorsi dei falchi in volo che si avvicinano alla preda….

Simmetria dinamica [da sinistra: Conchiglia di Nautilus (foto di Chris 73/Creative commons license); Girasole (foto di Канопус Киля/Creative commons license); Ariete in bronzo (foto di Giovanni Dall'Orto/Creative commons license); Galassia a spirale (foto di hubblesite/Creative commons license)]

I matematici hanno formalizzato tutti questi processi con la "spirale logaritmica", detta anche "spira mirabilis" per la sua forma, descritta per la prima volta ed ammirata per il suo aspetto esteriore da Cartesio.

Spirale logaritmica - spira mirabilis

Questo ruolo conoscitivo – sia del mondo naturale che di quello artificiale costruito dall’uomo o da quello creato dall’uomo con le sue teorie scientifiche – è assegnato in generale a tutte le cosiddette “costanti matematiche”.

Talvolta l’origine di queste costanti ha avuto un risvolto drammatico. Come nel caso di √2. A quanto racconta il mito, Ippaso da Metaponto, un seguace della scuola pitagorica, nel V secolo a.C. fu condannato severamente per aver rivelato che il rapporto fra diagonale e lato di un quadrato non si esprime razionalmente, cioè come rapporto di numeri interi. Un risultato che non era sicuramente semplice da trovare in quell’epoca ma che noi oggi, con il formalismo moderno, siamo in grado di dimostrare facilmente: se fosse √2=m/n (con m ed n interi) allora si avrebbe 2n²=m² e questo entra in contraddizione con il cosiddetto “Teorema fondamentale dell’aritmetica”, grazie al quale ogni numero intero si scompone in maniera unica come prodotto di fattori primi. In questo caso si capisce che, in 2n², il fattore primo 2 compare un numero dispari di volte mentre in m² (se compare) il fattore primo 2 non può che esserci un numero pari di volte. Come possono dunque essere uguali quei due numeri? Dove finirebbe l’unicità della scomposizione?

In questo caso, l’aspetto drammatico e la punizione inflitta al colpevole dipendono della forma di conoscenza racchiusa in √2 che era intollerabile per la cultura della scuola pitagorica: tutti gli oggetti, le quantità, le misure, i loro rapporti dovevano esprimersi attraverso i numeri interi.

Noi oggi sappiamo che questo non è vero, che nel mondo non è sempre così. Esistono numeri che non sono razionali  e per usarli è necessario ricorrere ad una loro approssimazione. Ad esempio, oltre a √2, la sezione aurea Φ o il numero e visti in precedenza o anche numeri dal carattere più “difficile”. Tuttavia oggi, anche se alcune “costanti matematiche” che compaiono nei nostri conti, richiedono molto lavoro per approfondire le loro proprietà o addirittura per “inventare” un ambiente numerico nel quale ha senso considerarle, non risultano certamente intollerabili per la nostra cultura. Per √2, Φ ed e si è introdotto il dominio dei numeri irrazionali, per un’altra costante famosa (i, caratterizzata da i² = -1) i matematici hanno dovuto inventare i numeri “immaginari” così detti perché, quando sono nati (alla fine del ‘500), si riconosceva il loro carattere artificiale, estraneo al sistema dei numeri che era noto fino ad allora.

Fra queste costanti, forse la più antica – visto che ne parla implicitamente perfino la Bibbia, seppure con una approssimazione molto grossolana – è senz’altro π che fornisce il rapporto di ogni circonferenza con il proprio diametro (e anche di ogni cerchio con il quadrato del raggio). Una costante che, per quanto se ne sa, non ha mai alimentato drammi ma domande e misteri sì. E molti. E nel tentativo di capire proprio i misteri di π, i matematici hanno sviluppato molta buona Matematica.

“Esplorare π è come esplorare l’universo”, dice David Chudnovsky, uno dei grandi “esploratori” in questo senso.

In effetti π si incontra dovunque in Matematica. Per capire questa sua presenza sistematica fin dai tempi più antichi, bisogna ricordare soprattutto che π ci parla della circonferenza e la circonferenza è una delle prime forme studiate dall’uomo, addirittura simbolo di perfezione perché capace di trasformarsi in se stessa, come la retta, e forse rappresenta la componente e il modello di molte forme geometriche.

Sappiamo, ad esempio, che la antica cosmologia tentava di descrivere il moto dei corpi celesti attraverso complicate combinazioni di moti circolari. Sappiamo che tutte le costruzioni geometriche dovevano essere condotte solo con l’uso di riga e compasso. Uno dei grandi problemi della Matematica classica era la “quadratura del cerchio”, vale a dire il problema di trovare, usando solo questi strumenti, il lato di un quadrato di area uguale a quella di un cerchio. Oggi sappiamo che questo problema non è risolubile, perché richiede la costruzione con riga e compasso di un segmento di lunghezza √π, mentre con questi strumenti si possono costruire solo segmenti la cui misura sia soluzione di un’equazione di secondo grado (o quarto, o ottavo, sedicesimo e così via). Ma √π non è di questo tipo, come è stato scoperto solo nel 1882: quanto lavoro intellettuale!

Quadratura del cerchio

Questa presenza sistematica e misteriosa di π – che cresce anziché diminuire nel tempo –  richiede rispetto, in riconoscimento della sua importanza. Ma, allo stesso tempo, nei confronti di π è in corso da secoli anche una sfida alla capacità di calcolo dell’uomo e delle sue macchine, come si capisce tenendo conto dei ripetuti ed insistenti tentativi per calcolare una quantità sempre maggiore di cifre decimali. Pensate che, con l’uso dei calcolatori più potenti, ne è stata trovata a tutt’oggi qualche decina di miliardi.

Questa ricerca ha senz’altro importanti ricadute sulle tecniche di calcolo, sulla tecnologia delle macchine e sullo studio delle possibili regolarità statistiche (che tuttavia finora non sono mai saltate fuori). Ma, secondo me, la motivazione principale che muove questi “cacciatori” di decimali di π è la sfida nelle capacità umane. Come quando si vuole superare un “record” sportivo, compiere un’impresa mai riuscita in precedenza, anche i matematici si pongono obiettivi ambiziosi che forse, per chi guarda solo con il metro del vantaggio immediato, possono sembrare inutili.

I misteri di π

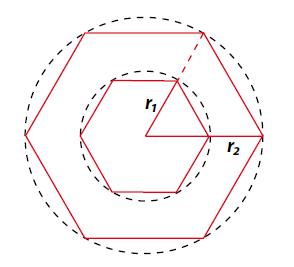
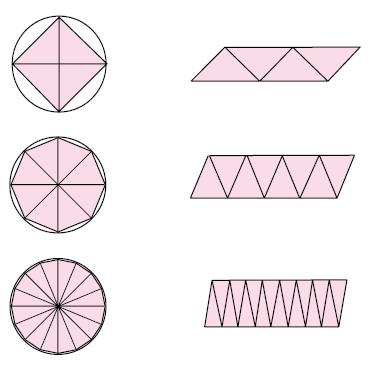
Come hanno capito gli uomini che il rapporto fra circonferenza e diametro è una costante, uguale per tutte le circonferenze, e che è la stessa che lega il raggio del cerchio alla sua area? Si può pensare che, dopo calcoli pratici e in seguito ad osservazioni empiriche, si siano concettualmente convinti che questo è vero per estensione del fatto che vale per i poligoni regolari inscritti nella circonferenza, aumentando progressivamente il numero dei lati.

Il rapporto fra i perimetri dei poligoni regolari inscritti è uguale al rapporto dei raggi

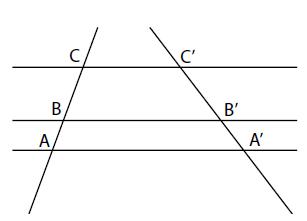
Consideriamo due cerchi concentrici, con raggi r1 e r2 e, inscriviamo in essi due poligoni regolari con uguale numero di lati. È facile dimostrare che il rapporto fra la lunghezza dei lati (e di conseguenza fra i  perimetri P1 eP2 dei poligoni) è uguale al rapporto fra i raggi. Per avere questo risultato basta ricordare il teorema di Pitagora e il teorema di Talete sui fasci di rette parallele:

Un fascio di rette parallele taglia su due trasversali segmenti direttamente proporzionali:

Fascio di rette parallele

Ora si ricava subito che il rapporto fra perimetro e raggio è una costante:

Il perimetro di un poligono inscritto è una “approssimazione” della circonferenza C. È sempre minore di C e l’approssima sempre meglio quanto più è grande il numero dei lati: prendendo un poligono regolare con un numero di lati sempre maggiore ci si avvicina sempre meglio alla lunghezza della circonferenza.

Ha senso considerare che la circonferenza sia “un poligono regolare con infiniti lati”? In termini formali no. Ma intuitivamente questa è una buona immagine. Se poi si considera un argomento analogo con poligoni regolari circoscritti, il cui perimetro è sempre maggiore di C e si avvicina sempre più a C quanto più aumenta il numero di lati, non è difficile convincersi che C è l’unico valore che sia maggiore del perimetro di qualunque poligono regolare inscritto ed allo stesso tempo minore del perimetro di qualunque poligono regolare circoscritto. La conclusione che anche il rapporto fra la circonferenza C ed il raggio r (o il diametro 2r) sia costante, sempre lo stesso per tutti i cerchi è intuitivamente a portata di mano e i matematici hanno reso formalmente precisa questa dimostrazione con l’operazione di “passaggio al limite”.

Il rapporto con il diametro ha preso il nome di π (non da subito, solo dal ‘600):

C/2r = π

Ma quanto vale π ? Il primo calcolo accurato è attribuito ad Archimede di Siracusa (III secolo a.C.) che, come nella discussione precedente, considera progressivamente poligoni inscritti e circoscritti alla circonferenza di raggio 1 (e quindi semiperimetro π) con 6, poi 12, 24, 48 e infine 96 lati. In generale, con ragionamenti di tipo geometrico, riesce a esprimere come variano i semiperimetri di questi poligoni, che approssimano sempre meglio π, quando si raddoppia il numero dei lati.

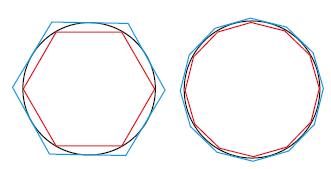
Poligoni inscritti e circoscritti

Per l’esagono il semiperimetro interno vale p1=3 e quello esterno P1=2√3=3,46.. . Dunque, in prima approssimazione:

 3≤π≤3,46

Ma poi, raddoppiando il numero dei lati, ottiene:

e quindi la successiva approssimazione:

3,10≤π≤3,21

Applicando sempre la stessa formula per ogni successivo poligono inscritto e circoscritto, Archimede ottiene la migliore approssimazione con 96 lati:

3,1408...=223/71<π<22/7=3,(142857)

L’errore è solo nella terza cifra decimale: un millesimo. Complimenti!

Con un discorso simile a quello della circonferenza, si può dimostrare anche che π interviene nel rapporto fra area e quadrato del raggio. A questo scopo, approssimate ancora il cerchio con un poligono regolare inscritto e pensate di aumentare il numero dei lati. L’area del cerchio si approssima con una somma di triangoli isosceli: con un quadrato sono quattro triangoli rettangoli, con un ottagono sono otto triangoli aventi un angolo al vertice di 45^o, con un poligono di sedici lati….

Sviluppo dell’area

L’angolo al vertice è sempre più stretto e l’area del cerchio si avvicina sempre più a quella di un rettangolo che ha la circonferenza C = 2πr come base ed il raggio r come altezza. Ecco giustificata in termini intuitivi la formula dell’area S:

S = πr².

Al solito: questo fatto verrà completamente dimostrato con una operazione di  “passaggio al limite”. E allora, per concludere, un cenno di attenzione su questa che sembra risolvere magicamente tutte le situazioni.

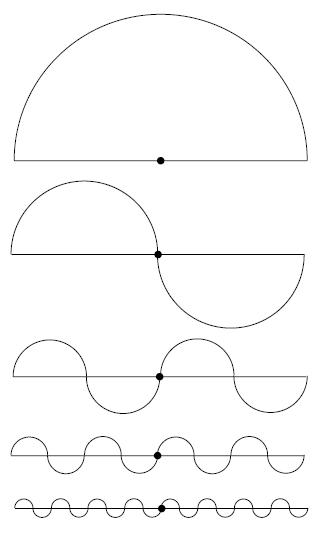
Esercizio: prendete una semicirconferenza di raggio uguale ad 1. Sulla sua base costruite due circonferenze di raggio 1/2. Convincetevi  che la lunghezza complessiva del percorso appena disegnato è uguale alla semicirconferenza, cioè a π. Ora continuate con la stessa operazione e costruite quattro semicirconferenze di raggio 1/4: la lunghezza del percorso totale è ancora uguale a π. Via così, con circonferenze di raggio dimezzato ogni volta: è chiaro che il percorso complessivo è sempre uguale a π. Sì, ma questo percorso “tende” ad approssimare sempre più il diametro della circonferenza, che vale 2. E allora? Attenzione: non è tutt’oro quel che luccica e il passaggio al limite funziona solo nelle ipotesi giuste.

Questo non è un limite!