Simmetria e matematica 1

Per cominciare

Il valore della simmetria ... e della sua assenza

Mi piace pensare che tanto tempo fa la simmetria fosse soprattutto una proprietà estetica. Con questo valore viene ancora oggi considerata in ogni rappresentazione artistica, in particolare in ogni espressione dell'arte figurativa. Ma, allo stesso tempo, è chiaro che, fin dai periodi più antichi, proprio la simmetria delle figure incorporava in sé i germi di una prima, rudimentale, forma di osservazione scientifica, come se qualche nostro acuto progenitore avesse scoperto che, attraverso le figure, si trasmettono idee e concetti e che la simmetria fornisce un primo, elementare, principio di classificazione. E forse è proprio avvenuto così: si veda la Figura 2.1 nella quale alcune semplici rappresentazioni del sole, risalenti a periodi antichissimi - paleolitico superiore e poi neolitico - con la loro simmetria colgono in maniera ingenua un dato che in seguito si è manifestato chiaramente alla coscienza dei ricercatori: "lo spazio è omogeneo e isotropo" - il sole irraggia in ugual misura in tutte le direzioni.

Figura 2.1 Antiche rappresentazioni del sole (tratte dal libro di Slavik Jablan [4] )

 Anche la mancanza di simmetria esprime inaspettate relazioni. L'articolo di Caglioti in questo volume mette in luce il senso di un profondo e istruttivo aforisma che risale alla cultura Zen: "la vera bellezza è una deliberata, parziale, rottura di simmetria". Ebbene, anche qui, con un po' di buona volontà, si ritrovano alcune categorie di pensiero che partecipano di ogni autentica ricerca e che si possono chiamare a buon diritto "scientifiche".

Si possono leggere: la negazione della tesi con un'azione voluta e provocatoria, il valore sperimentale, l'intervento sui particolari e il desiderio di saggiare la tenuta del tutto.

Che la stessa idea sia anche presente fin dai primordi nella cultura occidentale è testimoniato da antiche raffigurazioni pittoriche, come, per esempio, quelle della Figura 2.2, risalenti al periodo egiziano, nelle quali la rottura di simmetria rende attuale il gesto e contribuisce a conferire all'intera scena la vivacità del movimento reale.

 
Figura 2.2 Fregi di Saqqara

 Sul tema della simmetria, in particolare sul suo contenuto estetico e il suo intreccio con le strutture matematiche, sono stati scritti numerosi libri, alcuni dei quali rappresentano una lettura piacevole e per niente difficile. Sopra tutti vale la pena di indicare il bel libro di Hermann Weyl [7], una raccolta di conferenze tenute dall'autore negli anni 'S0 del secolo scorso, al momento del suo abbandono dell'attività didattica. Sulla rottura di simmetria in vari settori artistici e scientifici rimane di grande interesse l'affascinante libro di Giuseppe Caglioti [2]. Altri utili testi nei quali le considerazioni formali si alternano sistematicamente con l'analisi di forme e figure sia piane che spaziali, così come alcuni siti piacevoli da leggere o semplicemente da guardare e consultare, saranno consigliati di volta in volta oppure dati direttamente in bibliografia. Ora l'argomento è questo: quale apporto ha dato la matematica alla simmetria e, viceversa, qual è la formalizzazione matematica di questa affascinante relazione delle figure?

...in matematica

La simmetria per la matematica del mondo antico

Per quanto riguarda la simmetria, la matematica prende sul serio il principio dinamico che ne sta alla base, perché la simmetria di una figura è definita attraverso le trasformazioni dell'ambiente in cui la figura si trova. In matematica si dice che è una "proprietà invariante" rispetto a quelle trasformazioni. Nello spazio euclideo, per esempio, cioè nello spazio che formalizza la nostra esperienza delle forme geometriche, la simmetria si manifesta attraverso tutti i movimenti rigidi che lasciano fissa la figura.

Così, in primo luogo, in matematica la simmetria si presenta come una relazione geometrica. Tuttavia la sua trattazione sistematica e formale si è affacciata in maniera diversa, attraverso l'algebra, sotto la forma dei "gruppi di simmetria" relativi alle soluzioni delle equazioni dei vari gradi: i "gruppi di Galois", che prendono il nome da Evariste Galois, il giovane e sfortunato matematico che li ha introdotti nella prima metà dell'800 (più avanti si vedrà un accenno alla nozione di "gruppo"). La formalizzazione del concetto di simmetria ha dunque visto la luce abbastanza tardi e non attraverso la geometria, anche se, naturalmente, le considerazioni geometriche hanno sempre avuto grande importanza.

Nel periodo della classicità greca la simmetria era senz'altro uno dei caratteri principali delle figure. Tale appariva sicuramente nei risultati teorici che, nel VI secolo prima di Cristo, sono attribuiti a Talete di Mileto e che vengono riconosciuti come i "primi" autentici teoremi della nostra cultura occidentale. Eccoli, brevemente rappresentati nella Figura 2.3.

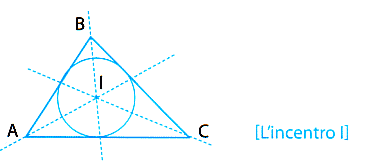
Figura 2.3 I teoremi di Talete

ogni diametro divide il cerchio in due parti uguali;

gli angoli alla base di un triangolo isoscele sono uguali;

angoli opposti al vertice sono uguali;

angoli inscritti in una semi-circonferenza sono retti.

Anche senza una dimostrazione formale di queste proprietà, già guardando la figura, si intuisce che le considerazioni sintetiche, di natura simmetrica, quasi a colpo d'occhio sono sufficienti per convalidarle in modo concettuale e accettarle. Questa modalità riguarda anche altri aspetti della matematica greca: è noto per esempio che, presso la scuola pitagorica, il desiderio esplicito di rivelare l'armonia dell'universo attraverso le relazioni numeriche fra gli enti si basava largamente su considerazioni di regolarità e dunque di simmetria. Si vedano per questo le nozioni relative ai vari tipi di numeri: triangolari, quadrati, pentagonali... (Figura 2.4) che, assegnando loro una forma definita, permettono di visualizzare e analizzare le quantità in termini geometrici.

Figura 2.4 Numeri triangolari quadrati, pentagonali ...

Ma le dimostrazioni a colpo d'occhio non bastano. In seguito, gli studiosi dei periodi successivi, quello ateniese e poi quello alessandrino, allo scopo di affrontare nuovi e più complessi problemi introdussero orgogliosamente il principio della deduzione formale, e furono perfino condotti a considerare la visione sintetica quasi come un limite, se non un ostacolo, all'avanzamento della matematica. In questo modo, sia i progressi della scuola geometrica ionica che i vantaggi dell'estetica numerica dei pitagorici persero gradualmente interesse. Ma il sacrificio risultò necessario per il progresso della materia e l'affermazione del rigore dei metodi.

In Euclide, nel III secolo avanti Cristo, la simmetria compare spesso come sinonimo di commensurabilità, nella trattazione di segmenti che si possono misurare razionalmente l'uno rispetto all'altro. Nella sua opera è presente anche la classificazione dei poliedri regolari, i cosiddetti "solidi platonici" (Figura 2.5) -un risultato di grande valore, tanto che a ciascuna delle cinque forme venne assegnato un significato cosmologico. Ma, forse a causa della riluttanza di Euclide a considerare gli aspetti dinamici dei corpi, la ricca simmetria dei solidi regolari sembra quasi un fatto occasionale, una singolarità della figura piuttosto che una relazione che il solido ha con lo spazio in cui è immerso. Senza movimento, non si mette in luce la simmetria... anche se, paradossalmente, questa è proprio ciò che non cambia. Per Vitruvio, nel De Architectura -e siamo nel I secolo avanti Cristo- la simmetria denota una relazione fra il tutto e le sue parti e qui sembra iniziare ma anche concludersi l'esperienza nel mondo latino. Almeno per quanto ne sappiamo. Il termine stesso, "simmetria", sembra scomparire e ripresentarsi solo nel Rinascimento, teso alla riacquisizione della cultura classica e allo stesso tempo alla valorizzazione della osservazione e della costruzione umana.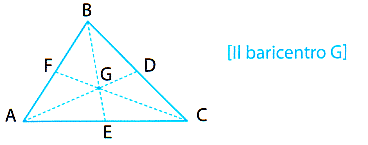

Figura 2.5 I cinque solidi platonici

Nasce la scienza moderna: Hermann Weyl [7] attribuisce a Leonardo da Vinci, impegnato nello studio e nella migliore utilizzazione delle piante degli edifici, uno dei primi risultati relativi alla simmetria geometrica.

A partire dal '500 la simmetria si insinua nell'algebra: vengono trovate le formule risolutive delle equazioni di terzo e poi di quarto grado -risultati di straordinario valore. E la fiducia che anche le equazioni di grado superiore al quarto si possano risolvere per mezzo delle consuete operazioni aritmetiche e dell'estrazione di radice impone di approfondire le proprietà che legano le soluzioni ai coefficienti dell'equazione. Sono le "funzioni simmetriche" a fornire il principale metodo di studio delle equazioni algebriche e, nell'800, a permettere grazie alle geniali intuizioni di Galois, di trasformare il problema. Non è tanto importante che si dimostri in maniera precisa che, per le equazioni di grado superiore al quarto, una formula risolutiva di quelle sperate non è possibile da trovare. I metodi usati per raggiungere questo scopo si sono dimostrati in fondo più importanti del problema stesso e ormai la strada è aperta per collegare una struttura a un problema. Grazie alla simmetria è stato fatto il passaggio che caratterizza l'algebra moderna: dalle quantità alle strutture.

In campo geometrico la simmetria non ha ancora fatto la sua comparsa formale: i primi, fondamentali, risultati sulle forme dello spazio sono ottenuti nelle ricerche cristallografiche e solo in seguito vengono ritrovati e dimostrati rigorosamente dalla geometria. Ma questo avverrà all'inizio del '900.

Il linguaggio

Descrivere, riconoscere, classificare la simmetria

Limitiamoci a considerare le figure del piano rispetto alle "isometrie", vale a dire alle corrispondenze biunivoche del piano in sé che conservano le distanze fra punti corrispondenti: se T è la corrispondenza e d(A,B) denota la distanza fra due punti, T è un'isometria quando, per ogni coppia di punti A e B del piano vale:

 d(T (A),T (B))=d(A,B)

È chiaro che allora sono conservati anche gli angoli, la cui misura si esprime per mezzo del rapporto di due segmenti. Vedremo più avanti una classificazione delle isometrie del piano. Ora la definizione principale: se F è una figura, una "simmetria" di F è una isometria che trasforma Fin se stessa (pur senza trasformare in sé ogni singolo punto). In simboli: T(F) = F.

Tre importanti modalità del pensiero scientifico, come avviene per ogni settore di studio, sono direttamente connesse al problema della simmetria in campo geometrico. In primo luogo occorre dotarsi di un simbolismo che permetta di parlare degli elementi fondamentali della simmetria e delle loro relazioni. In altri termini, trovare una notazione formale, precisa ed espressiva. Per esempio, in un "fregio" F, in principio indefinito, come il seguente:

....NONONONO....

si ha un "modulo" elementare (in questo caso la forma NO) che subisce una traslazione in entrambi i versi. Inoltre, esistono molti centri di rotazione di angolo uguale a π per il fregio: non esistono altre isometrie di F. Il simbolo p112 esprime compiutamente questa situazione: qui, p indica la presenza di una traslazione, mentre 2 è il periodo delle rotazioni e i due 1 intermedi sono semplicemente dei "segnaposto", che indicano la possibilità, ma in questo caso l'assenza, di altre simmetrie del modulo.

Per il fregio seguente invece:

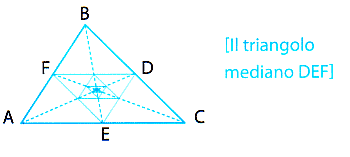
oltre alla traslazione del modulo ed alle rotazioni di periodo 2 esistono anche altre simmetrie. In questo caso è utile ricorrere al valore posizionale dei simboli usati: si tratta di un fregio pmg2 che, rispetto al precedente, ha numerose riflessioni con asse ortogonale alla direzione della traslazione - espresse dalla lettera m (che sta per mirror) in seconda posizione -ed una glissoriflessione (g per glide, si vedrà più avanti di quale isometria si tratta) in terza posizione- necessariamente con asse orizzontale.

II simbolismo, la sua precisione e la sua univocità sono sempre una conquista che permette di parlare degli elementi fondamentali dello studio. Ma questo non basta. Occorre anche essere in grado di riconoscere la somiglianza o la differenza delle situazioni che possono presentarsi nei diversi casi: confrontare due modelli apparentemente diversi e scoprire se hanno oppure no la stessa simmetria. Si vedano per esempio i due fregi della Figura 2.6. Non è difficile riconoscere che entrambi sono del tipo pmg2.

Figura 2.6 Due fregi di tipo mpg2

Dunque sono due fregi che, per la nostra classificazione, vanno identificati.

In qualunque metodologia scientifica, i problemi di rappresentazione e riconoscimento sono fondamentali, in quanto forniscono il linguaggio simbolico e corrispondono all'operazione logica "uguaglianza/differenza". Ma il matematico non si accontenta di questa prima capacità operativa e desidera raggiungere una forma più profonda di conoscenza. Occorre delimitare il proprio orizzonte nello studio: quali sono tutti i possibili fregi? - si chiede in questo contesto. Il desiderio di classificare richiede certamente un linguaggio opportuno e abilità nel riconoscere i diversi modelli, ma anche la nuova capacità di dedurre e portare la ricerca a esaurimento dei casi possibili. Per questo, per capire in quanti e quali modi può articolarsi la classificazione, è necessario indagare più profondamente l'insieme delle simmetrie di F.