Un approccio "laterale" alla congettura di Collatz

Il matematico ungherese Paul Erdös, a proposito della congettura di Collatz disse: "La matematica non è ancora pronta per problemi di questo tipo". Una tale affermazione farebbe desistere dal cimentarsi nella sua risoluzione, ma esistono problemi che sono stati risolti, non con il ragionamento matematico di tipo consequenziale a cui allude Erdös, bensì con quello laterale (che può procedere anche a salti). Ne è un esempio la costruzione dei quadrati magici, la cui dimostrazione matematica, infatti, viene ricavata a posteriori, una volta trovata la soluzione tramite un ragionamento di tipo laterale.

Visivamente, la differenza tra i due approcci può essere illustrata nel seguente modo: con il ragionamento consequenziale si può costruire un muro mettendo file di mattoni l'una sopra l'altra, ma se si vuol costruire un arco, i mattoni non si reggono, quindi occorre fare un salto logico: usare un supporto nella certezza che mettendo l'ultimo mattone la costruzione reggerà ed il supporto si potrà togliere. L'approccio che è stato usato con successo in quei tipi di problemi vorremmo utilizzarlo anche in questa sede, pur consapevoli che si tratta di questioni molto diverse e quindi diversa sarà l'applicazione e aperta rimarrà la valutazione sull’esito finale.

La congettura, enunciata per la prima volta nel 1937 dal matematico tedesco Lothar Collatz (1910-1990), da cui prende il nome, asserisce che:

Preso un qualsiasi numero positivo intero n e applicando il seguente algoritmo:

a) se n=1, l'algoritmo si conclude;

b) se n è pari, lo si deve dividere per 2, altrimenti lo si deve moltiplicare per 3 e aggiungere 1 dando luogo a una successione di numeri che si concluderà quando si otterrà il valore 1.

ovvero

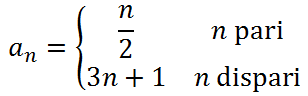
L'algoritmo giungerà sempre a conclusione, indipendentemente dal valore di partenza di n.

Nel caso in cui si verificasse che la successione non arrivasse a contenere 1, perché illimitata superiormente o perché con le suddette operazioni la successione entra in un ciclo che si ripete senza mai dare 1, la congettura risulterebbe falsa.

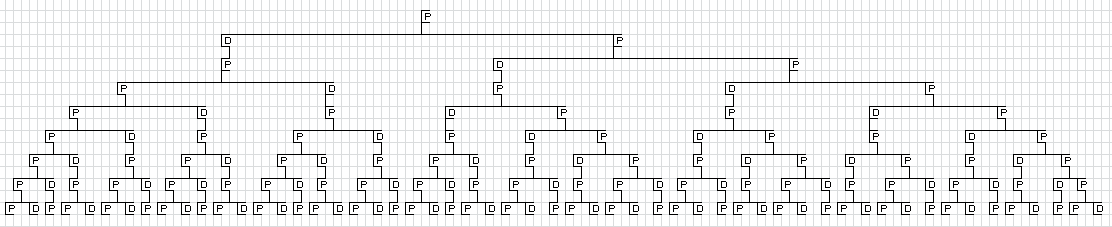
Iniziamo il nostro lavoro analizzando il diagramma ad albero rovesciato dei numeri pari e dispari che si ottengono a ogni passaggio dell'algoritmo.

Il fatto di essere partiti da un numero pari non inficia quanto segue poiché qualsiasi numero dispari si trasforma in pari al passaggio successivo.

Nel file Excel allegato a questo lavoro, a fianco del diagramma, abbiamo riportato la quantità di numeri pari e quella di numeri dispari presenti in ogni sua riga; abbiamo poi calcolato il rapporto tra la prima e la seconda quantità e abbiamo rilevato che, dalla sesta riga in poi si attesta a un valore leggermente superiore a 1,6 per poi mantenersi costante al valore di 1,618033988749890 dalla 40^a in poi.

Facciamo notare che il diagramma l'abbiamo costruito soltanto per le prime nove righe, ma il calcolo dei pari e dei dispari sopra riportato è agevole da fare poiché ogni riga ha come valore la somma delle due righe precedenti.

Per la proprietà commutativa sappiamo che in una moltiplicazione, cambiando l'ordine dei fattori i prodotto non cambia, pertanto moltiplicare un numero n x volte per 3 è equivalente a n×3^x e moltiplicare un numero n y volte per 1/2 è equivalente a n×(1/2)^y.

Avendo constatato che, per ogni riga del diagramma, il rapporto tra quantità di numeri dispari e quantità di pari è di 1:1,61803398749890 che possiamo arrotondare (a nostro svantaggio) a 1,6, verifichiamo per quale valore minimo di x numero positivo intero, accade che anche y sia un numero intero: il risultato è: x=5 e y=8.

A questo punto, sostituendo i valori di x e y abbiamo che: 3^x=3⁵=243 e 2^y=2⁸=256.

Essendo 256>243 l'algoritmo tenderà a far convergere il valore di n verso il basso e tale tendenza crescerà in modo esponenziale a ogni passaggio dell'algoritmo (corrispondente a un'ulteriore riga del diagramma) infatti, mantenendo sempre il rapporto di tra quantità di numeri dispari e quantità di pari 1:1,6 abbiamo che:

per x=5 e y=8 si ha: 2⁸/3⁵=1,053

per x=10 e y=16 si ha: 2¹⁶/3¹⁰=1,109

per x=50 e y=80 si ha: 2⁸⁰/3⁵⁰=1,683

per x=100 e y=160 si ha: 2¹⁶⁰/3¹⁰⁰=2,835

per x=200 e y=320 si ha: 2³²⁰/3²⁰⁰=8,041

per x=300 e y=480 si ha: 2⁴⁸⁰/3³⁰⁰=22,804

per x=400 e y=640 si ha: 2⁴⁰⁰/3⁶⁴⁰=64,668

per x=500 e y=800 si ha: 2⁸⁰⁰/3⁵⁰⁰=183,387

per x=600 e y=960 si ha: 2⁹⁶⁰/3⁶⁰⁰=520,047.

Ora verificheremo che questa convergenza verso il basso (che sarebbe stata ancora maggiore prendendo i dati non arrotondati) si verifica soltanto con l'algoritmo che prevede la moltiplicazione per "3" in caso di numero dispari. Se cambiassimo tale parametro dell'algoritmo sostituendo al "3" il "5" avremo:

per x=5 e y=8 si ha: 2⁸/5⁵=0,0819200000

ovvero un valore inferiore a 1, il che significa che l'algoritmo tende a divergere verso l'alto, tendenza ulteriormente accentuata avanzando nelle righe del diagramma come di seguito riportato:

per x=10 e y=16 si ha: 2¹⁶/5¹⁰=0,0067108864

per x=20 e y=32 si ha: 2³²/5²⁰=0,0000450283.

Ancora maggiore sarebbe la divergenza verso l'alto se sostituissimo il "3" con il "7":

per x=5 e y=8 si ha: 2⁸/7⁵=0,0152317486

per x=10 e y=16 si ha: 2¹⁶/7¹⁰=0,0002320061

per x=20 e y=32 si ha: 2³²/7²⁰=0,0000000538.

Per completezza, se sostituissimo il 3 con 1, avremmo una convergenza rapidissima e certa verso la conclusione dell'algoritmo.

Riepilogando, il discrimine tra una convergenza limitata verso il basso e una divergenza illimitata verso l'alto è dato dal numero sopra riportato: 1,61803398749890 che arrotondato a nostro svantaggio a 1,6 e utilizzato per le elevazioni a potenza del 2 e del 3 permette di verificare come le divisioni per 2 spingano a una convergenza verso il basso che le moltiplicazioni per 3 non riescono a contrastare (accade il contrario sostituendo, al 3, parametri dal 5 in su).

Un'obiezione che, a questo punto, si può fare è la seguente: l'analisi finora effettuata è stata fatta sulle righe del diagramma, quindi orizzontalmente, mentre la successione di divisioni per 2 e moltiplicazioni per 3 procede verticalmente.

Per rispondere a tale obiezione, verifichiamo cosa accade nella successione di moltiplicazioni e divisioni a cui viene sottoposto il nostro numero n.

Ricordiamo che l'algoritmo prevede che il numero dispari è sempre seguito da un numero pari, mentre quest'ultimo può essere seguito: o da un numero dispari o da uno o più numeri pari; analizziamo quindi cosa accade mediamente.

Costruiamo qui di seguito le sequenze di pari (P) e dispari (D) facendo in modo che il numero dispari sia seguito alternativamente da uno e da due numeri pari e che, quando è seguito da due pari, a questo faccia seguito alternativamente un dispari o un altro pari (potremmo ulteriormente proseguire alternando, dopo il terzo pari, un dispari e un pari, ma non lo facciamo, sempre a nostro svantaggio).

Le sequenze, limitate ai primi tredici valori di n, sono le seguenti:

Si noti come, pur non tenendo conto degli ulteriori P ai quali abbiamo rinunciato (a nostro svantaggio), il rapporto tra P e D è di 8 a 5, ovvero 1,6 pertanto vale la precedente analisi.

Ricordiamo che oltre alle due ipotesi prese qui in considerazione: divergenza illimitata verso l'alto e convergenza limitata verso il basso, esiste anche l'ipotesi che la successione entri in un ciclo che si ripete senza mai arrivare a 1. Ciò è immediatamente verificabile se, nell'algoritmo, sostituiamo il parametro "3" col "5" (entrando così nel campo dei parametri che danno luogo a divergenza verso l'alto) in questo caso, infatti, è facile trovare due cicli in cui si va a cadere:

13-66-33-166-83-416-208-104-52-26-13

17-86-43-216-108-54-27-136-68-34-17.

Si può notare che entrambi sono formati da dieci numeri e ci si cade quando l'algoritmo parte da uno di questi numeri o ci arriva come valore successivo (ad esempio, partendo da 5 si ottiene subito il 26 e si entra nel primo ciclo, oppure, partendo da 272, si ottiene subito il 136 e si finisce nel secondo ciclo). Considerata l'alta frequenza con cui si entra in un ciclo ripetitivo con il parametro 5 (soltanto nell'intervallo tra n=5 e n=43 ci si entra ben nove volte) se tale eventualità accadesse anche col parametro 3 se ne avrebbe evidenza, cosa che invece non avviene pur essendo arrivati a provare empiricamente la congettura con valori di n che arrivano fino a 5,76×10¹⁸ come provato da Tomás Oliveira e Silva in "The Ultimate Challenge: The 3x+1 Problem" (American Mathematical Society, 2010).