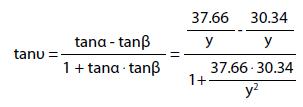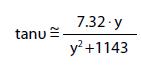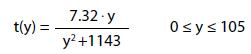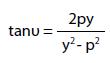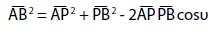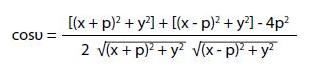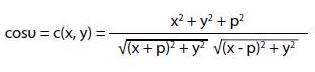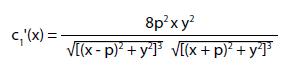Un calcio alla Matematica, ovvero Palanca!!! ...chi era costui?

I Laboratori "Matematica&Realta" (www.matematicaerealta.it) offrono spesso l’occasione per scoprire interessanti e insospettati collegamenti fra la Matematica e la vita quotidiana. Nel corso degli anni, grazie alla collaborazione degli insegnanti responsabili dei laboratori, abbiamo cercato di favorire l’inserimento dei temi M&R nel percorso curriculare. In questa ottica, abbiamo proposto un percorso innovativo sulla Trigonometria. L’argomento ha trovato interessanti interazioni con lo sport, in particolare con il gioco del calcio.

Proponiamo qui il lavoro di approfondimento svolto dai ragazzi dell’Unita locale del Liceo classico "Galluppi" di Catanzaro, coordinati dalla Prof. Anna Maria Canepa. Michela Astorino, Amalia Bonacci, Federica Caporale, Ketty Galiano, Mauro La Manna, Alessandro Lazzaro, Mattia Masciari, Alessandro Nania, Mattia Squillace, Angelica Talarico, Caterina Tucci, Irene Veraldi hanno rispolverato vecchi ricordi presenti nella memoria collettiva di sportivi e tifosi della città e li hanno proposti nel corso del XI Convegno Esperienze a Confronto (Perugia, 27-30 aprile 2009), suscitando curiosità e grande interesse nei partecipanti. Presentiamo qui una rilettura ad uso didattico del lavoro multimediale dei ragazzi¹. Il lavoro originale, con immagini video, e disponibile all’indirizzo http://www.matematicaerealta.it/mediateca/documenti/Galluppiab.rar

Massimo Palanca, il piedino di Biancaneve, il Cruyff dei poveri, approdo a Catanzaro nel 1974 e divenne subito il beniamino dei tifosi e dell’intera città, tanto da essere soprannominato “O RAY”. La sua forza e la sua particolarità erano legate alla capacita di segnare goal dalla bandierina del calcio d’angolo (ne segno ben 13) da dove notoriamente la visuale della porta e nulla.

Anche se i nostri lettori lo troveranno forse inutile, iniziamo − da bravi matematici − con alcune informazioni fondamentali.

Terreno di gioco

Il campo di gioco e di forma rettangolare con misure che possono variare da 45 a 90 metri per il lato minore e da 90 a 120 metri per quello maggiore. Ai quattro angoli del terreno sono fissate le bandierine d’angolo (alte almeno 1,50 m). Un quarto di circonferenza, tracciato con centro sull’angolo e raggio 1 m delimita l’area d’angolo.

Le porte sono posizionate al centro dei lati minori; davanti a ciascuna porta sono tracciati due rettangoli: l’area della porta e l’area di rigore.

Regole del gioco

Nel gioco si affrontano due squadre avversarie di 11 giocatori ciascuna, con l’obiettivo di infilare il pallone nella porta avversaria. Il gioco e soggetto a numerose regole, sotto il controllo di una terna arbitrale. Ad esempio, e concesso effettuare il tiro con i piedi o con la testa ma non con le mani. La porta e difesa dal portiere che e il solo giocatore a poter afferrare il pallone anche con le mani nella sua area. Come tutti i giocatori (anche dilettanti) e i tifosi sanno bene, vari fattori influiscono sul tiro in porta: la velocità del pallone, la distanza dalla porta, la direzione del lancio ecc … Certamente, un fattore chiave e l’angolo di visuale sotto cui il giocatore vede la porta al momento del tiro. A parità di distanza dalla porta, più e grande l’angolo di visuale, più “semplice” sarà centrare la porta e fare goal.

Tiro in porta

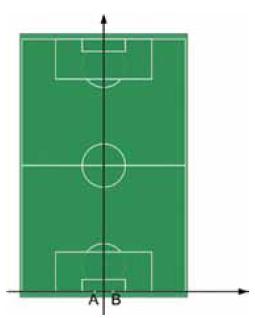
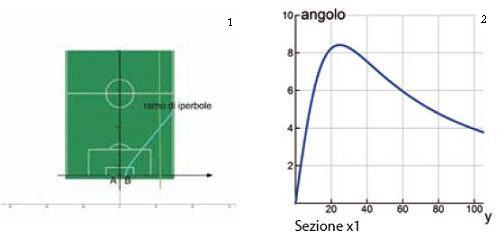
Ci proponiamo di analizzare come varia l’angolo di visuale (della porta) nelle diverse posizioni assunte dal giocatore sul terreno di gioco. Al fine di affrontare la questione in termini matematici, consideriamo un sistema di riferimento cartesiano ortogonale Oxy come in Fig. 1.

Fig. 1

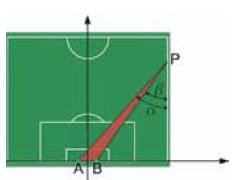
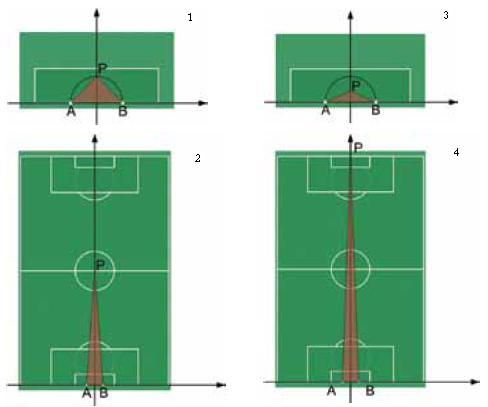
Denotato con AB il segmento che individua la porta e con P la posizione del giocatore, APB = υ è l’angolo di visuale.

Primo caso – linea del fallo laterale

Iniziamo considerando il caso di un giocatore che si trovi in prossimità della linea laterale. Costruzione del modello. Assumiamo che le dimensioni del terreno di gioco siano quelle consigliate dalla FIFA (Tabella 1).

Fig. 2

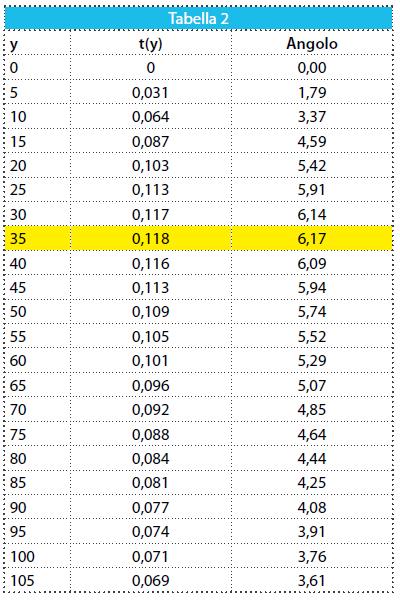
Le coordinate del giocatore sono quindi P = P (34, y), 0 ≤ y ≤ 105 . Se il giocatore si trova presso la bandierina del calcio d’angolo (y = 0) l’angolo di visuale υ è nullo. In ogni altra posizione, lungo la linea del fallo laterale (y > 0), risulta υ = α - β ove α = APQ e β = BPQ . Tenuto conto della risoluzione dei triangoli rettangoli e della formula di sottrazione della tangente, si ottiene:

da cui:

La funzione:

descrive come varia la tangente dell’angolo υ, sotto cui il giocatore vede la porta, in funzione della posizione del giocatore lungo la linea del fallo laterale.

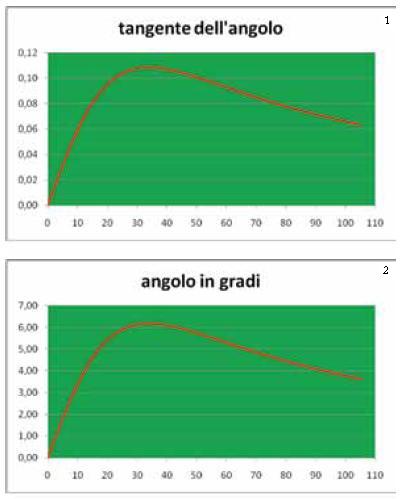
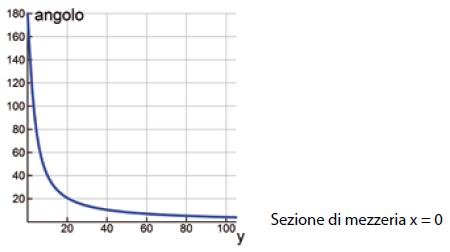
Discussione del modello. Affrontiamo la questione con strumenti elementari. Tabuliamo la funzione t (Tabella 2 – I e II colonna) ed osserviamo il grafico corrispondente (Fig. 3.1). Mentre il giocatore si allontana dalla bandierina del calcio d’angolo lungo la linea del fallo laterale, i valori della funzione t prima crescono, poi decrescono. Evidentemente c’e una posizione nella quale la tangente dell’angolo di visuale e massima. Questa posizione può essere localizzata intorno a 35 metri. In questa posizione anche l’angolo di visione e massimo? Per rispondere alla domanda confrontiamo i valori della tangente con quelli dell’angolo corrispondente (cfr. Tabella 2 – II e III colonna). La tabella e i grafici corrispondenti (cfr. Fig. 3) mostrano chiaramente che al valore massimo assunto dalla tangente corrisponde il massimo angolo.

Fig.3

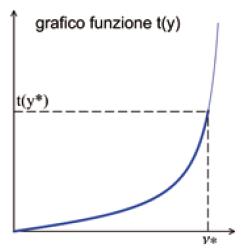
Del resto si poteva giungere alla stessa conclusione osservando il grafico della funzione tangente (cfr. Fig. 4).

Poiché la funzione è crescente, al valore massimo t* = t(υ*) assunto della tangente in un sottointervallo chiuso corrisponde il massimo angolo υ* (Fig. 4).

Fig. 4

Soluzione. Approssimando la posizione ottimale y* = 35 m, si ottiene il valore t (y*) = 0,11839 cui corrisponde un angolo di visuale di circa 6.170: il massimo angolo di visuale è di circa 6.170 e si ottiene intorno a 35m dalla bandierina d'angolo.

Secondo caso – posizione lungo la linea di mezzeria

Passiamo ora a considerare un altro caso, quello in cui il giocatore si trovi lungo la linea di mezzeria del campo. Poiché le dimensioni perimetrali dei campi possono variare, le assumiamo come parametri; precisamente denotiamo con 2ℓ la larghezza e con L la lunghezza del campo. Anche se la larghezza della porta è fissa, per omogeneità la denoteremo con 2p. Approccio geometrico. Con semplici considerazioni geometriche (cfr. Fig. 5.1-5.4) si deduce che l'angolo υ assume valore massimo nel punto medio della porta, formando un angolo piatto. Via via che ci si allontana dalla porta, l'angolo diminuisce fino a raggiungere il suo valore minimo nella mezzeria dell'altra porta. L'angolo da ottuso diventa acuto, toccando i 90° quando il punto P si trova sulla semicirconferenza di centro il punto medio del segmento AB e raggio p (cfr. Fig. 5.2). [Per una nota proprietà di Geometria elementare ogni triangolo inscritto in mezza circonferenza e rettangolo].

Fig. 5

Approccio funzionale. Analogamente a quanto fatto nel primo caso, possiamo valutare la tangente dell'angolo di visione in funzione della distanza dalla porta. In questo caso le coordinate del giocatore sono P = P(0, y), 0 ≤ y ≤ L. Essendo l’angolo di visuale υ = 2APQ, tenuto conto della risoluzione dei triangolo rettangoli e della formula di duplicazione della tangente, si ottiene:

Fig. 6

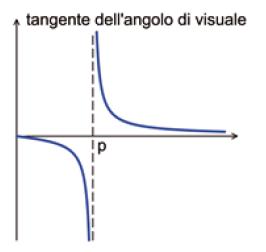
Discussione del modello. La funzione che abbiamo ottenuto non è definita per y = p. Del resto, come abbiamo già osservato, per y = p l'angolo di visuale è retto e, come è noto, la tangente presenta un asintoto verticale in corrispondenza a tale angolo (cfr. Fig.6). Il modello non è quindi adatto allo scopo che ci siamo prefisso ed occorre modificarlo. Affronteremo la questione nel caso generale.

Terzo caso – posizione generica

Consideriamo il tiro in porta da un qualsiasi punto del terreno di gioco.

Costruzione del modello. Denotato con P = P (x, y) la posizione del giocatore, l'ascissa x varia nell'intervallo [- ℓ, ℓ] , mentre l'ordinata y e vincolata in [0,L] .

Fig. 7

Poiché, come abbiamo visto nel punto precedente, la funzione tangente non si rivela adatta a descrivere angoli che passano con continuità da acuto ad ottuso, occorre cambiare funzione trigonometrica. Fra quelle elementari, la funzione coseno e l'unica ad essere biunivoca per angoli che variano da 0° a 180°, come nel caso di nostro interesse. Proviamo allora a descrivere l'angolo di visione mediante il suo coseno.

La Fig. 7 evidenzia che il triangolo APB è in generale scaleno. Applicando il teorema di Carnot, abbiamo:

da cui si ottiene:

La funzione:

descrive come varia il coseno dell’angolo υ sotto cui il giocatore vede la porta.

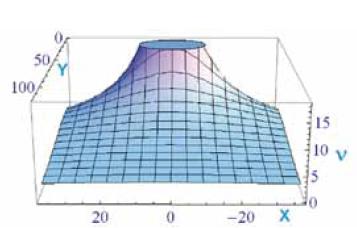
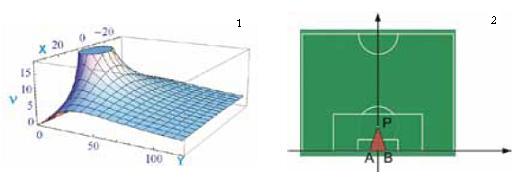
Discussione del modello. Approccio soft. La precedente funzione coseno non e definita nei punti P(±p, 0), ovvero sui pali della porta, ove l'angolo di visuale e indefinito. Si tratta di una funzione di due variabili il cui grafico (tracciato con l’aiuto di un software) e riportato in Fig. 8.

Fig. 8

Il grafico mostra un’evidente simmetria rispetto all'asse delle ordinate. Inoltre, in ogni sezione trasversale (y = costante), la posizione di massima visuale e nel punto di mezzeria del campo, come e naturale aspettarsi. In altri termini, le posizioni migliori giacciono sull’asse della porta x = 0.

Approccio hard. Possiamo verificare questa congettura con gli strumenti del calcolo infinitesimale. Sezioni trasversali. Fissata la variabile y (considerata come parametro), discutiamo come varia la funzione c1(x) = c(x,y) con -ℓ ≤ x ≤ ℓ.

Adottando l’usuale metodo del segno della derivata

essendo c1'(x) < 0 per ogni -ℓ < x < 0 e c1'(x) > 0 per ogni 0 < x < ℓ, si deduce che x = 0 e il punto di minimo della funzione c1.

Soluzione. Poiché la funzione coseno e monotona decrescente in [0,180], al valore minimo del coseno corrisponde un angolo massimo (Fig. 9, Fig. 11), associato alla posizione ottimale sulla mezzeria.

FIGURE

Sezioni longitudinali. Passiamo ora a studiare le sezioni longitudinali ovvero fissata la variabile x (considerata come parametro), discutiamo come varia la funzione c2(y) = c(x, y) con 0 ≤ y ≤ L.

Adottando l’usuale metodo del segno della derivata, abbiamo:

FORMULA

Risulta c2'(x) > 0 se e solo se p2 - x2 + y2 > 0.

Soluzione. Discutiamo la disequazione e interpretiamo il risultato. Consideriamo prima il caso |x| < p ovvero il caso in cui il giocatore si muove lungo una sezione longitudinale compresa fra i pali. Risulta c2'(x) > 0 per ogni y > 0. Quindi la funzione c2 assume valore minimo (pari a -1) in y = 0, cui corrisponde un angolo di visuale massimo di 180° (cfr. Fig. 12).

Fig. 12

Si osservi che questo risultato estende e conferma quanto trovato per via geometrica lungo la sezione (longitudinale) mezzeria della porta. Se |x| = p allora c2'(x) > 0 per ogni y > 0. Di conseguenza la funzione c2(y) e crescente lungo tali sezioni (si può agevolmente provare, ricorrendo al processo di limite, che l'angolo limite massimo e retto).

Assumiamo infine |x|>p, ovvero che il giocatore si muova lungo una sezione longitudinale

esterna ai pali. Risulta c2'(x) > 0 per ogni y > √(x2 - p2) e c2'(y) < 0 per ogni 0 < y < √(x2 - p2) .La funzione c2 assume quindi valore minimo nel punto ove il ramo di iperbole y = √(x2 - p2) interseca la sezione stessa [cfr. Fig. 13.1], cui corrisponde un angolo di visuale massimo [cfr. Fig . 13.2].

Fig. 13

Il valore massimo dell'angolo di visuale naturalmente dipende dalla sezione longitudinale, come si evince anche dal grafico 3D in figura 14.1. Il risultato estende quanto trovato lungo la sezione del fallo laterale attraverso la funzione tangente. Determiniamo il valore dell’ angolo di visuale nel caso particolare del calcio di rigore (Fig. 14.2).

Fig. 14

Posto P(0,11), risulta cos υ=c(0,11) = 0.80 cui corrisponde un angolo υ=36.80°.

Calcio di rigore (Penalty)

Punizione assegnata contro la squadra che commette un fallo passibile di calcio di punizione diretto nella propria area di rigore. Può essere calciato direttamente in porta posizionando il pallone sul dischetto del rigore posto a undici metri di distanza dalla porta senza ostacolo di difensori, a parte il portiere. (www.wikipedia.it).

Conclusioni. Alla luce di quanto sin qui analizzato appare irrisolto un enigma: come ha fatto Palanca a segnare da un punto in cui la visuale e nulla? e stata magia?

La realtà sembra dimostrare l'inadeguatezza della Matematica! In realtà, la Matematica e in grado di spiegare anche il miracolo di Palanca ... ma occorre un modello più sofisticato. Il pallone nel suo moto descrive una parabola, che si riduce ad un segmento nel caso di un tiro radente al campo di gioco. In generale comunque giace in un piano. Nel caso del tiro a effetto, ovvero quando si imprime una rapida rotazione su se stesso al pallone, la traiettoria può diventare fortemente sghemba (non complanare). Con un tiro ad effetto si può segnare anche dalla bandierina del calcio d'angolo, sebbene da tale posizione lo specchio della porta e nullo! Naturalmente ci vuole una grande maestria per controllare la traiettoria del pallone in un tiro a effetto, ma questo e il merito dei grandi ...

Massimo Palanca in campo

1. Gli autori ringraziano i ragazzi che, con entusiasmo e curiosità, hanno partecipato al laboratorio stimolati dall'interesse per la Matematica.

Bibliografia

1] P. Brandi, A. Salvadori, Prima di iniziare, Conoscenze e competenze matematiche di base per l’Universita, www.Aquaplano.eu, 2010

2] P. Brandi, A. Salvadori, Matematica&Realta, Percorso D – Fenomeni e funzioni periodici, 2010