Una nuova edizione per il "Furor Mathematicus"

Aspettavamo da decenni questo momento: la pubblicazione del Furor Mathematicus di Leonardo Sinisgalli. Finalmente è arrivato! Dal giorno 8 ottobre Mondadori ripropone il libro come ristampa dell'edizione del 1950 che uscì ad opera della stessa casa editrice. Non è la prima pubblicazione, c'era già stata un'edizione del 1944 ma non così completa come quella uscita sei anni dopo, motivo che ha indotto i curatori a scegliere la successiva.

Il Furor è un lavoro particolare, premonitore e completo al tempo stesso. Ci piace dire che è il suo testamento culturale: in esso ci sono il pensiero, la poetica e i contenuti di tutto quello che Leonardo Sinisgalli ha già fatto fino a quel momento e di tutto quello che farà successivamente.

L'opera contiene una raccolta di scritti, spesso autobiografici, saggi, brevi dialoghi, corrispondenza personale, poesie e riflessioni sugli argomenti più diversi; si parla di matematica (la passione di sempre di Sinisgalli), fisica, poesia (il suo grande amore), letteratura, pittura, architettura, tecnologia, design, ecc. Non ci sono barriere tra i diversi argomenti, in ognuno si percepisce che le diverse discipline comunicano tra loro e per far questo sono in grado di capirsi e di confrontarsi.

Emblematica, in questa direzione, l'affermazione di Sinisgalli tratta da un articolo dal titolo Natura calcoli e fantasia, comparso sulla rivista Pirelli nel 1951:

"[…] La Scienza e la Tecnica ci offrono ogni giorno nuovi ideogrammi, nuovi simboli, ai quali non possiamo rimanere estranei o indifferenti, senza il rischio di una mummificazione o di una fossilizzazione totale della nostra coscienza e della nostra vita. […] L'Arte deve conservare il controllo della verità, e la verità dei nostri tempi è di una qualità sottile, è una verità che è di natura sfuggente, probabile più che certa, una verità "al limite", che sconfina nelle ragioni ultime, dove il calcolo serve fino a un certo punto e soccorre una illuminazione; una folgorazione improvvisa. Scienza e Poesia non possono camminare su strade divergenti. I Poeti non devono aver sospetto di contaminazione".

Come già detto Sinisgalli cerca sempre un legame tra le varie conoscenze e tutti i suoi scritti sono pervasi da questo obiettivo; in particolare la Matematica penetra e attraversa le altre conoscenze e da esse, a sua volta, è attraversata. In effetti tutta la formazione di Sinisgalli si è alternata tra due grandi attrazioni, da una parte la conoscenza scientifica (dopo due anni trascorsi alla facoltà di Matematica passa a Ingegneria e si laurea in Ingegneria aerospaziale), dall'altra la passione per la Poesia (ambito nel quale ottiene anche importanti premi e riconoscimenti).

Indiscutibile la sua creatività e la grande professionalità nel design e nella comunicazione, non a caso è stato il fondatore e art director delle più importanti riviste industriali italiane tra le quali ricordiamo la rivista Pirelli (1948-1952) e Civiltà delle macchine (1953-1958). Da non dimenticare che questi sono gli anni della rinascita dell'Italia; la nazione, appena uscita dalla guerra, affronta una trasformazione incredibile: quella che da paese agricolo la fa diventare un paese industriale. Comincia l'era del boom economico!

Il Furor Mathematicus contiene sei sezioni e due inserti stampati su pagine verdi (nella edizione recente sono grigie). Poniamo la nostra attenzione su due di queste in particolare. La prima sezione - che ha lo stesso titolo del libro - inizia con Quaderno di geometria, uno scritto di poche pagine che, come G.I. Bischi e L. Curcio affermano in La Matematica secondo Sinisgalli:

"fu scritto da Sinisgalli nel 1935 a Montemurro in un momento di pausa e di riflessione dopo la prima stagione milanese. In questa opera Sinisgalli offre al lettore, ancora una volta, il connubio tra i vari saperi e mette in mostra tutte le sue conoscenze matematiche collegando tra loro contenuti altamente raffinati dei quali parla con estrema semplicità. In realtà in questo piccolo lavoro c'è molto di più: la chiarezza e la sintesi ne fanno un vero emblema, che sarà, non a caso, un biglietto di presentazione e di ingresso alla Olivetti".

Al Quaderno di Geometria Sinisgalli si ispirerà per ricavare i testi e la sceneggiatura del documentario scientifico Lezione di Geometria dedicato ai modelli di gesso, di cartone, di filo conservati nella collezione del Seminario di matematica presso l'Università di Roma, forme affascinanti di quella Geometria che Sinisgalli definisce "Barocca" e che spesso si ritrovano in natura nelle forme della crescita animale e vegetale. Il cortometraggio, prodotto da Carlo Ponti, per la regia di Virgilio Sabel, la fotografia di Mario Bava, e le musiche di Goffredo Petrassi, vinse nel 1949 il Leone d'Argento alla Mostra cinematografica di Venezia per il miglior documentario.

Ritorniamo a Quaderno di Geometria dove in poche pagine Sinisgalli descrive il percorso e i contenuti della matematica dall'antichità fino ai concetti più moderni con indiscutibile precisione, semplicità e chiarezza; lo scritto inizia con una lunga citazione, in francese, dei Canti di Maldoror di Lautréamont, pseudonimo di Isidore Lucien Ducasse (1846-1869), un inno d'amore per la disciplina:

O matematiche severe, io non vi ho dimenticato sin da quando le vostre sapienti lezioni, più dolci del miele, filtrarono nel mio cuore e mi rinfrescarono. Fin dalla culla chiesi di bere alla vostra sorgente [...].

Sempre in Quaderno di Geometria si può ammirare la padronanza e la semplicità con la quale Sinisgalli parla di argomenti matematici non semplicissimi quali i numeri complessi descrivendoli come trasformazioni, l'approccio più semplice e immediato. E ancor più lo straordinario tentativo di legare tra loro concetti contemplati da discipline a dir poco lontane tra di loro, come si legge nella quarta sezione dal titolo Corrispondenze in una delle lettere che Sinisgalli scrive a Gianfranco Contini:

Carissimo Gianfranco

cerca di approfondire questa idea che mi sono fatto della poesia: un quantum, una forza, una estrema animazione esprimibile mediante un numero complesso a+bj: idealis mundi monstrum, inter ens et non ens amphibium (Leibniz); una quantità silvestre (Cardano); somma di un reale e di un immaginario (Cartesio); un vettore diremmo noi con Marcolongo. Tu sai che l'insieme più vasto dei numeri pensabili è quello dei numeri complessi: con questi numeri non un punto segnato sopra un piano resta indeterminato. […] Ma torniamo ai numeri complessi e alla poesia, al binomio a+bj, dove a e b sono quantità reali e j è il famoso operatore immaginario. Questo operatore dà un senso, un'inclinazione al numero che per sua natura è orizzontale e inerte, lo rende attivo, lo traduce in una forza. A me pare analoga l'azione di j a quella che il poeta esercita sulla "cosa". Le parole per formare un verso devono avere una particolare inclinazione (scritta così questa frase sembra addirittura lapalissiana). Voglio dire, insomma, che il simbolo j ci darebbe un'idea di quella che è l'alterazione provocata dal linguaggio sulla realtà, del rapporto cioè tra "cosa" e "immagine".

Nella prima sezione dedicata fondamentalmente alla matematica, alla tecnologia, alle macchine e agli automi, Sinisgalli non manca di omaggiare i suoi maestri, si legge di loro in Carciopholus Romanus dove li ricorda mentre ammirano e discutono la forma della superficie geometrica detta Romana di Steiner:

Il prof. Conforti, il prof. Severi, e il prof. Fantappiè, tre luminari, — Severi alto e ricciuto, Fantappiè tondo e piccolo, Conforti magro e mezzano, — che erano vicini a me, a guardare quella forma, sembravano commossi, commossi… «Questa superficie» io dicevo «è un frutto romano, come il carciofo». Ma Severi, Conforti e Fantappiè ne enumeravano invece tutte le mirifiche proprietà: 4 cerchi generatori, tre poli tripli, un'area calcolabile per integrali razionali, e poi non so che altre diavolerie.

Sempre in questa sezione l'autore dedica un capitolo a Leonardo da Vinci, il suo mentore, per lui una continua fonte di ispirazione e di conoscenza e racconta anche del cambio di rotta nei suoi studi e nei suoi interessi e l'inizio del suo amore per la Poesia e per la vita dei poeti.

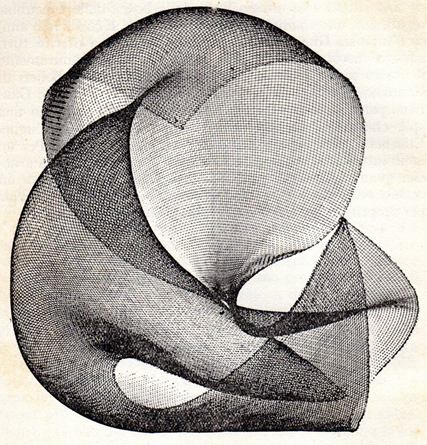
CONCAVO-CONVESSO 1948 di Bruno Munari (Plastico di rete di ottone)

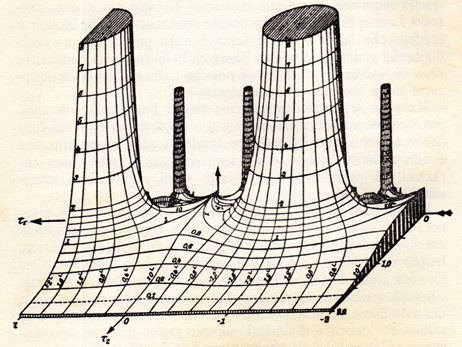
LE TORRI ASTRUSE (Rappresentazione di una superficie a variabili complesse)

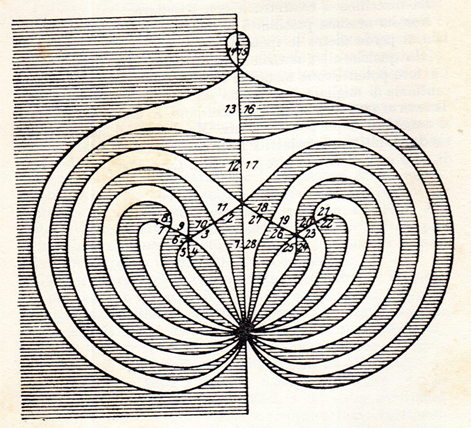
LABIRINTO MATEMATICO

La seconda sezione del Furor dal titolo Promenades Architecturales è dedicata a Adriano Olivetti; in questa Sinisgalli propone una lunga riflessione sull'Architettura nella quale ricorda anche i suoi amici che non c'erano più: Edoardo Persico, Guido Modiano, Paolo Masera. In particolare è a Edoardo Persico e ai suoi insegnamenti e ai suoi pensieri sulla crisi dell'Architettura che dedica un capitolo della sezione:

A circa dieci anni di distanza dalla sua morte ci tornano in mente le sue parole. Persico non era un esteta, era qualcosa di più di un Apollinaire italiano, era un uomo della tempra di Gobetti e di Gramsci. Egli soffrì e capì più di tutti noi, che allora eravamo soltanto ragazzi, la grande crisi dell'architettura come un sintomo di una incertezza più grave e oscura che pesava sulla nostra sorte…

[…]

Persico che a noi emigranti offri asilo e aiuto, ma soprattutto la speranza di poter lassù mettere alla prova qualcosa che avesse più valore della nostra intelligenza, non la pigra capacità di scrivere una buona pagina, ma la attiva e affettuosa collaborazione con gli uomini: tipografi, vetrai, disegnatori, architetti, industriali. Persico presentandoci degli artigiani come Lucini, come Nizzoli, come Buffoni (anziché le eminenze della città: Padre Gemelli, Mattioli, e la signora Ruskaja), sapeva di farci un dono che ci avrebbe giovato per tutta la vita, sapeva di allargare la nostra educazione nell'unico senso veramente utile. Così il miraggio dell'architettura significò per noi tante cose, ma, più che un problema di stile, la possibilità di adeguare la vita nostra, le nostre aspirazioni, le nostre virtù, a quelle di tutti gli uomini.

MAIUSCOLA ORNATA di G. B. Piranesi

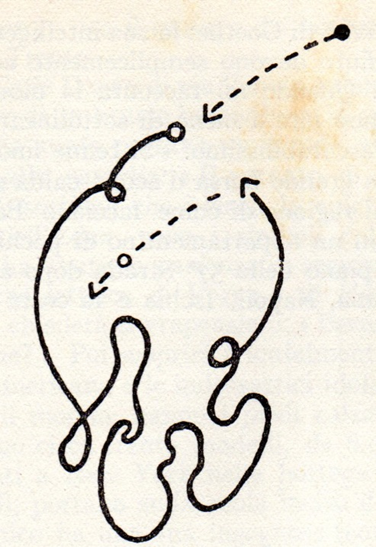
PRELUDIO N. 3 di Chopin, I° tempo (Tracciato dei movimenti della danza)

DUE CIGI di A. Steffen (Tracciato dei movimenti dei due danzatori)

Negli inserti con le pagine verdi incontriamo piccoli gioielli, quasi gemme in un prato, su pensieri e argomenti diversi; in uno di questi dal titolo Sfera leggiamo alcune righe:

… La sfera è una forma che presenta lo stesso margine comunque cambi il punto di vista. Essa è protesa in tutte le direzioni senza alcuna preferenza, e non lascia che una sola possibilità di appiglio a una superficie piatta: toccarla in un punto. Nella sfera ogni punto è ugualmente prezioso ed ugualmente trascurabile, è un punto qualunque della sfera, privo di ogni singolarità. Tutti gli spostamenti la ritrovano identica negli infiniti piani di simmetria, nell'unica faccia che ne nasconde la perfezione. Non saprà mai piegarsi da un lato o dall'altro. Non sa negare, non sa consentire: anche quando sembra sporgersi, riflettere, cadere…

Il linguaggio geometrico, che descrive le proprietà geometriche, si trasforma in un linguaggio universale, simbolico e estremamente significativo in qualsiasi ambito lo si voglia tradurre e interpretare. La Geometria diventa monito, messaggio di uguaglianza e di dignità.

Questo il lavoro stupendo di Leonardo Sinisgalli, che 69 anni dopo viene riproposto. La nuova edizione, fortemente voluta dalla Fondazione Leonardo Sinisgalli, si apre con una interessante introduzione di Gian Italo Bischi dell'Università di Urbino che ne sottolinea l'attualità seppure nel cambiamento del contesto: l'Italia di oggi non è l'Italia del 1950! "Oggi - scrive Bischi - siamo di nuovo in un momento di grande transizione, questa volta verso un'economia e una società della conoscenza e dell'informazione, in cui più che macchine e produzioni materiali, quantità di materie prime e forza lavoro, diventano importanti la qualità del sapere e l'innovazione, la conoscenza e la capacità di elaborare dati per estrarne informazioni. Nuovi profili professionali si creano, sempre più legati a qualità e quantità della conoscenza, capacità di aggiornarsi mediante formazione continua e globale, adattamento dei saperi a nuove situazioni…"

Dopo aver espresso perplessità sul fatto che forse oggi l'Italia non è pronta all'appuntamento, Bischi sottolinea, tra le varie letture e interpretazioni che si possono dare del Furor, una diversa possibilità, un filo conduttore individuabile nel sogno; afferma infatti che la "forza propulsiva di ogni cambiamento, la capacità di sognare, non può che basarsi sulla sovrapposizione, sull'incrocio di saperi; insegnamento ancora attuale che il Furor può trasmettere in questo complesso momento di transizione verso la società della conoscenza e dell'innovazione".

Noi ci auguriamo che tutte le idee e le riflessioni proposte nel Furor inducano gli studenti e i loro docenti a leggerlo, a discuterlo e commentarlo e ovviamente anche a criticarlo; è talmente forte e fondante il principio che ispira questo libro che l'aspetto formativo della sua conoscenza è indiscutibile.

Buona lettura a tutti!