Curve e curvature: parte prima
Alcune proprietà locali delle curve piane
Rappresentazione parametrica della retta
Rappresentazione parametrica della retta
1. La retta
Iniziamo con l'ottenere la rappresentazione parametrica di una retta che, evidentemente, possiamo ritenere la curva piu semplice. A tal fine utilizzeremo il concetto di vettori paralleli (detti anche collineari), concetto che afferma il parallelismo di due vettori u e v se e solo se l'uno si può esprimere come la moltiplicazione di uno scalare t per l'altro ossia v=t u.
Siano quindi
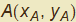
e
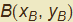
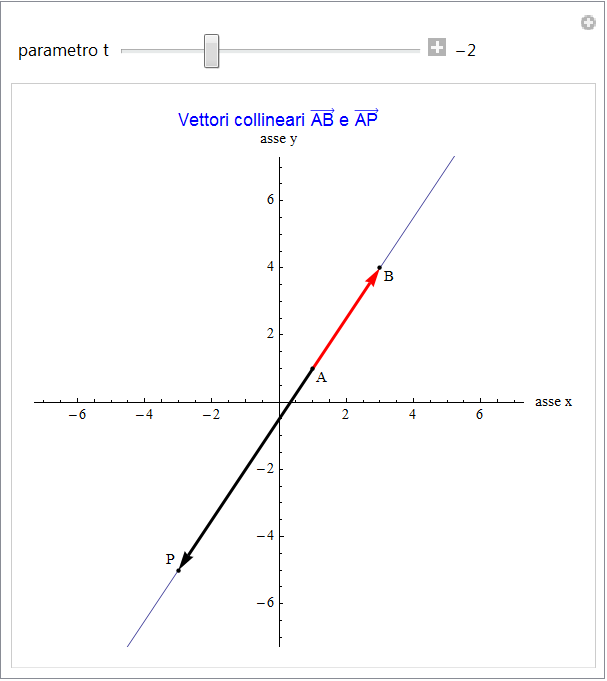
due punti del piano cartesiano distinti. Per essi passa una sola retta r e inoltre definiscono il vettore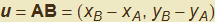 
. Un punto qualsiasi P(x, y) apparterrà ad r (fig. 1) se il vettore 
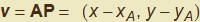è parallelo o collineare a u ossia v=t u, relazione che si esplicita in termini delle componenti:
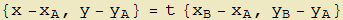
o anche nel sistema:
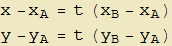
cioè:
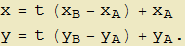
figura 1
Abbiamo in tal modo ottenuto la rappresentazione parametrica della retta passante per i due punti dati (fig. 1). Quest'ultima mostra una dipendenza lineare delle coordinate del punto P dal parametro reale t i cui coefficienti forniscono le componenti del vettore AB mentre i termini noti sono le coordinate di uno dei due punti (nell'esempio, A). Viceversa, partendo dalla coppia di equazioni lineari:
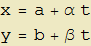 | (1) |
associamo al punto P(x, y) il vettore OP (avente l'estremo iniziale nell'origine O di un sistema cartesiano), al punto di coordinate A(a, b) il vettore OA = v = (a, b) e ai coefficienti di t il vettore u = (α, β). La coppia di equazioni (1) si può ora riscrivere come:
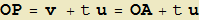
da cui:
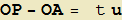
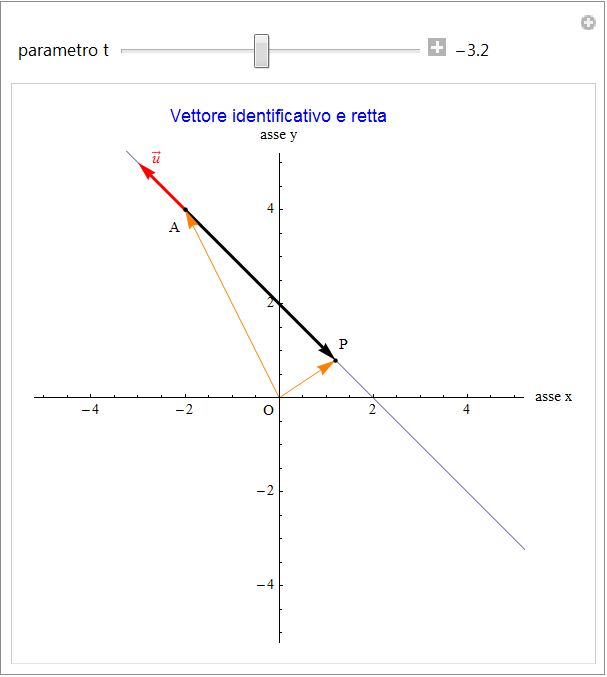
cioè ancora una relazione di collinearità tra il vettore costante u (che quindi individua una particolare direzione) e quello con estremo variabile OP - OA = OP + AO = AP (figura 2).
In definitiva, la retta r si può esprimere tramite una funzione vettoriale lineare del parametro t del tipo:
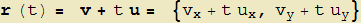
con u vettore che definisce la direzione e v che invece identifica un suo punto.
figura 2
2. Vettore perpendicolare
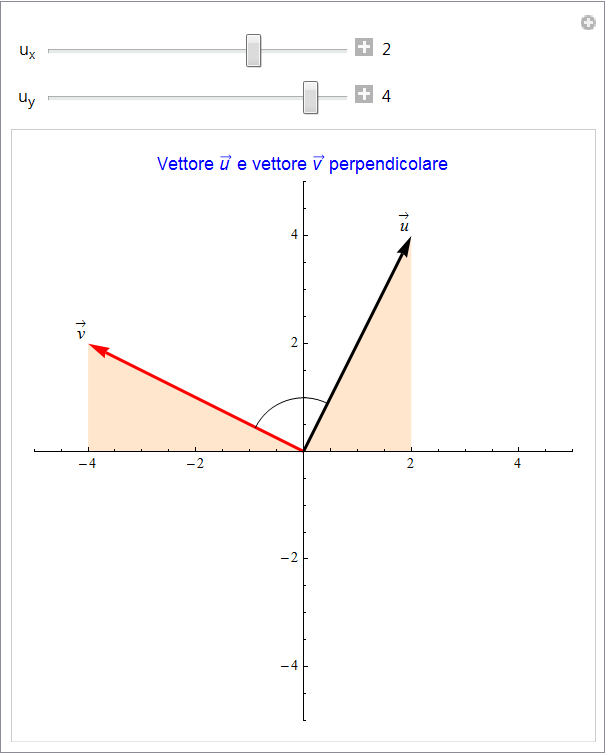
Dato il vettore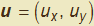 
, vogliamo associargli un vettore perpendicolare. Per far ciò, è sufficiente tener presente che due vettori non nulli sono perpendicolari se e solo se il loro prodotto scalare è nullo. Pertanto posto 
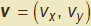la condizione:
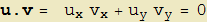
sarà soddisfatta se, tra le varie possibilità, poniamo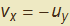 
e 
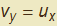. Il vettore 
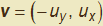risulta quindi perpendicolare ad u. Si può facilmente verificare che si ottiene da quello iniziale con una rotazione antioraria di 90° con l'animazione seguente (fig. 3) dove si potranno variare le componenti del vettore u.
figura 3
Infine, se abbiamo una retta espressa dalle (1) caratterizzata dal vettore u = (α, β) e passante per A(a, b), la retta per A a essa perpendicolare (figura 4) sarà rappresentata dalle equazioni:
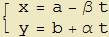 | (2) |
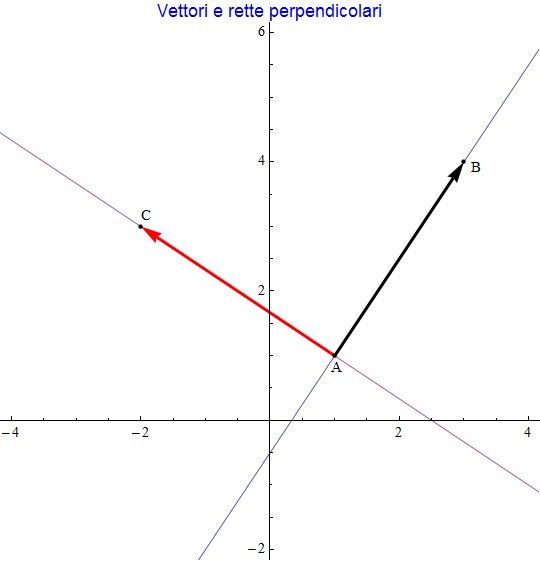
figura 4
Curve e vettore tangente3. Rappresentazione di una curva
Nella sezione precedente, abbiamo visto come le coordinate di un punto generico su una retta si possano rappresentare tramite due funzioni dipendenti linearmente da un parametro. Possiamo pure pensare (le animazioni proposte confortano tale idea) la retta come un particolare luogo che viene percorso da un punto che si muove nel piano ossia, con termini mutuati dalla Fisica, come una particolare traiettoria seguita da un punto in moto. In tal caso, il parametro rappresenta la grandezza fisica tempo.
Queste osservazioni si possono generalizzare: possiamo pensare di descrivere l'insieme di punti caratterizzanti una curva nel piano tramite una coppia di funzioni, entrambe dipendenti da un parametro e tali da rappresentare rispettivamente l'ascissa e l'ordinata di un punto in un sistema cartesiano. Se al parametro associamo intuitivamente un istante temporale t, la curva che emerge si potrà considerare come la traiettoria seguita da un punto in moto.
Pertanto nel seguito considereremo assegnata una curva γ quando siano date le due funzioni:
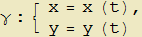 | (3) |
dove t rappresenta un parametro reale variabile nell'insieme I (t ∈ I e I ⊆ R) e x e y le coordinate di un punto P(x, y) ∈ γ in un sistema cartesiano. Se O è l'origine del sistema cartesiano con assi definiti dai versori canonici i e j, la coppia di funzioni (3) si può pure interpretare come le componenti del vettore posizione del punto P, r = OP, nell'istante t:
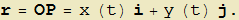
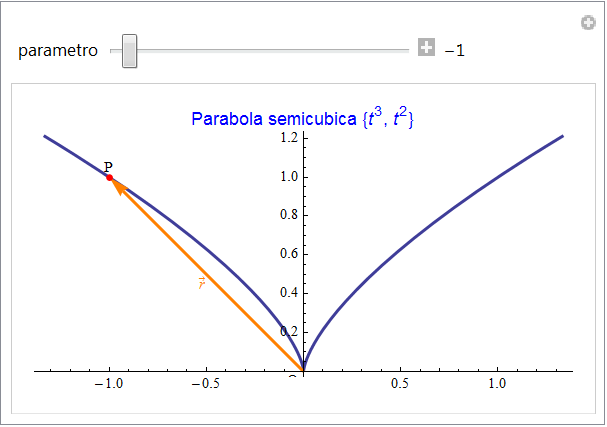
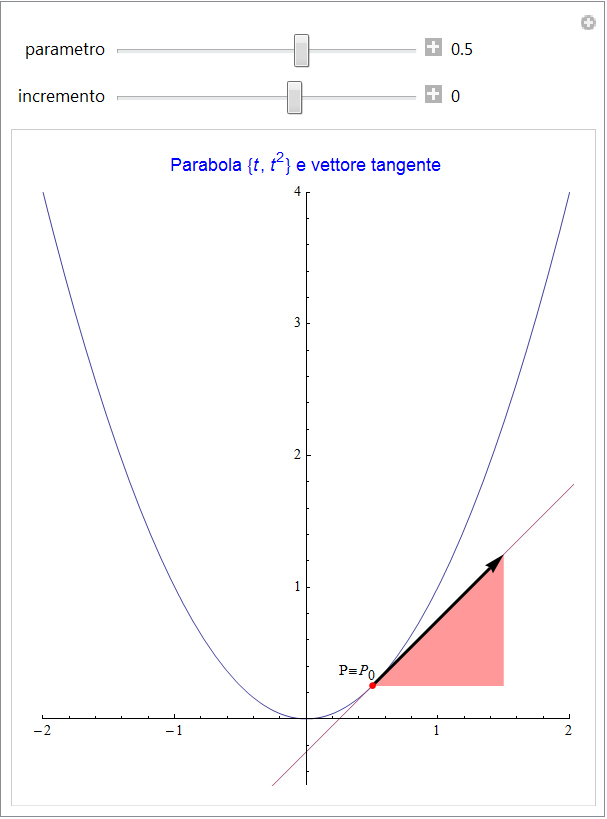
Abbiamo, in sostanza, la cosiddetta rappresentazione parametrica di una curva. Quale esempio, nella figura 5 viene rappresentata la curva espressa dalla coppia di funzioni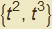 
e il vettore che identifica un suo punto generico (variabile nell'animazione associata alla figura).
figura 5
4. Vettore tangente
In questa sezione vedremo come sia possibile assegnare a ogni punto di una (opportuna) curva espressa in forma parametrica il vettore tangente. La metodologia ricalca quella presente in tutti i manuali scolastici a proposito del significato geometrico di derivata di una funzione data nella forma y = f(x) anche se qui ne generalizza il risultato alla rappresentazione parametrica. Sia quindi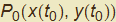 
un punto di una curva γ data dalle funzioni γ : {x(t), y(t)} e sia h un incremento del parametro t cui corrisponde su γ il punto 
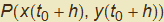. Possiamo ora associare a questi due punti il vettore 
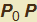avente per componenti:
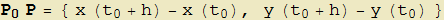
Se la moltiplichiamo per lo scalare 1/h, otteniamo un vettore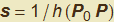 
ancora con la medesima direzione di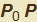 
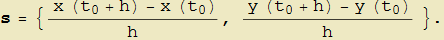
Quest'ultimo caratterizza geometricamente la direzione della retta secante la curva γ e passante per i punti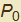 
e P (nella figura 6, questo vettore è rappresentato in corrispondenza di un incremento h ≠ 0). Le componenti di tale vettore sono il rapporto incrementale di ciascuna funzione rappresentativa di γ. Se, al tendere allo zero dell'incremento i limiti di questi rapporti incrementali esistono finiti, si pone:
essendo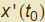 
e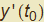 
le derivate delle due funzioni di γ calcolate in 
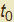. È noto che in tale processo la retta secante (e quindi pure il vettore s) tende ad assumere la direzione della retta tangente per cui si giustifica la definizione di vettore tangente t nel punto P(x(t), y(t)) come quel vettore le cui componenti siano espresse da:
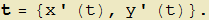 | (4) |
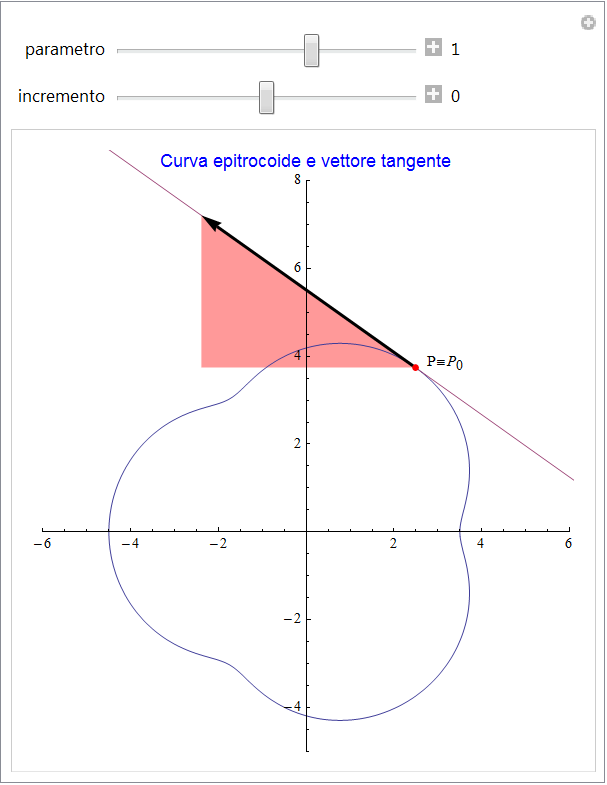
Le animazioni seguenti (figg. 6 e 7) mostrano la situazione dal punto di vista geometrico: se h ≠ 0 appare il vettore secante s con in colore il triangolo delle sue componenti mentre, se si pone h = 0 (che è la situazione iniziale), appare rappresentato il vettore tangente.
figura 6
figura 7
5. Versore tangente
In entrambe le figure 6 e 7 precedenti appare evidente come il vettore tangente vari da punto a punto sia in direzione che nel suo modulo. Volendo individuare caratteristiche intrinseche delle curve indipendenti dalla loro particolare rappresentazione, ci chiediamo se questa variabilità sia appunto una caratteristica intrinseca della curva o se dipenda dalla particolare parametrizzazione scelta. A tal fine riprendiamo la semplice parametrizzazione della parabola utilizzata nella figura 6,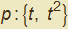 
, e sostituiamo al parametro t il parametro - t cioè 
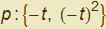. Evidentemente la curva rimane la stessa (eliminando il parametro si giunge comunque all'equazione conosciuta 
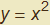) ma appare altrettanto evidente (figura 8) che tale trasformazione non fa altro che invertire il verso del vettore tangente. Si passa da t = (1, 2t) a t' = (-1, 2t) per cui, per esempio, nel punto A(1, 1) corrispondente a t = 1 nella prima rappresentazione, il vettore tangente ha componenti 
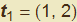mentre nella seconda rappresentazione (dove è t = -1) abbiamo 
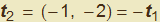. I due vettori hanno, come aspettato, ancora la medesima direzione ma verso opposto.
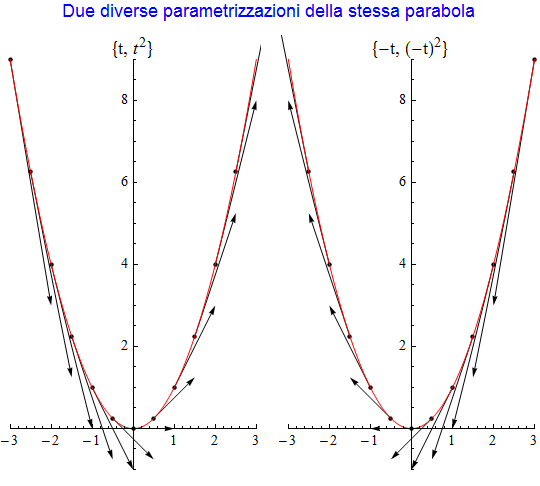
figura 8
Se consideriamo la curva in questione come la traiettoria di un punto in moto, potremo dire che il vettore tangente dipende quindi dal verso di percorrenza del punto sulla curva. Tutto ciò appare naturale e coerente con la classica interpretazione fisica di una curva intesa come traiettoria di un corpo in moto e dove si associa al vettore tangente il vettore velocità.
Passando ad una terza rappresentazione parametrica della medesima parabola data da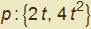 
, otteniamo che il vettore tangente è dato da 
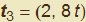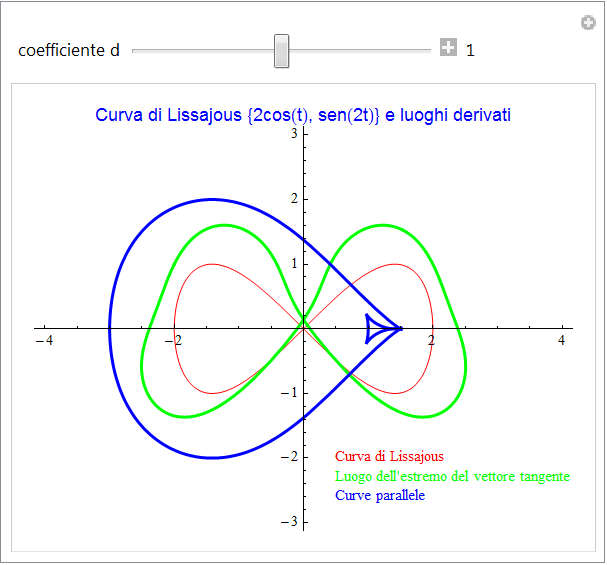
per cui cambia, in tal caso, pure il suo modulo. Difatti, considerando sempre il medesimo punto A corrispondente questa volta a t = 1/2, risulta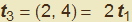 
il cui modulo è diverso dal precedente pur mantenendo la medesima direzione. Un ulteriore esempio con una delle più semplici figure di Lissajous conferma ancora queste osservazioni (figura 9).
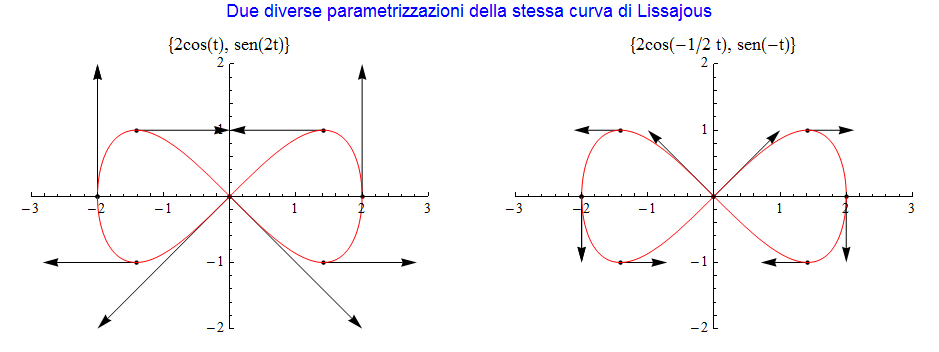
figura 9
Concludiamo sostenendo che l'unica caratteristica intrinseca della curva espressa dal vettore tangente è la sua direzione mentre modulo e verso dipendono dalla particolare parametrizzazione.
Siamo quindi giunti ad un primo importante risultato: da questo punto in poi, sarà il versore tangente l'elemento che verrà associato a (quasi) ogni punto della curva in quanto, una volta che si sia scelto uno dei due possibili versi di percorrenza, esso è indipendente dalla rappresentazione scelta. Se quindi la curva γ è data dalle γ : {x(t), y(t)}, il versore tangente associato localmente al punto corrispondente al valore t del parametro risulta
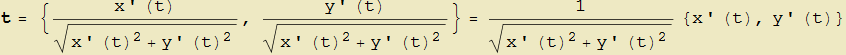 | (5) |
ottenuto dividendo le componenti del vettore tangente espresso dalle (4) per il suo modulo (figura 10). Perché ciò sia possibile, devono essere evidentemente soddisfatte le condizioni
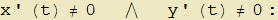
pertanto, in quanto segue, ci limiteremo a quelle curve che le rispettano e che per tale motivo vengono dette regolari.
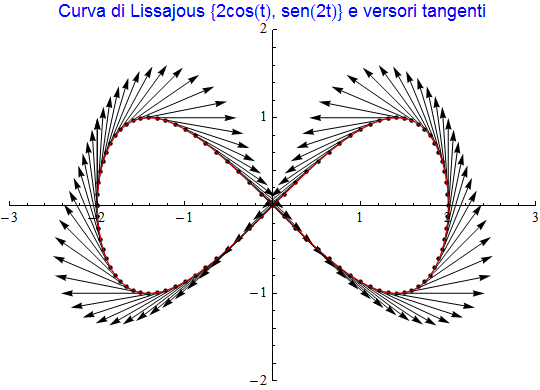
figura 10
6. Curiosità
L'ultima immagine (fig. 10) ci suggerisce il modo di costruire ulteriori curve a partire da quelle date. Difatti, siccome il versore tangente associa a un punto della curva data (che è pure il suo estremo iniziale) un secondo punto che costituisce l'altra sua estremità, potremo studiare il luogo di questi ultimi punti. Se poi sostituiamo al versore tangente il versore normale:
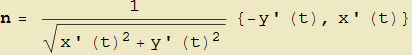 | (6) |
la curva descritta dall'estremo finale del versore normale (fig. 11) è un caso particolare di curva parallela ossia di curve che mantengono una distanza costante "d" dalla data curva. Così, se moltiplichiamo tali versori per lo scalare d, il vettore che ne deriva avrà modulo pari a |d| e potremo visualizzare le curve che si ottengono al variare di tale parametro. L'animazione di fig. 12 realizza uqesto procedimento a partire dalla curva di Lissajous precedente e con d = 1.
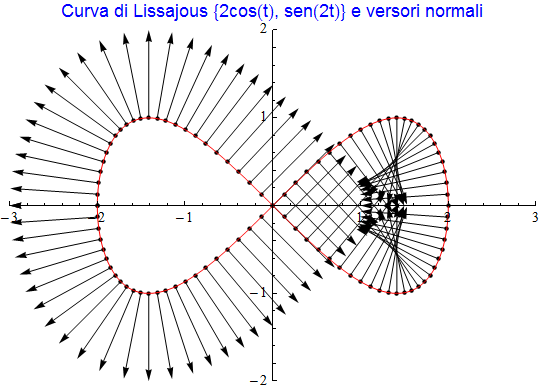
figura 11
figura 12
Continua nella seconda parte.
