Curve e curvature: terza parte

Curve e curve piane: un'introduzione ad alcune proprietà locali delle curve piane

di Lorenzo Roi

Generalizzazione

1. Definizione di curvatura
2. Esempi e segno della curvatura orientata

Centro di curvatura ed evoluta

1. Centro di curvatura e segno
2. Catalogo di curve e relative evolute

 

Generalizzazione

10. Definizione di curvatura

In quest'ultima parte cercheremo di generalizzare il concetto di curvatura esplicitando la dipendenza della derivata presente a primo membro della relazione dimostrata per la circonferenza

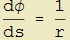
in termini delle funzioni rappresentative che descrivono la curva. A tale scopo daremo delle espressioni per i due differenziali che la costituiscono.
Sia quindi γ : {x(t),y(t)} una curva regolare descritta parametricamente. Se dt è il differenziale del parametro t, in corrispondenza di tale variazione sappiamo che i differenziali di ciascuna coordinata del punto generico P sono

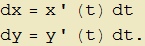(7)

Questi descrivono la variazione delle coordinate del punto P per cui il vettore ds parallelo e concorde al versore tangente e il cui modulo esprime la lunghezza dell'arco ds, si ottiene facilmente con il teorema di Pitagora (figura 22) ed è dato da

 

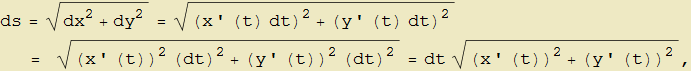
e se omettiamo la derivazione rispetto al parametro t si riscrive come

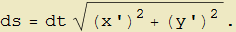(8)

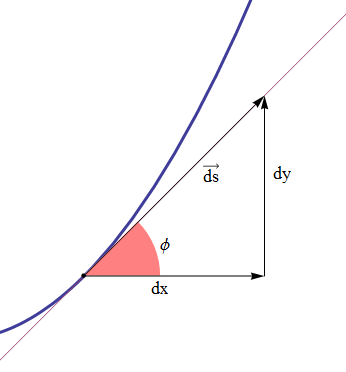
figura 22

 

Determiniamo ora l'espressione del differenziale dell'angolo che il versore tangente fa con una direzione qualsiasi per esempio quella dell'asse x di un sistema cartesiano. Questo differenziale coincide con il differenziale dell'angolo al centro della circonferenza osculatrice che, come visto, descrive pure la rotazione di tale versore. Riferendoci sempre alla figura 22 risulta che la tangente goniometrica dell'angolo φ è data da

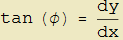
che per le espressioni (7) diviene

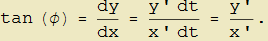
Supposto che sia x'(t) ≠ 0 deduciamo pure

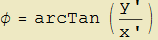
per cui non ci resta che eseguire la differenziazione

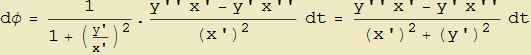
relazione che rimane valida anche indipendentemente dalla condizione x'(t) ≠ 0. Mettendo assieme quest'ultima con la (8) possiamo infine ottenere il rapporto dφ/ds come

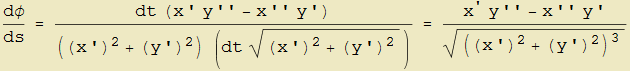
e quindi, dato che tale grandezza può essere negativa, definire la curvatura orientata di una curva γ : {x(t), y(t)} come

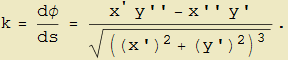(9)

Questa espressione ci permette finalmente di determinare la seconda caratteristica intrinseca di una curva piana e, cosa particolarmente importante, indipendentemente dal calcolo esplicito, spesso arduo, della derivata dell'angolo rispetto alla lunghezza d'arco.
Volendo infine salvaguardare il collegamento tra curvatura e raggio di curvatura, grandezza quest'ultima positiva, si dovrà invece considerare il valore assoluto della curvatura orientata per cui

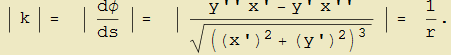(10)

11. Esempi e segno della curvatura orientata

Applichiamo l'importante risultato (9), inizialmente per confermare quanto ottenuto con approccio geometrico in precedenza per la parabola e l'ellisse. In seguito determineremo l'andamento della curvatura di alcune curve chiarendo il significato del suo segno.
La curvatura dell'ellisse ε : {a cos t, b sen t} di semiassi a  e b che si deduce dalla (9) è

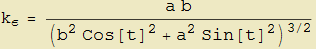
che, nel caso di a = 2 e b = 1 coincide, a meno di trasformazioni goniometriche con il risultato già trovato.

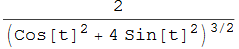
Per la parabol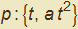a si ha

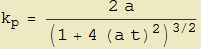
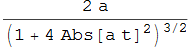
che pure coincide con il risultato già dedotto se si pone a = 1.

Funzione seno

Se parametrizziamo la funzione seno come {t, sin t} la sua curvatura assume la forma

il cui grafico è riportato nella figura 23 assieme alla funzione stessa dato che l'ascissa coincide con il parametro.

figura 23

Funzione cubica

Data la funzione cubica dispari di equazione 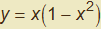parametrizzata in 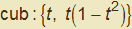la sua curvatura è

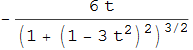
che, rappresentata assieme alla stessa cubica, mostra l'andamento di figura 24

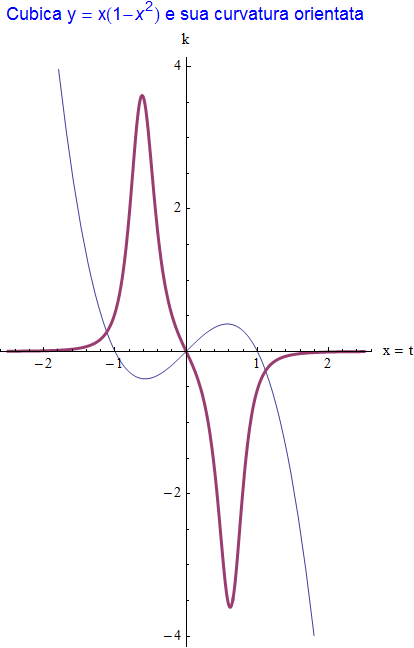
figura 24

Funzione di Lissajous

Definita la funzione di Lissajous lj : {2 cos t, sin (2t)}, della quale abbiamo già fornito il grafico nella prima parte, la sua curvatura risulta

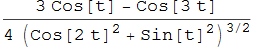
mentre il grafico (fig. 25) è

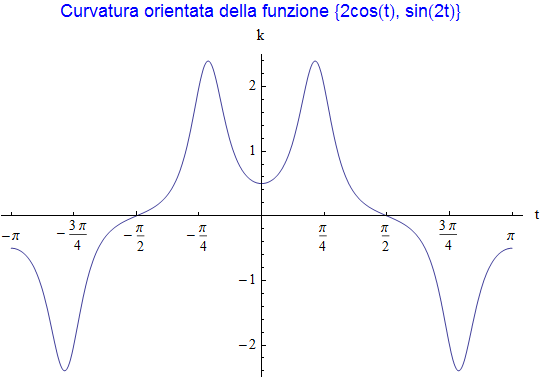
figura 25

Circonferenza

Riprendiamo infine il semplice esempio della circonferenza di raggio unitario per fornire la chiave interpretativa del segno della curvatura. Nella prima rappresentazione grafica (fig. 26a) la curva, parametrizzata come {cos t, sin t}, viene percorsa in verso antiorario e la curva piega verso sinistra rispetto alla direzione del versore tangente: nella seconda (fig. 26b) la medesima curva parametrizzata come γ : {cos(-t), sin(-t)} è percorsa in verso orario e quindi la circonferenza piega verso destra. In corrispondenza il versore tangente ruota in verso antiorario nel primo caso (e quindi la variazione dell'angolo è positiva), ruota in verso orario nel secondo. Tutto ciò si riflette sul segno della curvatura, positiva e unitaria nel primo, pari a -1 nel secondo.

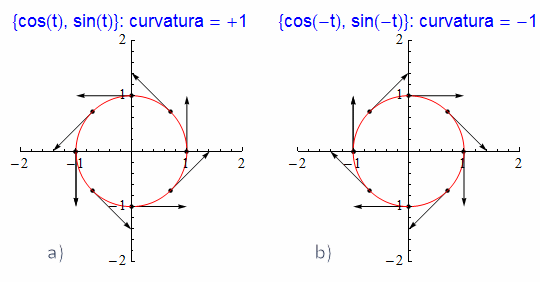
figura 26 a, b

Alla stessa conclusione si perviene osservando gli esempi precedenti del seno, della cubica o della funzione di Lissajous. Difatti, individuata la direzione del versore tangente, là dove la curva piega rispetto a questa direzione verso sinistra ossia il versore tangente tende a ruotare in verso antiorario la curvatura orientata appare di segno positivo mentre al contrario, la curvatura è negativa se la curva piega verso destra e il versore tangente ruota in verso orario.

Osservazione

La rappresentazione finora utilizzata della circonferenza con centro nell'origine è stata la seguente: γ : {r cos t, r sin t} con r misura del raggio e 0 ≤ t < 2π. Una rappresentazione parametrica alternativa meno nota è invece

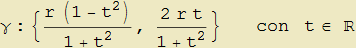
che, comunque, non comprende il punto (-r, 0). A conferma dell'indipendenza della curvatura dalla particolare parametrizzazione entrambe forniscono come curvatura il valore 1/r.

Centro di curvatura ed evoluta

12. Centro di curvatura e segno

Per completare il percorso seguito intendiamo qui dedurre le coordinate del centro di curvatura per poi rappresentarne l'andamento in corrispondenza di alcune curve. A tal fine vanno riprese due osservazioni già esposte:

• il centro di curvatura appartiene alla normale nel punto 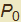di γ:
• la distanza di tale punto da 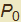è pari al raggio di curvatura.

Queste due osservazioni ci permettono di risolvere con relativa facilità il problema. Difatti data la curva γ : {x(t),y(t)}, la retta normale nel punto 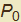corrispondente al valore 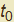del parametro è individuata non appena si abbia il versore normale. Per quanto visto tale versore è

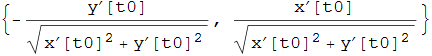
e si ottiene da quello tangente con una rotazione antioraria di 90°. La retta normale è quindi in forma parametrica

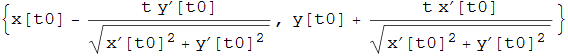
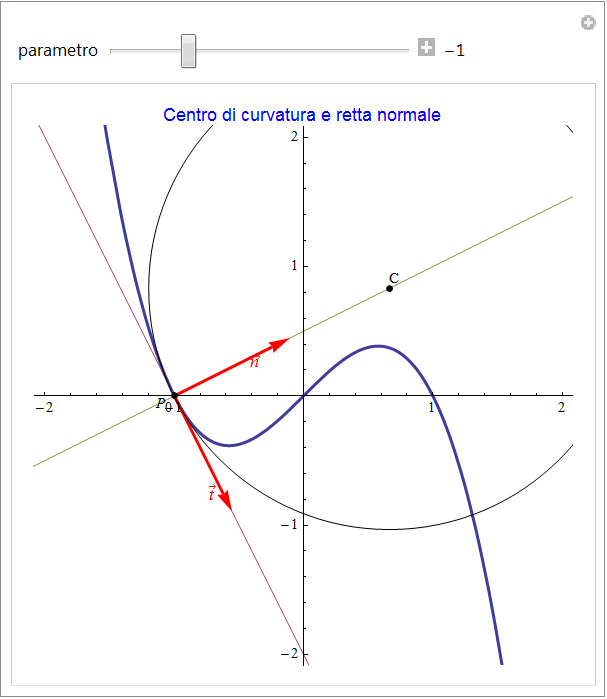
dove il parametro t esprime sostanzialmente la coordinata di un punto sulla normale a partire da 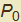considerato come origine. Pertanto se sostituiamo a t il valore con segno del raggio di curvatura 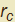potremo correttamente individuare il centro C: difatti se 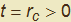il centro sarà disposto ad una distanz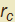a da 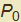concordemente al versore normale (animazione di fig. 27 con t < 0) mentre se 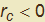apparterrà alla semiretta normale che non contiene il versore normale (fig. 27 e t > 0).

figura 27

Non ci resta che sostituire al parametro t nella retta normale il valore del raggio di curvatura nel punto 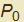ottenendo

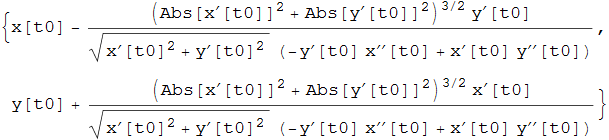
Riportando il tutto in funzione di t, otteniamo infine il luogo dei centri di curvatura

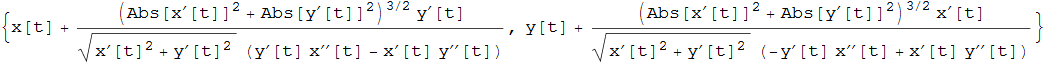
Tale luogo viene detto evoluta della curva. Siamo quindi in grado di associare ad ogni curva regolare una seconda curva, la sua evoluta. Di seguito riportiamo alcuni esempi di curve e rispettive evolute evidenziando in colore i raggi di curvatura di un opportuno numero di punti della curva.

13. Catalogo di curve e relative evolute

Di seguito e in conclusione, presentiamo un piccolo catalogo prevalentemente visuale di curve e relative evolute tracciando in colore pure un certo numero di raggi di curvatura.

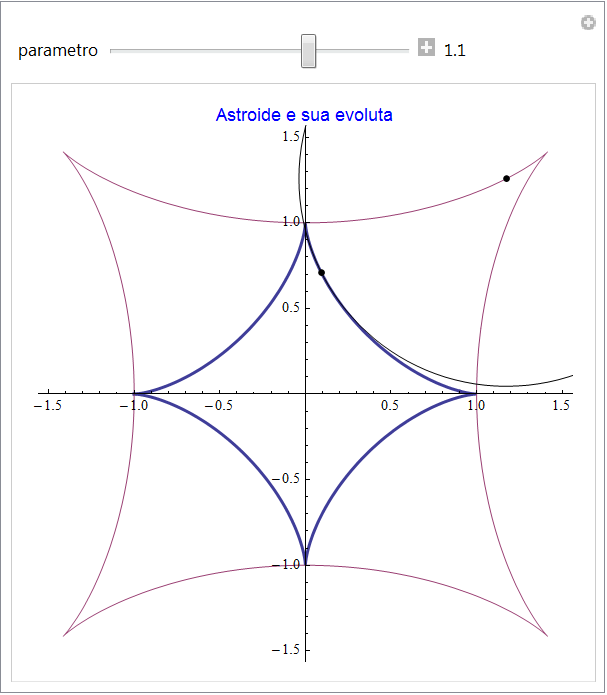
Astroide

La curva dell'astroide (detta anche asteroide) si rappresenta parametricamente tramite la coppia di funzioni 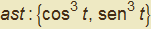. Il centro di curvatura è descritto dalla coppia di funzioni seguente e la fig. 28 ne riporta il grafico assieme a quello della curva originaria.

 

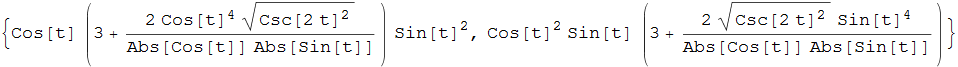
figura 28

Se in aggiunta, tracciamo anche un certo numero di rette normali la figura che emerge (fig. 29) suggerisce come l'evoluta si possa considerare anche come quella curva tangente a ciascuna retta normale ossia costituisca l'inviluppo delle rette normali.

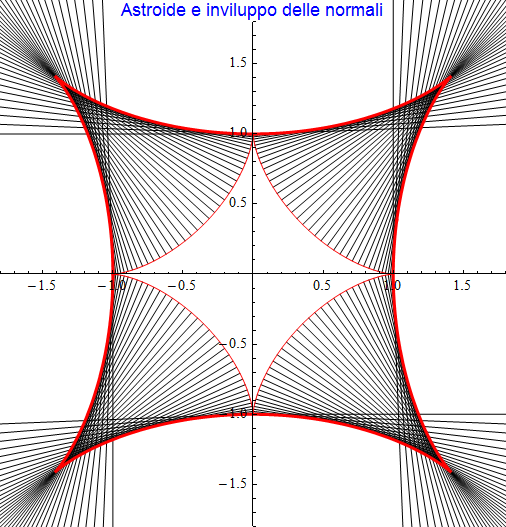
figura 29

Tracciando solo i raggi dei cerchi osculatori si ottiene una conferma grafica di ciò (fig. 30).

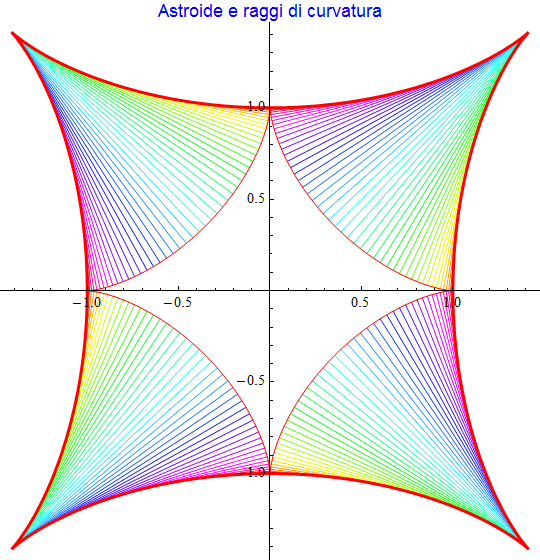
figura 30

Cardioide

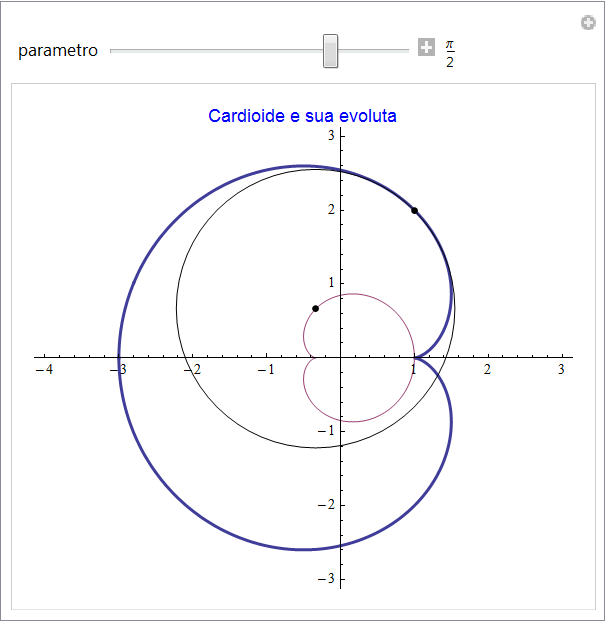
L'evoluta di una cardioide {2 cos(t) - cos(2t), 2 sin(t) - sin(2t)} è un'altra cardioide in quanto il luogo dei centri di curvatura è dato da

 

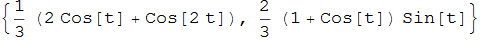
figura 31

Nella figura 32 e nella analoghe che seguono, forniamo entrambe le curve con evidenziati in colore un certo numero di raggi di curvatura.

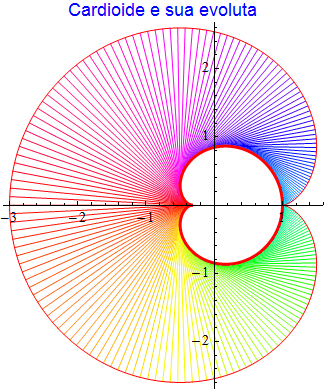
figura 32

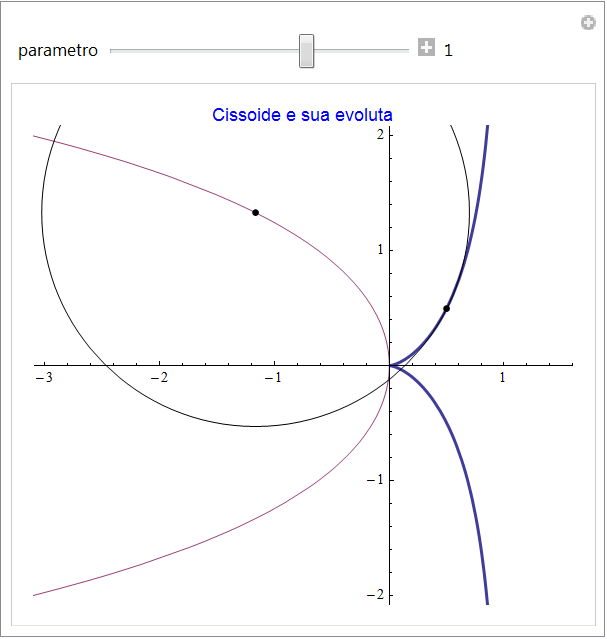
Cissoide di Diocle

Le funzioni che descrivono la cissoide di Diocle sono {t2/(1 + t2), t3/(1 + t2)} e, in corrispondenza, l'evoluta risulta

 

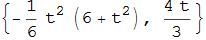
figura 33

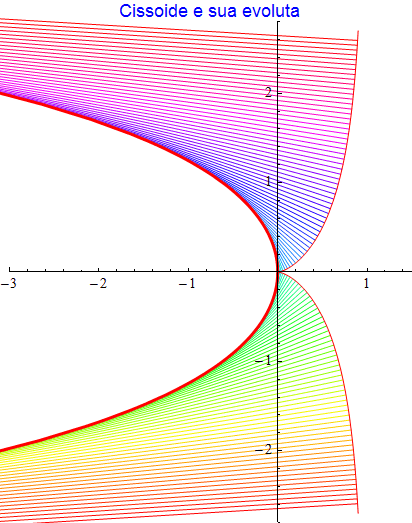
figura 34

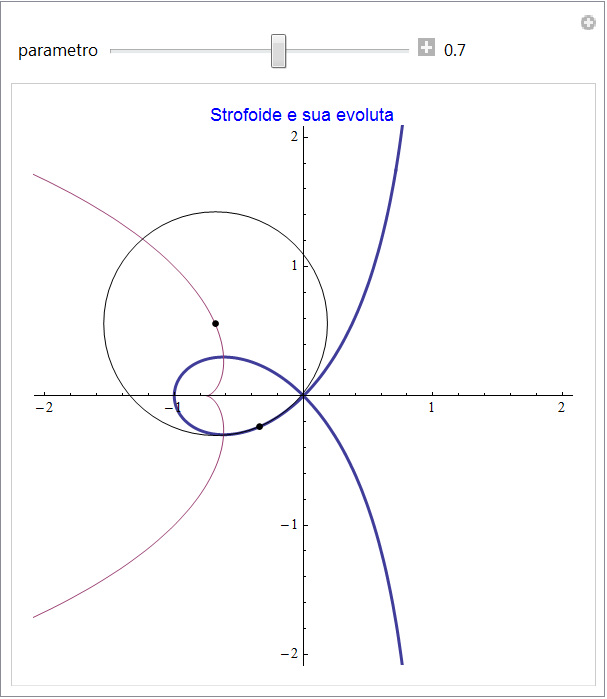
Strofoide

La strofoide è data dalla coppia {(t2 - 1)/(1 + t2), t(t2 - 1)/(1 + t2)} e in corrispondenza il luogo dei centri di curvatura risulta

 

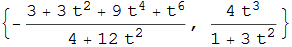
figura 35

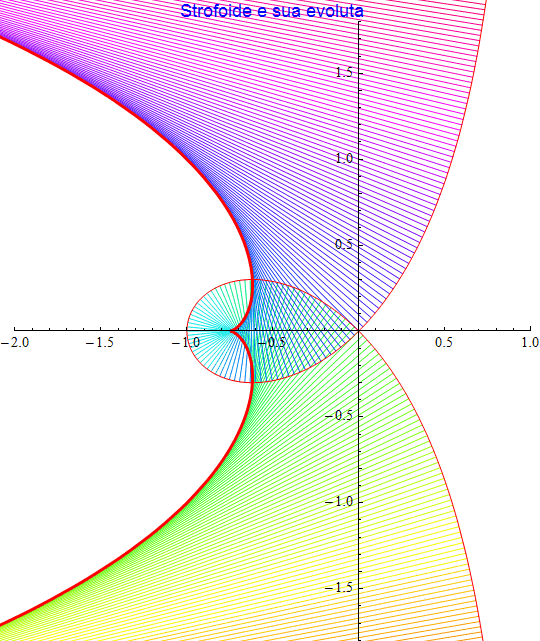
figura 36

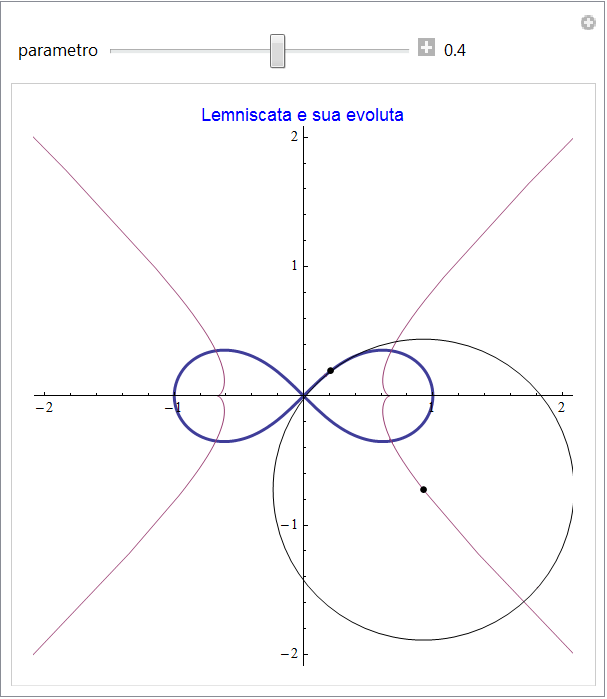
Lemniscata di Bernoulli

La lemniscata di Bernoulli è rappresentata come {sin(t)/(1 + cos2(t)), (sin(t)cos(t))/(1 + cos2(t))} mentre la sua evoluta risulta

 

figura 37

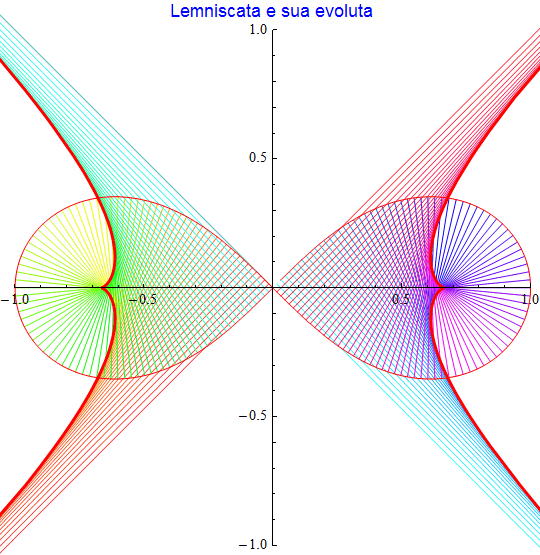
figura 38

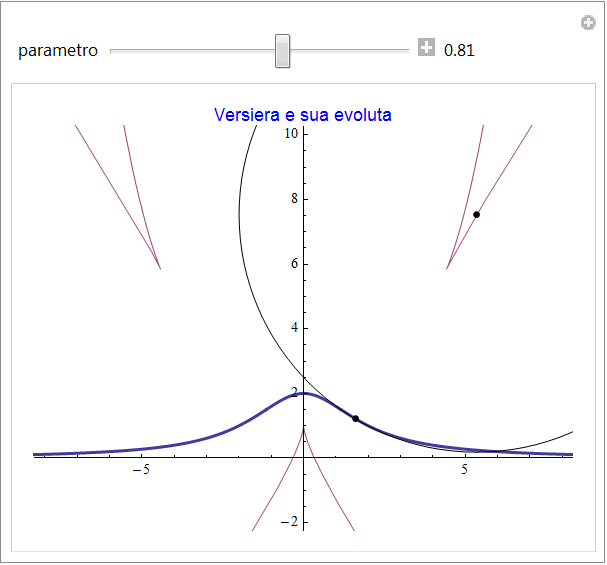
Versiera della Agnesi

La rappresentazione della curva versiera è {2 t, 2/(1 + t2)} e possiede l'evoluta

 

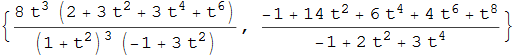
figura 39

La curvatura di tale curva mostra l'andamento di fig. 40

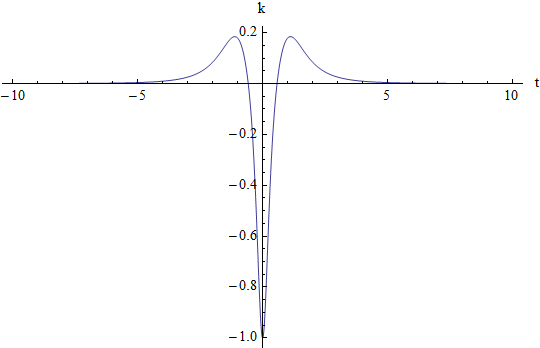
figura 40

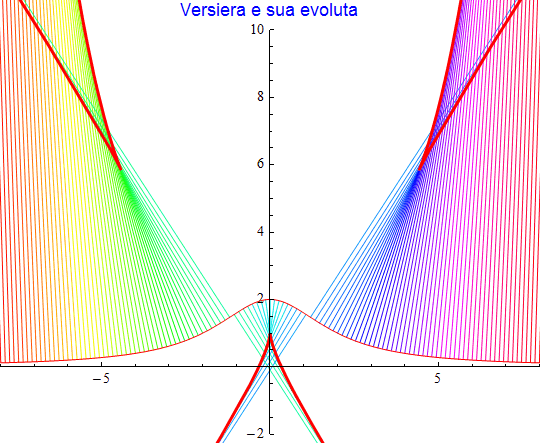
figura 41

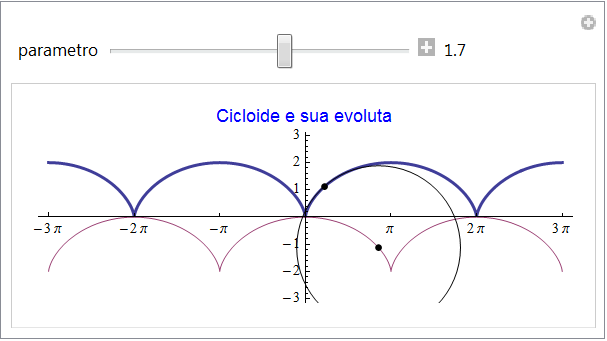
Cicloide

Come la curva cardioide anche l'evoluta di una cicloide {t - sin(t), 1 - cos(t)} è ancora una cicloide come appare dalla rappresentazione seguente.

 

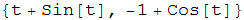
figura 42

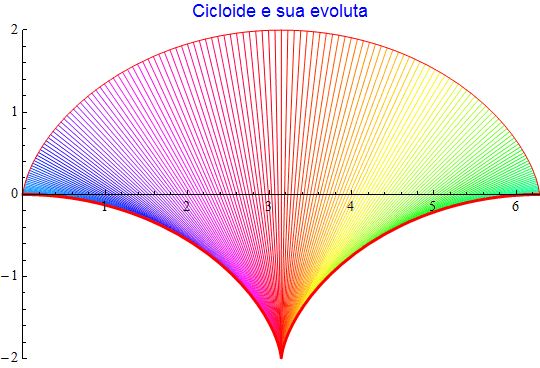
figura 43

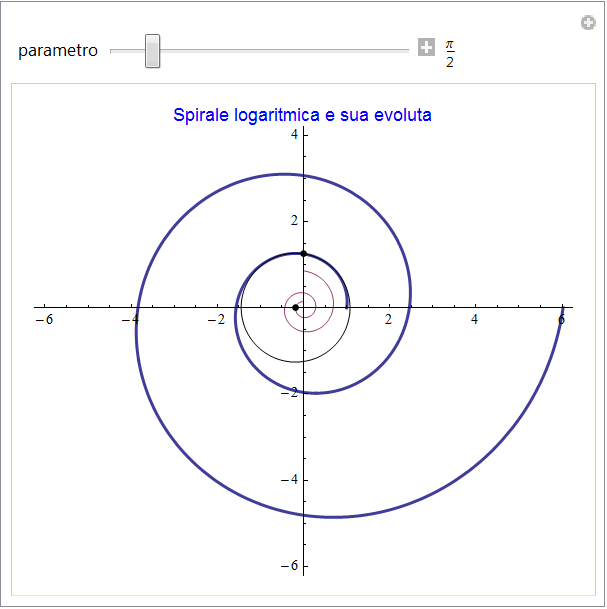
Spirale logaritmica

Anche la spirale logaritmica descritta dalle {exp(t/7) cos(t), exp(t/7) sin(t)} possiede una evoluta dello stesso tipo

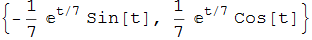
mentre la sua curvatura è sostanzialmente la funzione esponenziale

 

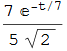
figura 44

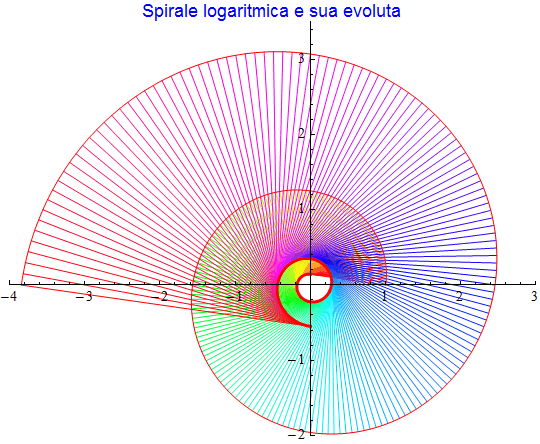
figura 45

Nella successiva immagine sono invece tracciate le circonferenze osculatrici con in evidenza nella parte centrale l'evoluta.

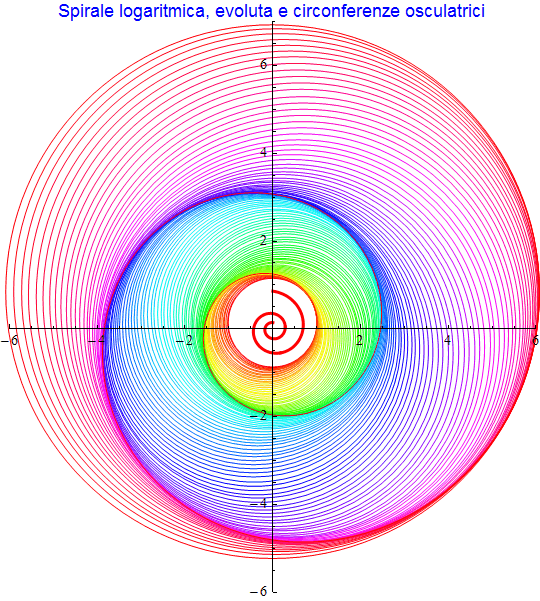
figura 46

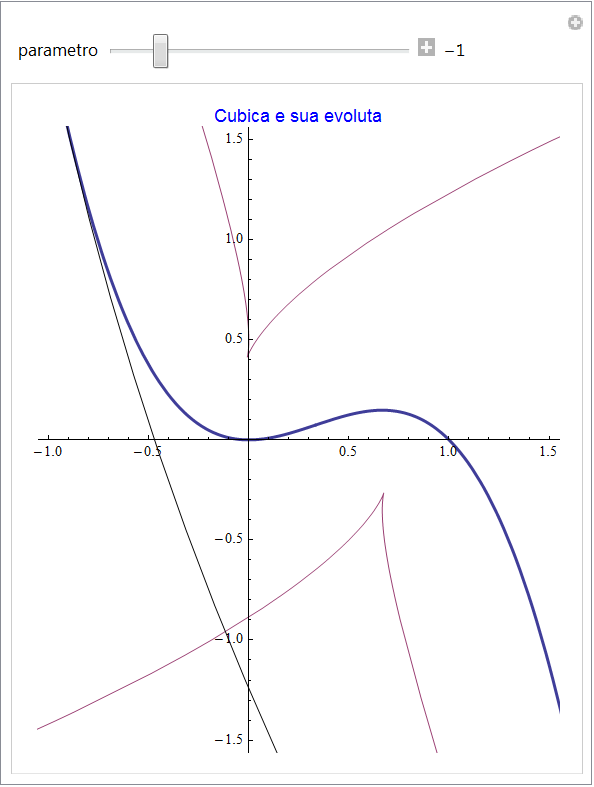
Cubica

La funzione cubica parametrizzata come {t, t2(1 - t)} possiede evoluta descritta dalla coppia di funzioni

 

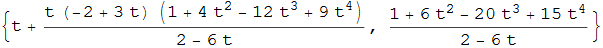
figura 47

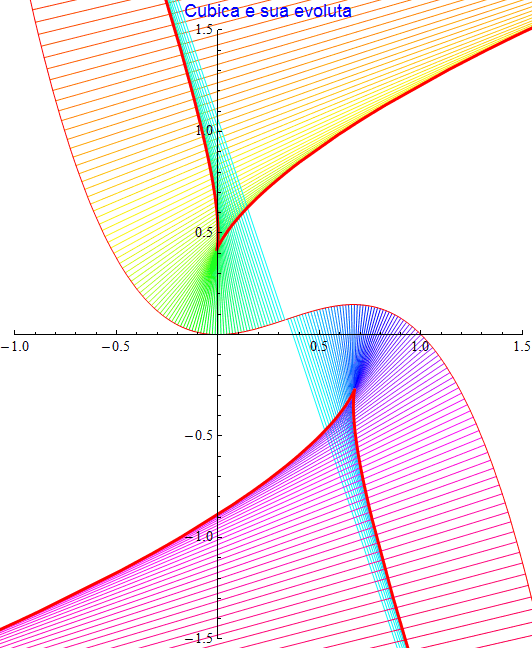
figura 48

Bibliografia

• M. Abate, F. Tovena: Curve e superfici. Springer (2008)
• E. Kreyszig: Differential Geometry. Dover (1991)
• A. Gray, E. Abbena, S. Salamon: Modern Differential Geometry of Curves and Surfaces with Mathematica. Third Edition, Chapman & Hall/CRC (2006)