Search

Giuseppe Battaglini era nato a Napoli l'11 gennaio 1826; vi è morto il 29 aprile 1894.

Studiò alla Scuola degli Ingegneri di Napoli e privatamente, anche se fu sostanzialmente un autodidatta. Fu, per breve tempo (1850), "alunno" dell’Osservatorio astronomico di Capodimonte in Napoli, da cui si dimise per non firmare una "spontanea" domanda al Re Ferdinando II di abolire la Costituzione del '48. Dopo la caduta dei Borboni, alla fine del 1860, fu nominato da Garibaldi professore di Geometria superiore nella riordinata Università di Napoli. Nel 1871 fu chiamato all'Università di Roma, dove rimase 15 anni fungendovi anche da Rettore e da Preside di Facoltà e contemporaneamente insegnando anche all'Istituto Tecnico della città. Nel 1885, già malfermo in salute, ritornò all'Università di Napoli, da dove non si mosse più. Nel 1863 fondò a Napoli il prestigioso "Giornale di Matematiche", più noto come "Giornale di Battaglini".

Fu essenzialmente un geometra, che molto contribuì, con la sua opera personale e con l'incitamento ai più giovani, a togliere l'Italia dalle sue misere condizioni scientifiche. I suoi contributi personali riguardano principalmente la teoria delle forme e la geometria della retta, in cui uno speciale tipo di complesso di 2° grado porta ora il suo nome.

Fu membro fin dal 1873 dell'Accademia dei Lineei e di molte altre accademie.

Necrologio: "Memorie Lincei", (5) 1 (1894), pp. 558-610 (E. D'Ovidio); "Giornale di Matematiche (di Battaglini)", (2) 1 (1894), pp. 205-208 (A. Capelli) e (2) 14 (1907), pp. 229-274 (F. Amodeo).

Guido Castelnuovo era nato a Venezia da Enrico, noto letterato, il 14 agosto 1865; è morto a Roma il 27 aprile 1952.

Dopo aver frequentato il Liceo “Foscarini” di Venezia (dove l'efficace insegnamento di Aureliano Faifofer contribuì ad indirizzarlo alla Matematica), si laureò a Padova nel 1886. Qui, tra gli altri, ebbe come maestro Giuseppe Veronese. Fu quindi a Roma per un breve periodo (1886-87) di perfezionamento sotto Luigi Cremona, per recarsi poi a Torino dove, dal 1887 al 1891, fu assistente di Enrico D'Ovidio e strinse amicizia con il quasi coetaneo Corrado Segre. Il periodo torinese fu determinante per il suo orientamento scientifico. Divenuto nel 1891 professore di Geometria all'Università di Roma, vi rimase per tutto il resto della sua lunga e fruttuosa carriera.

Castelnuovo fu, assieme a Corrado Segre, a Federigo Enriques (suo cognato) e a Francesco Severi, il fondatore della scuola italiana di Geometria algebrica che, per alcuni decenni, assicurò all'Italia una posizione di assoluto primato in questo settore della ricerca matematica. In particolare si debbono a Castelnuovo le condizioni necessarie e sufficienti per la razionalità delle superfici algebriche, la dimostrazione della razionalità dell'insieme delle involuzioni piane e lo studio approfondito delle superfici irregolari. L'attività di Castelnuovo nella Geometria algebrica si arresta però, salvo sporadici contributi posteriori, intorno al 1906. Nell'epoca successiva, il suo interesse fu attirato da altre questioni e principalmente dal Calcolo delle probabilità, a cui dedicò un trattato in due volumi (prima edizione 1918) che per lunghi anni fece testo in materia.

Guido Castelnuovo

Le persecuzioni razziali, scatenatesi quando era già a riposo, circondato da generale ammirazione e simpatia, non lo toccarono direttamente salvo la necessità di nascondersi per qualche mese. Dopo la liberazione di Roma nel 1944 fu nominato Commissario del CNR, di cui inizia il risanamento. Nei “vivaci” mesi di quel periodo viene però sospeso bruscamente dal suo incarico. Successivamente (1945) contribuì più efficacemente di tutti alla rinascita dell'Accademia dei Lincei (soppressa dal fascismo nel 1939) di cui fu il primo, autorevolissimo, presidente sino alla morte. Dal 1949 fu uno dei soli cinque Senatori a vita previsti dalla nuova Costituzione italiana.

L'Istituto matematico dell'Università di Roma è a lui intitolato. All'Accademia dei Lincei vi è un medaglione in suo ricordo.

Necrologio: "Accademia dei Lincei", fascicolo speciale del 1953 (G. Fano); Bollettino UMI, (3) 7 (1952), pp. 241-46 (L. Campedelli).

Opere: Memorie scelte (Bologna, Zanichelli, 1937).

Iacopo Barsotti era nato a Torino il 28 aprile 1921; è morto a Padova il 27 ottobre 1987.

Aveva studiato alla "Normale" di Pisa e si era laureato nel 1942. Assolti gli obblighi militari, era tornato a Pisa come perfezionando alla stessa Normale. Fu assistente a Roma, con Francesco Severi, dal 1946 al 1948 e poi si trasferì negli Stati Uniti: dapprima come "fellowship" a Princeton e poi come "full professor" all'Università di Pittsburgh (fino al 1960) e alla Brown University. Primo ternato in un concorso di Geometria, fu chiamato a Pisa nel 1961 come docente di Geometria e, successivamente, di Algebra. Nel 1968 si trasferì a Padova, dove insegnò Geometria fino alla morte.

Iacopo Barsotti

La sua produzione scientifica, che conta una cinquantina di lavori, comprende contributi alla teoria delle algebre, ai fondamenti della Geometria algebrica e soprattutto, nell’ambito di queste discipline, risultati fondamentali relativi alle varietà abeliane e, più generalmente, alla struttura delle varietà gruppali. Di Barsotti va ricordata anche la costruzione di gruppi analitici associati alle varietà abeliane che sono oggi noti con il nome di gruppi di Barsotti-Tate e sono all’origine della cosiddetta coomologia cristallina. Di interesse sono anche gli studi connessi alle funzioni theta, da lui generalizzate introducendo la classe di funzioni tipo-theta. Le metodologie impiegate nei suoi lavori riflettono i contatti che egli aveva avuto con l'ambiente internazionale, cui si era forse accostato per superare il disagio che gli derivava dall’isolamento in cui per un certo periodo si era trovata la Matematica italiana.

Carlo Rosati era nato a Livorno il 24 aprile 1876; è morto a Pisa il 19 agosto 1929.

Laureatosi a Pisa nel 1897, allievo della "Normale" , fu dapprima (1897-99) assistente di Ulisse Dini per l'Analisi infinitesimale. Poi, insegnò per 24 anni nelle scuole medie; da ultimo, fu professore all'Istituto tecnico di Pisa finché nel 1923, risultato secondo nella terna di vincitori al concorso di Geometria proiettiva e descrittiva dell’Università di Parma, fu nominato docente di questa disciplina all'Università di Pisa, dove rimase sino alla prematura, improvvisa morte.

Carlo Rosati è autore di una ventina di lavori prevalentemente di Geometria algebrica, fra cui prevalgono quelli dedicati alla classificazione dei corpi di funzioni abeliane.

Necrologio: “Bollettino Matematico Conti”, 8 (1929), pp. 121-128 (L. Puccianti e G. Scorza).

Gino Loria era nato a Mantova nel 1862; è morto a Genova il 30 gennaio 1954. Era fratello del noto economista Arturo.

Laureatosi nel 1883 all'Università di Torino, vi rimase tre anni come assistente di Enrico D'Ovidio. Nel 1886, a soli 24 anni, fu nominato, in seguito a concorso, professore di Algebra e Geometria analitica all'Università di Genova, dove sempre rimase.

Gino Loria

Loria fu essenzialmente un cultore di storia della Matematica, a cui dedicò un gran numero di lavori e anche di libri, ma alla quantità della sua produzione non s'accompagna sempre una qualità uniforme. Tuttavia alcuni suoi libri, specie quelli sulle curve speciali, ebbero successo e furono anche tradotti in tedesco.

Durante le persecuzioni antiebraiche, trovò efficiente rifugio nelle comunità protestanti della val Pellice.

Fu socio dell'Accademia dei Lincei e dell'Accademia di Torino.

Necrologio: Rendiconti Lincei, (8) 17 (1954), pp. 402-21 (A. Terracini); Bollettino della Unione Matematica 1taliana, (3) 9 (1954), pp. 115-118 (E . Togliatti ).

Vittoria Notari Cuzzer era nata a Reggio Emilia il 17 aprile 1894; è morta a Roma il 18 luglio 1976.

Terza di otto fratelli, deve il suo nome ad un evento curioso: il giorno della sua nascita transitava per Reggio il treno speciale dell'allora Regina Vittoria d'Inghilterra.
Per volere della famiglia, frequentò la Scuola Normale (oggi Istituto Magistrale) e, ottenuto il relativo diploma, insegnò nella scuola elementare di Barco (RE) dal '14 al '16. Lasciò l'insegnamento elementare perché, appassionatasi agli studi di Matematica e conseguita privatamente la maturità tecnica, si iscrisse al corso laurea in Matematica presso l'Università di Bologna mantenendosi agli studi con lezioni private.

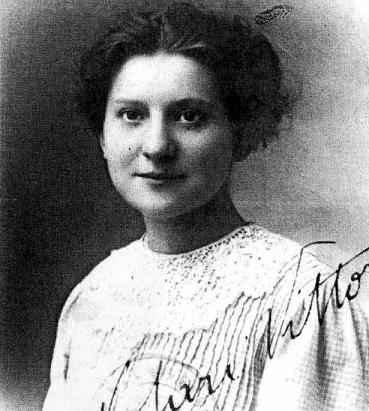
Vittoria Notari Cuzzer

Appena laureata con il massimo dei voti e la lode, avendo come relatore Federigo Enriques, nel 1920-21 ne divenne assistente volontario. In seguito, fu assistente di ruolo di Beppo Levi a Parma e di Guido Castelnuovo, Federigo Enriques e Ugo Amaldi a Roma. Nel 1933, ritenendo incompatibile gli oneri familiari con i doveri accademici, passò all'insegnamento medio e per lungo tempo insegnò Matematica e Fisica presso il Liceo classico “T. Tasso” di Roma.

La sua produzione scientifica, continuata fino a tarda età, si è svolta – sotto la guida di Enriques – nell'ambito della Geometria algebrica e della didattica della Matematica, con una collaborazione attiva alla Serie quarta (quella iniziata da Enriques nel 1922) del Periodico di Matematiche.

Ugo Amaldi era nato a Verona il 18 aprile 1875; è morto a Roma l'11 novembre 1957.

Nel 1898 si laureò in Matematica a Bologna, ove subì specialmente l'influenza di Salvatore Pincherle. Poco dopo (1903) fu nominato professore di Algebra e Geometria analitica a Cagliari, ove rimase due anni. Passò poi all'Università di Modena (1906-1919), a quella di Padova (1919-24) e quindi a Roma, ove insegnò prima nella Facoltà di Architettura (1924-42) e poi in quella di Scienze (1942-44).

Ugo Amaldi

I suoi principali contributi scientifici concernono la Teoria dei gruppi continui di trasformazioni, cui dedicò, fra l'altro, due poderose Memorie (1912-13 e 1918) e un bel volume di Lezioni (Roma, 1942-44). Fu trattatista valente e molto apprezzato e validissimo collaboratore di Tullio Levi-Civita e Federigo Enriques, contribuendo così a creare opere che, senza di lui, o non sarebbero forse state pubblicate o lo sarebbero state in forma meno brillante.

Fu socio dell'Accademia dei Lincei e di altre, da tutti apprezzato anche per l'animo buono, giusto e sereno; fu uomo di sincera, mai ostentata, religiosità.

Necrologio: "Bollettino UMI", (3) 12 (1957), pp. 726-730, a cura di T. Viola; "Atti Accademia Scienze Torino", 92 (1957-58), pp. 687-695, a cura di A. Terracini.

Cesare Arzelà era nato a S. Stefano di Magra (La Spezia) il 6 marzo 1847, qui vi è morto il 15 marzo 1912.

Fu allievo della  "Normale" di Pisa dove si laureò nel 1869. Dopo alcuni anni d'insegnamento medio, nel 1878 ottenne la cattedra di Algebra nell'Università di Palermo da dove, due anni dopo, passò per concorso alla cattedra di Calcolo all'Università di Bologna, che conservò sino alla morte.

ritratto di Cesare Arzelà

I suoi principali contributi riguardano la teoria delle funzioni di variabile reale e, più specificamente, le successioni di funzioni di una variabile da lui inquadrate nella teoria delle funzioni di due variabili reali. In particolare, determinò la condizione necessaria e sufficiente per la continuità della somma di una serie di funzioni continue e il criterio di "uguale continuità" che porta il suo nome. Si occupò pure del principio di Dirichlet, spianando la via alla celebre giustificazione data da Hilbert.

Socio corrispondente dell'Accademia Nazionale dei Lincei e di varie altre Accademie, nel 1907 condivise con Guido Castelnuovo il Premio Reale dei Lincei.

Necrologio: "Rendiconti Lincei", (5) 21 (1912), pp. 879-884, a cura di G. Lauricella; "Bollettino UMI", 9 (1930), pp. 116-l17, a cura di C. Severini.