Search
Padova Ernesto

Ernesto Padova era nato a Livorno il 17 febbraio 1845; è morto a Padova il 9 marzo 1896.
Si era laureato a Pisa nel 1866 da allievo della "Normale". Insegnò dapprima in un Liceo di Napoli, per poi essere nominato, nel 1872, su suggerimento di Enrico Betti, professore di Meccanica razionale all'Università di Pisa da dove, nel 1882, passò a Padova. Qui rimase sino alla prematura scomparsa.

Ernesto Padova
Enrico Padova è autore di una cinquantina di lavori di Analisi, Meccanica razionale e Fisica matematica (elasticità, elettro-magnetismo ecc.). In Meccanica analitica, fu tra i primi a trattare questioni di stabilità del movimento.
Fu socio dell'Accademia dei Lincei.
Necrologio: Rendiconto Lincei, (5) 51 (1896), pp. 284-285 (E. Beltrami).
Pastori Maria

Maria Pastori era nata a Milano il 10 marzo 1895; vi è morta il 17 aprile 1975.
Maestra di ruolo nelle scuole elementari dal 1915, aveva vintp il concorso per la “Normale” di Pisa e si iscrisse in quella Università dove, nel 1920, conseguì la laurea in Matematica con il massimo dei voti. Fino al 1927 insegna nelle scuole secondarie e, con l'anno accademico 1925-'26, ottiene il comando quale assistente all'Università di Milano. Qui, nel 1929 - lasciato l'insegnamento medio - diviene assistente di ruolo di Analisi e poi (1934) di Meccanica razionale. Conseguita la libera docenza in Analisi vettoriale e tensoriale nel 1931, ottiene pure l'incarico di Istituzioni di matematiche (per gli allievi di Chimica e di Scienze naturali). Nel 1939 vince il concorso di Meccanica razionale a Messina, da dove rientra quasi subito a Milano sulla cattedra di Istituzioni di matematiche per passare infine (1947) alla cattedra di Meccanica razionale, che terrà fino alla fine della carriera (1965).

Maria Pastori
La sua attività scientifica, dopo l'iniziale contatto con Gian Antonio Maggi e Umberto Cisotti, si sviluppò soprattutto nella lunga, feconda collaborazione con l'amato maestro Bruno Finzi. Grande esperta di Calcolo tensoriale e di Geometria differenziale, la sua produzione scientifica riguarda anche la meccanica dei corpi deformabili continui (elastici, elastoplastici e fluidi), la teoria della propagazione ondosa, l'elettromagnetismo, la teoria della Relatività e la Meccanica analitica.
Fu socio corrispondente dell'Accademia dei Lincei (1964) e dell'Accademia delle Scienze di Torino. Nel 1966 ebbe il premio internazionale “Isabella d'Este” per le Scienze e, all'atto del suo collocamento fuori ruolo, le fu conferita la medaglia d'oro dei “Benemeriti della scuola e della cultura”.
Necrologio: Bollettino UMI, (5), vol. XIII-A (1976), n. 1, pp. 215-216 (D. Graffi); Celebrazioni lincee, n. 95, 1976 (C. Agostinelli); Rendiconti Ist. Lombardo, vol. 110 (1976), pp. 1-8 (P. Udeschini).
Tonelli Leonida

Leonida Tonelli era nato a Gallipoli (Lecce) da famiglia veneta il 19 aprile 1885; è morto a Pisa il 12 marzo 1946.
Studiò all'Università di Bologna avendo come maestri, fra gli altri, Cesare Arzelà e Salvatore Pincherle e vi si laureò nel 1907. Nel 1913 fu nominato professore di Analisi algebrica all'Università di Cagliari dove rimase un anno. Nel 1914 passò, per concorso, alla cattedra di Analisi infinitesimale all'Università di Parma che tenne fino al 1922 salvo la parentesi della guerra a cui partecipò volontariamente. Nel 1922 fu chiamato all'Università di Bologna; nel 1930 passò a Pisa, su invito di Giovanni Gentile che gli promise condizioni molto favorevoli nella fondata speranza che egli potesse, come effettivamente avvenne, risollevare le sorti di quella scuola matematica che, per alcuni anni, era stata la prima in Italia. E a Pisa egli restò, di fatto, sino alla morte, nonostante un trasferimento all'Università di Roma nel 1939-42, che restò sostanzialmente solo nominale. A Pisa Tonelli diede, fra l'altro, nuovo lustro agli Annali della Scuola Normale Superiore e formò vari, valorosi allievi. È sepolto, accanto a Ulisse Dini e a Luigi Bianchi, nel famoso Cimitero Monumentale della città.

Leonida Tonelli
Tonelli fu uno dei maggiori analisti italiani di questo secolo. Ha impresso la sua orma soprattutto nel Calcolo delle variazioni, con un utilizzo assai sofisticato dei cosiddetti "metodi diretti". I funzionali che in esso compaiono, nel cosiddetto "problema più semplice del Calcolo delle variazioni", pur non essendo in generale continui, sono però quasi sempre semicontinui e questo basta per assicurare l'esistenza del loro minimo o del loro massimo. Altri suoi importantissimi lavori riguardano le serie trigonometriche, specie quelle doppie, cui dedicò un grosso trattato. Si interessò molto di Analisi reale: è degli anni immediatamente successivi alla laurea il classico teorema (noto come "teorema di Fubini-Tonelli") relativo al calcolo di un integrale doppio mediate due successivi integrali semplici, seguito da poderosi studi altri studi sulla moderna Teoria dell'integrazione e della quadratura delle superfici in forma cartesiana.
Fu socio dell'Accademia dei Lincei - che nel 1927 gli aveva conferito il Premio Reale per la Matematica - e di varie altre Accademie, fra cui la Pontificia.
Necrologio: “Rend. Lincei”, (8) 4 (1948), pp. 594-619 (G. Sansone); “Riv. Univ. Parma”, 1 (1950), pp. 157-188 (A. Mambriani); «In Memoriam», vol. commem. a cura dell'Univ. di Pisa (1958).
Chisini Oscar

Oscar Chisini era nato a Bergamo il 14 marzo 1889; è morto a Milano il 10 aprile 1967.
Compiuti gli studi medi e universitari a Bologna, si laureò nel 1912 sotto la direzione di Federigo Enriques, del quale divenne subito assistente. Durante la prima guerra mondiale prestò servizi militare quale ufficiale dell'artiglieria alpina dando contributi ancor oggi ricordati (la costruzione di un telemetro logaritmico e la determinazione della quota degli aerei in volo mediante una proiezione bicentrale). Conseguita la libera docenza nel 1918, ebbe vari incarichi d'insegnamento nelle Università di Bologna e Modena e nel 1923 vinse il concorso per la cattedra di Geometria dell'Università di Cagliari, passando poi (1925) a quella di Algebra e Geometria analitica. Nello stesso anno fu invitato a trasferirsi a Torino e a Milano, preferì quest'ultima sede ricoprendo inizialmente la cattedra di Analisi algebrica e poi quella di Geometria che tenne fino al collocamento fuori ruolo nel 1959. A Milano fu anche incaricato di Geometria superiore all'Università e di Geometria analitica al Politecnico. Collocato a riposo nel 1964, fu nominato professore emerito di Geometria nel 1965.

Oscar Chisini
La sua principale attività di ricerca è stata rivolta alla Geometria algebrica, settore in cui esordì collaborando con Enriques alla stesura del noto trattato "Lezioni sulla teoria geometrica delle equazioni e delle funzioni algebriche", che uscì in 4 volumi tra il 1915 ed il 1934. Molte sue ricerche in questo settore sono poi legate allo studio delle singolarità di una superficie algebrica, studio condotto soprattutto avendo presente l'esigenza di costruire modelli o privi di singolarità o dotati di singolarità semplici. In quest'ambito introdusse – a semplificare la rappresentazione di una superficie algebrica sopra un piano multiplo – la cosiddetta "treccia caratteristica" (o fascio caratteristico) d'una curva algebrica piana e studiò le curve di diramazione dei piani multipli. Coinvolti dai comuni interessi con Federigo Enriques, si dedicò anche alla divulgazione del pensiero matematico (si vedano per esempio le numerose voci da lui scritte per l'Enciclopedia Italiana) e alle questioni didattiche. In quest'ultimo settore svolse un ruolo a lungo importante, anche perché Enriques lo aveva voluto segretario di redazione del Periodico di Matematiche, nella sua forma rinnovata iniziata nel 1921. Della stessa rivista Chisini fu poi direttore dal 1946 al 1967.
Socio dell'Accademia dei Lincei e di numerose Accademie locali, fu anche preside della Facoltà di Scienze tra il 1945 ed il 1950. In occasione del suo 70-esimo compleanno gli fu dedicato il 30° volume dei Rendiconti del Seminario matematico di Milano e dopo la sua morte il Periodico di Matematiche ne ha onorato la memoria pubblicando un volume speciale [(4) 46, fasc. 1-2, 1968] con saggi di diversi allievi.
Necrologio: Accademia Nazionale dei Lincei, "Celebrazioni Lincee", n. 26, 1969 (E.G. Togliatti).
Arzelà Cesare

Cesare Arzelà era nato a S. Stefano di Magra (La Spezia) il 6 marzo 1847, qui vi è morto il 15 marzo 1912.
Fu allievo della "Normale" di Pisa dove si laureò nel 1869. Dopo alcuni anni d'insegnamento medio, nel 1878 ottenne la cattedra di Algebra nell'Università di Palermo da dove, due anni dopo, passò per concorso alla cattedra di Calcolo all'Università di Bologna, che conservò sino alla morte.

ritratto di Cesare Arzelà
I suoi principali contributi riguardano la teoria delle funzioni di variabile reale e, più specificamente, le successioni di funzioni di una variabile da lui inquadrate nella teoria delle funzioni di due variabili reali. In particolare, determinò la condizione necessaria e sufficiente per la continuità della somma di una serie di funzioni continue e il criterio di "uguale continuità" che porta il suo nome. Si occupò pure del principio di Dirichlet, spianando la via alla celebre giustificazione data da Hilbert.
Socio corrispondente dell'Accademia Nazionale dei Lincei e di varie altre Accademie, nel 1907 condivise con Guido Castelnuovo il Premio Reale dei Lincei.
Necrologio: "Rendiconti Lincei", (5) 21 (1912), pp. 879-884, a cura di G. Lauricella; "Bollettino UMI", 9 (1930), pp. 116-l17, a cura di C. Severini.
Mineo Corradino

Corradino Mineo era nato a Palermo il 26 luglio 1875; vi è morto il 16 marzo 1960.
Si era laureato nella sua città natale nel 1900 e subito dopo divenne assistente di Geodesia sotto la guida di Adolfo Venturi. Nel 1922 succedette al suo maestro come incaricato e poi, in seguito a concorso, come titolare di Geodesia. Nel 1948 passò (quale professore fuori ruolo) all'insegnamento di Astronomia ma già prima, a partire dagli anni Trenta, era stato incaricato della direzione dell'Osservatorio astronomico di Palermo.

Corradino Mineo
Lascia un centinaio di pubblicazioni, principalmente di Geodesia e di Astronomia, fra cui prevalgono quelle relative alla determinazione del geoide in base a sole misure di gravità e questioni connesse.
Fu socio dell'Accademia dei Lincei e preside della Facoltà di scienze di Palermo.
Colonnetti Gustavo

Gustavo Colonnetti era nato a Torino l'8 novembre 1886; vi è morto il 20 marzo 1968.
Si era laureato in Ingegneria civile nel 1908 e nello stesso anno era stato nominato assistente di Scienza delle costruzioni. L'11 luglio 1911 si laureò anche in Matematica, nella stessa seduta in cui ottenne la laurea Alessandro Terracini (che accenna alla coincidenza nei suoi "Ricordi"). Il 1° dicembre di quell'anno fu nominato professore straordinario di Meccanica applicata nella "Regia Scuola Superiore Navale" di Genova e nel 1914 passò a Pisa in qualità di ordinario. Nel 1918 fu nominato Direttore della "Regia Scuola di Applicazione" di Pisa e tale rimase fino al 1920, quando si trasferì al Politecnico di Torino dove tenne la cattedra di Meccanica tecnica e successivamente di Scienza delle costruzioni. Dal 1° ottobre 1922 e fino al dicembre 1925 fu direttore del Politecnico di Torino, carica che dovette abbandonare per non iscriversi al partito fascista. Nel 1943 espatriò in Svizzera per non sottostare alla Repubblica di Salò e in Svizzera organizzò il cosiddetto "Campo Universitario Italiano", dove più di 200 studenti rifugiati ebbero assistenza morale e materiale e poterono seguire corsi di studio riconosciuti poi in Italia. Rientrato in Italia nel dicembre 1944, fu membro della Consulta e quindi deputato alla Costituente ma soprattutto fu presidente del CNR o, come allora si chiamava, "Consiglio nazionale delle Ricerche e della Ricostruzione" dal 1945 al 1956, contribuendo in maniera determinante alla sua ricostituzione e ristrutturazione.

Gustavo Colonnetti
La sua produzione scientifica si è sviluppata lungo tre filoni fondamentali: la Scienza delle costruzioni, la Teoria matematica dell'elasticità e l'Idrodinamica. Nel primo, oltre a numerose ricerche sperimentali, vanno ricordate le Note (elaborate prima della laurea in Matematica) in cui si espongono alcune costruzioni grafiche originali che vanno inquadrate nell'interesse che allora suscitava la Statica grafica. Le ricerche relative al secondo indirizzo di ricerca sono quelle più importanti e iniziano già con la sua tesi di laurea. In questo settore il primo risultato di rilievo è del 1912 ed è rappresentato dal teorema che egli chiamò "2° teorema di reciprocità" (il primo è quello di Betti) e che ora si chiama spesso "teorema di Colonnetti". Esso è collegato ai teoremi fondamentali dell'Elasticità (di Castigliano, di Menabrea e di Betti) e si dimostra con procedimenti analoghi. Sulle applicazioni e sulle possibili estensioni di questi teoremi Colonnetti è tornato più volte nelle sue ricerche, riassunte nel primo capitolo del trattato "L'équilibre des corps déformables" (Paris, Dunod, 1955) e nel IV cap. della "Memoria Elastoplasticità" (Accademia Pontificia, 1960). Ma la sua attività si è anche estesa in due campi collegati a quello prima accennato: lo studio dei fenomeni di isteresi elastica e quello delle deformazioni plastiche e della loro influenza nel proporzionamento delle travi. Per quanto riguarda il terzo dei settori di ricerca prima accennati, è bene almeno ricordare che in un gruppo di quattro Note del 1911 presentò alcuni sviluppi notevoli sul moto di liquidi perfetti, incompressibili e omogenei.
Fu socio dell'Accademia dei Lincei e di numerose altre sia italiane che straniere, fra cui l'Académie des Sciences de l'Institut de France, della quale fu socio corrispondente dal 1950.
Necrologio: "Celebrazioni Lincee", n. 20, 1969, (G. Supino).
D’Ovidio Enrico
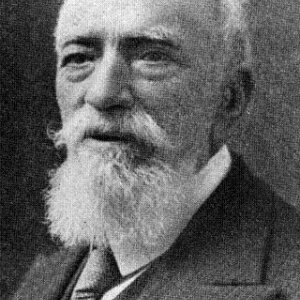
Enrico D’Ovidio era nato a Campobasso l'11 agosto 1843; è morto a Torino il 21 marzo 1933.
Studiò a Napoli nello studio privato di Achille Sannia ma ottebbe la laurea, senza esami, solo nel 1869 dopo che già insegnava da alcuni anni alla Scuola di Marina e al Liceo «Umberto». Nel 1872 ottenne, per concorso, la cattedra di Algebra e Geometria analitica all'Università di Torino, dove rimase sino al collocamento a riposo nel 1918. Per qualche tempo insegnò anche, per incarico, Geometria superiore e Analisi superiore. Fu ripetutamente preside della Facoltà, rettore dell'Università (1880-1885), direttore del Politecnico ed anche presidente dell'Accademia delle Scienze.
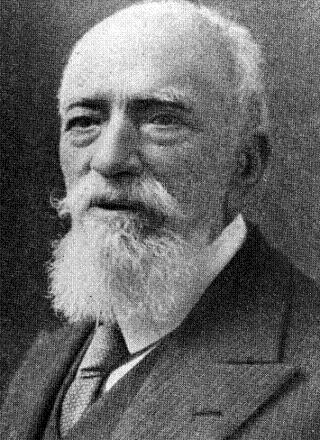
Enrico D'Ovidio
Gli si riconosce principalmente il merito di aver posto le basi su cui qualche tempo dopo, per opera prevalente di Corrado Segre che fu suo allievo, fu fondata la maggiore scuola geometrica d'Italia. I suoi contributi personali rimangono però ad un livello meno elevato e riguardano le metriche euclidee e non euclidee, le figure dello spazio rigato e soprattutto la teoria delle forme, allora molto in auge, che egli portò anche nell'insegnamento della Geometria analitica.
Nel marzo 1905 fu nominato Senatore del Regno ma correva voce (per sua natura, incontrollabile) che tale nomina fosse effetto di un equivoco e avrebbe dovuto invece riguardare il fratello Francesco (1849-1925), noto filologo, che effettivamente, pochi mesi dopo, venne fatto Senatore anche lui.
Fu socio dell'Accademia dei Lincei e di quelle di Torino, Napoli, ecc. Una via di Torino porta il suo nome.
Necrologio: “Atti Accademia Scienze Torino”, 69 (1933-34), pp. 119-127 (C. Somigliana); Annuario Univiversità di Torino pel 1932-33 (G. Fano).
Dedò Modesto

Modesto Dedò era nato a Gerenzano (Va) il 1 giugno 1914; è morto a Lugano il 23 marzo 1991.
Nel 1932 aveva iniziato gli studi in Ingegneria presso il Politecnico di Milano ma – probabilmente su consiglio di Oscar Chisini – passò poi a quelli di Matematica. Seguì i nuovi corsi fino al 1936 e preparò la tesi senza tuttavia completare gli studi. Si laureò – relatore sempre Oscar Chisini – nel 1939 e nello stesso anno vinse il concorso ad assistente ordinario di Geometria presso il Politecnico di Milano e il concorso a cattedre di Matematica e Fisica nei licei.
Richiamato al servizio militare, dopo l'armistizio del 1943 fu internato in Svizzera ove ebbe modo di organizzare vari corsi per i militari che si trovavano nella sua stessa situazione: sia di alfabetizzazione che a livello secondario e universitario presso le Università di Losanna e di Neuchatel.
Ritornato in Italia nel '45 tenne vari corsi per reduci presso il Politecnico di Milano. Negli anni dal '47 al '49 ebbe l'incarico di Geometria presso lo stesso Politecnico mentre, dal '50 al '53, tenne il medesimo corso presso l'Università. Nel 1952 divenne libero docente in "Geometria analitica con elementi di proiettiva e geometria descrittiva con disegno". Dal 1953 al 1966 fu professore di ruolo di Geometria presso l'Accademia Aeronautica di Nisida, ma nel 1966 si dimise preferendo tornare all'Università degli Studi di Milano a occuparvi – come professore aggregato – la cattedra di Matematiche complementari.
Nel 1972 vinse il concorso per professore di ruolo di Geometria e passò alla cattedra di Geometria del Politecnico. Nel 1975 si trasferì all'Università sulla cattedra di Geometria e infine nel 1979 passò a quella di Matematiche elementari dal punto di vista superiore presso la stessa facoltà di Scienze.
In tutti quegli anni accademici tenne anche corsi di Logica matematica, di Critica dei principi e di Didattica della matematica.
La sua attività scientifica si è svolta in vari settori (Geometria algebrica e Topologia nel senso classico, Geometria differenziale), ma la sua produzione è soprattutto importante nell'ambito della Didattica della matematica. È opportuno ricordare almeno i due volumi di "Matematiche Elementari dal punto di vista superiore" che riproducono il corso per la preparazione degli insegnanti che egli tenne a Napoli nel 1955-56 e i tre volumi di "Matematiche elementari".
Su mandato dell'UMI fu il coordinatore della traduzione dello School Matbematics Project (Un progetto per l'insegnamento della matematica), che la casa editrice Zanichelli pubblicò negli anni 1972-77.
Nel 1968 fu nominato membro della CIIM (Commissione per l'Insegnamento della Matematica dell’UMI), mentre dal 1973 al 1980 fu membro della Commissione Scientifica dell'UMI. Condirettore (con Carlo Felice Manara) del Periodico di Matematiche dal 1963 al 1970, fu per lunghi anni un appassionato animatore della “Mathesis” milanese, curando i rapporti fra l'Università e gli insegnanti delle scuole secondarie.
Necrologio: Carlo Felice Manara "In ricordo di un amico: Modesto Dedò" L'insegnamento della matematica e delle scienze integrate, vol.16 n.5/6 maggio/giugno 1993.